2. 机器人技术与系统国家重点实验室(哈尔滨工业大学), 哈尔滨 150080
2. State Key Laboratory of Robotics and System (Harbin Institute of Technology), Harbin 150080, China
月球探测是当前国内外星空探测的重要目标之一[1-3],载人月面探测是未来无人月面探测的必然发展趋势[4-5]. 其中,载人月球车在载人月面探测中扮演着十分重要的角色[6],是宇航员在月面执行探索任务中必不可少的工具之一[7]. 载人月球车可以搭载宇航员,到距离登月舱更远地点进行各种探测任务,扩大探索范围,提高探索行进速度[8-9];另外,载人月球车可以携带更多的月球样本和探测仪器,降低宇航员的工作强度,完成更多类型的探测任务[10]. 但是,宇航员在操纵载人月球车的同时,面对的是未知地形[11-12],工作和行驶环境的特殊性对其操纵技术提出了更高的要求. 因此,以载人月球车为主的月面活动技术是载人探月的关键技术,宇航员操纵技术的好坏关系重大,同时也要求载人月球车应具有较好的操纵性能. 月面重力是地面重力的1/6,重力的不同会引起载人月球车的动力学系统、悬架高度、垂直载荷等差异,会引起宇航员在月球和地球重力条件下驾驶载人月球车时产生操纵差异[13]. 因此,研究这种差异对驾驶员所带来的影响,不仅能够帮助宇航员在地面进行相关的驾驶训练,也可以为宇航员在月面进行探测任务提供驾驶建议. 载人月球车操纵动力学逆系统方法不需要建立驾驶员模型,在已知的载人月球车模型和运动状态的基础上,就可以反求出驾驶员对其施加的操纵输入[14]. 求解得到的宇航员操纵输入,可以用来分析什么样的操纵才是大多数宇航员驾驶载人月球车时所容易接受,同时也是行驶最安全和最快速的[15].
本文基于径向基神经网络的间接逆模型方法,建立载人月球车操纵动力学的逆系统模型. 通过得到的逆系统,对比分析宇航员驾驶载人月球车在月球和地球不同重力条件下行驶相同轨迹时所需做出的操纵输入. 最后利用Vortex仿真验证计算结果的正确性.
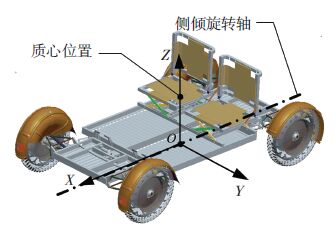
1 载人月球车操纵动力学逆系统 1.1 载人月球车操纵动力学正向模型载人月球车的三维模型如图 1所示,具有4个独立驱动的车轮,每个车轮均采用轮边电机进行驱动. 当宇航员驾驶载人月球车转向行驶时,直接控制两前轮进行转向,后两轮固定保持与车身平行的位置. 建立载人月球车的车身局部坐标系OXYZ,沿车身侧倾旋转轴前进的方向为X轴,垂直于侧倾旋转轴并过质心点向上的方向为Z轴,Y轴按照右手定则获得.
|
图 1 载人月球车三维模型及其坐标系 Figure 1 3-D model of LRV and its coordinates |
载人月球车相关的参数如下:v为载人月球车质心处行进速度,m·s-1;vf、vr为前/后轮行进速度,m·s-1;Ψ为载人月球车横摆角,rad;β为载人月球车质心的偏侧角,rad;αf、αr 为前/后轮侧偏角,rad; cαf,cαr 为前/后车轮的侧偏刚度,kN·rad-1;Kα为车轮的相对侧偏刚度,rad-1,Kα=cα/Fz;δf为前轮转向角,rad;l为轴距,m;lf、 lr为载人月球车质心距前/后轴距离,m;ρ为行驶轨迹曲线的曲率半径,m;m为载人月球车整车总质量,kg;g为重力加速度,m·s-2;JZ为绕过质心铅锤线的转动惯量,kg·m2;ms为悬架上质量,kg;J′X 为悬架上质量绕X轴的转动惯量,kg·m2;κ为载人月球车侧倾角,rad;ks为悬架等效侧倾刚度,N·m·rad-1;cs为悬架等效侧倾阻尼,N·m·s·rad-1;h为侧倾力臂,m.
将载人月球车左右侧的车轮简化到中央,利用传统地面车辆中的单轨平面模型,以质心为全局固定坐标系的原点,横坐标x0水平向右,纵坐标y0竖直向前,则车身与水平轴x0的夹角即为车身横摆角ψ,整车行驶速度方向与车身夹角即为质心处侧偏角β. 在转向运动过程中,车轮会发生侧滑现象,使前/后车轮的实际前进速度方向vf/vr与滚动方向产生一定的夹角,即为前/后轮侧偏角αf/αr,如图 2所示. 此时为了平衡整车在转向过程中产生的离心力,地面对前/后车轮会产生侧向力Fyf/Fyr.

|
图 2 载人月球车横向平移和横摆自由度 Figure 2 Lateral and yaw degrees of freedom for LRV |
载人月球车的结构形式与传统的地面车辆类似,基于操纵动力学理论,驾驶员操纵载人月球车的匀速转向过程中,主要应考虑3个自由度:绕Z轴旋转的车身横摆自由度、绕X轴的车身侧倾自由度、沿Y轴的侧向平移自由度. 基于绕Z轴的力矩平衡、绕X轴的力矩平衡、沿Y轴的力平衡,建立载人月球车3自由度操纵动力学模型,并进行化简可得
| $\left\{ {\begin{array}{*{20}{c}} {{J_Z}\ddot \psi = - gm{l_r}{l_f}{K_\alpha }\dot \psi /v + gm{l_r}{l_f}{K_\alpha }({\delta _f} + {\delta _r})/l,} \\ {{J^\prime }_X\ddot \kappa - {m_s}hv\left( {\dot \psi + \dot \beta } \right) = ({m_s}gh - {k_s})\kappa - {c_s}\dot \kappa ,} \\ {m\left( {\dot \psi + \dot \beta } \right)v - {m_s}h\ddot \kappa = - gm{K_\alpha }\beta + gm{K_\alpha }({l_r}{\delta _f} - {l_f}{\delta _r})/l.} \end{array}} \right.$ | (1) |
定义载人月球车航向角γ=β+ψ,载人月球车状态变量x(t)=ψ·ψβκ·κT,输出变量γ(t)=ψ+β,可将式(1)化为如下形式的载人月球车状态方程:
| $\left\{ {\begin{array}{*{20}{c}} {\dot x\left( t \right) = Ax\left( t \right) + B{\delta _f}\left( t \right),} \\ {\gamma \left( t \right) = Cx\left( t \right).} \end{array}} \right.$ | (2) |
定义质心行驶轨迹坐标(px,py),则其与航向角的关系可由下式表示:
| $\left\{ {\begin{array}{*{20}{c}} {{{\dot p}_x} = vcos\left( {\psi + \beta } \right),} \\ {{{\dot p}_y} = vsin\left( {\psi + \beta } \right).} \end{array}} \right.$ | (3) |
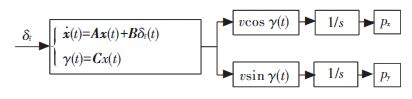
联立式(2)和(3)可求得质心轨迹坐标,但是由于式(3)的引入,给系统带来了非线性,求解框图如图 3所示.
|
图 3 载人月球车轨迹坐标求解框图 Figure 3 Solving flow diagram of trajectory for LRV |
为了便于RBF神经网络的建立,将式(1)和式(2)离散化,取常数T为采样周期间隔[16],可得
| $\left\{ \begin{gathered} X\left( {k + 1} \right) = GX\left( k \right) + H{\delta _f}\left( k \right), \hfill \\ \left[ {\begin{array}{*{20}{c}} {{p_x}\left( {k + 1} \right)} \\ {{p_y}\left( {k + 1} \right)} \end{array}} \right] = \left[ \begin{gathered} {p_x}\left( k \right) + vcos\left( {\psi \left( k \right) + \beta \left( k \right)} \right) \hfill \\ {p_x}\left( k \right) + vcos\left( {\psi \left( k \right) + \beta \left( k \right)} \right) \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered} \right..$ |
式中:G=eAT,H=(∫0TeAtdt)B.
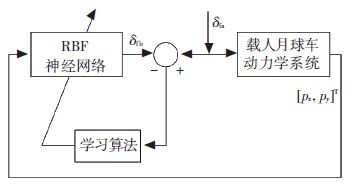
1.2 载人月球车操纵动力学逆系统模型载人月球车的逆模型建立主要有直接逆向建模和间接逆向建模两种方法[17-18]. 直接逆向建模,如图 4所示,采用输入δfa和输出[px,py]T数据,分别作为RBF网络的输入和输出来训练网络,网络权值利用载人月球车系统输入信号δfa与网络输出信号δfb的误差来修正. 但是,这种直接逆向建模存在一定缺陷,首先训练样本可能并不与所需要的训练样本相对应,存在未被训练到的控制域; 其次,如果该非线性系统的映射关系不是一一对应,可能产生一个不正确的逆模型.
|
图 4 载人月球车直接逆模型训练 Figure 4 Direct training of inverse model for LRV |
为了克服直接逆向建模的缺点,采用间接逆向模型训练方法,如图 5所示,即基于期望的载人月球车操纵动力学系统输出轨迹[pxa,pya]T与实际输出轨迹[pxb,pyb]T之间的误差来调整训练控制器权值,训练过程中,网络所接受的样本输入对应于它最终工作时接受的实际输入值.

|
图 5 间接逆模型训练 Figure 5 Indirect training of inverse model |
间接逆模型训练过程是直接指向目标的,并且可以在原系统的逆关系不是一一对应的情况下,也可以找到期望特性一个对应的逆.
2 载人月球车不同重力同轨迹行驶的求解算法基于间接逆模型,提出两种间接轨迹输入的对比方法:宇航员在地面重力条件下给出一定的操纵指令后,载人月球车行驶出一定的轨迹路线;在月面重力条件下,行驶出与上述相同的轨迹路线时,利用逆系统求解得到此时的操纵转角输入,对比两种重力条件下的操纵输入.
定义两种典型的宇航员车轮转角操纵输入:
其一为
| ${\delta _{f - e}} = 0.2sin(\pi t/4);$ | (4) |
第二种为
| ${\delta _{f - e}} = \left\{ {\begin{array}{*{20}{l}} {\pi t/90(rad),}&{t \leqslant 2.5;} \\ {(\pi /18 - \pi t/90)(rad),}&{2.5 < t \leqslant 5.0;} \\ {0,}&{t > 5.0.} \end{array}} \right.$ | (5) |
式中δf-e为载人月球车在地球重力条件下的车轮转角.
以上两种为地面实验的典型工况,一种为正弦波形的车轮转角输入,一种为斜坡脉冲的车轮转角输入. 此时式(4)和式(5)作为地球重力条件下载人月球车正向系统的输入,计算可得到相应的行驶轨迹;将此轨迹其作为图 5逆系统模型的输入,通过计算可以得到载人月球车在月面重复地面行驶出的轨迹时,所需做出的操纵转角δf-l,具体的求解过程如图 6所示.

|
图 6 月面重复地面重力条件下相同行驶轨迹的求解过程 Figure 6 Solving progress of LRV under lunar gravity repeating trajectory under earth gravity |
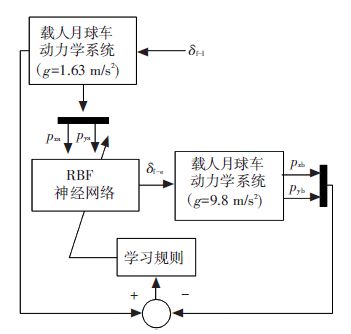
第二种间接轨迹输入的对比方法与图 6方法相类似,即:宇航员在月面重力条件下给出一定的操纵指令后,载人月球车行驶出一定的轨迹路线;在地面重力条件下,行驶出与上述相同的轨迹路线时,利用逆系统求解得到此时的操纵转角输入,对比两种重力条件下的操纵输入. 间接轨迹对比的求解过程如图 7所示.
|
图 7 地面重复月面重力条件下相同轨迹的求解过程 Figure 7 Solving progress of LRV under earth gravity repeat trajectory under lunar gravity |
阿波罗LRV的最快速度为5 m/s,本实验室设计和开发的载人月球车原理样机的理论最快速度为3.5 m/s,载人月球车最常采用的运行速度为2 m/s,因此文中仅对3个速度条件进行分析. 载人月球车动力学分析所需的参数如表 1所示.
| 表 1 载人月球车计算和仿真参数 Table 1 Parameters of calculation and simulation for LRV |
将式(4)作为图 6的输入,计算结果如图 8所示. 可以看出载人月球车在月球重力条件下,在相同的时间内,为了行驶与地球重力相同的轨迹,需要进行更大的车轮转角. 这也说明在月球重力下,宇航员需要进行更快的操纵速度. 同时,在月球重力条件下的操纵输入峰值出现时间始终超前于地球重力条件下,这说明宇航员在月球重力条件下的操纵反应时间更短.

|
图 8 月面重复地球重力条件下相同行驶轨迹时的操纵转角计算结果对比(正弦输入) Figure 8 Comparison of handling angle of LRV under lunar gravity repeating trajectory under earth gravity (sine input) |
将式(5)作为图 6的输入,计算结果如图 9所示,可以得到与图 8相类似的结论,即月球重力条件下重复行驶地球的轨迹时,需要进行更快的操纵速度,更短的操纵反应时间,以及更大的操纵幅度. 除此之外,宇航员在月面重复行驶地面相同的轨迹时,产生了更多的操纵波动,这说明宇航员在月球重力条件下需要进行多次操纵的变换来维持特定的轨迹,增大了操纵难度,也说明月球重力条件下的载人月球车的操纵稳定性较差.
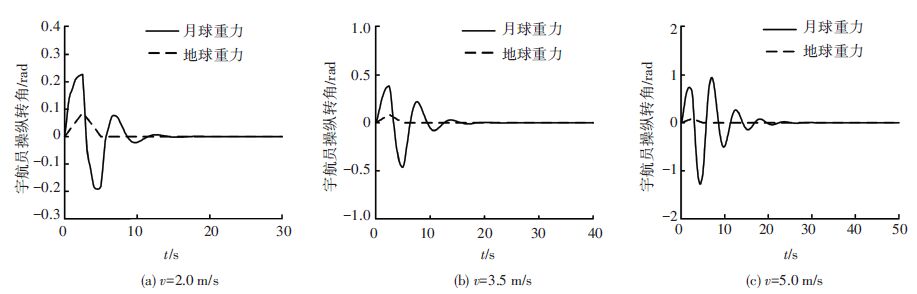
|
图 9 月面重复地球重力条件下相同行驶轨迹时的操纵转角计算结果对比(斜坡脉冲输入) Figure 9 Comparison of handling angle of LRV under lunar gravity repeating trajectory under earth gravity (pulse-ramp input) |
本文中采用Vortex软件,对载人月球车进行月球重力条件下的操纵动力学仿真,虚拟仿真模型的搭建如图 10所示. 验证方法为:将图 8和图 9中同轨迹行驶时的操纵转角计算结果,作为Vortex的载人月球车仿真模型的输入,获得相应的行驶轨迹,验证轨迹的重合程度.
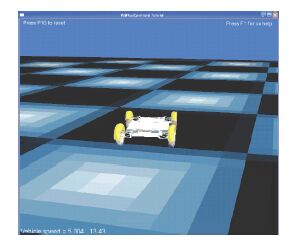
|
图 10 载人月球车虚拟仿真模型 Figure 10 Virtual simulation model of LRV |
通过Vortex的仿真,验证逆系统计算方法得到的采用图 8与图 9操纵转角的同轨迹情况,载人月球车在月球和地球重力条件下不同速度行驶时,月面重复地面同轨迹的行驶工况下,仿真轨迹几乎完全重合,验证了计算结果的精度,同时也验证了逆系统模型的正确性.
3.2 地面重复月面重力条件下同轨迹行驶的操纵动力学差异分析图 8和图 9的计算结果为月面重复地面同轨迹行驶的车轮转角操纵输入,采用的是图 6的计算方法. 为了更全面的对比不同重力条件下,宇航员操纵载人月球车行驶相同轨迹时,产生的操纵转角差异. 下面对比和分析地面重复月面同轨迹行驶时的操纵转角差异. 将式(4)和(5)的操纵转角作为图 7的输入,所得到的计算结果分别如图 11和图 12所示.

|
图 11 地面重复月球重力条件下载人月球车行驶轨迹时的车轮操纵转角计算结果对比(正弦输入) Figure 11 Comparison of handling angle of LRV under earth gravity repeating trajectory under lunar gravity (sine input) |

|
图 12 地面重复月球重力条件下载人月球车行驶轨迹时的车轮操纵转角计算结果对比(斜坡脉冲输入) Figure 12 Comparison of handling angle of LRV under earth gravity repeating trajectory under lunar gravity (pulse-ramp input) |
由图 11和图 12的计算结果,可以得到与图 8和图 9相类似的结论. 并且,宇航员在地面重力条件下重复月面上行驶出的轨迹时,所需做出的操纵转角曲线更平滑,这说明宇航员在地面条件下更容易重复或复现月面重力条件下载人月球车的行驶轨迹.
在Vortex仿真中,验证图 11、12的计算结果. 载人月球车在月球和地球重力条件下以不同速度行驶时,重复同轨迹的行驶,仿真轨迹几乎完全重合,验证了计算结果的精度,同时也验证了逆系统模型的正确性.
4 结 论1) 宇航员在“月球”重力条件下驾驶载人月球车重复“地球”重力条件下相同的行驶轨迹时,需要做出更快速的操纵速度、更大的操纵幅度、更短的操纵反应时间. 这也说明,在月球重力条件下的载人月球车操纵难度较大,操纵稳定性较差.
2) 宇航员在“地球”重力条件下驾驶载人月球车重复“月球”重力条件下相同的行驶轨迹时,其操纵转角曲线更平滑,这说明宇航员在地球重力条件下更容易重复或复现月球重力条件下月球车的行驶轨迹.
| [1] | SILK E A, CREEL R. Technology development for lunar thermal applications and the next generation of space exploration[J]. Journal of Aerospace Engineering, 2007, 221 (2) : 305-309. DOI: 10.1243/09544100JAERO170 |
| [2] | SANDERS G B, LARSON W E. Progress made in lunar in situ resource utilization under NASA’s exploration technology and development program[J]. Journal of Aerospace Engineering, 2012, 26 (1) : 5-17. DOI: 10.1061/9780784412190.050 |
| [3] | CONG P C, LAN Y F, ZHANG X. Adaptive control of dual-arm space manipulator capturing object[J]. Journal of Aerospace Engineering, 2013, 227 (6) : 992-999. DOI: 10.1177/0954410012447043 |
| [4] | VISCIO M A, VIOLA N, GARGIOLI E, et al. Conceptual design of a habitation module for a deep space exploration mission[J]. Journal of Aerospace Engineering, 2013, 227 (9) : 1389-1411. DOI: 10.1177/0954410012457292 |
| [5] | HOWE S D, O'BRIEN R C, AMBROSI R M, et al. The Mars hopper: an impulse-driven, long-range, long-lived mobile platform utilizing in situ Martian resources[J]. Journal of Aerospace Engineering, 2011, 225 (2) : 144-153. DOI: 10.1016/j.actaastro.2011.07.005 |
| [6] |
范雪兵, 邓宗全, 高海波, 等. 载人月球车金属弹性筛网轮设计与分析[J].
宇航学报, 2014, 35 (2) : 235-244.
FAN Xuebing, DENG Zongquan, GAO Haibo, et al. Design and analysis of flexible wire mesh tire for manned lunar roving vehicle[J]. Journal of Astronautics, 2014, 35 (2) : 235-244. DOI: 10.3873/j.issn.1000-1328.2014.02.016 |
| [7] | HSU H W, HORANYI M. Ballistic motion of dust particles in the Lunar Roving Vehicle dust trails[J]. American Journal of Physics, 2012, 80 (5) : 452-456. DOI: 10.1119/1.3699957 |
| [8] | LIANG Zhongchao, WANG Yongfu, CHEN Gang, et al. Mechanical model for deformable and mesh pattern wheel of lunar roving vehicle[J]. Advances in Space Research, 2015, 56 (12) : 2515-2526. DOI: 10.1016/j.asr.2015.10.019 |
| [9] | GAO Haibo, LIANG Zhongchao, DING Liang, et al. Approach for vertical loading error compensation for wheel test bench of lunar rover vehicle[J]. Journal of the Chinese Society of Mechanical Engineers, 2013, 34 (6) : 561-569. |
| [10] |
邓宗全, 范雪兵, 高海波, 等. 载人月球车移动系统综述及关键技术分析[J].
宇航学报, 2012, 33 (6) : 675-689.
DENG Zongquan, FAN Xuebing, GAO Haibo, et al. Review and key techniques for locomotive system of manned lunar rovers[J]. Journal of Astronautics, 2012, 33 (6) : 675-689. DOI: 10.3873/j.issn.1000-1328.2012.06.001 |
| [11] | DING Liang, GAO Haibo, LI Yuankai, et al. Improved explicit-form equations for estimating dynamic wheel sinkage and compaction resistance on deformable terrain[J]. Mechanism and Machine Theory, 2015, 86 (4) : 235-264. DOI: 10.1016/j.mechmachtheory.2014.12.011 |
| [12] | LIANG Zhongchao, GAO Haibo, DING Liang, et al. Analysis of driving efficiency for LRV’s wheels by forced-slip method[J]. Advances in Space Research, 2014, 54 (10) : 2122-2130. DOI: 10.1016/j.asr.2014.03.016 |
| [13] | LIANG Zhongchao, GAO Haibo, DING Liang, et al. Approach to imitate maneuvering of lunar roving vehicle under lunar gravity using a terrestrial vehicle[J]. Mechatronics, 2015, 30 (9) : 383-398. DOI: 10.1016/j.mechatronics.2015.03.004 |
| [14] |
尹浩, 赵又群, 温卫东, 等. 两种输入模型下的汽车逆问题分析[J].
哈尔滨工业大学学报, 2009, 41 (12) : 219-222.
YIN Hao, ZHAO Youqun, WEN Weidong, et al. Identification of two kinds of vehicle steering input[J]. Journal of Harbin Institute of Technology, 2009, 41 (12) : 219-222. |
| [15] |
赵又群, 尹浩, 张丽霞, 等. 汽车操纵逆动力学的现状与发展[J].
中国机械工程, 2005, 6 (1) : 77-82.
ZHAO Youqun, YIN Hao, ZHANG Lixia, et al. Present state and perspectives of vehicle handling invers dynamics[J]. China Mechanical Engineering, 2005, 6 (1) : 77-82. DOI: 10.3321/j.issn:1004-132X.2005.01.020 |
| [16] |
段广仁.
线性系统理论[M]. 哈尔滨: 哈尔滨工业大学出版社, 2006 .
DUAN Guangren. Linear system theory[M]. Harbin: Harbin Institute of Technology Press, 2006 . |
| [17] | BROOMHEAD D S, LOWE D. Multivariable functional interpolation and adaptive networks[J]. Complex Systems, 1988, 2 (3) : 321-355. |
| [18] | HAYKIN S. Neutral networks[M]. Beijing: China Machine Press, 2004 . |
 2017, Vol. 49
2017, Vol. 49


