2. 大连海洋大学 海洋与土木工程学院, 辽宁 大连 116023
2. School of Ocean and Civil Engineering,Dalian Ocean University,Dalian 116023,Liaoning,China
颗粒堆积多孔介质内流体流动的阻力特性有着重要的工程应用背景,如化工工程的填充塔的性能优化,球床气冷堆堆芯的设计与安全运行,资源工程中的石油热采,高温元件的发汗冷却等. 由于颗粒堆积多孔介质内的孔隙通道具有弯曲性和随机性特点,流体质点在其中不停地发生搀混和分离,使得内部流动阻力特性十分复杂. 多年来人们从实验和数值模拟两方面,通过简化颗粒堆积多孔介质内的孔隙结构,提出了许多阻力计算预测模型[1-6],其中应用最广泛的是Ergun型方程,方程中综合考虑了黏性项(速度的一次方项)和惯性项(速度的平方项)对阻力压降的影响.
牛顿流体Ergun型方程的具体形式为
| $\frac{{\Delta p}}{L} = {A_0} \cdot \frac{{{{\left( {1 - \varepsilon } \right)}^2}}}{{{\varepsilon ^3}}} \cdot \frac{\mu }{{d_p^2}}u + {B_0} \cdot \frac{{1 - \varepsilon }}{{{\varepsilon ^3}}} \cdot \frac{{\rho {u^2}}}{{{d_p}}}.$ | (1) |
式中:Δp/L为流体流过多孔介质的宏观压降梯度;Δp为流体流过多孔介质的阻力压降,Pa;L为通道的长度,m;ε为多孔介质的孔隙率;dp为球颗粒的直径,m;μ为流体的动力黏度,Pa·s-1;ρ为流体的密度,kg·m-3;u 为流体的表观流速(达西速度),m·s-1; A0和B0为通过实验确定的经验常数.
一般认为低雷诺数情况下,黏性项起主导作用;高雷诺数情况下,惯性项起主导作用. 但是不同研究者所得的A0和B0值并不统一,且对阻力预测流态变化区间没有形成一个统一的标准.
此外,在化工机械领域,很多流体表现出非牛顿流体的剪切特性,有必要对多孔介质中非牛顿流体的阻力压降特性进行深入的理论分析和实验研究[7-13],并给出合理的阻力计算公式. 幂律型流体是工业中常常遇到的一种非牛顿流体,其流变本构方程相对简单,所以文献研究采用的流体对象多为幂律型非牛顿流体. 典型的如Woudberg等[9] 和Smit 等[10]在求解N-S方程的基础上,采用RUC(Rectangular Unit Cell)矩形单元模型模拟了多孔介质空隙中的流体流动,并给出了纯黏幂律流体的分析模型,但求解过程十分复杂. Tang等[11] 考虑黏性力、惯性力与压力之间的力平衡关系,提出了一个预测牛顿流体和非牛顿流体流过多孔堆积床的理论模型,但模型基于简单的有序立方堆积结构,适用范围有限. Sabiri等[12]和Chhabra等[13]分别对幂律流体流过球形、非球形颗粒填充床进行了理论分析和实验研究,提出了实验模型关联式,但对非达西流区的研究不足.
作者借鉴Wu等[14]对牛顿流体在颗粒堆积多孔介质内流动机理的研究方法,在经典的Carman-Kozeny-Blake模型[15]、孔喉通道模型及平均水力半径理论[16]的基础上,尝试建立一个幂律型非牛顿流体在均匀球颗粒堆积型多孔介质中流动的阻力预测模型,得到物理意义更加明确的关于迂曲度、孔隙率、孔喉比、颗粒直径及幂律指数等参数修正的Ergun型方程表达式.
1 物理数学模型假设球形颗粒堆积多孔介质是各相同性的,其内部空隙、颗粒分布均匀,且认为流体通道由弯曲的具有一系列的突缩和突扩部分组成.
1.1 黏性项对压降的影响在流速很低时,流体流动符合经典Darcy流,流体在每个空隙内的流动近似为黏性不可压缩流体的一维定常圆管流动,此时忽略流体流动的突扩突缩效应. 而流体在通道中的横向流动则通过引入迂曲度(定义为流体实际流过的长度与流道入口与出口之间直线距离的比值,是量纲一的量)这一运动学几何标量间接反映. 幂律流体在圆管中压力流动的体积流量为
| $Q = n\pi {R^3}/\left( {3n + 1} \right){(R\Delta {P_1}/(2\mu {L_t}))^{1/n}}.$ |
式中:R为毛细管半径,n 为幂律指数,Lt为弯曲毛细管流道的实际长度.
迂曲度的定义式[15]为
| $\tau = {L_t}/L{\text{ }}.$ | (2) |
研究表明,迂曲度和颗粒的堆积排列方式有密切联系,一般认为迂曲度可表达为孔隙率的函数[17-22]. 图 1为几种迂曲度模型随孔隙率的变化关系,由图 1可知,除了孔隙率为0.5~0.6以外,各表达式的结果存在差异. 由于颗粒间实际空隙相互交叉形成复杂多变的网状结构,使迂曲度的准确描述比较困难,本文考虑到实际的堆积颗粒中有一部分是重叠遮挡的,所以采用具有代表性的Meredith等[17]给出的迂曲度表达式τ=ε-0.5. 此表达式适用绝大多数多孔结构,这一点已被广泛证明和接受.

|
图 1 迂曲度随孔隙率的变化曲线 Figure 1 Curves of the tortuosity versus porosity for different models |
对单根毛细管,其空隙通道平均速度为
| $\upsilon = \frac{Q}{{\pi {R^2}}} = \frac{n}{{3n + 1}}\cdot{R^{\frac{{1 + n}}{n}}}\cdot{(\frac{{\Delta {p_1}}}{{2\mu {L_t}}})^{1/n}},$ | (3) |
引入平均水力半径[15]
| ${R_h} = \varepsilon {d_p}/(6\left( {1 - \varepsilon } \right) + 4({d_p}/D)).$ | (4) |
式中D为堆积多孔介质的通道宽度.
按照Mehta and Hawley[23]的观点,引入边壁效应的修正系数M,且
| $M = (1 + 2{d_p}/\left( {3D\left( {1 - \varepsilon } \right)} \right)).$ | (5) |
由R=2Rh,把式(2)、(4)、(5)带入式(3)得
| $\begin{gathered} \Delta {p_1}/L = 2\mu \cdot(\left( {3n + 1} \right)/n\cdot(3\left( {1 - \varepsilon } \right)/(\varepsilon {d_p})\cdot \hfill \\ M{)^{\left( {n + 1} \right)/n}}{)^n}\cdot\tau \cdot{\upsilon ^n}. \hfill \\ \end{gathered} $ | (6) |
按照Carman[15]的观点,修正的Dupuit-Forchheimer速度关系式为
| $\upsilon = u\tau /\varepsilon .$ | (7) |
把(7)带入(6)得低流速时考虑边壁效应的幂律流体黏性项形成压降方程为
| $\begin{gathered} \Delta {p_1}/L = 6 \cdot {3^n} \cdot {\left( {\left( {3n + 1} \right)/n} \right)^n} \cdot {\tau ^{1 + n}} \cdot {M^{1 + n}} \cdot \hfill \\ {\left( {1 - \varepsilon } \right)^{n + 1}}/{\varepsilon ^{2n + 1}} \cdot \mu {u^n}/d_p^{n + 1}. \hfill \\ \end{gathered} $ | (8) |
在流动速度较高时,惯性效应必须考虑,即流体在空隙流道中流过一系列的收缩-扩张部分形成的阻力必须要考虑. 为了简化模型,假定颗粒随机堆积型多孔介质按规则菱面形排列,颗粒间距为δ.
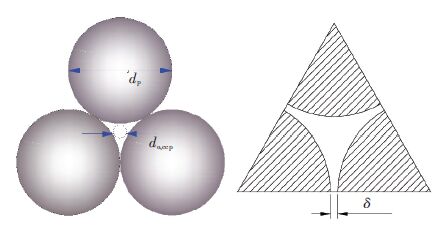
菱面形堆积颗粒体积单元如图 2所示,采用类似于Tang等[11]对有序立方堆积单元体积的简化方法,得到颗粒间距δ和喉部等效直径do,CCP分别为
| $\begin{gathered} \delta = {(^3}\sqrt {\sqrt {2\pi /6} } {/^3}\sqrt {1 - \varepsilon } - 1{\text{)}}{d_p}, \hfill \\ {d_{o,CCP}} = \frac{{4(\sqrt 3 {{({d_p} + \delta )}^2}/4 - \pi d_p^2/8)}}{{\pi {d_p}/2}}. \hfill \\ \end{gathered} $ |
为方便计算,定义水力直径dh和孔喉比λ:
| $\begin{gathered} {d_h} = 4{R_h} = 2\varepsilon {d_p}/\left( {3\left( {1 - \varepsilon } \right) \cdot M} \right), \hfill \\ \lambda = {d_{o,CCP}}/{d_h}. \hfill \\ \end{gathered} $ |
|
图 2 菱面形堆积颗粒体积单元示意 Figure 2 Schematic diagram of the volume element in rhombohedral geometry configuration |
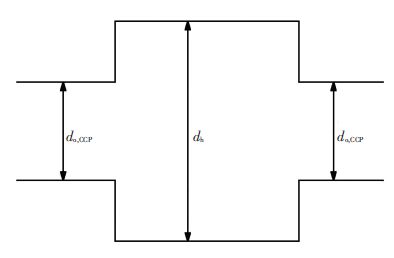
由于流体流动时发生的一系列突扩突缩效应跟流体性质无关,采用Wu等[14]类似的方法处理,如图 3所示.
|
图 3 孔喉模型示意 Figure 3 Schematic diagram of the pore-throat model |
突扩管段的压头损失为
| ${h_{fe}} = {(1 - {\lambda ^2})^2}\cdot{\upsilon ^2}/\left( {2g} \right),$ |
突缩管段的压头损失为
| ${h_{fc}} = 0.5(1 - {\lambda ^2})\cdot{\upsilon ^2}/\left( {2g} \right).$ |
所以流动惯性项形成总压头损失为
| ${h_z} = {h_{fe}} + {h_{fc}} = ({(1 - {\lambda ^2})^2} + 0.5(1 - {\lambda ^2}))\cdot{\upsilon ^2}/\left( {2g} \right).$ |
同样结合水力半径,同时考虑边壁效应的影响,幂律流体惯性项在一个孔喉管段上形成的压力降为
| $\begin{gathered} \Delta {p_2}/L = \rho g{h_z}/L \cdot {L_t}/{d_h} = \rho g{h_z}/\left( {4{R_h}} \right) \cdot \tau = \hfill \\ 0.75 \cdot [{(1 - {\lambda ^2})^2} + 0.5(1 - {\lambda ^2})] \cdot \hfill \\ {\tau ^3} \cdot M \cdot \left( {1 - \varepsilon } \right)/{\varepsilon ^3} \cdot \rho {u^2}/{d_p}. \hfill \\ \end{gathered} $ | (9) |
按照叠加原则,由式(8)、(9)得到幂律流体在堆积多孔介质内流动阻力计算模型的Ergun型方程为
| $\begin{gathered} \Delta p/L = \Delta {p_1}/L + \Delta {p_2}/L = \hfill \\ 6 \cdot {3^n} \cdot {\left( {\left( {3n + 1} \right)/n} \right)^n} \cdot {\tau ^{1 + n}} \cdot {M^{1 + n}} \cdot \hfill \\ \mu {u^n}/d_p^{n + 1} \cdot {\left( {1 - \varepsilon } \right)^{n + 1}}/{\varepsilon ^{2n + 1}} + 0.75 \cdot \hfill \\ [{(1 - {\lambda ^2})^2} + 0.5(1 - {\lambda ^2})] \cdot {\tau ^3} \cdot \hfill \\ M\left( {1 - \varepsilon } \right)/{\varepsilon ^3} \cdot \rho {u^2}/{d_p}. \hfill \\ \end{gathered} $ | (10) |
当n=1时,即简化为牛顿流体的Ergun型表达式:
| $\begin{gathered} \Delta p/L = 72 \cdot {\tau ^2} \cdot {M^2} \cdot \mu u/d_p^2 \cdot {\left( {1 - \varepsilon } \right)^2}/{\varepsilon ^3} + \hfill \\ 0.75 \cdot [{(1 - {\lambda ^2})^2} + 0.5(1 - {\lambda ^2})] \cdot \hfill \\ {\tau ^3} \cdot M \cdot \left( {1 - \varepsilon } \right)/{\varepsilon ^3} \cdot (\rho {u^2}/{d_p}). \hfill \\ \end{gathered} $ |
此时,黏性项和惯性项的两个模型系数分别为
| $\begin{gathered} {A_0} = 72 \cdot {\tau ^2} \cdot {M^2}, \hfill \\ {B_0} = 0.75 \cdot [{(1 - {\lambda ^2})^2} + 0.5(1 - {\lambda ^2})] \cdot {\tau ^3} \cdot M. \hfill \\ \end{gathered} $ |
可以看出,牛顿流体的两个系数是关于迂曲度、孔喉比(孔隙率)及边壁效应的的函数表达式,代替了Ergun公式(1)中两个经验常数,其物理意义更加明确,当M=1时,可认为不考虑边壁效应.
综上,参照式(1)的形式,对幂律型非牛顿流体的式(10),其修正的Ergun型方程可写成:
| $\frac{{\Delta p}}{L} = A \cdot \frac{{\mu {u^n}}}{{d_p^{n + 1}}} \cdot \frac{{{{\left( {1 - \varepsilon } \right)}^{n + 1}}}}{{{\varepsilon ^{2n + 1}}}} + B \cdot \frac{{\left( {1 - \varepsilon } \right)}}{{{\varepsilon ^3}}} \cdot \frac{{\rho {u^2}}}{{{d_p}}}.$ | (11) |
式中模型系数A、B的表达式如下:
| $\begin{gathered} A = 6 \cdot {3^n} \cdot {\left( {\left( {3n + 1} \right)/n} \right)^n} \cdot {\tau ^{1 + n}} \cdot {M^{1 + n}}, \hfill \\ B = 0.75 \cdot [{(1 - {\lambda ^2})^2} + 0.5(1 - {\lambda ^2})] \cdot {\tau ^3} \cdot M. \hfill \\ \end{gathered} $ |
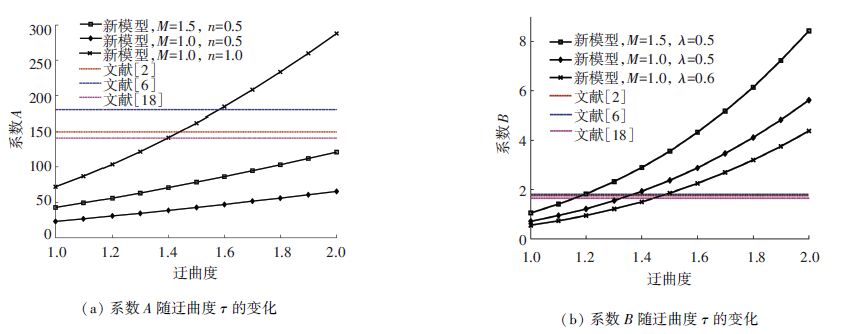
图 4为模型系数A、B随迂曲度的变化关系,并与文献中的经验系数做了对比. 如图 4(a)所示,系数A随着迂曲度的增大而增大. 特别的,对相同幂律指数(n=0.5)的流体,当考虑边壁效应时(如M=1.5),系数A的数值是增大的. 同样,系数A随着流体幂律指数的增大而增大. 当τ=1.44时,系数接近Ergun方程中经验常数150;当τ=1.58时,系数接近Mcdonald修正版Ergun方程中的经验常数180. 在图(b)中,系数B随着迂曲度的增大而增大,当考虑边壁效应时(如M=1.5),系数B的数值也是增大的,同时注意到系数B随孔喉比的增大而增大. 同样可以找出当迂曲度在某个范围内变化时,和经验常数是一致的.
|
图 4 模型系数A、B随迂曲度的变化曲线比较 Figure 4 Schematic diagram of the coefficients A and B versus tortuosity for different models |
为了验证新建模型的有效性,同时方便和文献作比较,统一把各模型按下面形式重组化简.
定义幂律流体的摩擦因子为
| ${f_p} = ( - \Delta p/L){d_p}/(\rho {u^2})({\varepsilon ^3}/\left( {1 - \varepsilon } \right)).$ | (12) |
修正的雷诺数为
| $R{e_p} = \rho {\left( {u/\varepsilon } \right)^{2 - n}}/\mu {({d_p}\varepsilon /\left( {1 - \varepsilon } \right))^n}.$ | (13) |
所以式(11)可简化为
| ${f_p} = A/R{e_p} + B.$ | (14) |
当不考虑边壁效应时,简化后的各模型中的系数见表 1.
| 表 1 各模型系数A、B的表达式 Table 1 Correlation coefficients A and B |
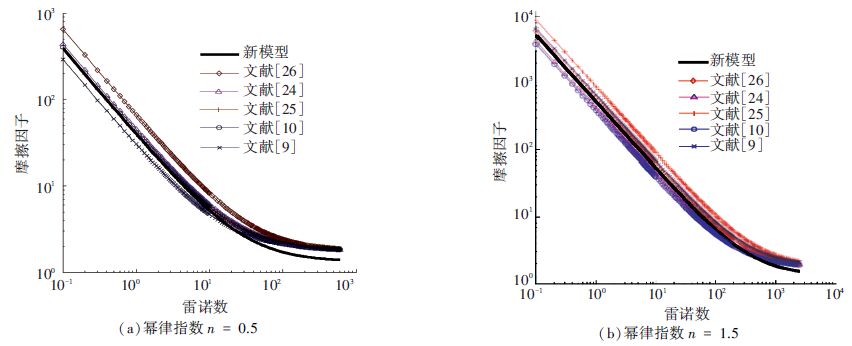
图 5是剪切变稀流体和剪切变稠流体两种流体的摩擦因子随着幂律指数的变化示意图,在堆积型多孔介质的孔隙率为0.5时,分别与文献模型关联式进行比较.
|
图 5 摩擦因子随雷诺数的变化曲线(孔隙率ε=0.5) Figure 5 Curves of friction factor versus Reynolds number for various correlations for a porosity of 0.5 |
如图 5所示,现有模型的摩擦因子预测值与文献总体上吻合较好,但是在雷诺数较大时,对于剪切变稀和剪切变稠两种流体,预测值略低. 在雷诺数较小时,摩擦因子与雷诺数近乎直线关系,且随着幂律指数的增大而增大;随着雷诺数的增大,摩擦因子与雷诺数呈非线性关系,且可以看出雷诺数很高时,摩擦因子与幂律指数无关,趋于某一定值.
2.2 实验数据比较Sabiri[12]对纯黏非牛顿流体(CMC,密度ρ为1 021 kg·m-3)通过玻璃球(球粒直径dp为2.92 mm)的堆积床的流动特性进行了实验研究,实验获得剪切应力Γ与剪切速率$\dot \gamma $的流变方程为
| $\begin{gathered} i = 1:\Gamma = 0.116\cdot{{\dot \gamma }^{0.771}},38 < \dot \gamma < 450{s^{ - 1}}, \hfill \\ i = 2:\Gamma = 0.262\cdot{{\dot \gamma }^{0.634}},400 < \dot \gamma < 3{\text{ }}500{s^{ - 1}}. \hfill \\ \end{gathered} $ |
实验数据整理后得到摩擦因子表达式为
| ${f_{exp}} = \frac{{\Delta p}}{L}\cdot\frac{{2\cdot{\varepsilon ^3}}}{{\rho {u^2}\cdot{\tau ^3}\cdot\left( {1 - \varepsilon } \right)\cdot{a_{vd}}}}.$ | (15) |
式中:多孔介质的动比面积avd=2 055 m-1;孔隙率ε=0.36,迂曲度τ=1.44. 为了便于比较,按照式(12)、(13)的定义,把式(15)写成:
| ${f_p} = A\prime /R{e_p} + B\prime .$ |
式中,实验模型系数A′、B′的表达式如下:
| $\begin{gathered} A\prime = {2^{ - n}} \cdot d_p^{n + 1} \cdot {\tau ^{1 + n}} \cdot {\left( {\left( {3n + 1} \right)/n} \right)^n} \cdot a_{cd}^{n + 1}, \hfill \\ B\prime = 0.097 \cdot {d_p} \cdot {\tau ^3} \cdot {a_{vd}}. \hfill \\ \end{gathered} $ |
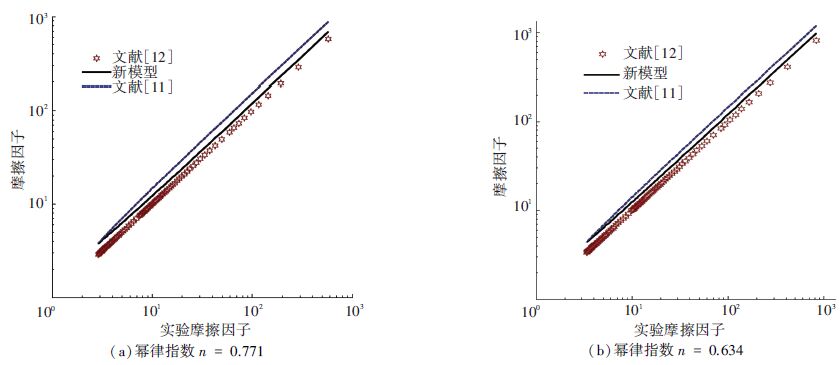
图 6为不同幂律指数(n=0.771,n=0.634)的条件下,现有模型摩擦因子的计算值与文献实验数据摩擦因子的比较. 雷诺数在一定范围变化时,与文献[11]相比,摩擦因子计算值与实验值吻合度很高;随着雷诺数的增大,二者开始出现偏差. 一方面原因是实验手段不完善,使实验数据更多地落在低雷诺数范围内,另一方面原因是随着流速的增大,模型所忽略的边壁效应和弥散效应对流动阻力的影响是逐渐增加的.
|
图 6 模型计算摩擦因子与实验摩擦因子对比曲线 Figure 6 Contrast curves of the predicted friction factor versus the experimentally friction factor |
随着流速的不断变化,黏性项引起的黏滞阻力损失所占比重和惯性项引起的动力阻力损失所占比重不断变化,幂律流体Ergun型公式中右边的第一项(黏性项)和第二项(惯性项)所占阻力压降比重分别用Xn和Xg表示:
| $\begin{gathered} {X_n} = [6\cdot{3^n}\cdot{\left( {\left( {3n + 1} \right)/n} \right)^n}{\tau ^{1 + n}}{M^{1 + n}}\mu {u^n}/{d_p}^{n + 1}\cdot(1 - \hfill \\ \varepsilon {)^{n + 1}})/{\varepsilon ^{2n + 1}}]/(\Delta p/L) = (A/R{e_p})/(A/R{e_p} + B), \hfill \\ {X_g} = \{ 0.75\cdot[{(1 - {\lambda ^2})^2} + 0.5(1 - {\lambda ^2})]{\tau ^3}M\rho {u^2}/{d_p}\cdot \hfill \\ \left( {1 - \varepsilon } \right)/{\varepsilon ^3}\} /(\Delta p/L) = B/(A/R{e_p} + B). \hfill \\ \end{gathered} $ |
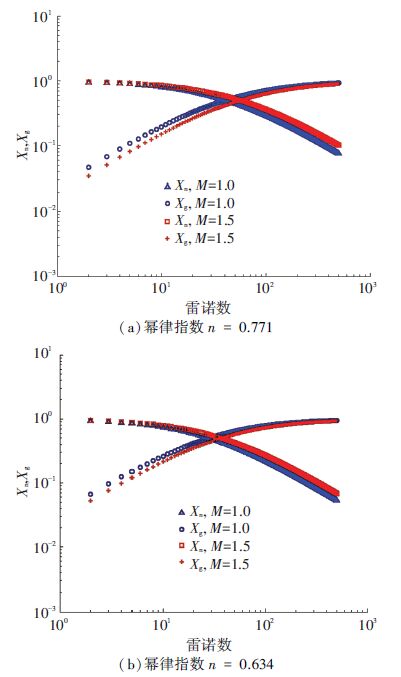
如图 7所示,在低雷诺数时,黏性项所占比重比较大,随着雷诺数的增大其比重不断减小,惯性项所占比重随着雷诺数的增大不断增大. 在雷诺数增加到某一数值时,黏性项所占比重曲线和惯性项所占比重曲线出现了交叉情况,这说明随着流速的增加,流体由以黏性项占主导作用的流动状态逐渐转变为以惯性项占主导作用的流动状态,同时说明了存在一个流态转戾的临界雷诺数. 由图 7(a)、7(b)可知,对于幂律指数n=0.771,n=0.634的情况,所对应的临界雷诺数分别为41、28时,两者所占比重相等;在相同的情况下,考虑边壁效应使临界雷诺数增大,在M=1.5时,n=0.771,n=0.634所对应的临界雷诺数分别为56、36;同时发现随着幂律指数的减小,临界雷诺数也减小.
|
图 7 黏性项和惯性项阻力压降比重随雷诺数的变化曲线 Figure 7 Curves of viscous and inertia proportion versus Reynolds number |
临界雷诺数Rec定义为达西流区和非达西流区的转戾点所对应的雷诺数值,按照式(14)可得
| $R{e_c} = \frac{A}{B} = \frac{{8\cdot{3^n}\cdot{{\left( {\left( {3n + 1} \right)/n} \right)}^n}\cdot{\tau ^{n - 2}}\cdot{M^n}}}{{[{{(1 - {\lambda ^2})}^2} + 0.5(1 - {\lambda ^2})]}}.$ |
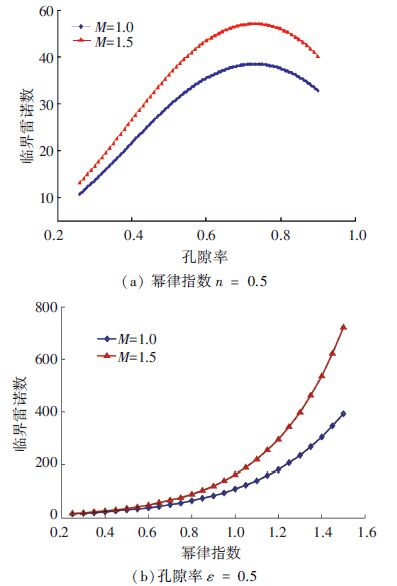
可以看出,临界雷诺数跟幂律指数n和孔隙率ε(或孔吼比λ)有着密切关系,如图 8(a)所示,随着孔隙率的增大,临界雷诺数先是逐渐增大的,可以解释为随着流体的流动空间增大,流动阻力逐渐减小,表现为黏性阻力和惯性阻力均减小,但惯性阻力减小较快,使得多孔介质中流体流态转变对应的临界雷诺数增大. 但是同时发现,当孔隙率继续增大到一定程度时(ε=0.73),临界雷诺数趋于最大值,随后随着孔隙率的增大,临界雷诺数逐渐减小,可以解释为随着流体的流动空间进一步增大,流动阻力越来越小,趋于无填充多孔介质的管道流,表现为黏性阻力和惯性阻力均减小,但黏性阻力减小更快,使得多孔介质中流体流态转变对应的临界雷诺数减小. 如图 8(b)所示,随着幂律指数的增加,临界雷诺数是逐渐增大的,因为幂律指数的增加使得黏性阻力增大较快,而惯性阻力不受影响,所以,多孔介质中流体流态转变对应的雷诺数也是增大的.
2.5 渗透率的确定基于Darcy-Forchheimer流动模型[27]的修正动量主控方程为
| $\frac{{\Delta p}}{L} = \frac{\mu }{{{K^*}}}{u^n} + \frac{{{C_F}}}{{{K^{0.5}}}}\rho {u^2}.$ |
式中: K*为幂律流体多孔介质修正渗透率,m1+n ;K为牛顿流体多孔介质渗透率,m;CF为多孔介质惯性系数.
结合式(10),则可得新建模型的渗透率和惯性系数的表达式:
| $\begin{gathered} {K^*} = \frac{{d_p^{n + 1} \cdot {\varepsilon ^{2n + 1}}}}{{6 \cdot {3^n} \cdot {{\left( {\left( {3n + 1} \right)/n} \right)}^n} \cdot {\tau ^{1 + n}} \cdot {M^{n + 1}} \cdot {{\left( {1 - \varepsilon } \right)}^{n + 1}},}} \hfill \\ K = \frac{{d_p^2 \cdot {\varepsilon ^3}}}{{72 \cdot {\tau ^2} \cdot {M^2} \cdot {{\left( {1 - \varepsilon } \right)}^2}}}, \hfill \\ {C_F} = 1/8\sqrt 2 \cdot [{(1 - {\lambda ^2})^2} + 0.5(1 - {\lambda ^2})] \cdot {\tau ^2} \cdot {\varepsilon ^{ - 3/2}}. \hfill \\ \end{gathered} $ |
|
图 8 临界雷诺数随孔隙率和幂律指数的变化曲线 Figure 8 Curves of the critical Reynolds number versus porosity and power law index |
而Tang等[11] 和Wu等[14]得到的惯性系数分别如式(16)和(17)所示:
| ${C_F} = 1/\left( {2\sqrt 2 } \right)\cdot\alpha \cdot\left( {1 - \alpha } \right)\cdot{\tau ^{0.5}}\cdot{\varepsilon ^{ - 1.5}},$ | (16) |
| ${C_F} = 1/\left( {8\sqrt 2 } \right)\cdot(1.5 + 1/{\beta ^4} - 2.5/{\beta ^2})\cdot{\tau ^{0.5}}\cdot{\varepsilon ^{ - 1.5}}.$ | (17) |
可见惯性系数在形式上是非常接近的.
由此可见,所得到的渗透率与多孔介质的颗粒直径、孔隙率、迂曲度、边壁效应系数及幂律指数密切相关;而惯性系数只是孔隙率、迂曲度、孔喉比的函数,本质上只取决于多孔介质内部的结构特征,这一观点与Hayes等[28]的结论一致.
3 结 论1) 建立了描述幂律流体在颗粒堆积多孔介质内的流动阻力计算模型,得到的修正Ergun型方程各物理量意义明确,且在一定流动范围内和已有文献数据吻合较好,模型的有效性得到证实.
2) 对黏性项和惯性项在阻力预测模型中所占比重进行了计算分析,确定了临界雷诺数的影响因素,并给出了幂律流体Darcy-Forchheimer流动动量主控方程的渗透率和惯性系数的关联式.
3) 对于幂律流体非达西流区的阻力特性研究,还需要更多实验数据的支持,仍需要通过实验进一步验证模型的正确性,并考虑边壁效应的影响,对模型进行合理修正.
| [1] | DU PLESSIS J P. Analytical quantication of coefcients in the Ergun equation for fluid friction in a packed bed[J]. Transport in Porous Media, 1994, 16 (2) : 189-207. DOI: 10.1007/BF00617551 |
| [2] | ERGUN S. Fluid flow through packed columns[J]. Chemical Engineering Progress, 1952, 48 : 89-94. |
| [3] | FAND R M, KIM B Y Y, LAM A C C, et al. Resistance to the flow of fluids through simple and complex porous media whose matrices are composed of randomly packed spheres[J]. Journal of Fluids Engineering, 1987, 109 (3) : 268-274. DOI: 10.1115/1.3242658 |
| [4] | HAYES R E, AFACAN A, BOULANGER B. An equation of motion for an incompressible Newtonian fluid in a packed bed[J]. Transport Porous Media, 1995, 18 (2) : 185-198. DOI: 10.1007/BF01064677 |
| [5] | YANG Jian, WANG Qiuwang, BU Shanshan, et al. Experimental analysis of forced convective heat transfer in structured packed beds with spherical or ellipsoilal particals[J]. Chemical Engineering Science, 2012, 71 : 126-137. DOI: 10.1016/j.ces.2011.12.005 |
| [6] | MACDONALD, I F, EL-SAYED M S, DULLIEN F A L. Flow through porous media: the Ergun equation revisited[J]. Industrial and Engineering Chemistry Fundamentals, 1979, 18 (3) : 199-208. DOI: 10.1021/i160071a001 |
| [7] | MACHAC' I, CAKLA J, COMITIB J, et al. Flow of non-Newtonian fluids through fixed beds of particles: comparison of two models[J]. Chemical Engineering and Processing, 1998, 37 (2) : 169-176. DOI: 10.1016/S0255-2701(97)00045-7 |
| [8] | CHHABRA R P. Bubbles, Drops and particles in non-Newtonian fluids[M]. Boca Raton: CRC Press, 1993 : 217 -297. |
| [9] | WOUDBERG S, DU PLESSIS J P, SMIT G J F. Non-Newtonian purely viscous flow through isotropic granular porous media[J]. Chemical Engineering Science, 2006, 61 (13) : 4299-4308. DOI: 10.1016/j.ces.2006.01.054 |
| [10] | SMIT G J F, DU PLESSIS J P. Pressure drop prediction of power law fluid through granular media[J]. Journal of Non-Newtonian Fluid Mechanics, 1997, 72 (2/3) : 319-323. |
| [11] | TANG Guihua, LU Yinbin. A resistance model for newtonian and power-law non-Newtonian fluid transport in porous media[J]. Transport Porous Media, 2014, 104 (2) : 435-449. DOI: 10.1007/s11242-014-0342-3 |
| [12] | SABIRI N E, COMITI J. Pressure drop in non-Newtonian purely viscous fluid flow through porous media[J]. Chemical Engineering Science, 1995, 50 (7) : 1193-1201. DOI: 10.1016/0009-2509(94)00495-D |
| [13] | CHHABRA R P, SRINIVAS B K. Non-Newtonian purely viscous fluid flow through packed beds: effect of particle shape[J]. Powder Technology, 1991, 67 (1) : 15-19. DOI: 10.1016/0032-5910(91)80021-A |
| [14] | WU Jinsui, YU Boming, YUN Meijuan. A resistance model for flow through porous media[J]. Transport in Porous Media, 2008, 71 (3) : 331-343. DOI: 10.1007/s11242-007-9129-0 |
| [15] | CARMAN P C. Fluid flow through granular beds[M]. 1937 : 150 -166. |
| [16] | SHEFFIELD R E, METZNER A B. Flow of nonlinear fluids through porous media[J]. AICHE J, 1976, 22 (4) : 736-744. DOI: 10.1002/aic.690220416 |
| [17] | MEREDITH R E, TOBIAS C W. Conduction in heterogeneous systems[M]//Advances in Electrochemistry and Electrochemical Engineering 2. New York: Interscience Publishers, 1962. |
| [18] | COMITI J, RENAUD M. A new model for determining mean structure parameters of xed beds from pressure drop measurements: application to beds packed with parallelepipedal particles[J]. Chemical Engineering Science, 1989, 44 (7) : 1539-1545. DOI: 10.1016/0009-2509(89)80031-4 |
| [19] | KOPONEN A, KATAJA M, TIMONEN J. Permeability and effective porosity of porous media[J]. Physical Review E, 1997, 56 (3-BptB) : 3319-3325. DOI: 10.1103/PhysRevE.56.3319 |
| [20] | YU Boming, LI Jianhua. A geometry model for tortuous of flow path in porous media[J]. Chinese Physics Letters, 2004, 21 : 1569-1571. DOI: 10.1088/0256-307X/21/8/044 |
| [21] | TANG Xiaowu, SUN Zufeng, CHENG Guanchu. Simulation of the relationship between porosity and tortuosity in porous media with cubic particles[J]. Chinese Physics B, 2012, 21 (10) : 2011-2018. |
| [22] | PISANI L. Simple expression for the tortuosity of porous media[J]. Transport in Porous Media, 2011, 88 (2) : 193-203. DOI: 10.1007/s11242-011-9734-9 |
| [23] | MEHTA D, HAWLEY M C. Wall effect in packed columns[J]. Industrial & Engineering Chemistry Process Design and Development, 1969 (8) : 280-282. |
| [24] | CHRISTOPHER R H, MIDDLEMAN S. Power-law flow through a packed tube[J]. I & EC Fundamentals, 1965 (4) : 422-426. |
| [25] | KEMBLOWSKI Z, MICHNIEWICS M. A new look at the laminar flow of power law fluids through granular beds[J]. Rheologica Acta, 1979, 18 (6) : 730-739. DOI: 10.1007/BF01533348 |
| [26] | PASCAL H. Non steady flow of non-Newtonian fluids through a porous medium[J]. International Journal of Engineering Science, 1983, 21 : 199-210. DOI: 10.1016/0020-7225(83)90021-6 |
| [27] | SHENOY A V. Darcy-Forchheimer natural, forced and mixed convection heat transfer in non-Newtonian power-law fluid-saturated porous media[J]. Transport in Porous Media, 1993, 11 (3) : 219-241. DOI: 10.1007/BF00614813 |
| [28] | HAYES R E, AFACAN A, BOULANGER B, et al. Modelling the flow of power law fluids in a packed bed using a volume-averaged equation of motion[J]. Transport in Porous Media, 1996, 23 (2) : 175-196. |
 2017, Vol. 49
2017, Vol. 49


