2.航空发动机动力传输航空科技重点实验室(中航工业沈阳发动机设计研究所),沈阳 110015
2.Aviation Key Laboratory of Science andTechnology on Power Transmission of Aeroengine(AVIC Shenyang Engine Design and Research Institute),Shenyang 110015,China
中央传动杆是航空发动机传动系统的重要构件,其功能是在中央传动和附件机匣之间传递功率.中央传动杆两端设计有渐开线花键,仅传递扭矩或承受很小的弯矩,因此结构上被设计成细长轴形式.中央传动杆的动力学特性是影响其性能的重要因素,业内多起碰摩故障和两端花键异常磨损故障均与之有直接关系[1].大涵道比发动机风扇直径较大,中央传动杆长度较长.为提高中央传动杆的临界转速,多采用辅助支点,即中央传动杆三点支承.辅助支点的布置不当同样会导致严重故障,某型发动机的中央传动杆发生过因振动导致的辅助支点轴承破碎故障[1].
目前,单转子的动力学分析理论已日趋成熟[2-6],但鲜有文章从动力学角度对中央传动杆支承进行研究.研究支承形式和相关参数对中央传动杆动力学特性的影响,对于中央传动杆的工程设计有着十分重要的意义[7].
本文建立了中央传动杆的动力学模型,引入陀螺力矩的影响,采用数值分析和试验验证,揭示了中央传动杆的临界转速随辅助支点支承位置和支承刚度的变化规律,为中央传动杆结构设计和支承设计提供了一定的参考和指导.
1 动力学模型及方程的建立 1.1 中央传动杆动力学模型某航空发动机中央传动杆的结构如图 1所示,两端花键插入由滚动轴承支承的齿轮内,中间设有辅助支点,同样由滚动轴承支承.该型中央传动杆竖直装配并穿过发动机的内外涵道,轴向不固定,下端花键处设计有限位轴肩.该型中央传动杆的工作转速为12000〜20000r/min,材料为18Cr2Ni4WA,其物理参数见《中国航空材料手册》[8].
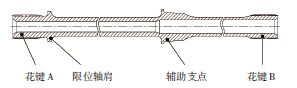
|
图 1 某中央传动杆结构 Figure 1 The structure of a radial driving shaft |
中央传动杆是一个连续的物体,理论上有无穷多个自由度,工程上一般采用近似处理——离散化.本文采用集总参数法对中央传动杆进行离散化,将其简化为由多个无质量、转动惯量的弹性轴段联接的集总质量(节点)所形成的系统[9].
节点越密,计算精度越高,计算量也越大.在满足精度要求的情况下,尽量设置较少的节点.为确定合适的节点密度,对分析对象进行了试算:节点数量由18提高到35后,第一阶固有频率变化了1.56%,节点数量由35提高到52后,第一阶固有频率变化了0.35%.对于该分析对象,工作转速范围内,1%的计算误差可以接受,因此节点数确定为35.
最终建立的动力学模型见图 2,共35个节点,辅助支点位于节点21处.
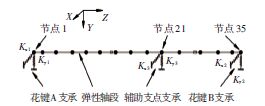
|
图 2 某中央传动杆动力学模型 Figure 2 Dynamic model of a radial driving shaft |
中央传动杆无名义轴向载荷,本文忽略其轴向振动.模型中每个节点有5个自由度:X方向挠度x,绕Y轴的转角φ,Y方向挠度y,绕X轴的转角少ψ,以及绕Z轴的转角θ.
复杂转子的理论分析方法主要有传递矩阵法和有限单元法.在处理转子的支承方面,传递矩阵法较为繁琐[10],有限单元法更为有效[3, 11],因此本文采用有限单元法建立中央传动杆的弯曲动力学方程.轴单元的受力情况见图 3,M、W为弯矩,S、Q为剪切力,$\Sigma M$、$\Sigma N$为节点受到的广义弯矩,$\Sigma {P_x}$、$\Sigma {P_y}$为节点受到的广义外力.根据Euler-Bernoulli梁理论[9],得出X方向轴单元的方程[12]:
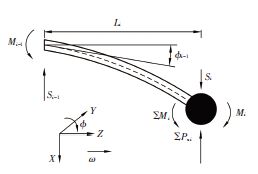
|
图 3 轴段单元的受力分析图 Figure 3 Force analysis of shaft element |
| $\left[ \matrix{ x \hfill \cr \phi \hfill \cr M \hfill \cr S \hfill \cr} \right]_i^R = {\left[ {\matrix{ 1 & L & {{L^2}/L2EI} & { - {L^3}/6EI} \cr 0 & 1 & {L/EI} & { - {L^2}/2EI} \cr 0 & 0 & 1 & { - L} \cr 0 & 0 & 0 & 1 \cr } } \right]_i}\left[ \matrix{ x \hfill \cr \phi \hfill \cr M \hfill \cr S \hfill \cr} \right]_{i - 1}^R + {\left[ \matrix{ 0 \hfill \cr 0 \hfill \cr \Sigma M \hfill \cr \Sigma {P_x} \hfill \cr} \right]_i}.$ | (1) |
式中:上标R表示位置在该轴段的右端面,下标i、i-1表示轴段编号.
陀螺力矩体现在节点的广义弯矩中,广义弯矩方程如下[12]:
| ${\left[ \begin{array}{l} \Sigma M\\ \Sigma N \end{array} \right]_i} = {\left[ {\begin{array}{*{20}{c}} {{J_y}}&0\\ 0&{{J_x}} \end{array}} \right]_i}\left[ \begin{array}{l} {\ddot \phi }\\ {\ddot \psi } \end{array} \right] + {\left[ {\begin{array}{*{20}{c}} 0&{ - {J_z}\omega }\\ {{J_z}\omega }&0 \end{array}} \right]_i}{\left[ \begin{array}{l} {\dot \phi }\\ {\dot \psi } \end{array} \right]_i} + \left[ \begin{array}{l} \Delta M\\ \Delta N \end{array} \right].$ | (2) |
式中:Jx、Jy、Jz分别为节点绕x、y、z轴的转动惯量,ω为传动杆的转动角速度,△M为外力产生的y方向的弯矩,△N为外力产生的x方向的弯矩.
同理可得Y方向的轴单元方程.联立所有节点的弯曲动力学方程,并整合扭转动力学方程,便可获 得弯扭动力学方程$12〜13$:
| $M\ddot{X}+C\dot{X}+KX=F.$ | (3) |
中央传动杆两端由花键约束,径向支承刚度由结构、花键加工误差、载荷共同决定,具有较大的离散性.本文根据工程经验,假定径向支承刚度为K=5×108N/m.根据该型中央传动杆的工作转速,并考虑一定的安全裕度,本文仅关注30000r/min以下的临界转速.
2.1 陀螺力矩的影响分析根据转子动力学理论:转子正进动(Forward,简称F)时,陀螺力矩阻止轴的变形,相当于增加了转子刚度,固有频率有所提高;转子反进动(Backward,简称B)时,陀螺力矩促进轴的变形,相当于降低了转子刚度,固有频率有所下降[14].随着转速的提高,中央传动杆的固有频率出现了分岔现象,如图 4所示.受陀螺力矩的影响,转速提高至20000r/min时,前两阶固有频率分别改变了0.452%和0.456%.因此,在中央传动杆的工作转速范围内,陀螺力矩对固有频率的影响很小.
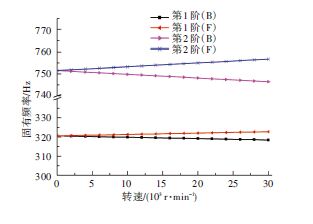
|
图 4 陀螺力矩对前2阶固有频率的影响 Figure 4 The influence of gyroscopic moment on first two orders natural frequency |
针对中间有支点和中间无支点两种情况,通过绘制Campbell图得出了某中央传动杆的临界转速[14-15],结果见表 1,对应的振型见图 5和图 6.
| 表 1 中央传动杆的临界转速 Table 1 Critical speed of radial driving shaft |
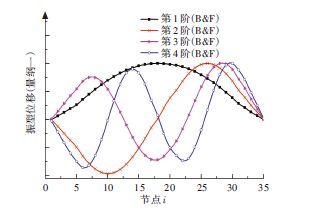
|
图 5 中央传动杆的振型(中间无支点) Figure 5 Vibration mode of radial driving shaft (without intermediate fulcrum) |
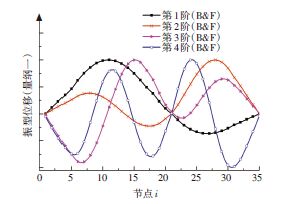
|
图 6 中央传动杆的振型(中间有支点) Figure 6 Vibration mode of radial driving shaft (with intermediate fulcrum) |
中间无支点时,中央传动杆的第1阶临界转速 较低,第2阶临界转速对应振型的“振型节点”位于节点18附近.
中间辅助支点消除了中央传动杆的一弯振型,大幅提升了第1阶临界转速.中央传动杆的第1阶临界转速对应振型的“振型节点”位于节点21,即辅助支点处.
该型中央传动杆的第1阶临界转速在工作转速范围内,且滚动轴承及花键的阻尼很小,因此发动机在起飞或巡航状态时,工作转速接近临界转速,中央传动杆振动水平会很高,该型号多台发动机均曾发生中央传动杆辅助支点轴承破碎的故障[1].中间辅助支点虽可大幅提高中央传动杆的临界转速,但细致的理论分析必不可少.
2.3 中间支点位置的影响分析在其他条件不变的情况下,改变中间支点的位 置,中央传动杆第1阶和第2阶临界转速的变化情况如图 7所示.
该型中央传动杆的轴向不固定,允许一定的窜动量.中央传动杆窜动时,会引起中间支点位置的变化,设计时应尽量降低临界转速对支点位置的灵敏度.由图 7可知:当支点位于节点18(即中间无支点二弯“振型节点”)附近时,中央传动杆第1阶临界转速最大,且对支点位置的灵敏度最小.
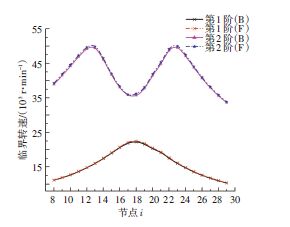
|
图 7 中间支点位置对临界转速的影响 Figure 7 The influence of intermediate fulcrum position on critical speed |
中间支点位于节点21处时,中间支点的支承刚度对中央传动杆临界转速的影响如图 8所示,图中提供了部分临界转速对应的振型.由图 8可知,中间支点的支承刚度对中央传动杆的前两阶临界转速均有影响,当支承刚度大于3×107N/m时,第1阶临界转速趋于稳定.
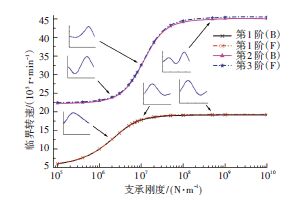
|
图 8 中间支点(节点21)支承刚度对临界转速的影响 Figure 8 The influence of intermediate fulcrum(node 21)supporting stiffness on critical speed |
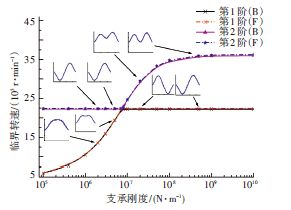
中间支点位于节点18处时(即中间无支点二弯“振型节点”附近时),中间支点的支承刚度对中央传动杆临界转速的影响如图 9所示,图中提供了部分临界转速对应的振型.
由图 9可知,二弯振型对应的临界转速基本无变化,即中间支点的支承刚度对中央传动杆的二弯临界转速基本无影响.当支承刚度大于8×106N/ m时,第1阶临界转速趋于稳定.按本文2.3小节中的分析结论,中间支点位于节点18处时中央传动杆第1阶临界转速最大.综合分析不难发现,通过调整支承位置和支承刚度提高临界转速的手段是有限度的.
中央传动杆的中点辅助支承由滚动轴承实现,中点支承刚度很难实现主动设计.首先,中央传动杆穿过发动机的外涵道,中间支点结构的设计限制较多;其次,滚动轴承的径向运行刚度存在“软化效应",随转速的变化而变化.中间支点设计在节点18处(即中间无支点二弯“振型节点"附近)时,且支承刚度大于8×106N/m时,第1阶临界转速不受支承刚度影响,有利于实现对临界转速的控制.
由图 8和图 9可知,中间支点的支承刚度不宜过小,否则起不到提高临界转速的作用.
|
图 9 中间支点(节点18)支承刚度对临界转速的影响 Figure 9 The influence of intermediate fulcrum(node 18)supporting stiffness on critical speed |
设置中间辅助支点可被认为是振动控制的一种手段.相关研究表明,振幅控制值越小,传递力(即外传力)也就越小[9].当控制点设置在节点18处时(即中间无支点二弯“振型节点"附近时),在第一阶临界转速附近,振幅控制值接近于零,因此中间辅助支点的外传力最小.该特性有利于辅助支点轴承的设计.
3 试验验证与讨论为验证中央传动杆动力学模型和方程的准确性,开展了某中央传动杆临界转速的验证试验.受试验设备最高转速的限制,取消了中间辅助支点.
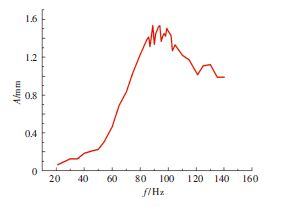
中央传动杆试验器最高转速8700r/min,采用两个电涡流位移传感器监控中央传动杆的径向振动幅值A,传感器垂直布置且与试验件表面的距离为1.5mm.
试验结果如图 10所示,横坐标为中央传动杆转动频率,纵坐标为轴心位移.试验后发现位移传感器被试验件碰偏,结合图 10判断碰撞发生时传动杆的转动频率约为86Hz,推测中央传动杆的临界转速在86~100Hz,即5160~6000r/min.
|
图 10 轴心涡动幅值 Figure 10 Amplitude of shaft center whirl |
理论计算的第1阶临界转速为5356或5397r/min,与试验结果一致性较好,支持了中央传动杆动力学计算方法的正确性.
4 结论(1) 本文建立的中央传动杆动力学理论分析方法及获得的计算结果能够较真实地反映中央传动杆实际情况,验证试验支持了这一结论.
(2) 在某中央传动杆的工作转速内,陀螺力矩对其固有频率的影响很小,不大于0.5%.
(3) 设置中间辅助支点是提高中央传动杆临界转速的一种有效手段,但支承刚度应大于特定值.
(4) 中间辅助支点的位置对临界转速的影响很大.将中间辅助支点设置在中间无支点时的二弯“振型节点"处,可获得最高的临界转速,最低的支承位置灵敏度,以及最大的支承刚度设计裕度.
| [1] |
陈聪慧.
航空发动机机械系统常见故障[M]. 北京: 航空工业出版社, 2013 : 29 -64.
CHEN Conghui. The common failures of aero-engine mechanical system[M]. Beijing: Aviation Industry Press, 2013 : 29 -64. |
| [2] |
孟光. 转子动力学研究的回顾与展望[J].
振动工程学报, 2002, 15 (1) : 1-9.
MENG Guang. Retrospect and prospect to the research on rotordynamics[J]. Journal of Vibration Industry Press, 2002, 15 (1) : 1-9. |
| [3] | NELSON H D, MC-VAUGH J M. The dynamics of rotor bearing systems using finite elements[J]. Journal of Engineering, 1976, 98 (2) : 593-600. DOI: 10.1115/1.3438942 |
| [4] | ZORZI E S, NELSON H D. Finite element simulation of rotor bearing systems with internal damping[J]. Journal of Engineering for Power, 1977, 99 (1) : 71-76. DOI: 10.1115/1.3446254 |
| [5] | LAI M, TIWARI R. Identification of multiple faults with Incomplete response measurements in rotor-bearing-coupling Systems[C]// Proceedings of the ASME Turbine Expo. Mumbai: ASME, 2012. |
| [6] | MA W M, WANG J J, Dynamic analysis of anisotropic asymmetric rotor-bearing system based on three-dimensional finite element method[C]// Proceedings of ASME Turbo Expo 2014. Düsseldorf: ASME, 2014: 150f16.DOI:10.1115/GT2014-25304. http://proceedings.asmedigitalcollection.asme.org/volume.aspx?volumeid=16690 |
| [7] | QUEITZSCH G K Jr, FLEMING D P. Rotordynamic influence on rolling element bearing selection and operation$R$. Washington: NASA, 2001:2001-211131. http://cn.bing.com/academic/profile?id=9a4699ea256fca98a883a7185b94f48a&encoded=0&v=paper_preview&mkt=zh-cn |
| [8] |
《中国航空材料手册》编辑委员会.
中国航空材料手册: 第1卷[M]. 北京: 中国标准出版社, 2002 : 76 -87.
China Aeronautical Materials Handbook Editorial Board. China aeronautical materials handbook: volume 1[M]. Beijing: China Standard Press, 2002 : 76 -87. |
| [9] |
虞烈, 刘恒.
轴承-转子系统动力学[M]. 西安: 西安交通大学出版社, 2001 : 129 -165.
YU Lie, LIU Heng. Bearing-rotor system dynamics[M]. Xi’an: Xi’an Jiaotong University, 2001 : 129 -165. |
| [10] | VARNEY P, GREEN I. Rotordynamic analysis using the complex transfer matrix[C]//Proceeding of the ASME Design Engineering Technical conference. Chicago: ASME, 2012: 237-246. DOI:10.1115/DETC2012-70643. http://cn.bing.com/academic/profile?id=a4a9a3e420871d3a11affff07e312291&encoded=0&v=paper_preview&mkt=zh-cn |
| [11] | NELSON H D. A finite rotating shaft element using Timoshenko Beam theory[J]. Journal of Mechanical Design, 1980, 102 (4) : 793-803. DOI: 10.1115/1.3254824 |
| [12] |
欧卫林, 王三民, 袁茹. 齿轮耦合复杂转子系统弯扭耦合振动分析的轴单元法[J].
航空动力学报, 2005, 20 (3) : 434-439.
OU Weilin, WANG Sanmin, YUAN Ru. Shaft element method for the analysis of lateral-torsional conpling vibration of a complex gear-rotor system[J]. Journal of Aerospace Power, 2005, 20 (3) : 434-439. |
| [13] |
李楠, 王三民, 杜佳佳. 功率四分支齿轮传动系统的固有特性与动载系数[J].
航空动力学报, 2013, 28 (2) : 445-451.
LI Nan, WANG Sanmin, DU Jiajia. Natural characteristics and dynamic load coefficient of power four embranchments gear transmission[J]. Journal of Aerospace Power, 2013, 28 (2) : 445-451. |
| [14] | HSU C N, CHIANG H W. Rotor dynamics analysis and testing of a turbomolecular pump rotor-bearing system[C]//Proceedings of ASME Turbo Expo 2011. Vancouver: ASME, 2011: 409-416. DOI: 10.1115/GT2011-46. |
| [15] | DIMOND T, CHAUDHRY J, WAGNER M, et al. Rotordynamic analysis of a rotor-disk system including a synchronously reduced modal[C]//Proceedings of the ASME Design Engineering Technical Conference. Portland: ASME, 2013: DOI: 10.1115/DETC2013-13699. |
 2017, Vol. 49
2017, Vol. 49


