航空发动机轴承腔中,润滑油被滚动轴承离散成油滴,油滴在腔内空气中高速运动并最终碰撞到腔壁上,沉积后形成油膜.由于油滴、空气和腔壁的温度差异比较大,油气介质之间以及它们与腔壁之间还存在着热量交换.准确地预测轴承腔中复杂的油气两相流动和换热状态是进行轴承腔润滑和换热设计的重要工作.
轴承腔中油滴碰撞腔壁沉积特性是分析腔壁油膜流动和换热状态的基础条件,很多学者开展了这方面的分析工作. Glahn等[1]初次使用相位多普勒粒子分析(Phase Doppler Particle Analyzer,PDPA)技术测量了轴承腔中油滴的尺寸和初始速度,使用拉格朗日参考系向前积分动量方程计算了油滴的轨迹和速度. Simmons等[2-3]采用拉格朗日追踪方法计算了油滴运动,其研究表明,尺寸较小的油滴在空气中运动时受空气的影响较大. 以上工作确定了轴承腔中油滴运动至腔壁时的速度等参数,为开展油滴碰撞腔壁沉积特性分析提供了条件. Farrall等[4]则确定了轴承腔中油滴碰撞腔壁的飞溅与沉积过渡准则,给出了油滴碰撞腔壁后不同变化状态的定量描述,并探讨了油滴初始条件对油滴碰撞腔壁沉积作用的影响[5]. 王军等[6]分析了轴承腔运动油滴的受力情况,根据牛顿第二定律建立了油滴运动方程,并采用差分方法计算了油滴在腔内运动以及碰撞腔壁的速度,分析了单一尺寸油滴在腔壁的沉积特性. Chen等[7]将轴承腔油滴沉积特性以及轴承腔壁面油膜流动等进行了串行分析,提出了轴承腔油滴和壁面油膜物理特性研究的一种新途径. 吕亚国等[8]建立了腔内油滴和空气的双向耦合计算模型,实现了腔内油气两相流动特性的分析. 孙恒超等[9-10]在考虑油滴与空气对流换热的条件下开展了轴承腔油滴运动速度和温度的分析,但并未关注油滴碰撞腔壁沉积特性. 刘登等[11]建立了轴承腔中运动油滴与壁面斜碰撞及油膜铺展的数值计算模型,分析了油滴与壁面碰撞后的油膜铺展特征. 迄今有关轴承腔中油滴运动及碰撞腔壁沉积特性分析的工作中,很少涉及油滴在空气中运动的温度计算,也未开展油滴碰撞腔壁热量交换以及沉积热量的分析. 这使油滴沉积质量和动量分析的准确性有所降低;因缺少油滴碰撞腔壁沉积热量的输入条件,也限制了轴承腔壁面油膜流动温度分析工作的实施.
本文在油滴运动及温度计算的基础上开展了轴承腔油滴碰撞腔壁沉积特性分析. 梳理了油滴碰撞腔壁沉积准则,给出了区分油滴碰撞腔壁“粘附"、“反弹"、“扩散"以及“破裂"等不同沉积现象的定量描述,并确定了不同沉积现象时油滴的沉积质量和动量特性. 以油滴碰撞腔壁时对腔壁的冷却效率为基础,借助热量守恒条件,确定了不同沉积现象时油滴的沉积热量特性. 最后讨论了工况条件对油滴碰撞腔壁沉积质量、动量以及热量特性的影响.
1 油滴碰撞腔壁沉积特性分析文献[9-10]开展了轴承腔中油滴运动过程中速度和温度的分析,在考虑油滴与腔内空气热量交换的条件下确定了油滴运动至腔壁时的油滴直径、速度、温度以及润滑油物性参数等.本文即在文献[9-10]的基础上开展了油滴碰撞腔壁沉积特性分析.
1.1 油滴碰撞腔壁沉积准则轴承腔中油滴在运动至腔壁位置处,会以一定的速度碰撞轴承腔壁面,并因油滴的直径、速度以及润滑油的物性参数等的不同而产生不同的碰撞状态. Mundo等[12]研究了液滴碰撞固体壁面产生的沉积现象,根据他的研究结果可推断轴承腔中油滴与腔壁碰撞的状态.
Mundo等[13]通过观测液滴与固体壁面碰撞沉积现象,建立了液滴碰撞固体壁面的沉积准则.根据其研究结论可以确定轴承腔中油滴与腔壁碰撞的沉积准则,并通过量纲一的飞溅参数B表示:
| $B = W{e_d}^{0.5}{{\mathop{\rm Re}\nolimits} _d}^{0.25}$ |
式中,Wed和Red分别是油滴入射腔壁时的韦伯数和雷诺数,且
| $\eqalign{ & W{e_d} = {\rho _d}{u_{dr}}^2d/\sigma ,\cr & {{\mathop{\rm Re}\nolimits} _d} = {\rho _d}{u_{dr}}^2d/{\mu _d}. \cr} $ |
其中,ρd、μd和σ分别是油滴入射腔壁时的密度、动力黏度和表面张力,将油滴入射腔壁时的温度Td代入润滑油随温度的变化关系式即可确定这些物性参数;dd和udr分别是油滴入射腔壁时的直径和径向速度. 这里确定油滴与腔壁碰撞沉积准则时,考虑了油滴自轴承向腔壁运动过程中温度变化的实际情况,包含了温度变化对滑油物性、油滴直径以及油滴轨迹和速度的影响,这种包含温度效应的油滴沉积特性分析方法提升了确定油滴入射腔壁状态参数的计算精度,也在一定程度上可以提升油滴沉积特性分析的准确性.
如图 1所示,当B≤57.7时,油滴与腔壁碰撞后不破裂,且细分为3种不同的状态:当Wed≤5时,油滴粘附在腔壁上;当5d≤10时,油滴从腔壁上反弹离开腔壁;而当Wed>10时,油滴以扩散油膜的形式附着在腔壁上.当B>57.7时,油滴与腔壁碰撞后产生破裂,破裂后的油滴一部分以油膜形式铺展在腔壁上,另一部分进一步破裂形成二次油滴.

|
图 1 轴承腔油滴与腔壁碰撞沉积准则 Figure 1 Transition criteria for droplet/housing interaction in abearing chamber |
油滴与腔壁碰撞后不破裂,油滴的全部质量转移至腔壁形成油膜,油滴的径向动量在碰撞时被消耗,切向动量转移至腔壁油膜,油滴的热量及碰撞腔壁时从腔壁吸收的热量转移至腔壁油膜.
油滴与腔壁碰撞产生破裂,破裂油滴直接沉积部分质量至腔壁形成油膜,其径向动量被消耗,但切向动量转移至腔壁油膜.同样地,沉积部分的热量及碰撞腔壁时从腔壁吸收的热量转移至腔壁油膜.碰撞腔壁飞溅形成的二次油滴中,部分再次沉积为油膜,另一部分从通风口排出轴承腔.二次油滴的速度是杂乱无章的,故可认为二次油滴的动量相互抵消,二次油滴再次沉积时没有动量转移至腔壁油膜.二次油滴再次沉积时,沉积部分的热量及碰撞腔壁时从腔壁吸收的热量也会转移至腔壁油膜.
结合图 1可以确定油滴与腔壁碰撞沉积质量、动量和热量情况.沉积质量:当油滴不破裂时,最终沉积至腔壁的质量即碰撞腔壁前油滴的质量md;当油滴破裂时,最终沉积至腔壁的质量即首次碰撞腔壁沉积的质量(md-msd)与二次油滴再次沉积质量msdc之和. 沉积动量:当油滴不破裂时,最终沉积至腔壁的动量即mdudt;当油滴破裂时,最终沉积至腔壁的动量即(md-msd)udt. 沉积热量:当油滴不破裂时,最终沉积至腔壁的热量即mdcvlTd';当油滴破裂时,最终沉积至腔壁的热量即(md-msd)cvlTd'与msdccvlTd″之和.
为了更好地评估油滴与腔壁碰撞沉积质量、动量和热量的变化情况,在此引入油滴碰撞腔壁的质量沉积率、动量沉积率和热量沉积率的概念.
1.2 质量和动量沉积率油滴与腔壁碰撞后,不包含飞溅的二次油滴再次沉积的质量,沉积部分的质量与碰撞前油滴质量的比值为油滴一次质量沉积率η1. 计入二次油滴再次沉积的质量后,沉积的总质量与碰撞前油滴质量的比值为油滴质量沉积率η.Chen等[7]根据Farrall等[5]的分析确定了油滴质量沉积率η1和η的表达式
| $\eqalign{ & {\eta _1} = \left\{ \matrix{ 1,B \le 57.7; \hfill \cr 1 - 8.03 \times {10^{ - 11}}{B^{4.1718}},57.7 < B <\le 200; \hfill \cr 0.1 + {5.792_e}^{ - 1.15 \times {{10}^{ - 2}}B},B > 200. \hfill \cr} \right. \cr & \eta = \left\{ \matrix{ 1,B \le 57.7; \hfill \cr 1 - (1 - {\varepsilon _L})8.03 \times {10^{ - 11}}{B^{4.1718}},57.7 < B \le 200; \hfill \cr 1 - (1 - {\varepsilon _L})(0.9 - {5.792_e}^{ - 1.15 \times {{10}^{ - 2}}B}),B > 200. \hfill \cr} \right. \cr} $ |
式中εL是二次油滴再次沉积质量与二次油滴总质量的比值[7].
油滴动量沉积率是油滴与腔壁碰撞后,沉积部分转移到油膜的动量与油滴自轴承甩出时初始动量的比值.分析中不考虑二次油滴的动量转移,油滴动量沉积率为
| $\xi = {{{\eta _1}{m_d}{u_{dtz}}} \over {{m_d}{u_{{d_0}}}}} = {\eta _1}{{{u_{dtz}}} \over {{u_{{d_0}}}}}.$ |
式中:udtz是油滴碰撞腔壁时的切向速度,ud0是油滴自轴承甩出时的速度.
1.3 热量沉积率Pasandideh等[14]分析了液滴碰撞热壁面时对壁面的冷却现象,并给出了液滴碰撞热壁面时对壁面冷却效率与液滴参数的关系.根据Pasandideh的研究方法可以分析轴承腔中油滴碰撞轴承腔腔壁时的热量沉积率.定义油滴碰撞腔壁时对腔壁的冷却效率为
| ${\varepsilon _c} = {{{q_c}} \over {{m_d}{c_{vl}}({T_W} - {T_d})}}.$ |
式中:qc是油滴碰撞腔壁时与腔壁的热交换量,Tw是腔壁的温度,Td是碰撞腔壁前油滴的温度,cvl是温度为Tw和Td均值时润滑油的比热容.
油滴碰撞腔壁时对腔壁的冷却效率εc与油滴碰撞腔壁时的工况参数之间的关系为
| ${{\varepsilon }_{c}}=\frac{2}{{{\underset{d}{\mathop{\Pr }}\,}^{0.6}}}\left[ \frac{W{{e}_{d}}+12}{3(1-cos{{\theta }_{a}})R{{e}_{d}}^{0.5}+4W{{e}_{d}}} \right].$ |
式中:Prd是油滴的普朗特数,θa是润滑油与腔壁的接触角.
根据油滴碰撞腔壁时对腔壁的冷却效率可以推导油滴碰撞腔壁时的热量沉积率.
油滴从轴承甩出时的热量e0=mdcvl(Td0)Td0,cvl(Td0)表示温度Td0时润滑油的比热容,Td0是油滴从轴承甩出时的温度.碰撞腔壁前油滴的热量e=mdcvl(Td)Td.这里考虑了油滴自轴承运动至腔壁时比热容随油滴温度的变化.当油滴碰撞腔壁不破裂时,碰撞腔壁后油滴沉积的热量e'=mdcvl(Td')Td'.由于cvl(Td')和Td'是相互依赖的,cvl随温度的变化不大,所以这里忽略油滴碰撞腔壁时因温度变化而引起的滑油比热容的变化,即认为Td'≈Td.因此热量沉积率γ为
| $\gamma = {{e'} \over {{e_0}}} = {{{c_{v1}}({T_d}){T_d}} \over {{c_{v1}}({T_{{d_0}}}){T_{{d_0}}}}}{{{T_d}'} \over {{T_d}}}.$ |
可见,热量沉积率γ的一部分是由于油滴在空气中运动由空气给予的热量引起的,将这一部分称为其运动热量变化率${{\gamma }_{0}}={{c}_{v1}}({{T}_{d}}){{T}_{d}}/\left[ {{c}_{v1}}({{T}_{{{d}_{0}}}}){{T}_{{{d}_{0}}}} \right].$另一部分Td'/Td则体现了油滴碰撞腔壁时热量的变化.
忽略油滴碰撞腔壁时润滑油与空气间的热交换量以及黏性耗散热后,根据热量守恒条件,即油滴碰撞腔壁时热量的变化等于润滑油与腔壁的热交换量,有如下表达式:
| ${m_d}{c_{v1}}{T_d}' - {m_d}{c_{v1}}{T_d} = {\varepsilon _c}({m_d}{c_{v1}}{T_w} - {m_d}{c_{v1}}{T_d}),$ | (1) |
改写式(1)为
| ${{{T_d}'} \over {{T_d}}} = 1 + {\varepsilon _c}({{{T_w}} \over {{T_d}}} - 1).$ |
因此,油滴碰撞腔壁时的热量沉积率
| $\gamma =\frac{{{c}_{v1}}({{T}_{d}}){{T}_{d}}}{{{c}_{v1}}({{T}_{{{d}_{0}}}}){{T}_{{{d}_{0}}}}}\left[ 1+{{\varepsilon }_{c}}(\frac{{{T}_{w}}}{{{T}_{d}}}-1)\text{ } \right].$ | (2) |
当油滴碰撞腔壁破裂时,碰撞腔壁后油滴首次沉积部分的热量$e' = {\eta _1}{m_d}{c_{v1}}{T_d}'$,二次油滴的总热量${e_{sd = }}{m_{sd}}{c_{v1}}{T_{sd}}$,二次油滴再次沉积部分的热量${e_{sdc}} = {m_{sdc}}{c_{v1}}{T_d}''$.这里的cvl也是温度为Td时润滑油的比热容,并且${m_{sde}}/{m_d} = \eta - {\eta _1}$.则热量沉积率γ为
| $\gamma = {{e' + {e_{sdc}}} \over {{e_0}}} = {{{\eta _1}{T_d}' + (\eta - {\eta _1}){T_d}''} \over {{T_d}}}{{{c_{v1}}({T_d}){T_d}} \over {{c_{v1}}({T_{{d_0}}}){T_{{d_0}}}}}.$ |
这种情况下的油滴的运动热量变化率γ0与油滴不破裂时的计算方式相同. 同样根据热量守恒条件,可以确定
| ${\eta _1}{m_d}{c_{v1}}{T_d}' + (\eta - {\eta _1}){m_d}{c_{v1}}{T_d}'' + (1 - \eta ){m_d}{c_{v1}}{T_{sd}} - {m_d}{c_{v1}}{T_d} = {\varepsilon _c}({m_d}{c_{v1}}{T_w} - {m_d}{c_{v1}}{T_d}).$ | (3) |
改写式(3)为
| ${{{\eta _1}{T_d}' + (\eta - {\eta _1}){T_d}''} \over {{T_d}}} = 1 + {\varepsilon _{\rm{c}}}({{{T_w}} \over {{T_d}}} - 1) - (1 - \eta ){{{T_{sd}}} \over {{T_d}}},$ |
因此,油滴碰撞腔壁时的热量沉积率γ为
| $\gamma =\frac{{{c}_{v1}}({{T}_{d}}){{T}_{d}}}{{{c}_{v1}}({{T}_{{{d}_{0}}}}){{T}_{{{d}_{0}}}}}\left[ 1+{{\varepsilon }_{\text{c}}}(\frac{{{T}_{w}}}{{{T}_{d}}}-1)-(1-\eta )\frac{{{T}_{sd}}}{{{T}_{d}}} \right].$ | (4) |
目前,还缺少关于油滴碰撞腔壁后形成的二次油滴的温度Tsd的理论和试验研究,其他研究领域中也未见关于液滴撞壁形成的二次液滴温度研究的报道.可以推断二次油滴的温度Tsd介于撞壁前油滴温度Td和壁面温度Tw之间,因此本文中假定${T_{sd}} = ({T_d} + {T_w})/2$.
2 结果与讨论本文进行油滴碰撞腔壁沉积特性分析时,除讨论工况参数的影响外,各参数值如下:转子转速ns=10000r/min,轴承腔高度hb=28mm,转子半径rs=62mm,轴承腔宽度wb=20mm,进气温度T1i=378.15K,润滑油温度Tli=333.15K,使用的润滑油为4109号航空润滑油,其物性参数随温度的变化关系可以参阅文献[15],腔壁温度Tw=483.15K,转子壁面温度Ts=368.15K,油滴从轴承甩出时的初始直径dd0=100μm.如表 1所示,根据文献[9-10]的研究方法,可以确定不同工况条件下油滴碰撞腔壁前的相关参数.
| 表 1 不同工况条件下碰撞腔壁前油滴参数 Table 1 The droplet parameters before impact with housing under different conditions |
在确定碰撞腔壁前油滴参数的基础上,可以开展油滴碰撞腔壁沉积特性分析,这里主要讨论转子转速、油滴直径和进气温度对油滴沉积特性的影响.
图 2是转子转速对油滴沉积特性的影响.

|
图 2 转子转速对油滴沉积特性的影响 Figure 2 Effect of rotor speed on droplet deposition character |
从图 2(a)中可以看出,油滴的一次质量沉积率虽然<1,但是较为接近于1.这说明在所涉及的工况条件下,油滴碰撞腔壁时虽然产生了破裂,但破裂形成的二次油滴的总质量很少.而质量沉积率几乎等于1,这说明油滴碰撞腔壁时,几乎所有质量都沉积至腔壁上.油滴沉积至腔壁的动量约为油滴从轴承甩出时初始动量的一半.从考虑温度效应和不考虑温度效应的对比可以看出,考虑温度效应后,油滴的质量沉积率和动量沉积率均略有降低.这是因为考虑温度效应后,油滴被空气加热,使其直径有所增大,大直径的油滴碰撞腔壁破裂程度加剧,致使油滴沉积质量减少,加之考虑温度效应后油滴运动速度更低,所以油滴沉积动量会更少.
从图 2(b)中可以看出,因油滴在运动过程中被空气加热,油滴在碰撞腔壁之前其热量约增加了15%.由于碰撞腔壁时与腔壁存在强烈的换热作用,油滴的热量明显增加,在碰撞腔壁后,油滴沉积的热量约为其从轴承甩出时初始热量的3倍.
从图中油滴沉积特性随转子转速的变化可以看出,随着转子转速的增加,油滴的质量、动量和热量沉积率均有所降低.转子转速增加后,油滴速度增加、动量增大,与腔壁碰撞更为剧烈,油滴破裂程度增加,所以一次质量沉积率降低. 一次质量沉积率的降低也会使动量沉积率降低.转子转速增加后,油滴在空气中停留时间变短,从空气中吸收的热量减少,所以油滴的运动热量变化率降低,碰撞腔壁时吸收的热量变化不大,热量沉积率会因运动热量变化率的降低而减少.
图 3是油滴直径对油滴沉积特性的影响.从图 3(a)中可以看出,直径<100μm的油滴碰撞腔壁时一次质量沉积率为1,所以油滴是不破裂的.而直径较大油滴的一次质量沉积率<1,所以油滴会破裂形成二次油滴,并且随着油滴直径的增加,破裂形成二次油滴的质量会明显增加.直径为400μm的油滴碰撞腔壁时,会有接近80%的质量飞溅形成二次油滴.但几乎全部二次油滴最终会再次沉积至腔壁,即不同直径油滴碰撞腔壁时的质量沉积率均接近于1.

|
图 3 油滴直径对油滴沉积特性的影响 Figure 3 Effect of droplet diameter on droplet deposition character |
而动量沉积率随着的油滴直径的增加呈现出先增加后降低的变化趋势,其分界点对应的油滴直径大约为100 μm. 这是因为当油滴直径<100 μm时,油滴碰撞腔壁的速度会随着油滴直径的增加而显著增加,所以动量沉积率增加. 而当油滴直径<100 μm时,油滴速度随油滴直径的变化变得微弱,但是一次质量沉积率对动量沉积率的影响占主导地位,动量沉积率会随着一次质量沉积率的降低而明显降低. 从图 3(a)中还可以看出,考虑温度效应与否油滴的质量以及动量沉积率的差异在较小的范围内,这也说明第1节认为二次油滴的温度Tsd介于撞壁前油滴温度Td和壁面温度Tw之间的推断是比较合理的.
从图 3(b)中可以看出,由于小直径油滴在气相介质中运动时间很长,所以油滴运动热量变化非常明显. 或许是因为小直径的油滴碰撞腔壁时铺展油膜更薄而极易被热腔壁加热的缘故,小直径油滴沉积至腔壁后的热量是其初始热量的近20倍. 当油滴直径约>100 μm时,因油滴的速度以及碰撞腔壁的铺展情况差异不大,导致油滴运动的热量变化率和热量沉积率均变化不大.
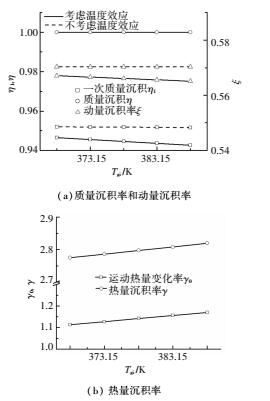
图 4是进气温度对油滴沉积特性的影响.从图 4(a)可以看出,随着进气温度的增加,考虑温度效应后,油滴的一次质量沉积率和动量沉积率略有降低.这是因为考虑温度效应后,油滴在气相介质运动时受空气加热而体积膨胀,使其在碰撞腔壁时,破裂产生更多的二次油滴,所以一次质量沉积率降低,一次质量沉积率的降低使一次沉积质量减少,故动量沉积率也就随之降低.一次质量沉积率和动量沉积率随进气温度的这种变化趋势,在不考虑温度效应时是没有体现的,这也说明考虑温度效应在一定程度上能提升对油滴沉积特性预测的准确性.图 4(b)反映出的规律较为容易理解,随着进气温度的增加,油滴在气相介质运动时吸收了更多的热量,因此其运动热量变化率和热量沉积率均有所增加.
|
图 4 进气温度对油滴沉积特性的影响 Figure 4 Effect of air inlet temperature on droplet deposition character |
此外,综合分析图 2(b)、图 3(b)和图 4(b)中热量沉积率可以看出,不同工况条件下轴承腔中油滴的热量沉积率与运动热量变化率的比值均约为2.5.结合式(2)和(4)的表达式以及质量沉积率η≈1,可以认为出现这一现象的原因或为量纲一的参数εc(Tw/Td-1)的数值受轴承腔工况参数的影响很小.
3 结论1) 考虑油滴在腔内运动温度效应后,油滴碰撞腔壁的质量沉积率和动量沉积率均略有降低;并且考虑温度效应后,可以体现进气温度对质量沉积率和动量沉积率的影响.
2) 转子转速增加后,油滴碰撞腔壁的质量、动量和热量沉积率均有所降低;油滴直径增加后,油滴的一次质量、动量和热量沉积率有所降低,但总质量沉积率变化不大;随着进气温度的增加,油滴的热量沉积率增加,而质量和动量沉积率变化不明显.
目前,还缺少关于轴承腔中油滴碰撞腔壁沉积特性的试验研究,探索并开展油滴沉积特性的试验分析技术,亦是提升对油滴碰撞腔壁沉积复杂物理现象认识以及完善相关研究体系的另一途径.
| [1] | GLAHN A, KURRECK M, WILLMANN M, et al. Feasibility study on oil droplet flow investigations inside aero engine bearing chambers: PDPA techniques in combination with numerical approaches[J]. Journal of Engineering for Gas Turbines and Power, 1996, 118 (4) : 749-755. DOI: 10.1115/1.2816990 |
| [2] | SIMMONS K, HIBBERD S, WANG Yi, et al. Numerical study of the two-phase air/oil flow within an aero-engine bearing chamber model using a coupled Lagrangian droplet tracking method[C]//Proceeding of ASME Pressure Vessels and Piping Conference. New York: American Society of Mechanical Engineers, 2002: 325-331. |
| [3] | FARRALL M, SIMMONS K, HIBBERD S, et al. Computational investigation of the airflow through a shrouded bevel gear[C]//Proceedings of ASME Turbo Expo. New York: American Society of Mechanical Engineers, 2005: 1259-1265. |
| [4] | FARRALL M, HIBBERD S, SIMMONS K. Modelling oil droplet/film interaction in an aero-engine bearing chamber[C]//9th International Conference on Liquid Atomization and Spray Systems. Sorrento: ILASS international, 2003: 13-17. |
| [5] | FARRALL M, HIBBERD S, SIMMONS K. The effect of initial injection conditions on the oil droplet motion in a simplified bearing chamber[J]. Journal of Engineering for Gas Turbines and Power, 2008, 130 (1) : 12501-12507. DOI: 10.1115/1.2770480 |
| [6] |
王军, 陈国定, 刘亚军. 航空发动机轴承腔中油滴运动与沉积的特性分析[J].
摩擦学学报, 2010, 30 (4) : 361-366.
WANG Jun, CHEN Guoding, LIU Yajun. Analysis of the oil droplet motion and deposition characteristics in an aeroengine bearing chamber[J]. Tribology, 2010, 30 (4) : 361-366. DOI: 10.16078/j.tribology.2010.04.016 |
| [7] | CHEN Guoding, SUN Hengchao, WANG Jun. Research into configuration and flow of wall oil film in bearing chamber based on droplet size distribution[J]. Chinese Journal of Aeronautics, 2011, 24 (3) : 355-362. DOI: 10.1016/S1000-9361(11)60042-3 |
| [8] |
吕亚国, 张美华, 刘振侠, 等. 航空发动机轴承腔油气两相流流动数值研究及验证[J].
航空动力学报, 2014, 29 (11) : 2751-2757.
LV Yaguo, ZHANG Meihua, LIU Zhenxia, et al. Numerical study and validation for two-phase flow of oil and gas in aero-engine bearing cavity[J]. Journal of Aerospace Power, 2014, 29 (11) : 2751-2757. DOI: 10.13224/j.cnki.jasp.2014.11.029 |
| [9] |
孙恒超, 陈国定, 王莉娜, 等. 轴承腔油滴含率及油滴相与空气能量传递分析[J].
航空学报, 2016, 37 (3) : 1060-1073.
SUN Hengchao, CHEN Guoding, WANG Li’na, et al. Oil droplets fractions and oil droplets/air energy transfer analysis in bearing chamber[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37 (3) : 1060-1073. DOI: 10.7527/S1000-6893.2015.0086 |
| [10] | SUN Hengchao, CHEN Guoding, ZHANG Yonghong, et al. Theoretical and experimental study on the motion and thermal states of oil droplet in a bearing chamber[J]. Journal of Aerospace Engineering, 2016, 230 (14) : 2596-2614. DOI: 10.1177/0954410016629690 |
| [11] |
刘登, 陈国定, 孙恒超. 运动油滴/固体壁面斜碰撞及油膜铺展的数值模拟[J].
机械科学与技术, 2015, 34 (7) : 1135-1139.
LIU Deng, CHEN Guoding, SUN Hengchao. Numerical simulation of oil droplet impacting and spreading on inclined solid wall[J]. Mechanical Science and Technology for Aerospace Engineering, 2015, 34 (7) : 1135-1139. DOI: 10.13433/j.cnki.1003-8728.2015.0734 |
| [12] | MUNDO C, SOMMERFELD M, TROPEA C. Droplet-wall collisions: experimental studies of the deformation and breakup process[J]. International Journal of Multiphase Flow, 1995, 21 (2) : 151-173. DOI: 10.1016/0301-9322(94)00069-V |
| [13] | MUNDO C, TROPEA C, SOMMERFELD M. Numerical and experimental investigation of spray characteristics in the vicinity of a rigid wall[J]. Experimental Thermal and Fluid Science, 1997, 15 (3) : 228-237. DOI: 10.1016/S0894-1777(97)00015-0 |
| [14] | PASANDIDEH F M, AZIZ S D, CHANDRA S, et al. Cooling effectiveness of a water drop impinging on a hot surface[J]. International Journal of Heat and Fluid Flow, 2001, 22 (2) : 201-210. DOI: 10.1016/S0142-727X(00)00086-2 |
| [15] |
林基恕. 传动及润滑系统[M]//航空发动机设计手册:第12册.北京:航空工业出版社,2002:456-457.
LIN Jishu. System of transmission and lubrication[M]//Manual of aero engine design: volume 12. Beijing: Press of Aviation Industry, 2002:456-457. |
 2017, Vol. 49
2017, Vol. 49


