通常,转速在3 000 r/min、线速度在22m/s(AGMA规定3 600 r/min、25.4 m/s)以上的齿轮传动件被称为高速齿轮[1]. 高速齿轮的轮齿交替啮合频率高,齿面滑动速度大,对齿轮的抗承载能力、抗胶合能力、低振动低噪音等诸多方面要求苛刻. 然而,长期以来,高速齿轮修形设计多数基于经验公式,难以得到精确的设计参数[2-3].
近些年,国内外在齿轮啮合仿真、齿面优化修形等方面的研究发展迅速,众多研究成果给设计人员选取精确设计参数提供了充裕数据. Litvin等[4-6]完善了齿面接触分析(TCA)技术,通过刀具抛物线修形进行齿面修形仿真;方宗德等[7-9]应用Litvin的齿轮啮合理论,推导了斜齿轮在修形和误差条件下的齿面接触分析、边缘接触分析,以及承载接触分析(LTCA);王成[10]、蒋进科[11]等以TCA和LTCA为基础,完成了外啮合斜齿和人字齿的优化修形仿真;唐进元等[12]构建了含安装误差的主动轮鼓形齿的TCA仿真模型. 但是,这些研究主要集中在外啮合方面,且多以单一目标进行齿面优化.
相比外啮合,内啮合结构更加紧凑,且传动效率更高,故日益受到重视. 目前,高速内啮合人字齿轮传动在国外航空核心部件中已经成熟应用,如:GTF发动机中的风扇齿轮驱动系统,其主动轮和内齿圈转速分别高达约8 000~10 000 r/min和3 000~4 000 r/min[13-16]. 然而,相关内啮合传动的高端应用在国内尚属预研阶段,因此对高速内啮合齿面仿真计算的研究,其重要意义不言而喻.
本文基于高速内啮合人字齿仿真计算,对主动轮齿面进行三维修形(齿廓、齿向),通过遗传算法得到精确修形量,实现降低承载传动误差幅值(ALTE)、均匀齿面载荷、降低齿面闪温的多目标优化.
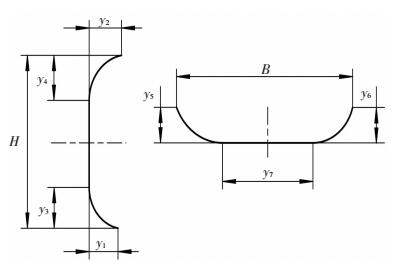
1 修形齿面的构造 1.1 三维修形曲面设计三维修形为齿廓、齿向修形的叠加,修形曲线示意图如图 1所示:齿廓4个参数,齿向3个参数.修形曲线由两段二次抛物线和一段直线组成,其中y1、y2、y3、y4分别为齿根和齿顶的最大修形量以及相应的修形区域长度,y5、y6、y7分别为齿向两端最大修形量和不修形区域长度,H、B为有效齿高、齿长. 本文中将旋转投影面沿齿高、齿长方向均匀划分为m×n网格点阵,由修形曲线计算网格节点的修形量δij(x,y),再通过3B样条对节点数据拟合得到光滑的修形曲面,其与理论齿面关系如下:
| $\left\{ \matrix{ x = \sqrt {R_x^2 + R_y^2} , \hfill \cr y = {R_2}. \hfill \cr} \right.$ |
式中Rx、Ry、Rz为理论齿面位矢坐标分量.
|
图 1 齿廓(左)、齿向(右)修形曲线 Figure 1 Profile (left) and longitudinal (right) modification curves |
本文采用理论齿面与修形曲面叠加的方式构造修形齿面,其位矢和法矢表示如下:
| $\eqalign{ & {R_{1r}}({u_1},{l_1}) = \delta (x,y){n_1}({u_1},{l_1}) + {R_1}({u_1},{l_1}), \cr & {n_{1r}} = ({{\partial {R_1}} \over {\partial {u_1}}} + {{\partial \delta } \over {\partial {u_1}}}{n_1} + {{\partial {n_1}} \over {\partial {u_1}}}\delta ) \times \cr & {{\partial {R_1}} \over {\partial {l_1}}} + {{\partial \delta } \over {\partial {l_1}}}{n_1} + {{\partial {n_1}} \over {\partial {l_1}}}\delta ). \cr} $ |
式中:R1、n1分别为理论齿面位矢和法矢;u1、l1分别为理论齿面参数;R1r、n1r分别为修形齿面位矢和法矢;δ为修形量.
2 优化模型 2.1 优化目标一,二(ALTE,齿面载荷)[7-9]通过TCA和LTCA可以得到接触线离散点位置坐标、曲率半径、载荷pij和轮齿法向位移Z(将Z转化为啮合线上位移,并用转角表示即为承载传动误差)等.其中,LTCA方法是一种基于齿面柔度矩阵的规划方法.齿轮啮合传动时,支撑轴的变形会影响齿面柔度矩阵,因此,本文基于有限元分析,将轴离散为若干单元来计算齿轮轮齿受到单位法向力作用时轴节点处的弹性变形,然后利用相关公式计算得到齿面结点的附加柔度,最后通过插值得到齿面离散点的附加柔度矩阵.
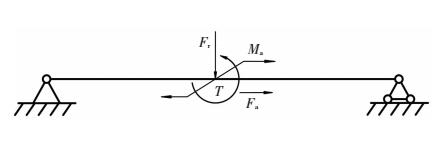
图 2所示为齿轮支承系统受力分析示意图,齿轮啮合力可以分解为端面法向力Fr和轴向力Fa,转移到轴上后,分别产生扭矩T和弯矩Ma.Fr和T引起轴系变形使齿面结点产生法向位移,是应考虑的重要因素,Fa和Ma引起轴系变形使齿面结点产生切向位移,其影响可以忽略.
|
图 2 齿轮支承系统受力分析 Figure 2 Force analysis of gear bearing system |
接触线上离散点载荷密度表示如下:
| $\left\{ \begin{align} & {{w}_{ij}}=\frac{2{{p}_{ij}}}{\left| {{L}_{i,j}}-{{L}_{i,j-1}} \right|+\left| {{L}_{i,j}}-{{L}_{i,j+1}} \right|},(1<j<n); \\ & {{w}_{i,j}}={{p}_{ij}}/{{L}_{i,j}},(j=1,n). \\ \end{align} \right.$ |
式中Li,j为第i条接触线上第j个点的位置坐标.
承载传动误差(LTE)可以表示如下:
| ${{z}_{e}}=\frac{3600\times 1800\times z}{\pi {{r}_{b}}\cos \beta }.$ |
则承载传动误差幅值(ALTE)为
| ${F_1} = \max \left\{ {{Z_e}} \right\} - \min \left\{ {{Z_e}} \right\}.$ |
式中rb、β分别为被动轮基圆半径和螺旋角.
本文采用接触线最大载荷密度最小来表述齿面载荷均匀程度最优,最大载荷密度为
| ${F_2} = \max \left\{ {{w_{ij}}} \right\}.$ |
计算齿面闪温的Blok基本公式[17]为
| ${\theta _{fla}} = {\mu _{my}}{X_a}{X_\beta }{X_M}{X_B}{{W_t^{0.75}V{'^{0.5}}} \over {a{'^{0.25}}}}.$ |
式中:θfla为啮合点处闪温;μmy为局部摩擦系数的平均值;Xα、Xβ和XM分别为啮合角系数、螺旋角系数和温升系数(本文中Xα和Xβ分别取为1,XM=50.0K·N-0.75·S0.5·m0.5.mm);XB为几何系数,可通过TCA求解;a′为啮合中心距;V′为节圆线速度.
接触线平均闪温为:
| ${F_3} = {{\sum\limits_{i = 1}^n {\theta _{fla}^i} } \over n}.$ |
式中:i表示接触线上的某个离散点,n表示接触线上离散点的数量.
本文参考了文献[18]中的混合弹流润滑摩擦系数回归方程,计算摩擦系数如下:
| $\eqalign{ & \left\{ \matrix{ \mu = 0.1 \sim 0.2,(\lambda \le 0.9); \hfill \cr \mu = 0.0981{1 \over {{\gamma ^{2.0755}}}},(0.9 < \lambda < 1.6); \hfill \cr \mu = 0.0472{1 \over {{\gamma ^{0.4309}}}},(1.6 \le \lambda \le 3); \hfill \cr \mu \approx 0.03,(\lambda > 3). \hfill \cr} \right. \cr & {h_{\min }} = 2.65{\alpha ^{0.54}}{({\eta _0}U)^{0.7}}{E^{ - 0.03}}{R^{0.43}}{W^{ - 0.13}}. \cr & \lambda = {{{h_{\min }}} \over {\sqrt {\mu _1^2 + \mu _2^2} }}. \cr} $ |
式中:λ为膜厚比,hmin为最小油膜厚度,μ1和μ2为齿面粗糙度,α为Barus黏压系数,η0为润滑油环境黏度,U为上下齿面啮合点平均速度,E′为综合弹性模量,R为综合曲率半径,W为载荷密度.
2.3 优化模型与优化过程优化目标函数表示为
| $\left\{ \begin{align} & F({{y}_{1}},{{y}_{2}},{{y}_{3}},{{y}_{4}},{{y}_{5}},{{y}_{6}},{{y}_{7}})= \\ & \min \left\{ {{a}_{1}}\times {{f}_{1}}+{{a}_{2}}\times {{f}_{2}}+{{a}_{3}}\times {{f}_{3}} \right\}; \\ & {{f}_{1}}={{F}_{1}}/{{F}_{10}},{{f}_{2}}={{F}_{2}}/{{F}_{20}},{{f}_{3}}={{F}_{3}}/{{F}_{30}}; \\ & {{q}_{\min }}\le {{y}_{1}},{{y}_{2}},{{y}_{5}},{{y}_{6}}\le {{q}_{\max }}; \\ & {{m}_{\min }}\le {{y}_{3}},{{y}_{4}}\le {{m}_{\max }}; \\ & {{l}_{\min }}\le {{y}_{7}}\le {{l}_{\max }}. \\ \end{align} \right.$ |
式中:yi(i=1~7)为优化变量(见图 1),ai(i=1~3)为权系数(∑ai=1,本文权系数均等),F10、F20、F30和F1、F2、F3为修形前和修形后的承载传动误差幅值、最大载荷密度、接触线平均闪温,qmin、qmax、mmin、mmax、lmin(取0.5B)、lmax(取0.8B)为修形参数约束量[1].
图 3为齿面修形优化计算流程图.

|
图 3 齿面修形优化计算流程 Figure 3 Calculation flowchart of tooth flank optimal modification |
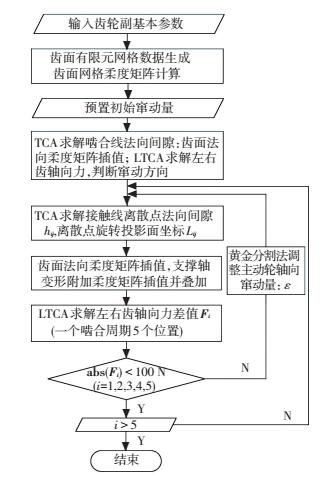
实际工程应用中误差不可避免,通常的应对措施是主动轮浮动安装,因此,在优化修形齿面的基础上,加入误差角,使主动轮沿轴向窜动,完成了有误差条件下的TCA和LTCA计算,流程图如图 4所示.
|
图 4 有误差角条件下的TCA和LTCA计算流程 Figure 4 Calculation flowchart of TCA and LTCA with misalignment errors |
齿轮副参数见表 1,负载扭矩2500Nm,输入转速8000r/min,齿轮本体温度为100℃,本体温度下润滑油黏度为5MPa·s,齿面粗糙度0.8μm.遗传算法种群数为50,进化30代,交叉概率为0.6,变异概率为0.1.修形参数优化结果见表 2.
| 表 1 齿轮副参数 Table 1 Parameters of gear pair |
| 表 2 修形参数优化结果 Table 2 Optimal results of tooth modification |
图 5(a)为主动轮三维有限元网格模型,图 6、图 7中“左"和“右"分别代表图 5(a)中的左边齿和右边齿;图 5(b) 为其优化修形曲线,齿廓修形左右完全一致,齿向修形关于人字齿退刀槽中心左右对称.

|
图 5 主动轮三维有限元模型和优化修形曲线 Figure 5 Three-dimensional finite element model of pinion and optimal modification curves |
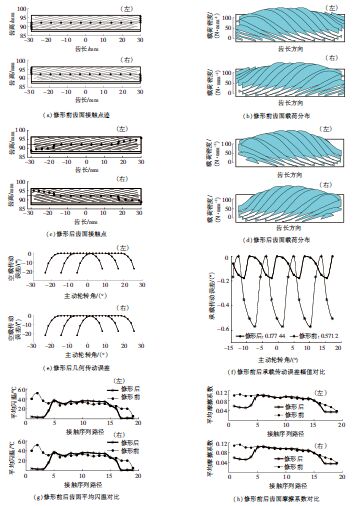
图 6(a)、(b)分别展示了修形前的齿面接触点迹和齿面载荷分布,由图中可以看出,进入和退出啮合时,齿面两齿侧存在边缘接触,且边缘接触线承担着较大载荷. 边缘接触往往会恶化齿轮传动,尤其是在高速转动下,会产生较大噪音和振动,进而使齿轮寿命受损;图 6(c)、(d)则分别为修形后的齿面接触点迹和齿面载荷分布,对比图 6(a)、(b)可以发现,修形后,在啮入区和啮出区,啮合点发生了转移,完全避免了边缘接触;图 6(e)为修形后的几何传动误差;图 6(f)给出了修形前后承载传动误差幅值的对比,可以看到,修形后承载传动误差幅值大幅下降. 这是因为轮齿啮合过程中,犹如承受动载荷的悬臂梁,单对齿啮合和多对齿啮合交替工作,啮合刚度周期性变化,从而导致轮齿弹性变形量周期性变化,承载传动误差幅值也随之周期性变化.齿面修形后,优良的修形参数能够保证啮合转换点之间尽可能平滑过渡,因此承载传动误差幅值大幅下降. 图 6(g)、(f)给出了修形前后齿面闪温对比和摩擦系数对比.从图 6(g)中可以看出,修形前啮入区为易发生胶合危险区域,工程设计中应注意. 综合对比图 6(g)、(f)可以发现,修形后啮入区和啮出区,摩擦系数降低明显,闪温大幅下降,其原因是修形后齿顶、齿根负载大幅下降,接触线上法向间隙增加,故油膜厚度增加,润滑状态改善,因此,摩擦系数下降,齿面闪温随之降低.
|
图 6 无安装误差修形前后计算结果对比 Figure 6 Comparisons of results between theoretical tooth and crowned tooth without misalignment errors |
当有安装误差时,主动轮轴向窜动,其过程实际就是左、右齿面间隙相互补偿的过程,进而实现左右齿面负载均衡. 图 7中的误差角γ=18.6″为未修形齿面极限误差角,从图 7(a)中可以看出,在此误差角下,接触点迹已经基本到达有效齿面的边界,当误差角进一步增大时,齿面将无法啮合.图 7(c)为此误差角下修形齿面接触点迹,对比修形前后接触点迹,可以充分证明齿面的优化修形有效降低了误差敏感性;图 7(b)、(d)、(e)、 (f)、(g)中的计算结果都是在γ=18.6″时,左右齿轴向力达到平衡后得到的.图 7(b)、(d)分别为修形前后,有误差角条件下的左右齿面载荷分布.从图中可以看出,轴向窜动对修形齿面和未修形齿面都能起到均布载荷的作用,但是对比图 7(b)、(d)仍然能够发现,修形后的齿面载荷分布更均匀,齿面修形与主动轮浮动安装相互补充,共同促进齿轮转动平稳;图 7(e)给出了修形前后,有误差角条件下,承载传动误差幅值对比,从图中可以看出,有误差角条件下,修形后的承载传动误差幅值依然大幅下降,对比结果进一步验证了优化参数对降低承载传动误差幅值的有效性;图 7(f)、(g)给出了误差条件下的齿面闪温对比和摩擦系数对比,结果表明:有误差条件下,修形齿面依然可以显著提高内啮合人字齿轮传动的抗胶合能力,进一步验证了优化修形参数是优良的.

|
图 7 误差角γ=18.6″时修形前后计算结果对比 Figure 7 Comparisons of results between theoretical tooth and crowned tooth with misalignment error γ=18.6″ |
1) 结合TCA、LTCA和遗传优化算法,得到了齿面的精确修形参数.优化后的啮合齿面仿真结果表明,修形后,承载传动误差幅值大幅下降,胶合危险区域(啮入区)闪温明显降低,同时有效避免了边缘接触,使得齿面受载均匀;
2) 当齿轮轴线由于受载变形、制造误差或安装误差产生偏斜时,通过三维修形可以有效地减小齿轮啮合对误差的敏感性,避免产生过大的偏载;
3) 当齿轮轴线发生偏斜时,主动轮轴向窜动,使左右齿面间隙相互补偿,齿面修形与主动轮浮动安装相互补充,使得左右齿面载荷逐步趋于相等,保证了齿轮啮合过程的平稳;
4) 本文提出的优化设计方法考虑了弹性支撑轴变形的影响,仿真优化模型更进一步贴近齿轮实际工作条件,是高速齿轮修形设计的有效手段.
| [1] |
詹安东, 王树人, 唐树为. 高速齿轮齿部修形技术研究[J].
机械设计, 2000, 8 (8) : 8-10.
ZHAN Andong, WANG Shuren, TANG Shuwei. A study on tooth dressing technique of high speed gears[J]. Journal of Machine Design, 2000, 8 (8) : 8-10. DOI: 10.3969/j.issn.1001-2354.2000.08.003 |
| [2] |
成国玉. 高速齿轮的修形[J].
现代冶金, 2004, 32 (4) : 37-40.
CHENG Guoyu. Tooth correction of high speed gears[J]. Journal of Modern Metallurgy, 2004, 32 (4) : 37-40. DOI: 10.3969/j.issn.1005-6068.2004.04.015 |
| [3] |
杨欣荣. 高速齿轮修形技术在大功率新型高速齿轮箱上的应用[J].
机械制造与自动化, 2005 (3) : 44-47.
YANG Xinrong. High-speed tooth relief technique applied on the large power and high-speed modern gearbox[J]. Journal of Machine Building & Automation, 2005 (3) : 44-47. DOI: 10.3969/j.issn.1671-5276.2005.03.016 |
| [4] | LITVIN F L, FUENTES A, GONZALEZ-PEREZ I, et al. Modified involute helical gears: computerized design, simulation of meshing and stress analysis[J]. Comput Methods Appl Mech Engrg, 2003, 192 (33/34) : 3619-3655. DOI: 10.1016/S0045-7825(03)00367-0 |
| [5] | LITVIN F L, LU Jian, TOWNSEND D P, et al. Computerized simulation of meshing of conventional helical involute gears and modification of geometry[J]. Mechanism and Machine Theory, 1999, 34 (2) : 123-147. DOI: 10.1016/S0094-114X(98)00013-5 |
| [6] | LITVIN F L, FAN Qi, VECCHIATO D, et al. Computerized generation and simulation of meshing of modified spur and helical gears manufactured by shaving[J]. Comput Methods Appl Mech Engrg, 2001, 190 (39) : 5037-5056. DOI: 10.1016/S0045-7825(00)00362-5 |
| [7] |
方宗德. 修形斜齿轮的轮齿接触分析[J].
航空动力学报, 1997, 12 (3) : 247-250.
FANG Zongde. Tooth contact analysis of modified helical gears[J]. Journal of Aerospace Power, 1997, 12 (3) : 247-250. |
| [8] |
方宗德. 修形斜齿轮的承载接触分析[J].
航空动力学报, 1997, 12 (3) : 252-254.
FANG Zongde. Loaded tooth contact analysis of modified helical gears[J]. Journal of Aerospace Power, 1997, 12 (3) : 252-254. |
| [9] |
方宗德. 斜齿轮齿面柔度矩阵与修形的有限元计算[J].
航空动力学报, 1994, 9 (3) : 242-244.
FANG Zongde. Calculation on flexibility matrix and modification of helical gears by FEM[J]. Journal of Aerospace Power, 1994, 9 (3) : 242-244. |
| [10] |
王成, 方宗德, 贾海涛, 等. 人字齿轮修形优化设计[J].
航空动力学报, 2009, 24 (6) : 1433-1436.
WANG Cheng, FANG Zongde, JIA Haitao, et al. Modification optimization of double helical gears[J]. Journal of Aerospace Power, 2009, 24 (6) : 1433-1436. |
| [11] |
蒋进科, 方宗德, 苏进展. 宽斜齿轮多目标修形优化设计[J].
西安交通大学学报, 2014, 48 (8) : 91-97.
JIANG Jinke, FANG Zongde, SU Jinzhan. Multi-objective optimal and modified design for wide helical gear[J]. Journal of Xi'an Jiaotong University, 2014, 48 (8) : 91-97. DOI: 10.7652/xjtuxb201408016 |
| [12] |
唐进元, 陈兴明, 罗才旺. 考虑齿向修形与安装误差的圆柱齿轮接触分析[J].
中南大学学报, 2012, 43 (5) : 1703-1709.
TANG Jinyuan, CHEN Xingming, LUO Caiwang. Contact analysis of spur gears based on longitudinal modification and alignment errors[J]. Journal of Central South University, 2012, 43 (5) : 1703-1709. |
| [13] |
李杰. 齿轮传动涡轮风扇(GTF)发动机先进技术综述[J].
航空发动机, 2009, 35 (4) : 54-57.
LI Jie. Overview of advanced technology for geared turbofan engine (GTF)[J]. Journal of Aeroengine, 2009, 35 (4) : 54-57. DOI: 10.3969/j.issn.1672-3147.2009.04.014 |
| [14] |
陈聪慧, 信琦. 风扇齿轮驱动系统的概念设计[J].
航空科学技术, 2011 (4) : 8-11.
CHEN Conghui, XIN Qi. Conceptual design of fan gear drive system[J]. Journal of Aeronautical Science & Technology, 2011 (4) : 8-11. DOI: 10.3969/j.issn.1007-5453.2011.04.003 |
| [15] |
张德志, 张锦绣, 王凤. 齿轮驱动涡扇发动机结构设计特点分析[J].
航空发动机, 2011, 37 (4) : 1-4.
ZHANG Dezhi, ZHANG Jinxiu, WANG Feng. Analysis of structural design characteristics for geared turbofan engine[J]. Journal of Aeroengine, 2011, 37 (4) : 1-4. DOI: 10.3969/j.issn.1672-3147.2011.04.002 |
| [16] |
候明曦, 李锦花, 张茂强, 等. GTF发动机行星齿轮传动系统设计技术研究[J].
航空发动机, 2014, 40 (2) : 61-64.
HOU Mingxi, LI Jinhua, ZHANG Maoqiang. Research on design technology of planetary gear system for geared turbofan engine[J]. Journal of Aeroengine, 2014, 40 (2) : 61-64. |
| [17] | Ministry of aviation industry of PRC. HB/Z 84[J]. Beijing: Standards Press of China, 1986 : 61-64. |
| [18] |
高创宽.渐开线齿轮传动的混合弹流润滑研究[D].太原:太原理工大学, 2005.
GAO Chuangkuan. Study of involute gearing mixed elastohydrody-namic lubrication [D]. Taiyuan:Taiyuan University of Technology, 2005. http://www.cqvip.com/QK/92228A/201311/47860263.html |
 2017, Vol. 49
2017, Vol. 49


