2. 低品位能源利用技术及系统教育部重点实验室(重庆大学),重庆 400044
2. Key Laboratory ofLow-grade Energy Utilization Technologies and Systems(Chongqing University),Ministry of Education,Chongqing 400044, China
圆柱绕流是流体力学研究中经典的自然现象,同时也是流场配置最为基本的钝体绕流形式.在绕流现象发生时,圆柱会在交替的旋涡脱落作用下受到周期性激振力从而发生祸激振动(vortex-induced vibration,简称VIV)[1-3].若钝体的涡激振动频率与其固有频率较为接近,则振动频率会被锁定,当继续提高流速时,圆柱振幅增大而振动频率基本保持稳定,此为同步性(锁定)现象.Bearman等[4]和Feng[5]通过风洞实验和水槽圆柱绕流实验研究了圆柱绕流的同步性现象.其中Bearman发现同步性现象按其振幅大小及频率锁定情况分为初始分支、上部分支和下部分支3个阶段;Feng首次在风洞实验观测到了上部分支消失的现象.在工程应用中,“锁振"往往被作为有害的自然现象需要预测和消除,近年来却出现了利用锁振现象进行能量收集的研究工作[6-9].
Zdravkovich[10]定义了光滑圆柱绕流在不同雷诺数(Re=ud/v,u为来流速度,l为圆柱直径,v为流体运动黏度)下的15个分支,并且将亚临界区域划分为5个区域:基于剪切层过渡理论的有3个区域,分别是自由剪切层过渡区旋涡发展(TrSL1/Transition of shear layer1,300~500, Re<1×103~2×103)、自由剪切层过渡旋涡(TrSL2,1×103〜2×103<Re<2×104〜4×104)和完全湍流剪切层(TrSL3,2×104~4×104<Re<1×105~2×105).在TrSL2内,流动剪切层开始从层流过渡到湍流.Williamson等[11]综述了近十年来低雷诺数圆柱绕流涡激振动的主要成果.Govardhan等[12]发现尺Re在4500左右时,圆柱涡激振动的振幅是办的函数.Khalak等[13]发现在Re办为5×103〜8×103范围内系统的升力系数随雷诺数提高而提高,并发现在同步现象产生时,出现两个或3个分支与阻尼参数$\alpha =(m*+Ca)\xi (\xi $是量纲一阻尼比,Ca是附加质量系数,圆柱Ca=1)有重要关系.Govardhan发现:是否出现两个分支除了受α影响之外,还受到雷诺数范围的影响.然而,其计算Re值较低,不能用于判定高雷诺数下是否出现两分支.Vikestad等[14]在Re=1×105时得到了1.13倍圆柱直径振幅.Xu等[15]在雷诺数为3×104〜2.5×105时得到了最大值为1.9倍圆柱直径的振幅.Bernitsas等w在VIVACE平台下加人PTC(passive turbulence control)后在Re=8×104〜 1.32×105内得出了大约为2倍圆柱直径的振幅.Griffin等[17]在实验中发现涡激振动振幅峰值与流体的黏度和密度等参数有关.Sarpkaya[18]试图找出涡激振动振幅比与Skop-Griffin参数的指数关系,但忽略了雷诺数的重要影响.加州理工学院和康奈尔大学的学者发现在低雷诺数条件下涡激振动的振动峰值是雷诺数的函数.Goverdhan等[12]在TrSL2下提出了振动峰值A*与参数的半经验关系式:
| ${{A}^{*}}=(1-1.12\alpha +0.30{{\alpha }^{2}})lo{{g}_{10}}(0.41R{{e}^{0.36}}).$ |
目前,针对高雷诺数区域如TrSL3区域内雷诺数与阻尼参数α对涡激振动系统影响的研究仍较少.本文对TrSL3区域中不同组阻尼参数α的圆柱绕流涡激振动问题,应用雷诺平均法(RANS)结合Spalart-Allmaras—方程湍流模型描述绕流外部流场,采用二阶范德波尔方程求解单自由度质量-弹簧-阻尼(M-K-C)振动响应.着重研究了高雷诺数下涡激振动出现不同分支与振幅峰值的关键影响因素,并在此基础上分析不同雷诺数和不同参数对涡激振动的振幅、频率、涡脱模式等重要特征的影响.研究结果为完全湍流剪切层下的圆柱绕流流致振动的机理研究提供理论基础,并对工程中利用涡激振动现象的能量收集工作具有一定指导意义.
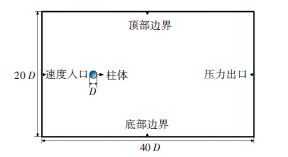
1 物理模型 1.1 流场计算域及边界条件流固耦合计算区域包括5个边界条件:速度进口、压力出口、顶部边界、底部边界和圆柱外表壁,如图 1所示.计算区域为40D×20D,其中D为圆柱直径,圆柱体位于距离进口位置10D处.速度在进口为固定值U,压力梯度为零.压力出口设为充分发展流动,速度梯度为零,出口背压值Pb=0.上下壁面设为零速度压力梯度.柱体外表壁设为滑移壁面边界条件,速度为滑移壁面速度,压力梯度为零.
|
图 1 流场计算域 Figure 1 Flow field calculation domain |
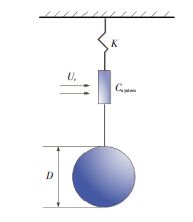
假定弹性支撑圆柱为单自由度质量-弹簧-阻尼系统(见图 2),其振动方向垂直于来流速度方向.来流速度取量纲一的折减速度${{U}_{r}}=U/{{\omega }_{n}}\bullet D$,其中${{\omega }_{n}}$为圆柱固有频率.柱体被支撑在弹性系数为K的弹簧上,系统总阻尼为${{C}_{\text{System}}}$.
|
图 2 单自由度振动系统 Figure 2 Single degree⁃of⁃freedom vibration system |
在流固耦合计算中,动网格的处理是影响计算精准度的重要因素.为保证在物面流动变量变化梯度大的位置获得高分辨率网格,对圆柱近壁面处网格进行加密,在远离圆柱表面后逐渐稀疏.传统动网格方法会导致网格产生挤压变形,当挤压过大时,网格甚至会产生折叠或畸变而导致计算终止,大大影响计算效率和计算精度.本文网格如图 3,图 3(a)为近壁面网格示意图,图 3(b)〜(d)为圆柱在静止、振动最大和最小值时的位置.采用拓扑动网格技术,在OpenFOAM动网格子程序中使控制子块(2D×2D),子块内网格随柱体壁面整体运动,从而避免因网格扭曲而引起的计算误差.湍流计算是典型的非稳态计算问题,在数值计算中消耗的资源较大,因此在保证网格的计算精度时应保证网格数不能过多.为此,文中进行了网格无关性验证,采用粗网格、细网格、极细网格3组疏密程度不同的网格参数在办Re=2×104下对D=0.0889m圆柱绕流进行计算,计算结果见表 1.由表 1中可见,3组网格具有无关性,本文在保证计算精度的情况下选定细网格.

|
图 3 动网格示意图 Figure 3 The moving grid |
| 表 1 网格无关性验证(Re=2×104) Table 1 Verification of independence of the grids |
针对高雷诺数圆柱绕流的流场计算,建立不可压RANS方程:
| $\begin{align} & \partial {{U}_{i}}/\partial {{x}_{i}}=0,\\ & \frac{\partial U}{\partial t}+\frac{\partial }{\partial {{x}_{i}}}\left( {{U}_{\text{i}}}{{U}_{j}} \right)=-\frac{1}{\rho }\frac{\partial }{\partial {{x}_{i}}}+\frac{\partial }{\partial {{x}_{j}}}(2v{{S}_{ij}}-\overline{{{u}_{i}}'{{u}_{j}}'}). \\ \end{align}$ |
式中:v为运动黏度,ρ为流体密度,Sij.为应变率张量,定义
| ${{S}_{ij}}=\frac{1}{2}(\frac{\partial {{U}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{U}_{j}}}{\partial {{x}_{i}}}).$ |
其中,Ui是平均速度,ui'是脉动速度.
在雷诺平均(RANS)法中定义雷诺应力张量τij为
| ${\tau _{ij}} = - \rho \overline {{u_i}'{u_j}'} ,$ |
由Boussinesq涡黏假定,忽略湍流脉动能,建立雷诺应力与平均速度梯度的关系式:
| $ - \rho \overline {{u_i}'{u_j}'} = 2{\mu _t}{S_{ij}}.$ |
式中μt是湍流黏度.
本文湍流模型采用文献[19]中的Spalart-Allmaras—方程揣流模型.Spalart-Allmaras揣流模型主要针对壁面束缚流动,其特点是相较于双方程模型计算量小、稳定性好,而相较于其他一方程模型,其当地型特点可使其在流场中任一位置的方程不依赖于其他位置的解.因此在湍流流场中能够避免其他复杂处理,从而保证计算稳定性.
2.2 柱体振动方程单自由度质量-弹簧-阻尼振动系统的二阶范德波尔万程:
| $m\ddot{y}+{{c}_{system}}\dot{y}+ky={{F}_{y}}(t).$ |
式中:m为系统总质量,Fy(t)为柱体垂直方向升力,可由柱体表面压力和黏性力积分得到,圆柱振动的运动速度和振幅采用二阶隐式积分法求解.
本文的参数和工况选取如表 2所示.
| 表 2 单自由度涡激振动系统参数 Table 2 Parameters of the SDOF VIV system |
表 2中质量比的定义为
| $m*=m/{{m}_{a}},{{m}_{a}}={{C}_{a}}{{\rho }_{f}}\pi {{D}^{2}}/4$ |
其中:ma是柱体排开的流体质量,ρf是流体的密度.
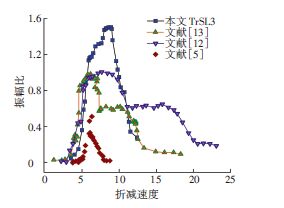
3 结果与讨论 3.1 雷诺数对涡激振动性能的影响本文所采用流固耦合求解器已在文献[20]中得以有效验证.图 4对比了在相同折减速度下,TrSL3与Khalak[13],Govardhan[12]和Feng[5]等的低雷诺数计算结果.由图 4可知,尽管本文参数a比khalak[13]高出20倍(α=0.3874),但在TrSL3区域下的同步区域计算结果较为接近,当前计算的锁定区域宽度几乎与Khalak[13]的上支与下支宽度总和相同.这是由于TrSL3中较高的流场激振力系数所导致.在Govardhan等[12]的实验中其参数α小于本文,但当前TrSL3计算所得振幅可达其1.5倍,且同 步区域与其上支区域的范围较为吻合.
|
图 4 较低雷诺数与本文高雷诺数高阻尼参数计算结果对比 Figure 4 Comparison of computational results between present high and lower Reynolds numbers |
在Feng[5]的实验中,质量比数值较高,参数α约为本文的1.4倍,但由于其采用的是低雷诺数工况,因此振幅较小,最大振幅值仅为A=0.55D.当前振幅计算结果的变化趋势与Feng[5]的实验结果较为吻合,但是本文计算结果中主要部分为上部分支,而Feng[5]的实验结果主要为下部分支.
产生这种现象的主要原因是当α提高时,尾迹中部端面压力的相关性减少,从而会产生下部分支延长的现象.因此,在雷诺数较高的TrSL3区域下,即使质量/阻尼比参数α较高,也可捕捉到较高振幅.
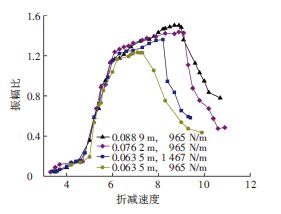
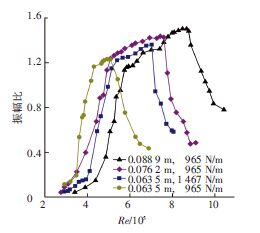
图 5、6为TrSL3区域下不同直径D和弹性系数k的圆柱量纲一的涡激振动振幅A/D随折减速度Ur和雷诺数变化的结果.从图中可以看出:在折减速度Ur=7.5时,存在一个转折点;当Ur<7.5时,4种振动系统振幅均随着折减速度的增大呈现递增趋势,振幅曲线处于锁振的初始或上支阶段,此时雷诺数对振动振幅没有明显影响.
|
图 5 TrSL3 区域下同步区域振幅随折减速度的变化 Figure 5 Variations of vibrational amplitudes with reduced velocities under TrSL3 |
而当Ur达到7.5时,圆柱1的振幅曲线开始下降并进人下支阶段;继续提升Ur时,圆柱2与圆柱3的振幅曲线也开始进人下支阶段,圆柱4的振幅曲 线幅值随着雷诺数的增大而持续升高,最后进人下支.这是因为D=0.0635m圆柱固有频率相对较低,当Ur=7.5时,振动频率逐渐失去与尾迹旋涡的锁定,振幅随流速增加开始下降,并且由上支过渡到 下支阶段.
当提高D=0.0635m圆柱的弹性系数时,在相同折减速度下,雷诺数与固有频率同时提高,此时的上支范围增大.
当D=0.0762m时,在相同折减速度下,雷诺数高于0.0635m的工况,振动振幅高于0.0635m圆柱且同步区域更宽.D=0.0889m圆柱振荡振幅幅值沿上支逐渐增大,振荡振幅的峰值可达A=1.5从D=0.0635m时振幅幅值的增长曲线先增大后减小,且振幅曲线的同步性区域增大.
综上可见,在TrSL3区域下,雷诺数对于同步现象的振幅和范围大小具有决定性作用.
图 6表示TrSL3区域下,不同圆柱直径、不同弹性系数下的圆柱绕流涡激振动随雷诺数变化的结果.从中可以得出,圆柱尺寸和来流速度范围相同时,雷诺数对振动幅值和同步区域范围的提高影响明显.
|
图 6 TrSL3 区域下同步区域振幅随雷诺数的变化 Figure 6 Variations of vibrational amplitudes with Reynolds numbers under TrSL3 |
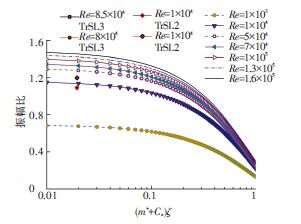
将本文TrSL2和TrSL3高质量/阻尼比参数α的计算结果与半经验公式(1)得出的曲线在Griffin图谱中进行对比,结果见图 7.由图 7可知,在较低雷诺数,TrSL2计算结果与公式1符合较好;但在高雷诺数,TrSL3计算结果要高于半经验计算值,从而再次说明雷诺数范围的改变对涡激振动系统的振幅具有决定性影响.
|
图 7 TrSL3 与半经验公式对比 Figure 7 Comprisons between semi⁃emprical formulas and TrSL3 |
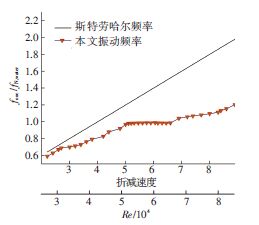
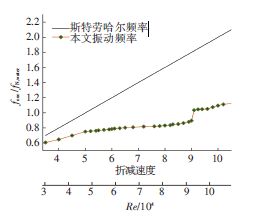
图 8、图 9为不同折减速度和雷诺数下两种不同直径圆柱的量纲一涡激振动频率比fosc/fN,water,其中直线表示Strouhal频率,即固定绕流时的量纲一旋涡脱落频率.
|
图 8 D=0.0635m,K=965N/m圆柱VIV频率比变化 Figure 8 Frequency ratios of VIV for cylinder of D=0.0635m, K=965N/m |
|
图 9 D=0.0889m,K=965N/m圆柱VIV频率比变化 Figure 9 Frequency ratios of VIV for cylinder of D=0.0889m,K=965N/m |
D=0.0635m圆柱的同步区域在Ur=6.0〜7.5时进人上支,此时振动频率较为稳定,频率比fosc/fN,water保持在1附近;当继续增大来流速度后,振动振幅减小,振动频率会出现“跳跃"而后逐渐增大,此时振幅曲线进入下支.D=0.0889m的柱体在折减速度提升至Ur=6.0附近时,振幅曲线即产生“跳跃",并开始从上支直接过渡到下支.这是由于雷诺数的提升对同步性区域的上支范围的增大有增强作用,且上支的振动幅值会随着雷诺数的增大而明显提高.
3.3 雷诺数对旋涡尾迹结构的影响图 10中包括两组不同计算结果.第一组为Govardhan等[12]在低雷诺数下和低阻尼参数α工况下的量纲一振幅计算结果,第二组为本文D=0.0889m,k=965N/m圆柱在高雷诺数和高阻尼参数α工况下,量纲一振幅的计算结果.图中横坐标采用Williamson等[21]提出的真实折减速度,其定义式为:$U{{*}_{real}}=(U*/f*){{S}_{t}}$,St取0.18.通过W-R图谱[21]观察第1组数据可知,初始支穿过2S(S代表单个旋涡)模态区域.而观察第2组数据可知,TrSL3在当U∗real较小时,近壁面处圆柱涡激振动受雷诺数影响较为薄弱,此时旋涡脱落较为规律,呈现2S模式.并在相较于Govardhan[12]较高的U∗real时才开始进入同步性区域,上支大多数集中在2P(P代表旋涡对)模态中.此时观察旋涡脱落云图 11可以捕捉到2P模态.当继续提升U∗real,振幅曲线进入同步区域时,近壁面处波动升力较强并开始产生二次涡.

|
图 10 Williamson⁃Roshko图谱中本文高质量阻尼比在高雷诺数下的振幅响应图 Figure 10 Vibrational amplitudes under high Reynolds numberswith present parameters of mass and damping ratio inWilliamson⁃Roshko map |

|
图 11 TrSL3 同步区域内的尾迹涡脱模式图(U∗real=1.2) Figure 11 Vortex shedding patterns under the TrSL3 synchronizationalregions(U∗real=1.2) |
1) 在TrSL3下获得圆柱振动的最大振幅,并与文献中TrSL2下的实验及Griffin图谱中的半经验拟合公式进行了对比,结果表明:在相同的折减速度范围下,提高雷诺数时,圆柱振动振幅会显著增大,同时振幅曲线的同步区域的范围也会增大.在湍流度充分发展的TrSL3下,雷诺数对涡激振动的振幅和同步区域的范围有着决定性的作用.
2) 在TrSL3区域中,当提高质量阻尼比参数时,涡激振动同步区域的上部分支消失,振幅曲线直接由初始分支过渡到下部分支,振动频率出现“阶跃"现象.
3) 在TrSL3区域下,当真实折减速度达到一定数值时,尾迹旋涡脱落模式开始由2S转换为2P模式.
| [1] |
曹淑刚, 黄维平, 顾恩凯. 考虑流固耦合的弹性圆柱体涡激振动研究[J].
振动与冲击, 2015, 34 (1) : 58-62.
CAO Shugang, HUANG Weiping, GU Enkai. Study on vortex-induced vibration of an elastic cylinder considering fluid-structure interaction[J]. Journal of vibration and shock, 2015, 34 (1) : 58-62. DOI: 10.13465/j.cnki.jvs.2015.01.012 |
| [2] |
关德宝, 黄维平, 宋虹. 串列圆柱体尾流和尾涡耦合振动试验研究[J].
振动与冲击, 2014, 33 (22) : 26-29.
GUAN Debao, HUANG Weiping, SONG Hong. Experimental investigation of wake flow and wave-vortex coupling induced vibration of two tandem and cylinders[J]. Journal of vibration and shock, 2014, 33 (22) : 26-29. DOI: 10.13465/j.cnki.jvs.2014.22.005 |
| [3] |
唐友刚, 樊娟娟, 张杰. 高雷诺数下圆柱顺流向和横向涡激振动分析[J].
振动与冲击, 2013, 32 (13) : 88-92.
TANG Yougang, FAN Juanjuan, ZHANG Jie. Analysis of in line and transverse vortex-induced vibration for a circular cylinder at high reynolds number[J]. Journal of vibration and shock, 2013, 32 (13) : 88-92. DOI: 10.13465/j.cnki.jvs.2013.13.012 |
| [4] | ANAGNOSTOPOULOS P, BEARMAN P W. Response characteristics of a vortex-excited cylinder at low Reynolds numbers[J]. Journal of Fluids and Structures, 1992, 6 (1) : 39-50. DOI: 10.1016/0889-9746(92)90054-7 |
| [5] | FENG C C. The measurement of vortex-induced effects in flow past stationary and oscillating circular and d-section cylinders[D]. Vancouver: University of British Columbia,1968. DOI:10.14288/1.0104049. http://cn.bing.com/academic/profile?id=e0f8844c11203eeb04f9a2dd2917137e&encoded=0&v=paper_preview&mkt=zh-cn |
| [6] | DAI H L, ABDELKEFI A, WANG L. Piezoelectric energy harvesting from concurrent vortex-induced vibrations and base excitations[J]. Nonlinear Dynamics, 2014, 77 (3) : 967-981. DOI: 10.1007/s11071-014-1355-8 |
| [7] | MICHELIN S, DOAR D. Energy harvesting efficiency of piezoelectric flags in axial flows[J]. Journal of Fluid Mechanics, 2013, 714 (1) : 489-504. DOI: 10.1017/jfm.2012.494 |
| [8] |
罗竹梅, 张立翔. 影响从涡激振动中获取能量的参数研究[J].
振动与冲击, 2014, 33 (9) : 12-15.
LUO Zhumei, ZHANG Lixiang. The influence of parameters on harvesting energy from vortex-induced vibration[J]. Journal of vibration and shock, 2014, 33 (9) : 12-15. DOI: 10.13465/j.cnki.jvs.2014.09.003 |
| [9] | GAO X T, WEI H S, WAN Y S. Flow energy harvesting using piezoelectric cantilevers with cylindrical extension[J]. IEEE Transactions on Industrial Electronics, 2013, 60 (3) : 1116-1118. DOI: 10.1109/TIE.2012.2187413 |
| [10] | ZDRAVKOVICH M M. Flow around circular cylinders: Volume 1[M]. $S.L.$: Oxford Science Publications, 1997 : 37 -44. |
| [11] | GOVARDHAN R, WILLIAMSON C H K. Modes of vortex formation and frequency response of a freely vibrating cylinder[J]. Journal of Fluid Mechanics, 2000, 420 : 85-130. DOI: 10.1017/S0022112000001233 |
| [12] | GOVARDHAN R N, WILLIAMSON C H K. Defining the'modified Griffin plot’in vortex-induced vibration: revealing the effect of Reynolds number using controlled damping[J]. Journal of Fluid Mechanics, 2006, 561 (9) : 147-180. |
| [13] | KHALAK A, WILLIAMSON C H K. Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping[J]. Journal of Fluids and Structures, 1999, 13 (7/8) : 813-851. DOI: 10.1006/jfls.1999.0236 |
| [14] | VIKESTAD K, VANDIVER J K, LARSEN C M. Added mass and oscillation frequency for a circular cylinder subjected to vortex-induced vibrations and external disturbance[J]. Journal of Fluids and Structures, 2000, 14 (7) : 1071-1088. DOI: 10.1006/jfls.2000.0308 |
| [15] | XU J, SPENCER D, GARDNER A. Wake fields behind risers undergoing vortex-induced vibration[C]// ASME International Conference on Offshore Mechanics & Arctic Engineering. $S. l.$: ASME, 2008: 539-546. DOI:10.1115/OMAE2008-57068. http://cn.bing.com/academic/profile?id=9a28892865a946b051ac5755642970cb&encoded=0&v=paper_preview&mkt=zh-cn |
| [16] | LEE J H, BERNITSAS M M. High-damping, high-Reynolds VIV tests for energy harnessing using the VIVACE converter[J]. Ocean Engineering, 2011, 38 (16) : 1697-1712. DOI: 10.1016/j.oceaneng.2011.06.007 |
| [17] | GRIFFIN O M, VANDIVER J K. Vortex-induced strumming vibrations of marine cables with attached masses[J]. Journal of Energy Resources Technology-Transactions of the Asme, 1984, 106 (4) : 458-465. DOI: 10.1115/1.3231106 |
| [18] | SARPKAYA T. Hydrodynamic damping and quasi-coherent structures at large Stokes numbers[J]. Journal of Fluids and Structures, 2001, 15 (7) : 909-928. DOI: 10.1006/jfls.2001.0384 |
| [19] | DING L, BERNITSAS M M, KIM E S. 2-D URANS vs. experiments of flow induced motions of two circular cylinders in tandem with passive turbulence control for 30 000≤Re≤ 105 000[J]. Ocean Engineering, 2013 (72) : 429-440. DOI: 10.1016/j.oceaneng.2013.06.005 |
| [20] |
王军雷, 冉景煜, 张智恩, 等. 外界载荷对圆柱涡激振动能量转换的影响[J].
浙江大学学报(工学版), 2015, 49 (6) : 1093-1100.
WANG Junlei, RAN Jingyu, ZHANG Zhien. Effects of external load on energy conversion of vortex-induced vibrating cylinder[J]. Journal of Zhejiang University (Engineering Science), 2015, 49 (6) : 1093-1100. DOI: 10.3785/j.issn.1008-973X.2015.06.013 |
| [21] | WILLIAMSON C H K, ROSHKO A. Vortex formation in the wake of an oscillating cylinder[J]. Journal of fluids and structures, 1988, 2 (4) : 355-381. DOI: 10.1016/S0889-9746(88)90058-8 |
 2017, Vol. 49
2017, Vol. 49


