2. 航天飞行动力学技术国家级重点实验室(西北工业大学),西安 710072
2. State Key Laboratory of Aerospace Flight Dynamics(Northwestern Polytechnical University), Xi'an 710072, China
航天器轨道动力学与控制是航天技术工程中的重要组成部分.在对航天器的轨道机动进行优化设计时,通常将地球视为质点模型,航天器在中心引力场中进行机动变轨.然而在实际飞行中,航天器受到空间环境各种摄动因素的影响,其轨道要素发生变化.这些摄动力包括地球形状非球形的附加引力、大气阻力、日月引力、太阳光压等摄动力,其中地球扁率的J2项摄动远大于其他摄动因素,是引起航天器轨道变化的主要因素.
考虑J2项摄动的轨道优化问题,逐渐成为国内外学者的研究热点.文献[1]提出了基于开普勒二体运动推算地球引力模型J2摄动的间接补偿的方法; 对于采用脉冲推进的航天器,文献[2]在二体模型的基础上,对J2项摄动下的Lambert问题进行求解;文献[3]阐述了J2摄动的原因和模型,并对J2摄动的补偿算法进行研究;文献[4]通过理论分析确定两次脉冲假设下,考虑地球扁率的机动轨道在地心转移角接近π时对边界条件比较敏感的原因,并提出相应解决办法;文献[5]研究了在地球扁率影响下,固定时间两异面椭圆轨道间的多冲量最优交会控制问题;文献[6]针对J2项摄动影响下的多脉冲最优机动的卫星编队构型的建立和重构,提出了一种高效的在线计算方法.
与脉冲推进相比,小推力发动机具有比冲大、控制精度高等优点,利用小推力推进进行轨道机动是未来发展趋势.由于小推力发动机推力小,持续时间长,其轨道优化存在较大困难.对于小推力转移轨道优化,该过程属于转移轨道设计过程中的局部优化,优化方法主要可以分为间接法、直接法和混合法,其中间接法通过推导最优性一阶必要条件,得到局部最优解,其最优性优于混合法和直接法,文献[7]对小推力转移轨道的优化方法进行了详细的比较说明.文献[8]通过间接法对深空探测中的燃料最优小推力转移轨道进行研究,利用粒子群算法选取初值,结合同伦算法和开关函数检测法克服Bang-Bang控制的困难.文献[9]对转移轨道的推力大小同伦过程进行研究,提出2次同伦方法,克服同伦过程不连续的问题.对于考虑J2项的小推力转移.文献[10]对J2项摄动影响下,卫星编队重构的燃料最优机动策略进行研究,通过Gauss伪谱法进行离散,并利用非线性优化软件TOMLAB/SNOPT进行优化.文献[11]利用直接法研究了考虑J2项摄动的平面内最小时间的小推力转移.文献[12]对于推力加速度和J2项摄动加速度为同一量级的情况下,将小推力和地球扁率视为摄动力,研究了小推力和J2项摄动对轨道要素的影响.文献[13]以时间最短为性能指标,推力幅值恒定,利用Gauss伪谱法对摄动情况下的有限推力转移轨道和交会联合优化问题进行了研究.
本文针对发动机推力远小于J2项摄动力的燃料最优转移轨道问题,基于间接法和同伦法对其进行研究,通过引入多个同伦参数,分别对动力学模型、推力大小和性能指标进行同伦.首先采用“线性引力”假设,选取性能指标为能量最优,求解较大推力的转移轨道;对动力学模型进行同伦,得到考虑J2摄动的较大推力能量最优转移轨道;然后对推力大小进行同伦,得到小推力的能量最优转移轨道;最后对性能指标进行同伦,克服Bang-Bang控制不连续的问题,最终得到所需的燃料最优转移轨道.
1 考虑J2项摄动的动力学模型对于在近地轨道运行的航天器,其受到的地球扁率所引起的J2项摄动力比三体引力、太阳光压等其他摄动力大数个量级,是主要的摄动力,在此仅考虑航天器受到地球中心引力和J2项摄动的影响.此时,航天器的动力学方程为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot r}} = \mathit{\boldsymbol{v}},\\ \mathit{\boldsymbol{\dot v}} = - \frac{\mu }{{{\mathit{\boldsymbol{r}}^3}}}\mathit{\boldsymbol{r}} + {\mathit{\boldsymbol{a}}_{{\rm{J}}2}} + \frac{{{T_{\max }}u}}{m}\mathit{\boldsymbol{\alpha }},\\ \dot m = - \frac{{{T_{\max }}u}}{{{I_{{\rm{sp}}}}{g_0}}}. \end{array} \right. $ | (1) |
式中:r、v分别为航天器在惯性坐标系中的位置和速度矢量;m为航天器的实时质量;μ为中心天体的引力系数;Tmax为发动机推力最大幅值;Isp为发动机比冲;g0为地球海平面的平均重力加速度,其值为9.806 65 m/s2;u为发动机工作时的推力大小,取值范围为u∈[0, 1];α=[αx, αy, αz]T为发动机单位推力在3个坐标轴上的分量,满足‖α‖=1,aJ2为地球J2项摄动所引起的加速度,其表达式为
| $ \left\{ \begin{array}{l} {a_{x{\rm{J}}2}} = - \frac{3}{2}\frac{{\mu {J_2}R_{\rm{E}}^2}}{{{r^5}}}x + \frac{{15}}{2}\frac{{\mu {J_2}R_{\rm{E}}^2{z^2}}}{{{r^7}}}x,\\ {a_{y{\rm{J}}2}} = - \frac{3}{2}\frac{{\mu {J_2}R_{\rm{E}}^2}}{{{r^5}}}y + \frac{{15}}{2}\frac{{\mu {J_2}R_{\rm{E}}^2{z^2}}}{{{r^7}}}y,\\ {a_{z{\rm{J}}2}} = - \frac{9}{2}\frac{{\mu {J_2}R_{\rm{E}}^2}}{{{r^5}}}z + \frac{{15}}{2}\frac{{\mu {J_2}R_{\rm{E}}^2{z^2}}}{{{r^7}}}z. \end{array} \right. $ |
式中:aJ2=[axJ2, ayJ2, azJ2]T;J2=0.001 082 63为地球扁率摄动常数;RE=6 378 137 m为地球平均半径;r为航天器的地心距.
为方便计算以及保证计算精度,需要对动力学方程中的变量进行归一化.在J2000坐标系中,长度量、时间量和质量分别以RE、
对于转移轨道设计问题,可将性能指标表示为
| $ \min J = \int_{{t_{\rm{0}}}}^{{t_{\rm{f}}}} {g\left( u \right){\rm{d}}t} . $ |
结合动力学模型(1),根据庞德里亚金极小值原理,引入拉格朗日乘子,构造哈密尔顿函数,有
| $ \begin{array}{l} H = \mathit{\boldsymbol{\lambda }}_r^{\rm{T}}\mathit{\boldsymbol{v + \lambda }}_v^{\rm{T}}\left( { - \frac{u}{{{r^3}}}\mathit{\boldsymbol{r}} - \frac{{{k_{{\rm{JR}}}}}}{{{r^5}}}{\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{r}} + \frac{{15{k_{{\rm{JR}}}}{z^2}}}{{2{r^7}}}\mathit{\boldsymbol{r}} + \frac{{{T_{\max }}u}}{m}\mathit{\boldsymbol{\alpha }}} \right) + \\ \;\;\;\;\;\;\;{\lambda _m}\left( { - \frac{{u{T_{\max }}}}{{{I_{{\rm{sp}}}}{g_0}}}} \right) + g\left( u \right). \end{array} $ |
式中:kJR=μJ2RE2,B1=[3/2, 0, 0;0, 3/2, 0;0, 0, 9/2]T,λ=[λr, λv, λm]T为拉格朗日乘子,也称为协态变量.
为使哈密尔顿函数取得极小值,对其求一阶偏导,可得欧拉方程为:
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot \lambda }}}_r} = - \frac{{\partial H}}{{\partial \mathit{\boldsymbol{r}}}} = \left( {\frac{u}{{{r^3}}} + \frac{{{k_{{\rm{JR}}}}}}{{{r^5}}}{\mathit{\boldsymbol{B}}_1} - \frac{{15{k_{{\rm{JR}}}}{z^2}}}{{2{r^7}}}} \right){\mathit{\boldsymbol{\lambda }}_v} - \\ \;\;\;\;\;\;\;\left( {\frac{{3\mu }}{{{r^5}}} + \frac{{5{k_{{\rm{JR}}}}}}{{{r^7}}}{\mathit{\boldsymbol{B}}_1} - \frac{{105{k_{{\rm{JR}}}}{z^2}}}{{2{r^9}}}} \right)\left( {\mathit{\boldsymbol{\lambda }}_v^{\rm{T}}\mathit{\boldsymbol{r}}} \right)\mathit{\boldsymbol{r}} - \frac{{15{k_{{\rm{JR}}}}}}{{{r^7}}}\left( {\mathit{\boldsymbol{\lambda }}_v^{\rm{T}}\mathit{\boldsymbol{r}}} \right){\mathit{\boldsymbol{B}}_2}\mathit{\boldsymbol{r}}, \end{array} $ | (2) |
| $ {{\mathit{\boldsymbol{\dot \lambda }}}_v} = - \frac{{\partial H}}{{\partial \mathit{\boldsymbol{v}}}} = - {\mathit{\boldsymbol{\lambda }}_r}, $ | (3) |
| $ {{\mathit{\boldsymbol{\dot \lambda }}}_m} = - \frac{{\partial H}}{{\partial m}} = - \frac{{u{T_{\max }}}}{{{m^2}}}\left\| {{\mathit{\boldsymbol{\lambda }}_\mathit{\boldsymbol{v}}}} \right\|. $ | (4) |
式中B2=[0, 0, 0;0, 0, 0;0, 0, 1]T.
根据最优控制理论,可推导得到最优推力方向为
| $ {\mathit{\boldsymbol{\alpha }}^ * } = - \frac{{{\mathit{\boldsymbol{\lambda }}_v}}}{{\left\| {{\mathit{\boldsymbol{\lambda }}_v}} \right\|}}. $ |
在对推力大小u的最优控制律进行推导时,需要考虑不同性能指标的影响:
1) 当性能指标为能量最优时,其最小化性能指标可以表示成
| $ {J_1} = \frac{{{T_{\max }}}}{{{I_{{\rm{sp}}}}{g_0}}}\int_{{t_0}}^{{t_{\rm{f}}}} {{u^2}{\rm{d}}t} , $ |
将其代入到哈密尔顿函数,并对哈密尔顿函数取极值,可得推力大小的最优控制律为
| $ \left\{ \begin{array}{l} {u^ * } = 1,{\rm{if}}\;S < - 1;\\ {u^ * } = 0,{\rm{if}}\;\mathit{S} > 1;\\ {u^ * } = \left( {1 - S} \right)/2,{\rm{if}}\;\left| S \right| \le 1. \end{array} \right. $ | (5) |
其中S为开关函数,其表达式为
| $ S = 1 - {\lambda _m} - \frac{{{I_{{\rm{sp}}}}{g_0}\left\| {{\mathit{\boldsymbol{\lambda }}_v}} \right\|}}{m}. $ |
2) 当性能指标为燃料最优时,其最小化性能指标可以表示成
| $ {J_2} = \frac{{{T_{\max }}}}{{{I_{{\rm{sp}}}}{g_0}}}\int_{{t_0}}^{{t_{\rm{f}}}} {u{\rm{d}}t} , $ |
同理可得其最优控制律为
| $ \left\{ \begin{array}{l} {u^ * } = 1,{\rm{if}}\;S < 0;\\ {u^ * } = 0,{\rm{if}}\;\mathit{S} > 0;\\ {u^ * } = \left[ {0,1} \right],{\rm{if}}\;S = 0. \end{array} \right. $ | (6) |
推导得到推力大小和推力方向的最优控制律后,可通过对动力学模型和欧拉方程进行积分,得到状态量和协态变量的瞬时值,再根据控制律得到推力大小和方向,从而将轨道优化问题转移成两点边值问题.
2 多次同伦方法在将转移轨道优化问题转换为两点边值问题之后,虽然理论上可通过打靶法对其进行求解,然而在实际求解过程中,存在下列3个难点:
1) 与只考虑地球中心引力的情况进行对比,由于J2项摄动的引入,动力学模型的非线性明显增强,增加了打靶收敛的难度;
2) 对于小推力转移轨道,其推力加速度一般为10-4m/s2量级,远小于地球引力,在轨道转移过程中需要作用很长时间才能改变轨道完成转移,从而在打靶过程中容易发散;
3) 从式(6)可以看出,对于燃料最优的转移轨道,其最优控制为Bang-Bang控制,推力u在开关函数S=0时刻存在突变,在对转移轨道进行积分过程中推力发生阶跃,不利于打靶求解.
针对上述3个问题,本文提出一种求解方法,通过多次同伦,依次解决存在的问题,从而得到最终的转移轨道.
2.1 动力学方程的同伦针对包含J2项摄动的动力学模型的复杂非线性问题,从简单动力学模型出发,先对不包含J2项,且采用“线性引力”假设的动力学模型进行求解,得到初始解,然后将动力学模型同伦到包含J2项摄动的真实引力的动力学模型.
“线性引力”近似是指将航天器受到的地球引力近似为大小不变、方向变化的力.引入第1个同伦参数ε1,在同伦过程中航天器的动力学模型为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot r}} = \mathit{\boldsymbol{v}},\\ \mathit{\boldsymbol{\dot v}} = \left( {1 - {\varepsilon _1}} \right)\left( { - \frac{\mu }{{\mathit{\boldsymbol{r}}_1^3}}\mathit{\boldsymbol{r}}} \right) + {\varepsilon _1}\left( { - \frac{\mu }{{\mathit{\boldsymbol{r}}_1^3}}\mathit{\boldsymbol{r}} + {\mathit{\boldsymbol{a}}_{{\rm{J}}2}}} \right) + \frac{{{T_{\max }}u}}{m}\mathit{\boldsymbol{\alpha }},\\ \dot m = - \frac{{{T_{\max }}u}}{{{I_{{\rm{sp}}}}{g_0}}}. \end{array} \right. $ | (7) |
式中:r1为近似的航天器地心距,在转移过程中为常值,不随航天器的位置变化而改变.式(7)中,第2式的右边第1项表示近似的线性引力,第2项表示地球中心引力和J2项摄动力,第3项为发动机推力.
针对同伦过程中的动力学模型,通过构造新的哈密尔顿函数,推导得到同伦过程中新的欧拉方程为:
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot \lambda }}}_r} = \left( {1 - {\varepsilon _1}} \right)\frac{\mu }{{r_1^3}}{\mathit{\boldsymbol{\lambda }}_v} + {\varepsilon _1}\left[ {\left( {\frac{u}{{{r^3}}} + \frac{{{k_{{\rm{JR}}}}}}{{{r^5}}}{\mathit{\boldsymbol{B}}_1} - \frac{{15{k_{{\rm{JR}}}}{z^2}}}{{2{r^7}}}} \right){\mathit{\boldsymbol{\lambda }}_v} - } \right.\\ \;\;\;\;\;\;\;\left. {\left( {\frac{{3\mu }}{{{r^5}}} + \frac{{5{k_{{\rm{JR}}}}}}{{{r^7}}}{\mathit{\boldsymbol{B}}_1} - \frac{{105{k_{{\rm{JR}}}}{z^2}}}{{2{r^9}}}} \right)\left( {\mathit{\boldsymbol{\lambda }}_v^{\rm{T}}\mathit{\boldsymbol{r}}} \right)\mathit{\boldsymbol{r}} - \frac{{15{k_{{\rm{JR}}}}}}{{{r^7}}}\left( {\mathit{\boldsymbol{\lambda }}_v^{\rm{T}}\mathit{\boldsymbol{r}}} \right){\mathit{\boldsymbol{B}}_2}\mathit{\boldsymbol{r}}} \right], \end{array} $ | (8) |
| $ {{\mathit{\boldsymbol{\dot \lambda }}}_v} = - \frac{{\partial H}}{{\partial \mathit{\boldsymbol{v}}}} = - {\mathit{\boldsymbol{\lambda }}_r}, $ | (9) |
| $ {{\dot \lambda }_m} = - \frac{{\partial H}}{{\partial m}} = - \frac{{u{T_{\max }}}}{{{m^2}}}\left\| {{\mathit{\boldsymbol{\lambda }}_v}} \right\|. $ | (10) |
相比较于原来的欧拉方程式(2)~(4),推导得到同伦过程中的欧拉方程式(8)~(10)中,只有位置协态变量λr的积分方程式(8)发生变化,而关于速度协态变量λv的式(9)和质量协态变量λm的式(10)保持不变.
对于动力学模型式(7),在同伦初始时刻,即ε1=0时,航天器只受到线性引力,在对其进行优化时不需要考虑J2摄动,则此时式(8)可简化为
| $ {{\mathit{\boldsymbol{\dot \lambda }}}_r} = - \frac{{\partial H}}{{\partial \mathit{\boldsymbol{r}}}} = \frac{\mu }{{r_l^3}}{\mathit{\boldsymbol{\lambda }}_v}. $ |
与包含J2项摄动时的欧拉方程相比,虽然只有λr的积分方程的非线性明显降低,但由于λr和λv相互耦合,导致λv的非线性也相应降低,而最优推力方向只与λv相关,推力又影响航天器状态量的变化,因此,采用线性引力假设,大幅降低了整个动力学系统的非线性,从而改善了初始问题的求解难度.
2.2 推力幅值的同伦对于推力值过小导致的打靶不收敛问题,先在大推力幅值的情况下进行打靶求解,然后通过对推力值的大小进行同伦,得到小推力下的转移轨道.
对动力学模型中的推力幅值,引入第2个同伦参数ε2,则在同伦过程中,推力幅值为
| $ {T_{\max }} = \left( {1 - {\varepsilon _2}} \right){T_1} + {\varepsilon _2}{T_2}. $ |
式中:T1为初始时的较大推力,T2为所需计算的小推力幅值.
在对推力大小进行同伦时,推力从大到小变化.若航天器的转移时间自由,则随着推力减小,航天器改变轨道状态的能力减弱,完成相同的轨道转移需要消耗更多的时间,转移轨道圈数也随之增加.文献[9]中对于时间最优的小推力转移轨道进行研究,在同伦过程中发现在圈数增加的某些时刻,同伦轨迹会发生突变,一般的同伦方法不能顺利进行,因此提出二次同伦方法,克服了该同伦过程中存在的问题.
虽然二次同伦方法可以解决转移圈数发生变化时产生的问题,但是所需计算时间较长,因此,在本文中,对转移时间给定,在同伦过程中不改变转移时间和转移圈数,则不需要进行二次同伦方法即可完成该同伦过程.
在确定转移时间时,先根据Lambert算法确定转移所需的速度增量ΔV,再按照下式计算所需消耗的燃料为
| $ \Delta m = {m_0}\left( {1 - \exp \left( { - \Delta V/\left( {{I_{{\rm{sp}}}}{g_0}} \right)} \right)} \right). $ | (11) |
根据动力学模型式(1),可以计算得到航天器推力始终保持最大时的质量消耗率
| $ {t_{\rm{f}}} = 1.5\Delta m/{{\dot m}_{\max }}. $ | (12) |
按照此原则选取得到的转移时间,航天器该时间内能完成轨道转移,同时不会消耗过多时间.
2.3 性能指标的同伦针对燃料最优的Bang-Bang控制问题,根据Bertrand等[14]在2002年提出的同伦方法,通过构造从能量最优到燃料最优平滑过渡的性能指标,从而降低求解难度.
通过引入第3个同伦参数ε3,构造新的性能指标为
| $ J = \frac{{{T_{\max }}}}{{{I_{{\rm{sp}}}}{g_0}}}\int_{{t_0}}^{{t_{\rm{f}}}} {\left( {1 - {\varepsilon _3}} \right){u^2} + {\varepsilon _3}u{\rm{d}}t} . $ |
当ε3:0→1过程中,性能指标从能量最优转变为燃料最优.根据最优性一阶必要条件,推力大小u的控制律为
| $ \left\{ \begin{array}{l} {u^ * } = 1,{\rm{if}}\;S < - q;\\ {u^ * } = 0,{\rm{if}}\;\mathit{S} > q;\\ {u^ * } = 0.5\left( {1 - S/q} \right),{\rm{if}}\;\left| S \right| \le q. \end{array} \right. $ |
式中:q=1-ε3,当ε3≠1时,u为连续控制力,且ε3趋近于1时,即可得到燃料最优的转移轨道.
得到性能指标为能量最优的转移轨道之后,对同伦参数ε3按照一定步长进行迭代计算,最终可得到燃料最优的转移轨道.
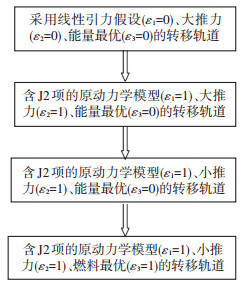
在实际求解过程中的同伦初始问题,单独采用上述3种同伦的任意一种进行打靶求解,都存在很大难度.同时设置3个同伦参数均为0,即采用“线性引力”假设,不考虑J2项摄动,发动机推力幅值较大,性能指标为能量最优的情况下,打靶法才能快速收敛,然后再对这3个参数进行同伦.多次同伦方法的同伦过程如图 1所示,分别对同伦参数ε1、ε2和ε3依次同伦,最终得到原问题的小推力燃料最优转移轨道.
|
图 1 多次同伦过程流程 Figure 1 The flow chart of multiple homotopy |
以第八届全国空间轨道设计竞赛的甲题为例,航天器对位于太阳同步轨道的空间碎片进行交会,其动力学模型需考虑地球扁率J2项的摄动影响.航天器初始质量为1 000 kg,发动机最大推力Tmax=0.5 N,发动机比冲Isp=1 000 s.以半长轴为7 250 km,偏心率为0,轨道倾角为98.5°的轨道为例,航天器在该轨道上受到的地球中心引力加速度为aE=7.583 4 m/s2,由J2项摄动引起的最大引力加速度为aJ2=1.855 2×10-2 m/s2,发动机推力产生的加速度为aT=5×10-4 m/s2.对比可知,航天器的发动机推力远小于受到的地球引力,甚至比J2项摄动力还要小两个量级,若直接求解该动力学模型下的小推力最优转移轨道,打靶法难以收敛,因此采用本文提出的多次同伦方法对其进行求解.
本文对航天器从前一个碎片出发,到后一个碎片交会的转移轨道进行优化设计.对于本算例中的交会问题,交会精度在计算过程中体现为打靶精度,在对状态量进行归一化后,本文中的打靶精度设为1×10-8,即交会精度小于0.063 8m和7.905 4× 10-5 m/s.本算例中的计算在CPU为i5-4590,主频为3.30 GHz,内存为8 G的台式计算机上进行,计算平台为MATLAB2015a,积分程序转换为mexw32文件后利用fsolve函数进行打靶求解.
经过初步选取,得到两个碎片的轨道要素见表 1,其中历元时刻是指对应于该轨道要素的约化儒略日.以碎片2的当前时刻为交会时刻,先将碎片1积分到交会时刻,得到碎片1在交会时刻的轨道;计算碎片1与碎片2的Lambert转移所需速度增量ΔV,根据式(11)计算得到Δm=5.794 35 kg,再根据式(12)确定转移时间为tf=1.973 0 d;然后对碎片1积分,得到航天器出发时刻的所在位置,从而确定转移轨道初始时刻的状态量、终端时刻的状态量和转移时间.转移轨道初始状态量和终端状态量见表 2.
| 表 1 初步选取的两个碎片的轨道要素 Table 1 The elements of selected satellite debris |
| 表 2 归一化后的转移轨道的初始状态和终端状态 Table 2 The non-dimensionalized initial state and final state of the satellite |
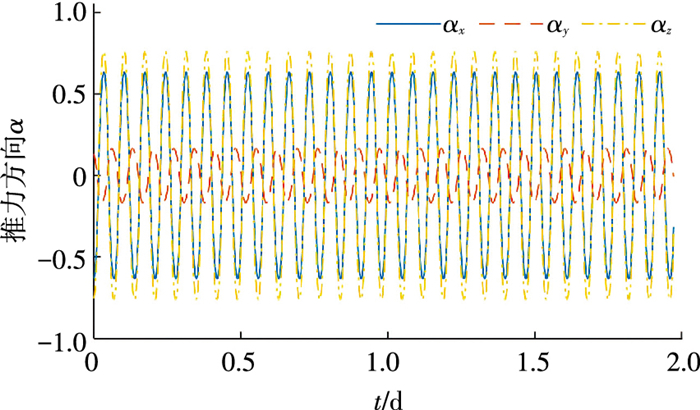
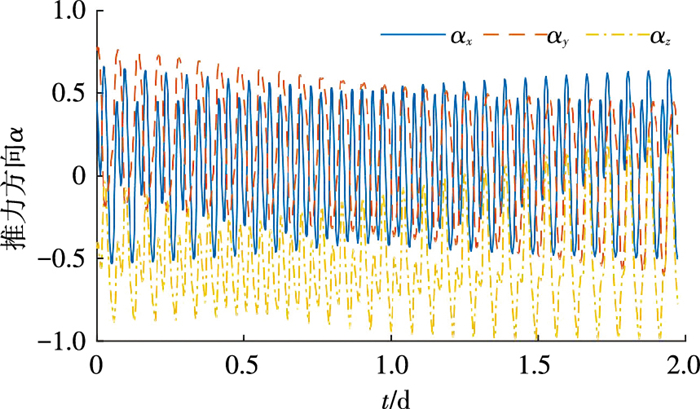
对于推力幅值的同伦,设初始时的最大推力为T1=30 N.当ε1=ε2=ε3=0时,利用MATLAB的fsolve函数进行打靶,很容易得到收敛解.先对动力学方程进行同伦,ε1从0增加到1,得到原动力学模型下的大推力能量最优转移轨道.在此同伦过程中,同伦初始时(即ε1=ε2=ε3=0)的最优推力方向随时间的变化曲线如图 2所示,同伦结束时(即ε1=1,ε2=ε3=0)的最优推力方向如图 3所示.从图中可以看出,图 2中的推力方向近似于周期变化,图 3中的推力方向变化更为剧烈,这是同伦过程中动力学模型的非线性增强所导致的,同时这也可以解释采用“线性引力”假设更容易得到收敛解的原因.
|
图 2 ε1=ε2=ε3=0时的推力方向随时间的变化曲线 Figure 2 Time histories of thrust direction when ε1=ε2=ε3=0 |
|
图 3 ε1=1, ε2=ε3=0时的推力方向随时间的变化曲线 Figure 3 Time histories of thrust direction when ε1=1, ε2=ε3=0 |
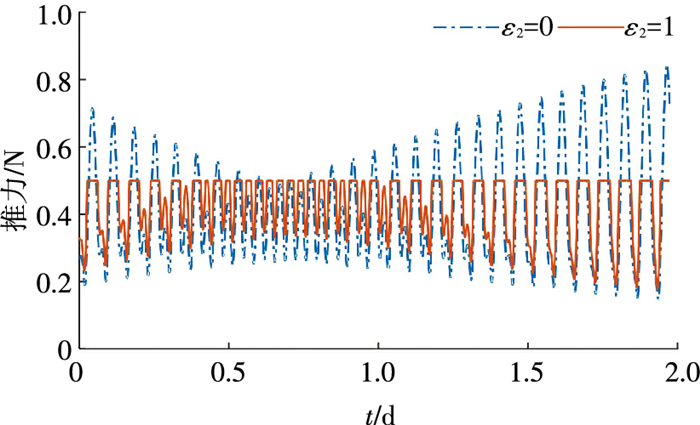
然后对推力最大幅值进行同伦.在此同伦过程中,始终保持ε1=1, ε3=0,ε2从0增加到1.对该同伦初始时刻和结束时刻的转移轨道的推力大小随时间的变化曲线进行对比,如图 4所示.当ε2=0时,Tmax=T1=30 N,由式(5)可知,在转移过程中发动机推力在0和Tmax之间变化,而优化得到的推力幅值始终不大于1 N;当ε2=1时,Tmax=T2=0.5 N,在转移过程中,推力多次达到最大值.
|
图 4 推力同伦过程中推力大小随时间变化曲线 Figure 4 Time histories of the optimal thrust magnitude |
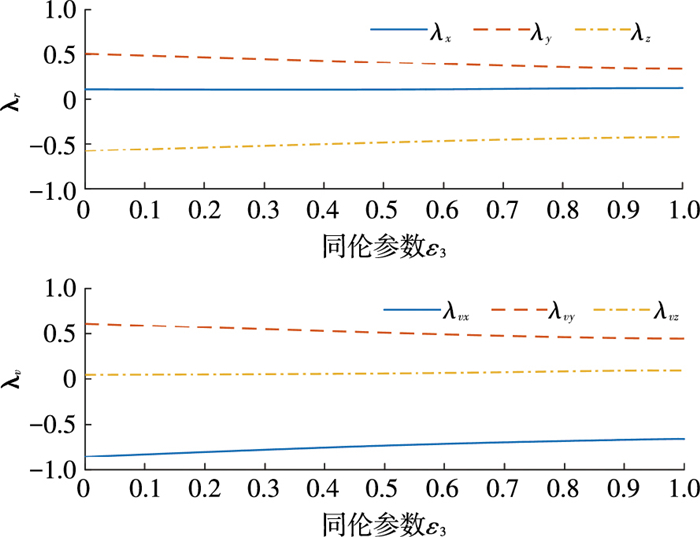
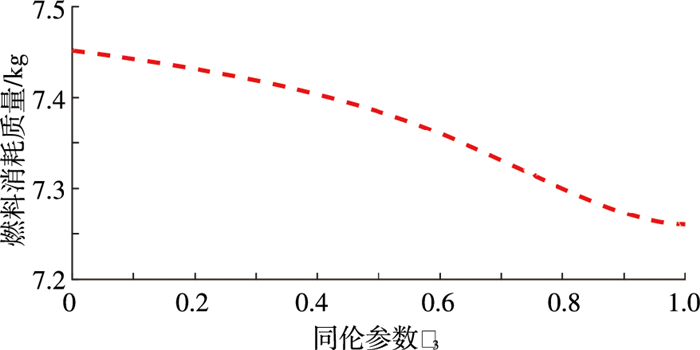
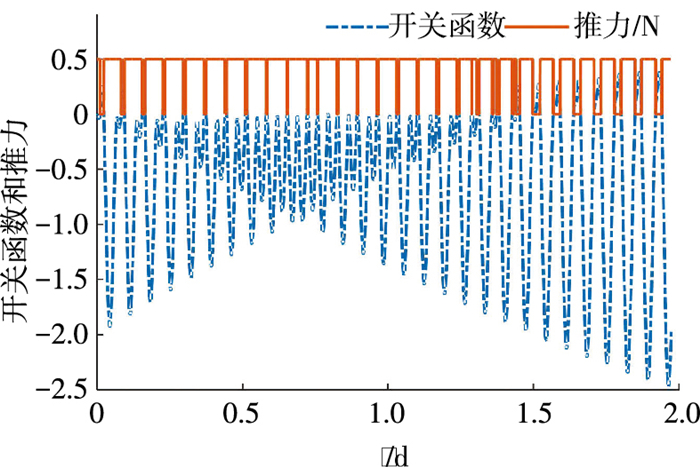
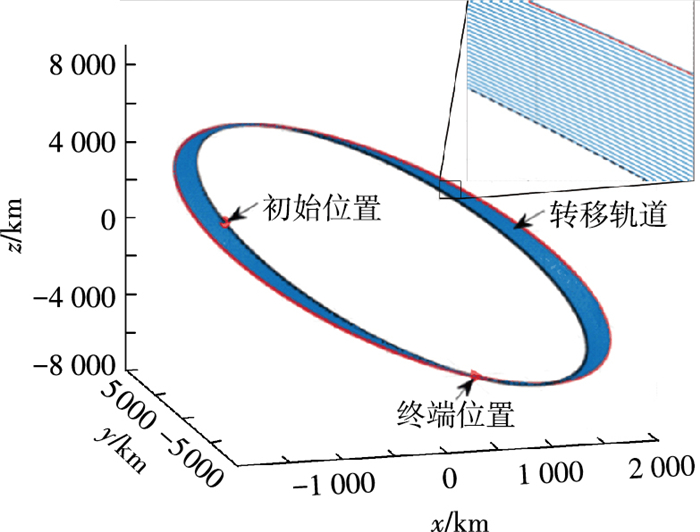
最后对性能指标进行同伦,令ε3:0→1,从而使性能指标从能力最优转变为燃料最优.此同伦过程中的位置协态变量初值λr0和速度协态变量初值λv0随同伦参数的变化曲线如图 5所示.从图 5中可以看出,协态变量的变化比较缓慢均匀,不存在突变跳跃的情况,同伦过程比较顺利.同伦过程中航天器的燃料消耗质量变化曲线如图 6所示,从能量最优时需要消耗7.454 3 kg减小到燃料最优时的7.260 2 kg.当ε3=1时,得到燃料最优转移轨道,此时的推力为Bang-Bang控制,开关函数和推力变化曲线如图 7所示,发动机在转移过程中开机次数达到33次.燃料最优的小推力转移轨道如图 8所示,航天器需要运行约28圈才能完成轨道转移,从而对碎片2进行交会.
|
图 5 性能指标同伦过程中协态变量随同伦参数的变化曲线 Figure 5 The homotopic path of initial costates in the homotopy of index performance |
|
图 6 性能指标同伦过程中航天器燃料消耗质量变化 Figure 6 The fuel consumption in the homotopy of index performance |
|
图 7 燃料最优时的开关函数和推力大小随时间变化曲线 Figure 7 The switching function and optimal thrust profiles of fuel optimal transfer trajectory |
|
图 8 燃料最优的转移轨道 Figure 8 The fuel-optimal low thrust transfer trajectory |
本算例计算过程中,共用时1 055 s,其中在打靶过程中对动力学模型的积分时间为1 023 s,在3次同伦过程中,同伦次数分别为246次、99次、72次.与文献[15]进行对比,其利用间接法进行优化,利用粒子群法得到打靶初值,再通过同伦得到所需解,利用C++语言编译.其中水星交会的算例的转移圈数为4圈,对于燃料最优的性能指标,粒子群法无法得到合适的初始值;对于能量最优,粒子群法得到初始值所需时间为338 s,然后再通过同伦得到燃料最优解,而本文中初始问题的打靶时间少于3 s;对于文献[15]中的近地轨道长时间交会算例,转移时间为15 d,计算用时为5.45~11.02 h,该算例与本文的不同之处在于其交会时间较长,在交会过程中未考虑J2项摄动,而本文中的动力学模型的复杂程度要远高于该算例.综合上述对比分析,本文所提出的多次同伦方法具有更好的普适性及更快的求解速度.
4 结论1) 对动力学模型及性能指标同伦的相关公式进行推导,得到同伦过程中的最优性条件及最优控制律.
2) 同伦初始问题为采用“线性引力”假设的较大推力转移轨道优化问题,由于其非线性较弱,容易收敛,利用打靶法易于得到解,且得到的最优推力方向近似于周期变化.
3) 通过引入3个同伦参数,分别对动力学模型、推力大小和性能指标进行同伦,可以克服由于推力小、J2摄动引起的模型非线性强等原因所导致的求解困难,最终得到所需的燃料最优转移轨道.
| [1] |
张俊. 基于开普勒二体运动修正地球扁率J2摄动项算法[J].
航天控制, 2014, 32(6): 22-25.
ZHANG Jun. The correction algorithm of J2 perturbation of the Earth oblateness based on Kepler two-body motion[J]. Aerospace Control, 2014, 32(6): 22-25. DOI: 10.3969/j.issn.1006-3242.2014.06.005 |
| [2] |
张锦绣, 曹喜滨, 张刘, 等. J2项摄动下的Lambert问题算法研究[J].
哈尔滨工业大学学报, 2009, 41(5): 6-9.
ZHANG Jinxiu, CAO Xibin, ZHANG Liu, et al. An algorithm for lambert's solution based on J2 perturbation[J]. Journal of Harbin institute of technology, 2009, 41(5): 6-9. |
| [3] |
王斌. 基于Lambert问题的J2摄动空间交会策略[D]. 哈尔滨: 哈尔滨工业大学, 2016.
WANG Bin. J2 perturbation space rendezvous strategy based onlambert problem[D]. Harbin: Harbin Institute of Technology, 2016. |
| [4] |
张洪波, 郑伟, 汤国建. 采用打靶法设计考虑地球扁率的机动轨道[J].
宇航学报, 2008, 29(4): 1177-1181.
ZHANG Hongbo, ZHENG Wei, TANG Guojian. Maneuver trajectory design with J2 correction based on shooting procedure[J]. Journal of Astronautics, 2008, 29(4): 1177-1181. DOI: 10.3873/j.issn.1000-1328.2008.04.017 |
| [5] |
周军, 常燕. 考虑地球扁率J2摄动影响的异面椭圆轨道多冲量最优交会[J].
宇航学报, 2008, 29(2): 472-475.
ZHOU Jun, CHANG Yan. Optimal multiple-impulse rendezvous between non-coplanar elliptic orbits considering the J2 perturbation effects[J]. Journal of Astronautics, 2008, 29(2): 472-475. DOI: 10.3873/j.issn.1000-1328.2008.02.015 |
| [6] |
ROSCOE C W T, WESTPHAL J J, GRIESBACH J D, et al. Formation establishment and reconfiguration using differential elements in J2-perturbed orbits[J].
Journal of Guidance, Control, and Dynamics, 2015, 38(9): 1725-1740.
DOI: 10.2514/1.G000999 |
| [7] |
李俊峰, 蒋方华. 连续小推力航天器的深空探测轨道优化方法综述[J].
力学与实践, 2011, 33(3): 1-6.
LI Junfeng, JIANG Fanghua. Survey of low-thrust trajectory optimization methods for deep space exploration[J]. Mechanics in Engineering, 2011, 33(3): 1-6. |
| [8] |
JIANG Fanghua, BAOYIN Hexi, LI Junfeng. Practical techniques for low-thrust trajectory optimization with homotopic approach[J].
Journal of Guidance, Control, and Dynamics, 2012, 35(1): 245-258.
DOI: 10.2514/1.52476 |
| [9] |
PAN Binfeng, LU Ping, PAN Xun, et al. Double-homotopy method for solving optimal control problems[J].
Journal of Guidance, Control, and Dynamics, 2016, 39(8): 1706-1720.
DOI: 10.2514/1.G001553 |
| [10] |
WU Baolin, WANG Danwei, POH E K, et al. Nonlinear optimization of low-thrust trajectory for satellite formation: Legendre pseudospectral approach[J].
Journal of Guidance, Control, and Dynamics, 2009, 32(4): 1371-1381.
DOI: 10.2514/1.37675 |
| [11] |
SCHEEL W A, CONWAY B A. Optimization of very-low-thrust, many-revolution spacecraft trajectories[J].
Journal of Guidance, Control, and Dynamics, 1994, 17(6): 1185-1192.
DOI: 10.2514/3.21331 |
| [12] |
李亮, 和兴锁, 张娟, 等. 考虑地球扁率影响的任意椭圆轨道小推力最优交会控制[J].
西北工业大学学报, 2005, 23(3): 401-405.
LI Liang, HE Xingsuo, ZHANG Juan, et al. Optimal low thrust power rendezvous between neighboring elliptic orbits considering the oblateness of Earth[J]. Journal of Northwestern Polytechnical University, 2005, 23(3): 401-405. DOI: 10.3969/j.issn.1000-2758.2005.03.028 |
| [13] |
韩威华, 甘庆波, 王晓光, 等. 摄动情况下有限推力轨道转移与交会联合优化[J].
系统工程与电子技术, 2013, 35(7): 1486-1491.
HAN Weihua, GAN Qingbo, WANG Xiaoguang, et al. Comprehensive optimization for orbit transfer and rendezvous of finite thrust with perturbation[J]. Systems Engineering and Electronics, 2013, 35(7): 1486-1491. DOI: 10.3969/j.issn.1001-506X.2013.07.22 |
| [14] |
BERTRAND R, EPENOY R. New smoothing techniques for solving bang-bang optimal control problems numerical results and statistical interpretation[J].
Optimal Control Applications and Methods, 2002, 23(4): 171-197.
DOI: 10.1002/oca.709 |
| [15] |
李俊峰, 宝音贺西, 蒋方华, 等.
深空探测动力学与控制[M]. 北京: 清华大学出版社, 2014.
LI Junfeng, BAOYIN Hexi, JIANG Fanghua, et al. Dynam ics and control of interplanetary flight[M]. Beijing: Tsinghua University Press, 2014. |
 2017, Vol. 49
2017, Vol. 49


