近十几年航天任务蓬勃发展,各类轨道上运行着上千颗人造卫星.在过去十年内的各类航天任务里,约有10%的航天器未能正常入轨或在轨失效.地球同步轨道的轨道资源有限,即能够容纳的同步轨道卫星数量有限,因此轨道价值极高.由于在轨器件失效、燃料消耗殆尽或者卫星寿命到期,一部分地球同步轨道卫星已经不能提供相应的服务,但仍然占据着宝贵的轨道位置.因此,对此类失效(非合作)卫星进行在轨服务,例如燃料加注、部件升级或者抓捕离轨等具有重要的意义[1],多个国家已开展或正在计划开展航天器空间在轨服务任务[2].
服务航天器逼近目标航天器的整个阶段通常可分为自由滑行段、霍曼转移阶段、径向脉冲逼近阶段、直线逼近阶段[3].针对前3个阶段的相对导航问题已经有了深入研究,并取得了大量成果[4].本文针对在轨服务最后直线逼近段的视觉相对状态测量问题进行研究,现有的视觉导航方法主要针对合作航天器,即在目标航天器上安装有专用于视觉导航的特征靶标[3, 5].对于没有安装用于视觉测量特征靶标的目标航天器,只能采用目标航天器的自然结构特征作为测量目标.曹彩秀[6]以整个太阳能帆板三角形支架为测量目标,基于滑动窗口Hough变化提出了自主识别算法,将其转换为共面四点透视(P4P)问题,但该算法受测量误差的影响较大.苗锡奎等[7]提出了以整个太阳能帆板为测量目标的视觉导航方法,但并没有考虑相机视场的限制.张鑫等[8]提出了基于SoftPOSIT的相对位姿估计方法,其在特征点匹配过程中解算位姿,但在近距离阶段难以保证提取到算法所需的特征点数目.
综上所述,本文考虑非合作航天器最终接近段视觉测量方案受视觉相机视场和焦距的限制,提出了一种新的测量方案和相对位姿估计算法.
1 测量方案如图 1所示,视觉相机与服务航天器以“自拍杆”的安装结构连接,服务航天器的一部分结构在视觉相机的视场范围内.该安装结构可以有效增加相机到目标航天器的距离,即使在服务航天器完成目标航天器抓捕动作时,仍能保证相机距目标有2 m左右的观测距离.此外,由于在发射过程中服务航天器结构的变化以及相机结构的展开误差,需要对视觉测量相机的外部和内部参数进行在轨标定,该部分是视觉导航的前提.在服务航天器的表面贴有同心圆环,如图 1中服务航天器表面的红色同心圆环,并保证同心圆环在视觉相机的视场范围内.由于同心圆环的尺寸和相对位置已知,并且具有较高的精度,可以用来完成视觉相机的标定工作[9],获取视觉相机的外部和内部参数,从而提高接近阶段视觉测量精度.本文的重点不在视觉相机标定,故不进行进一步的介绍.
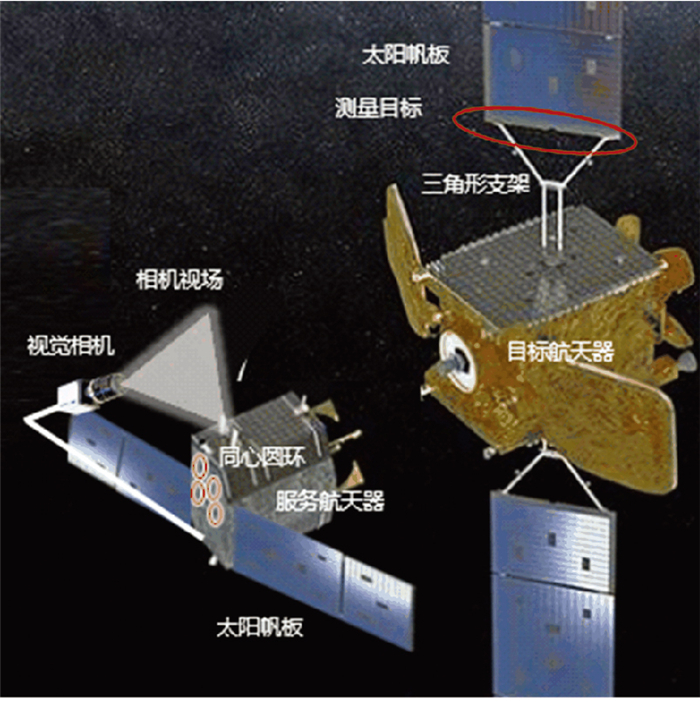
|
图 1 视觉测量方案 Figure 1 Vision measurement scheme |
在非合作航天器交会对接的最终接近段,由于距离较短,受视觉相机视场的约束,无法测量到整个目标航天器或者整个太阳帆板.针对这一特殊问题,本文以太阳帆板三角形支架的部分结构为测量目标;利用“自拍杆”安装结构增加视觉相机与目标航天器之间的相对距离,从而达到增大视场的作用并实现相机的有效对焦;调整视觉相机到合适的安装角度使得测量目标和同心圆环同时处于视场范围内.视觉相机的安装角为相机坐标系与服务航天器体坐标系之间的欧拉角,它决定着这两个坐标系之间的相对旋转矩阵Rsc,并定义其相对位移矢量为Tsc.
定义某一测量目标在服务航天器体坐标系中的坐标为Ps, n=[xs, n, ys, n, zs, n]T,那么其在相机坐标系中的坐标为Pc, n=[xc, n, yc, n, zc, n]T= RscPs, n+Tsc.定义相机视场为s,工作距离为l,满足
| $ s = \frac{{\lambda \left( {l - f} \right)}}{f}, $ | (1) |
式中:f、λ分别为焦距和敏感元件尺寸比例因子.若某一测量目标在视觉相机的视场内,则满足
| $ \frac{{\lambda \left( {{z_{{\rm{c}},n}} - f} \right)}}{f} \ge \sqrt {x_{{\rm{c}},n}^2 + y_{{\rm{c}},n}^2} . $ |
相机安装角的确定与航天器构型、尺寸大小、抓捕位置、相机视场角、“自拍杆”长度等因素有关,由于不是本文的研究重点故没有进行详细的分析和计算.通常视觉相机安装角度的选取准则如下:
1) 相机视场需要覆盖同心圆环标定靶标和测量目标两个部分,在保证同心圆环被完全观测的前提下使更多的视场用来观测目标.
2) 由式(1)可知,相机视场随着工作距离增大而增大,考虑最终接近段航天器间相对运动变化范围不大,通常保证服务航天器完成抓捕时测量目标能被观测即可.
2 问题描述 2.1 坐标系定义定义3个坐标系:目标体坐标系、图像平面坐标系和相机坐标系.目标体坐标系Ot-XtYtZt:其与目标航天器固连,原点位于目标航天器质心,3个坐标轴分别与目标航天器的惯量主轴平行,特征在其坐标中的定义为Pt, n=[xt, n, yt, n, zt, n]T;图像平面坐标系Oi-XiYi:其原点位于相机主轴与成像平面的交点,Xi轴平行于图像的横向,Xi轴平行于图像的纵向,特征在其坐标中的定义为Pi, n=[xi, n, yi, n]T;相机坐标系Oc-XcYcZc:其原点在相机中心,Zc轴垂直于成像平面,Xc、Yc轴分别平行于Xi和Yi轴,特征在其坐标中的定义为Pc, n=[xc, n, yc, n, zc, n]T.
2.2 成像模型如图 2所示,测量目标是太阳帆板三角形支架的部分结构,其为线特征,而一条线段可以用两个点来描述:线段的长度为两点之间的距离,线段方向为一个点指向另一个点.基于针孔成像模型,利用线段间的交点或线段端点来建立模型:
| $ {\mathit{\boldsymbol{P}}_{{\rm{c}},n}} = \mathit{\boldsymbol{R}}{\mathit{\boldsymbol{P}}_{{\rm{t}},n}} + \mathit{\boldsymbol{T}}, $ | (2) |
| $ {x_{{\rm{i}},n}} = f\frac{{{x_{{\rm{c}},n}}}}{{{z_{{\rm{c}},n}}}} + {\delta _x}, $ | (3) |
| $ {y_{{\rm{i}},n}} = f\frac{{{y_{{\rm{c}},n}}}}{{{z_{{\rm{c}},n}}}} + {\delta _y}. $ | (4) |
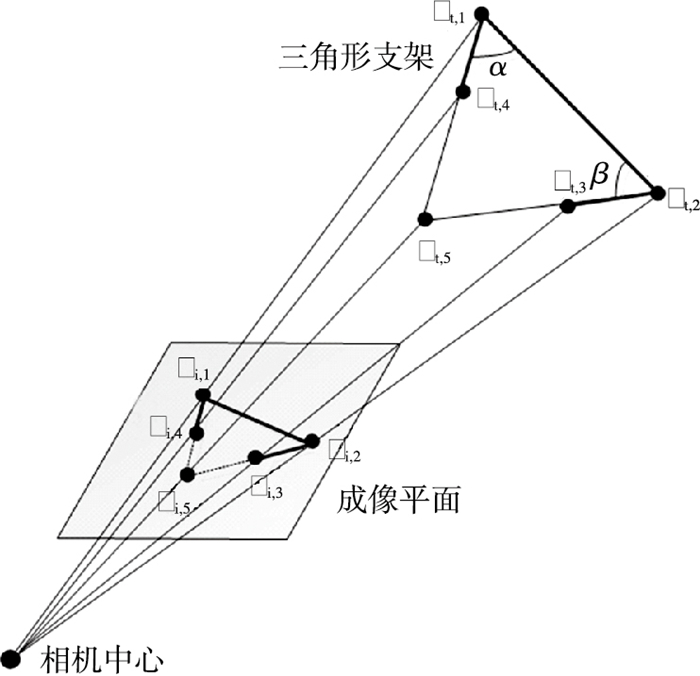
|
图 2 坐标系关系和成像模型 Figure 2 Coordinate relation and imaging model |
式中:R、T分别为目标体坐标系相对相机坐标系的旋转矩阵和位移矢量;δx、δy分别为横向测量误差和纵向测量误差.注意:在实际应用中,一般已知相机坐标系与服务航天器体坐标系之间的转换关系,便可以得到目标航天器与服务航天器之间的相对位姿.为了简化推导过程,后面都以R和T作为两个航天器之间的相对位姿.
3 相对位姿估计算法 3.1 逆投影原理当没有测量误差时,特征点Pc, n应该位于从相机中心Oc指向图像平面对应投影点Pi, n的射线上,由于射线OcPi, n的方向与特征点Pc, n向图像平面投影的方向相反,因此射线OcPi, n称为逆投影线,该原理为逆投影原理[10].射线OcPi, n的方向矢量为
| $ {\mathit{\boldsymbol{v}}_n} = {\left[ {\frac{{{x_{{\rm{i}},n}}}}{f},\frac{{{y_{{\rm{i}},n}}}}{f},1} \right]^{\rm{T}}}. $ | (5) |
定义景深dn,则可得Pc, n=dn·vn和dn=zc, n,有如下关系:
| $ {k_{xz,n}} = \frac{{{x_{{\rm{i}},n}} + {\delta _x}}}{f} = \frac{{{x_{{\rm{c}},n}}}}{{{z_{{\rm{c}},n}}}}, $ | (6) |
| $ {k_{yz,n}} = \frac{{{y_{{\rm{i}},n}} + {\delta _y}}}{f} = \frac{{{y_{{\rm{c}},n}}}}{{{z_{{\rm{c}},n}}}}. $ | (7) |
由式(5)~式(7)可得
| $ {\mathit{\boldsymbol{P}}_{{\rm{c}},n}} = {\left[ {{k_{xz,n}}{d_n},{k_{yz,n}}{d_n},{d_n}} \right]^{\rm{T}}}. $ | (8) |
由式(8)可知,当提取到特征点在图像平面坐标系中对应的投影坐标时,特征点Pc, n可用景深dn表示.
3.2 最优空间几何构型太阳帆板三角形支架测量模型如图 2所示,相机测量到的目标为三角形支架部分结构(图中粗线部分).已知太阳帆板三角形支架实际空间几何构型约束为:
1) 线段长度|Pt, 1Pt, 2|=l;
2) 线段Pt, 1Pt, 2和线段Pt, 1Pt, 4的夹角为α,线段Pt, 1Pt, 2和线段Pt, 2Pt, 3的夹角为β.
已知的坐标位置为:
1) 线段端点和交点投影坐标为Pi, n=[xi, n, yi, n]T, (n=1, 2, 3, 4);
2) 支架顶点坐标为Pt, n=[xt, n, yt, n, zt, n]T, (n=1, 2, 5).
根据成像原理,由投影点Pi, 5是投影线段Pi, 1Pi, 4和投影线段Pi, 2Pi, 3的交点来求得Pt, 5的投影坐标,由式(8)可得3个顶点在相机坐标系中的坐标,并得到满足太阳帆板三角形支架实际空间几何构型约束的非线性方程组:
| $ \left\{ \begin{array}{l} \left| {{\mathit{\boldsymbol{P}}_{{\rm{c}},1}}{\mathit{\boldsymbol{P}}_{{\rm{c}},2}}} \right| = \sqrt {{{\left( {{k_{xz,1}}{d_1} - {k_{xz,2}}{d_2}} \right)}^2} + {{\left( {{k_{yz,1}}{d_1} - {k_{yz,2}}{d_2}} \right)}^2} + {{\left( {{d_1} - {d_2}} \right)}^2}} = l,\\ \frac{{\left| {{\mathit{\boldsymbol{P}}_{{\rm{c}},1}}{\mathit{\boldsymbol{P}}_{{\rm{c}},2}}} \right|}}{{2\left| {{\mathit{\boldsymbol{P}}_{{\rm{c}},1}}{\mathit{\boldsymbol{P}}_{{\rm{c}},5}}} \right|}} = \frac{{\sqrt {{{\left( {{k_{xz,1}}{d_1} - {k_{xz,2}}{d_2}} \right)}^2} + {{\left( {{k_{yz,1}}{d_1} - {k_{yz,2}}{d_2}} \right)}^2} + {{\left( {{d_1} - {d_2}} \right)}^2}} }}{{2\sqrt {{{\left( {{k_{xz,1}}{d_1} - {k_{xz,5}}{d_5}} \right)}^2} + {{\left( {{k_{yz,1}}{d_1} - {k_{yz,5}}{d_5}} \right)}^2} + {{\left( {{d_1} - {d_5}} \right)}^2}} }} = \cos \alpha ,\\ \frac{{\left| {{\mathit{\boldsymbol{P}}_{{\rm{c}},1}}{\mathit{\boldsymbol{P}}_{{\rm{c}},2}}} \right|}}{{2\left| {{\mathit{\boldsymbol{P}}_{{\rm{c}},2}}{\mathit{\boldsymbol{P}}_{{\rm{c}},5}}} \right|}} = \frac{{\sqrt {{{\left( {{k_{xz,1}}{d_1} - {k_{xz,2}}{d_2}} \right)}^2} + {{\left( {{k_{yz,1}}{d_1} - {k_{yz,2}}{d_2}} \right)}^2} + {{\left( {{d_1} - {d_2}} \right)}^2}} }}{{2\sqrt {{{\left( {{k_{xz,2}}{d_2} - {k_{xz,5}}{d_5}} \right)}^2} + {{\left( {{k_{yz,2}}{d_2} - {k_{yz,5}}{d_5}} \right)}^2} + {{\left( {{d_2} - {d_5}} \right)}^2}} }} = \cos \beta . \end{array} \right. $ | (9) |
通过求解式(9)便得到景深dn.注意:太阳帆板三角形支架通常为等腰三角形,即满足α=β,才有式(9)中等式2和等式3的成立.换成普通三角形,只是形式上有所变化,并不影响本文算法的可行性.由于存在测量误差,特征点Pc, n通常不在逆投影线OcPi, n上,因此问题实质为在基于逆投影原理上求解最满足三角形支架实际构型约束的空间几何构型,称为最优空间几何构型,并得到相应的景深dn.
3.3 基于蚁群搜索算法的非线性优化求解景深dn即为求解式(9)的非线性方程组,该方程组由3个方程组成,涉及3个变量,可以采用多种方法求解.牛顿迭代法[11]是求解非线性方程组最常用的算法之一,它具有算法简单、精度高等优点,但是十分依赖迭代初值的选取.Levenberg-Marquardt算法[12]是使用最广泛的非线性最小二乘算法,其对过参数化问题不敏感、求解速度快,但极其依赖方程组解处的雅可比矩阵非奇异.近十几年进化算法在各领域得到了广泛应用,如蚁群搜索算法[13-14],它具有以下优点:鲁棒性强、正反馈机制、全局搜索能力强、算法实现简单等.考虑到图像测量误差,初始景深和运动特性未知等因素,蚁群搜索算法更适合应用到求解本文所涉及的非线性方程组.
采用蚁群搜索算法求解非线性方程组需要将非线性方程组转换为非线性优化问题,然后将蚁群所有可走的路径构成待优化函数的解空间,而蚁群实际所走的路径就是可行解.在蚁群搜索算法的迭代过程中,蚂蚁行径路径越短,该蚂蚁所释放的信息素就越多,则随着迭代的深入,在较短路径上遗留的信息素浓度就会逐渐增大,从而趋向该路径的蚂蚁数量也会逐渐增多.最终,由于正反馈作用,整个蚁群汇合到最佳路径上,从而找到非线性方程组的最优解.基于蚁群搜索算法求解景深dn的流程如图 3所示,具体过程如下.
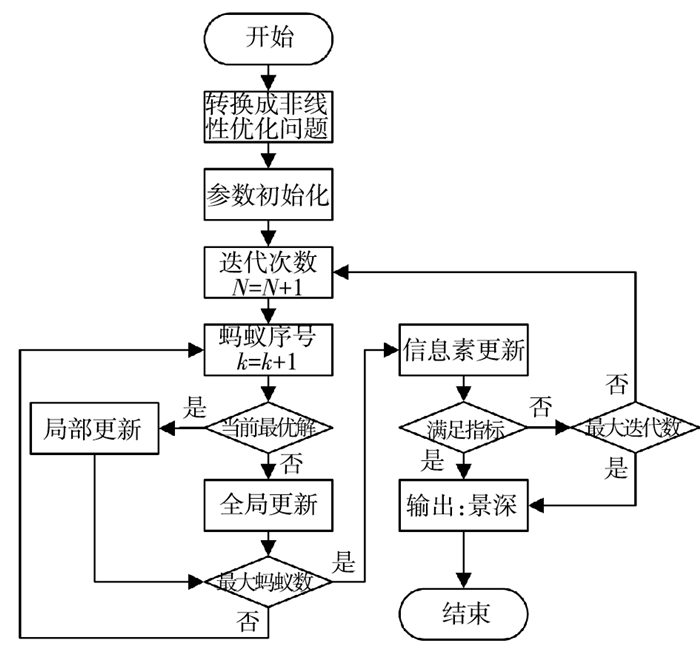
|
图 3 蚁群搜索算法流程 Figure 3 Ant colony search flow chart |
1) 将非线性方程组(9)转换为非线性优化问题.将式(9)定义为F(X)=[f1X), f2(X), f3(X)]T,那么优化目标为
| $ F{\rm{Best}}\left( \mathit{\boldsymbol{X}} \right) = \sum\limits_{i = 1}^3 {{{\left[ {{f_i}\left( \mathit{\boldsymbol{X}} \right)} \right]}^2}} . $ | (10) |
2) 设置初始参数.参数包括:蚁群大小k、最大迭代次数Nmax、搜索步长ω、各变量区间[Up,Low]、信息素强度Q、信息素启发因子α、信息素遗忘因子ρ、全局状态转移因子p等.由于初始景深未知,在第1次寻优时,各变量区间较大,所需蚁群规模较大,扩大搜索步长来减少计算时间.在之后的寻优过程中,考虑相对运动状态是连续变化的,将各变量区间设置为以上次寻优获得的最优解为中心的较小区间,并减小蚁群规模,以此减少计算时间.
3) 初始化蚂蚁位置和信息素浓度.每只蚂蚁在区间范围内随机选择初始位置,且初始信息素浓度选取公式为
| $ \tau \left( k \right) = \exp \left[ { - F{\rm{Best}}\left( {{\mathit{\boldsymbol{X}}_k}} \right)} \right]. $ | (11) |
由式(11)可知,τ(k)越大,其所对应的FBest(Xk)越小.将信息素浓度最大的蚂蚁所对应的解作为当前迭代过程的最优解,定义为
4) 局部更新.将当前迭代过程中为最优解的蚂蚁进行局部更新,更新公式为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{X}}\left( k \right) = \mathit{\boldsymbol{\tilde X}} + \omega \left( {1 - N/{N_{\max }}} \right),{\rm{rand}}\left( 1 \right) < 0.5;\\ \mathit{\boldsymbol{X}}\left( k \right) = \mathit{\boldsymbol{\tilde X}} - \omega \left( {1 - N/{N_{\max }}} \right),{\rm{rand}}\left( 1 \right) \ge 0.5. \end{array} \right. $ | (12) |
式中N为当前迭代次数.由式(12)可知,随着迭代次数的增加,局部搜索步长逐渐减小,当越靠近精确解时,局部更新就越缓慢,从而提高局部更新的稳定性.
5) 全局更新.将当前迭代过程中非最优解的蚂蚁进行全局更新,更新公式为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{X}}\left( k \right) = \mathit{\boldsymbol{X}}\left( k \right) + {\rm{rand}}\left( {3,1} \right) \cdot \left[ {\mathit{\boldsymbol{\tilde X}} - \mathit{\boldsymbol{X}}\left( k \right)} \right],\\ \;\;\;\;\;\;\;\;\;\;\;\;p > P\left( k \right);\\ \mathit{\boldsymbol{X}}\left( k \right) = \mathit{\boldsymbol{X}}\left( k \right) + \omega ,\;\;\;\;\;p \le P\left( k \right). \end{array} \right. $ |
其中全局转移概率P(k)的计算公式为
| $ P\left( k \right) = \exp \left[ {\tau \left( {\mathit{\boldsymbol{\tilde X}}} \right) - \tau \left( k \right)} \right]/\exp \left[ {\tau \left( k \right)} \right]. $ |
6)信息素更新.信息素更新与待优化的非线性函数有关,更新公式为
| $ \tau \left( k \right) = \left( {1 - \rho } \right)\tau \left( k \right) + \Delta \tau \left( k \right), $ |
其中Δτ(k)的选取按照蚁周(Ant-cycle)模型,其计算公式为
| $ \Delta \tau \left( k \right) = \left\{ \begin{array}{l} Q/F{\rm{Best}}\left( \mathit{\boldsymbol{X}} \right),F{\rm{Best}}{\left( \mathit{\boldsymbol{X}} \right)_{{\rm{now}}}} < F{\rm{Best}}{\left( \mathit{\boldsymbol{X}} \right)_{{\rm{before}}}};\\ 0,F{\rm{Best}}{\left( \mathit{\boldsymbol{X}} \right)_{{\rm{now}}}} \ge F{\rm{Best}}{\left( \mathit{\boldsymbol{X}} \right)_{{\rm{before}}}}. \end{array} \right. $ |
7) 输出全局最优解.设置优化指标提前结束迭代,或者达到最大迭代步数则迭代结束,然后输出存在测量误差情况下最满足三角形支架实际构型约束的景深值.
3.4 绝对定位方法已知景深dn(n=1, 2, 5),由式(8)求得Pc, n(n=1, 2, 5),还需要一个特征点的位置信息才能完成绝对定位解算.把三角形支架内切圆圆心作为第4个特征点,从3个已知顶点位置信息可以得到内切圆圆心在相机坐标系和目标体坐标系中的坐标,分别定义为Pc, 6和Pt, 6,由Pc, n(n=1, 2, 5, 6)和Pt, n(n=1, 2, 5, 6)通过绝对定位算法来解算相对位姿[15].
定义坐标位置误差为δp,由式(2)得
| $ \delta _p^2 = \sum {{{\left\| {{\mathit{\boldsymbol{P}}_{{\rm{c}},n}} - \left( {\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{P}}_{{\rm{t}},n}} + \mathit{\boldsymbol{T}}} \right)} \right\|}^2}} . $ | (13) |
通过最小化坐标位置误差来获得旋转矩阵R和位移矢量T,有定义:
| $ \begin{array}{l} \delta _p^2 = \sum {{{\left\| {{\mathit{\boldsymbol{Q}}_{{\rm{c}},n}} - \mathit{\boldsymbol{R}}{\mathit{\boldsymbol{Q}}_{{\rm{t}},n}}} \right\|}^2}} = \sum {\left( {\mathit{\boldsymbol{Q}}_{{\rm{c}},n}^{\rm{T}}{\mathit{\boldsymbol{Q}}_{{\rm{c}},n}} + } \right.} \\ \;\;\;\;\;\;\;\;\left. {\mathit{\boldsymbol{Q}}_{{\rm{t}},n}^{\rm{T}}{\mathit{\boldsymbol{Q}}_{{\rm{t}},n}} - 2\mathit{\boldsymbol{Q}}_{{\rm{c}},n}^{\rm{T}}\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{Q}}_{{\rm{t}},n}}} \right). \end{array} $ | (14) |
由式(14)可知,求解最小坐标误差也就是最大化为
| $ \begin{array}{l} F = \sum {\mathit{\boldsymbol{Q}}_{{\rm{c}},n}^{\rm{T}}\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{Q}}_{{\rm{t}},n}}} = {\rm{Trace}}\left( {\sum {\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{Q}}_{{\rm{t}},n}}\mathit{\boldsymbol{Q}}_{{\rm{c}},n}^{\rm{T}}} } \right) = \\ \;\;\;\;\;\;{\rm{Trace}}\left( {\mathit{\boldsymbol{RH}}} \right), \end{array} $ |
式中
定理 对于任意正定矩阵AAT和任意正交矩阵B,都存在Trace(AAT)≥Trace(BAAT)成立.对于奇异值分解H =UΛVT,其中:U、V分别为3×3阶正交矩阵;Λ为3×3阶非负对角矩阵.定义正交矩阵X= VUT,得XH = VUTUΛVT= VΛVT,其中VΛVT为正定对称矩阵.假设X= VUT不是所求旋转矩阵R,那么存在旋转矩阵(正交矩阵)B进行一次旋转变化,使得BX为所求旋转矩阵R.根据定理,有Trace(XH)≥Trace(BXH),所以X= VUT使得F=Trace(RH)最大化,即是所求旋转矩阵R.位移矢量T计算公式为
| $ \mathit{\boldsymbol{T}} = {\mathit{\boldsymbol{P}}_{\rm{c}}} - \mathit{\boldsymbol{R}}{\mathit{\boldsymbol{P}}_{\rm{t}}}. $ |
以在轨服务最终接近段为背景,考虑阻尼、液体晃动以及能量损耗等因素,失效航天器通常是围绕最大惯量主轴旋转,而绕着其他惯量主轴只有微小的晃动.假设失效目标航天器的外形几何构型已知.令两个航天器之间的相对状态为:Z轴相对姿态运动γ=π/18(t-10) rad,X、Y轴旋转只有微小晃动,并且按照3-2-1的旋转顺序;初始相对位置r=[0.1, 0.2, 2.0]T m,相对运动速度v=[0.005, 0.010, 0.100]T m/s.参考相对位姿如图 4所示.
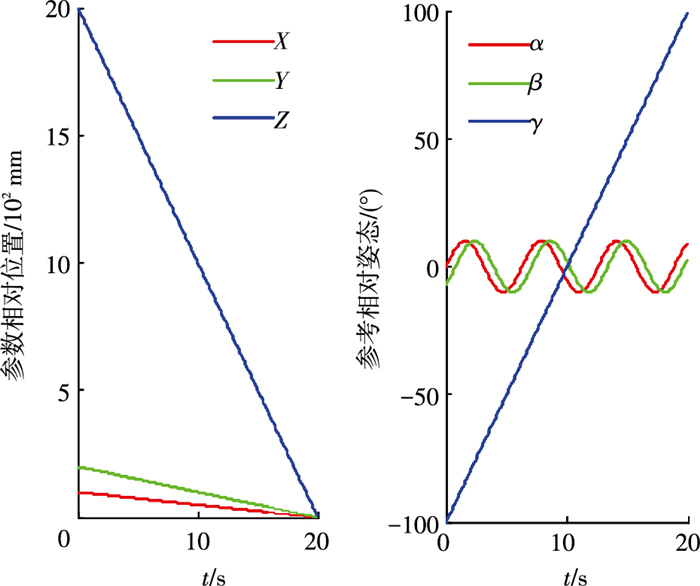
|
图 4 参考相对位姿 Figure 4 Reference relative position and attitude |
相机参数:焦距10 mm;敏感元件尺寸2/3″;分辨率1 280×1 024;像元大小12 μm×12 μm.
为了简化仿真过程而又不影响仿真结果,假设测量到线段Pt, 1Pt, 5和线段Pt, 2Pt, 5的1/5长度以及完整线段Pt, 1Pt, 2,如图 2中粗线部分.假设三角形支架顶点在目标体坐标系的坐标为:Pt, 1=[500, 500, 500]T mm,Pt, 2=[1500, 500, 500]T mm,Pt, 5=[1 000, 1 480, 500]T mm.考虑三角形支架的几何变形等误差,顶点坐标误差为±10 mm,特征提取误差为白噪声,噪声方差δx=δy=1.0个像素.
蚁群搜索算法的初始设置为:蚁群大小k=500只;最大迭代次数Nmax=10次;信息素强度Q=10;全局状态转移因子p=10;信息素启发因子α=1;信息素遗忘因子ρ=1.
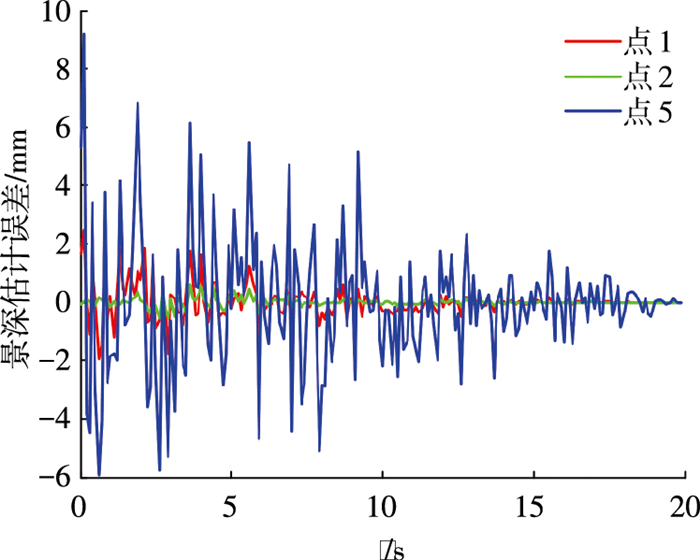
|
图 5 景深估计误差 Figure 5 Depth estimation error |
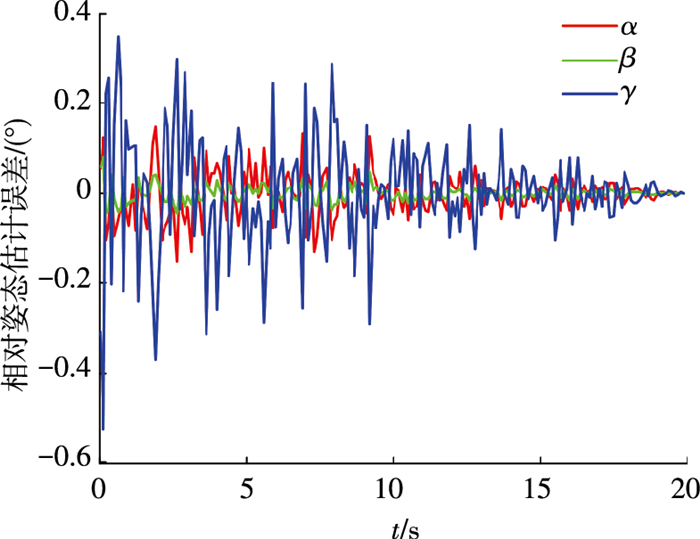
|
图 6 相对姿态估计误差 Figure 6 Relative attitude estimation error |
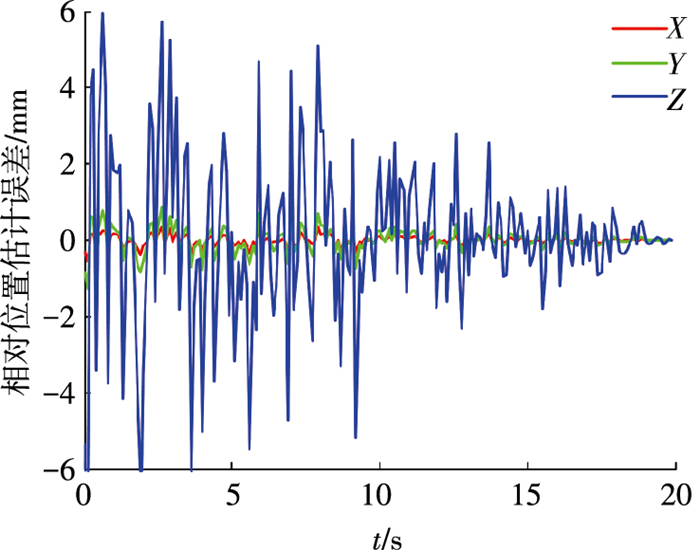
|
图 7 相对位置估计误差 Figure 7 Relative position estimation error |
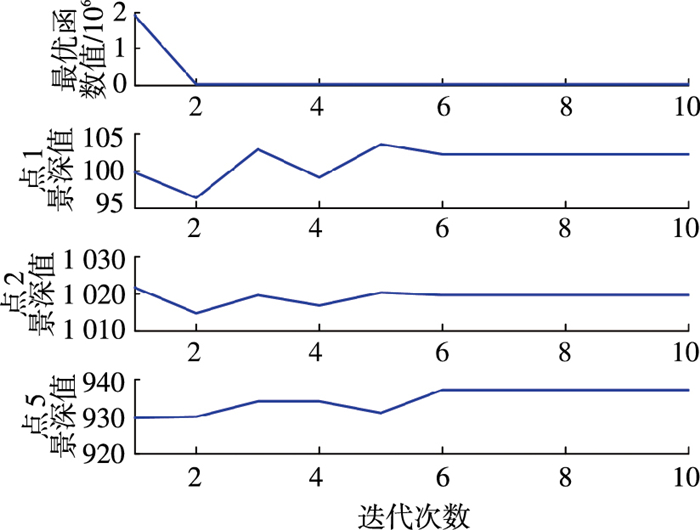
|
图 8 一次蚁群搜索迭代过程 Figure 8 One ant colony search iteration process |
由上述仿真结果可知,景深误差随着航天器间的相对距离的减小而逐渐减小.Pt, 5的景深误差较Pt, 1和Pt, 2大,是由于点Pt, 5是通过两条线段延长线交点而获得,包含了两条线段的测量误差.随着景深误差的减小,相对姿态估计误差和相对位置估计误差也相应减小.在整个过程中,相对姿态估计误差总体小于0.6°,相对位置估计误差总体小于6 mm.在相对距离小于1 m时,即仿真时间10 s后,相对姿态估计误差为0.2°,相对位置估计误差为3 mm.从蚁群搜索算法的迭代过程来看,在进行6次左右的迭代,就能找出最优解,使得目标函数值接近于0.
定义相对姿态估计平均误差为
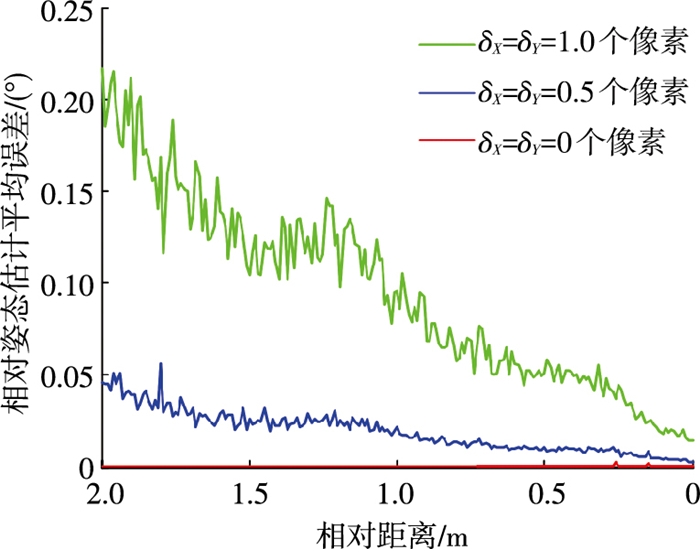
|
图 9 相对姿态估计平均误差(100次仿真) Figure 9 Relative attitude mean estimation error in 100 simulations |
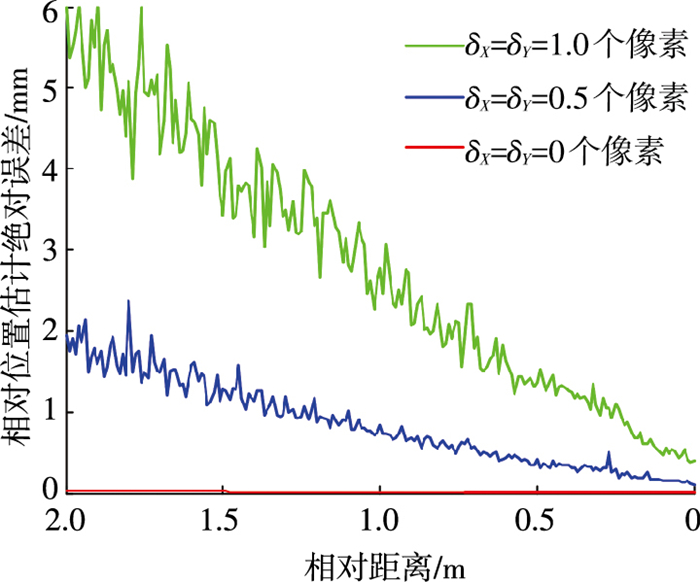
|
图 10 相对位置估计绝对误差(100次仿真) Figure 10 Relative position absolute estimation error in 100 simulations |
1) 在近距离接近阶段仅以太阳帆板三角形支架的部分结构为测量目标时,算法是有效的,能够得到较高精度的相对导航数据,在测量误差δx=δy=0.5个像素时,整个过程相对姿态估计平均误差小于0.05°,相对位置估计绝对误差小于2.5 mm.
2) 在接近非合作航天器的过程中,导航算法的景深估计误差随着航天器之间相对距离的减小而减小,而导航精度越来越高.
3) 导航算法在投影点测量误差较大时仍具有较高的精度,因此对投影点提取误差具有较好的鲁棒性.
| [1] |
王晓海. 空间在轨服务技术及发展现状与趋势[J].
卫星与网络, 2016(3): 70-76.
WANG Xiaohai. Development and trend of space on-orbit servicing technology[J]. Satellite & Network, 2016(3): 70-76. DOI: 10.3969/j.issn.1672-965X.2016.03.009 |
| [2] |
贾平, 刘海印, 李辉. 德国轨道任务服务系统发展分析[J].
中国航天, 2016(6): 24-29.
JIA ping, LIU Haiyin, LI Hui. Development of deutsche orbitale servicing mission[J]. Aerospace China, 2016(6): 24-29. |
| [3] |
曾占魁, 谷蔷薇, 曹喜滨. 基于正交Procrustes分析的航天器单目视觉相对位姿确定方法[J].
红外与激光工程, 2015, 44(s1): 113-118.
ZENG Zhankui, GU Qiangwei, CAO Xibin. Relative pose monocular vision determination of spacecraft using orthogonal Procrustes analysis[J]. Infrared and Laser Engineering, 2015, 44(s1): 113-118. DOI: 10.3969/j.issn.1007-2276.2015.z1.021 |
| [4] |
STOLL E, LETSCHNIK J, WALTER U, et al. On-orbit servicing[J].
IEEE Robotics & Automation Magazine, 2009, 16(4): 29-33.
DOI: 10.1109/MRA.2009.934819 |
| [5] |
于长安. 基于合作目标的单目视觉位姿跟踪技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2010.
YU Chang'an. Study on position and attitude tracking technology of single camera vision based on cooperate aim[D]. Harbin: Harbin Institute of Technology, 2010. |
| [6] |
曹彩秀. 非合作航天器位姿在轨测量方法的研究[D]. 北京: 北京邮电大学, 2015.
CAO Caixiu. Pose on-orbit measurement of non-cooperative spacescraft[D]. Beijing: Beijing University of Posts and Telecommunication, 2015. |
| [7] |
苗锡奎, 朱枫, 郝颖明, 等. 基于太阳能帆板部件的空间非合作飞行器视觉位姿测量方法[J].
高技术通讯, 2013, 23(4): 400-406.
MIAO Xikui, ZHU Feng, HAO Yingming, et al. Vision pose measurement for non-cooperative space vehicles based on solar panel component[J]. Chinese High Technology Letters, 2013, 23(4): 400-406. DOI: 10.3772/j.issn.1002-0470.2013.04.011 |
| [8] |
张鑫, 张雅声, 程文华, 等. 基于SoftPOSIT算法的单目视觉非合作目标相对位姿估计[J].
上海航天, 2016, 33(3): 124-129.
ZHANG Xin, ZHANG Yasheng, CHENG Wenhua, et al. Relative pose and attitude estimation for non-cooperative target by monocular camera based on Soft POSIT algorithm[J]. Aerospace Shanghai, 2016, 33(3): 124-129. DOI: 10.19328/j.cnki.1006-1630.2016.03.020 |
| [9] |
徐仙伟, 杨雁莹, 曹霁. 基于同心圆环模板的摄像机标定方法[J].
科学技术与工程, 2013, 13(31): 9375-9380.
XU Xianwei, YANG Yanying, CAO Ji. Camera calibration based on concentric ring template[J]. Science Technology and Engineering, 2013, 13(31): 9375-9380. DOI: 10.3969/j.issn.1671-1815.2013.31.042 |
| [10] |
谷蔷薇, 张世杰, 曾占魁, 等. 面向在轨服务的相对位姿单目视觉确定的凸松弛优化方法[J].
宇航学报, 2016, 37(6): 744-752.
GU Qiangwei, ZHANG Shijie, ZENG Zhankui, et al. A convex relaxation optimization method of on-orbit servicing pose estimation using monocular vision[J]. Journal of Astronautics, 2016, 37(6): 744-752. DOI: 10.3873/j.issn.1000-1328.2016.06.015 |
| [11] |
邓兴升, 孙虹虹, 汤仲安. 高斯牛顿迭代法解算非线性Bursa-Wolf模型的精度分析[J].
测绘科学, 2014, 39(5): 93-95.
DENG Xingsheng, SUN Honghong, TANG Zhong'an, et al. Precision of Gauss-Newton iterative algorithm for solving nonlinear Bursa-Wolf model[J]. Science of Surveying and Mapping, 2014, 39(5): 93-95. DOI: 10.16251/j.cnki.1009-2307.2014.05.017 |
| [12] |
杨柳, 陈艳萍. 求解非线性方程组的一种新的全局收敛的Levenberg-Marquardt算法[J].
计算数学, 2008, 30(4): 388-396.
YANG Liu, CHEN Yanping. A new globally convergent levenberg-marquardt method for solving nonlinear system of equations[J]. Mathematica Numerica Sinica, 2008, 30(4): 388-396. DOI: 10.3321/j.issn:0254-7791.2008.04.006 |
| [13] |
叶仕通, 万智萍. 一种基于改进全局信息素更新效率的蚁群算法及仿真[J].
计算机应用与软件, 2014, 31(1): 176-179.
YE Shitong, WAN Zhiping. An ant colony algorithm based on improving global pheromone update efficiency and its simulation[J]. Computer Applications and Software, 2014, 31(1): 176-179. DOI: 10.3969/j.issn.1000-386x.2014.01.046 |
| [14] |
STVTZLE T. Ant colony optimization[C]//Evolutionary Multi-Criterion Optimization. EMO 2009. Lecture Notes in Computer Science. Berlin, Heidelberg: Springer, 2009. DOI: 10.1007/978-3-642-01020-0_2.
|
| [15] |
ARUN K S, HUANG T S, BLOSTEIN S D. Least-squares fitting of two 3-D point sets[J].
IEEE Transactions on Pattern Analysis & Machine Intelligence, 1987, 9(5): 698-700.
DOI: 10.1109/TPAMI.1987.4767965 |
 2017, Vol. 49
2017, Vol. 49


