2. 中国直升机设计研究所,江西 景德镇 333000
2. China Helicopter Research and Development Institute, Jingdezhen 333000, Jiangxi, China
直升机近地悬停时,地面的干扰使旋翼桨盘平面内的轴向诱导速度减小,导致在相同的需用功率下旋翼的拉力较远离地面时有所增加,这种现象被称为地面效应(In ground effect,IGE)[1].对于共轴双旋翼直升机,由于上、下旋翼之间本身也存在严重的气动干扰现象,使共轴双旋翼的地面效应更加复杂,与常规单旋翼直升机的地面效应相比发生显著变化.因此,共轴双旋翼地面效应的研究对共轴式直升机的使用和设计具有重要意义.
大量的研究人员对单旋翼地面效应现象进行了广泛的研究.Duwalt[2]首先发展了一种用于前飞状态地面效应的自由尾迹模型.Curtiss等[3-4]和Lee等[5]基于自由尾迹模型运用镜像法求解地面效应中前飞旋翼的流场.近年来,辛冀等[6-8]针对单旋翼地面效应问题进行了深入的研究.
与单旋翼相比,共轴双旋翼上、下旋翼之间本身存在严重的干扰现象[9-11],近地面悬停时,上、下旋翼及地面三者之间复杂的干扰现象成为共轴双旋翼地面效应研究的焦点.Kang等[12-13]以动量源方法模拟旋翼对流场的作用,通过求解雷诺平均N-S方程得到地面效应中前飞横列式、纵列式和共轴双旋翼的流场形态.但对共轴双旋翼地面效应的进一步研究,如离地高度与拉力的关系,由于附加了上、下旋翼的扭矩配平条件,用CFD计算双旋翼地面效应的离地高度与拉力关系受计算机资源与时间限制.Griffiths等[14]发展了一套能用于分析双旋翼地面效应的自由尾迹模型,详细研究了横列式双旋翼的地面效应尾迹形态,但并没有给出共轴双旋翼的地面效应.覃燕华等[15]用自由尾迹方法计算了地面效应下的共轴双旋翼流场及诱导速度,但尚未分析共轴双旋翼的性能及其随不同离地高度的变化.
本文首先建立了用于共轴双旋翼地面效应分析的自由尾迹模型.其中,采用升力面法模拟桨叶对流场的作用,并用稳定性较好的三阶精度时间步进数值计算格式进行桨叶尾迹计算,引入地面面元法模拟地面对双旋翼流场的作用,根据已有的试验数据对共轴双旋翼无地效状态和单旋翼在地面效应下的计算结果进行对比验证.在此基础上,给出共轴双旋翼在不同离地高度下的尾迹与流场形态,分析诱导速度在上、下旋翼桨叶上的分布及构成,计算地面效应下共轴双旋翼的拉力系数,并对比共轴双旋翼与同实度单旋翼的拉力增益得出结论.
1 数值计算模型 1.1 共轴双旋翼自由尾迹模型为精确捕捉桨叶对流场的影响,本文以升力面模型[16-17]模拟桨叶的气动特性.在旋翼桨叶的展向和弦向上同时分段划分网格,在划分后的网格单元上布置桨叶附着涡,图 1中ψ表示桨叶方位角,ζ表示桨尖涡寿命角,Δζ表示桨尖涡寿命角的离散步长(如图 1所示).

|
图 1 桨叶升力面模型及自由尾迹模型 Figure 1 Blade lifting surface model and free-wake model |
根据模型要求,附着涡由四边形涡环或涡格来表示.中弧面上每个网格上放置一个涡格,涡格的前缘展向附着涡位于该网格的1/4弦线,弦向附着涡位于网格沿展向的分界线,涡格的后缘附着涡位于弦向相邻网格的1/4弦线.取每个格子中央弦线的3/4点为控制点,在该点处要求计算得到的流场合速度满足不可穿透条件:
| $ \nabla \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \cdot \mathit{\boldsymbol{n}} = 0. $ |
式中:Φ为控制点处流场的合速度势,n为控制点处的法向单位向量.
桨叶后缘各涡板会拖出尾随涡线,形成近尾迹.桨叶后缘脱出的尾迹在转过大约30°~60°寿命角后聚合并卷起成单根的桨尖涡线,形成远尾迹.本文以直涡元离散桨尖涡线,以离散的桨叶方位角ψ和节点寿命角ζ对涡线节点进行编号,如图 1所示.
尾迹涡线按照当地速度在空间自由运动发展,对应的节点运动方程为
| $ \frac{{\partial \mathit{\boldsymbol{r}}\left( {\psi ,\zeta } \right)}}{{\partial \psi }} + \frac{{\partial \mathit{\boldsymbol{r}}\left( {\psi ,\zeta } \right)}}{{\partial \zeta }} = \frac{1}{\mathit{\Omega }} \cdot \mathit{\boldsymbol{u}}\left( {\psi ,\zeta } \right). $ | (1) |
式中:r(ψ, ζ)为涡线节点坐标,u(ψ, ζ)为节点处的诱导速度.以下为了书写方便,将表示节点位置的(ψ, ζ)省略.对于地面效应下的共轴双旋翼系统,节点的诱导速度为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{u}}_u} + {\mathit{\boldsymbol{u}}_l} + {\mathit{\boldsymbol{u}}_g} + {\mathit{\boldsymbol{u}}_\infty },\\ {\mathit{\boldsymbol{u}}_u} = {\mathit{\boldsymbol{u}}_{ub}} + {\mathit{\boldsymbol{u}}_{uf}},\\ {\mathit{\boldsymbol{u}}_l} = {\mathit{\boldsymbol{u}}_{ub}} + {\mathit{\boldsymbol{u}}_{lf}}. \end{array} \right. $ |
式中:uu为上旋翼在节点处的诱导速度,包含上旋翼桨叶附着涡引起的诱导速度uub和自由尾迹引起的诱导速度uuf;ul为下旋翼在节点处的诱导速度,包含下旋翼桨叶附着涡引起的诱导速度ulb和自由尾迹引起的诱导速度ulf;ug为地面面元在节点处的诱导速度;u∞为自由来流速度,各诱导速度项可由Biot-Savart定理求得.
本文采用一种稳定性较好的三阶精度时间步进数值计算格式(CB3D)[18]对式(1)的尾迹运动方程进行时间步进计算为
| $ \begin{array}{l} \frac{{{\mathit{\boldsymbol{r}}_{l + 1,k + 1}} - {\mathit{\boldsymbol{r}}_{l,k}}}}{{\Delta \psi }} = \frac{1}{\mathit{\Omega }}\left[ {\frac{1}{2}\left( {3\mathit{\boldsymbol{u}}\left( {{\mathit{\boldsymbol{r}}_{l,k}}} \right) - u\left( {{\mathit{\boldsymbol{r}}_{l - 1,k - 1}}} \right)} \right)} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{5}{{12}} \cdot \frac{1}{\mathit{\Omega }}\left( {{\mathit{\boldsymbol{u}}_{l,k + 1}} - 2{\mathit{\boldsymbol{u}}_{l - 1,k + 1}} + {\mathit{\boldsymbol{u}}_{l - 2,k + 1}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{5}{6} \cdot \frac{1}{\mathit{\Omega }}\left( {{\mathit{\boldsymbol{u}}_{l,k}} + {\mathit{\boldsymbol{u}}_{l - 1,k - 1}} - {\mathit{\boldsymbol{u}}_{l - 1,k}} - {\mathit{\boldsymbol{u}}_{l,k - 1}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{3} \cdot \frac{1}{\mathit{\Omega }}\left( {{\mathit{\boldsymbol{u}}_{l,k + 1}} - 2{\mathit{\boldsymbol{u}}_{l,k}} + {\mathit{\boldsymbol{u}}_{l,k - 1}}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{\gamma }{2}\left( {{\mathit{\boldsymbol{r}}_{l + 1,k + 1}} - 2{\mathit{\boldsymbol{r}}_{l + 1,k}} + {\mathit{\boldsymbol{r}}_{l + 1,k - 1}} + {\mathit{\boldsymbol{r}}_{l,k + 1}} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {2{\mathit{\boldsymbol{r}}_{l,k}} + {\mathit{\boldsymbol{r}}_{l,k - 1}}} \right). \end{array} $ |
式中:下标(l, k)为第l个方位角处桨叶拖出的涡线上第k个离散节点;γ的选取以“既确保格式数值稳定,又不会导致尾迹结构出现严重的非物理偏差”为原则[18].
1.2 地面模型本文采用在地面布置均布源面元的方法模拟地面对旋翼的影响.地面面元的源强度使面元控制点的法向速度为0,满足地面的不可穿越条件为
| $ {\mathit{\boldsymbol{V}}_g} = {\mathit{\boldsymbol{V}}_p} + {\mathit{\boldsymbol{V}}_{ub}} + {\mathit{\boldsymbol{V}}_{lb}} + {\mathit{\boldsymbol{V}}_{uf}} + {\mathit{\boldsymbol{V}}_{lf}} + {\mathit{\boldsymbol{V}}_\infty }. $ | (2) |
从式(2)可以看出,地面各控制点的诱导速度受到地面上其他面元Vp、上下桨叶的附着涡Vub和Vlb、上下旋翼的尾迹Vuf和Vlf以及自由来流V∞对其的影响.由不可穿越边界条件可得地面面元的强度.
为避免在迭代计算过程中出现部分涡线落入地面以下导致不收敛的问题,在迭代过程中采用“等体积”修正法[6]修正落入地面以下的涡线.修正后的节点高度计算公式如下
| $ \left\{ {\begin{array}{*{20}{l}} {{h_{{\rm{new}}}} = \frac{{{h_{{\rm{last}}}} \cdot {r_{{\rm{last}}}}}}{{{r_{{\rm{origin}}}}}},}\\ {{z_{{\rm{new}}}} = {h_{{\rm{new}}}} + {z_g}.} \end{array}} \right. $ |
式中:hnew为修正后节点所在“气团”的高度;hlast、rlast分别为这一步迭代开始时的“气团”厚度和半径;rorigin为这一步迭代结束但未修正时的“气团”半径;zg为地平面的轴向坐标;znew为修正后的节点轴向坐标.
1.3 共轴双旋翼配平在地面效应研究中,为获得在一定功率下的拉力增益TIGE/TOGE,悬停地面效应下的共轴双旋翼系统必须进行配平满足以下两个条件.
1) 功率平衡.在分析共轴双旋翼离地面不同高度的拉力变化时,旋翼系统的需用功率保持不变.
2) 扭矩平衡.共轴双旋翼的上、下旋翼处于同一轴线,两旋翼旋转方向相反,反扭矩互相抵消,此时直升机的偏航力矩为零.
对于悬停的共轴双旋翼系统,定义操纵输入矢量为
| $ \mathit{\boldsymbol{x}} = {\left( {\theta _{0.7}^u,\theta _{0.7}^l} \right)^{\rm{T}}}, $ |
输出响应矢量为
| $ \mathit{\boldsymbol{y}} = {\left( {C_P^{tw},C_Q^{tw}} \right)^{\rm{T}}}, $ |
式中:θ0.7u、θ0.7l分别为上、下旋翼的总距角;CPtw、CQtw分别为两旋翼的功率和扭矩之和.为便于求解,对于操纵矢量进行泰勒级数展开至一阶并简化得到
| $ \Delta \mathit{\boldsymbol{x}} = {\left[ \mathit{\boldsymbol{J}} \right]^{ - 1}} \cdot \left[ \begin{array}{l} C_P^{tw} - C_{{P_{obj}}}^{tw}\\ C_Q^{tw} - 0 \end{array} \right], $ |
其中[J]为雅克比矩阵.
| $ \left[ \mathit{\boldsymbol{J}} \right] = \frac{{\partial y}}{{\partial x}} = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial C_P^{tw}}}{{\partial \theta _{0.7}^u}}}&{\frac{{\partial C_P^{tw}}}{{\partial \theta _{0.7}^l}}}\\ {\frac{{C_Q^{tw}}}{{\partial \theta _{0.7}^u}}}&{\frac{{C_Q^{tw}}}{{\partial \theta _{0.7}^l}}} \end{array}} \right]. $ |
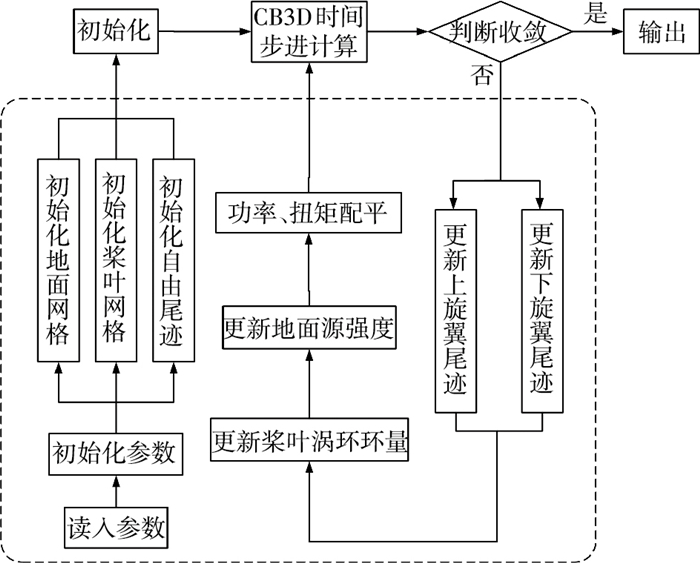
共轴双旋翼悬停地面效应的自由尾迹计算流程如图 2所示,其具体过程如下:1)给定旋翼参数及飞行状态,初始化计算参数、地面网格、桨叶网格和尾迹涡线.2)对共轴双旋翼尾迹使用CB3D三阶时间步进格式进行迭代.每次迭代计算完成后,更新桨叶涡环环量和地面源强度.求解共轴双旋翼悬停地面效应配平方程.3)求计算所得的功率和扭矩与目标值的差值,如果满足收敛条件进入步骤4);否则回到步骤2).4)输出计算结果.
|
图 2 共轴双旋翼地面效应计算流程 Figure 2 Flow chart of coaxial rotor in ground effect |
有关共轴双旋翼地面效应的试验数据还未见发表,本文采用已发表的无地面效应下共轴双旋翼的诱导速度分布和地面效应下单旋翼的尾迹结构和拉力增益曲线验证本文模型.
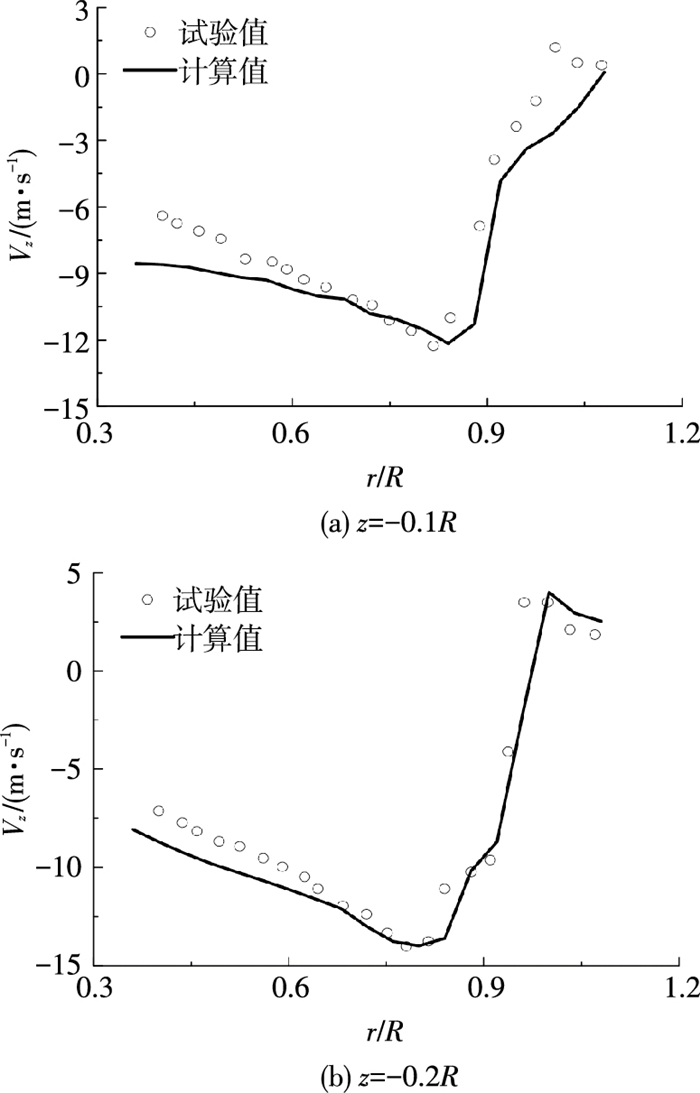
2.1 共轴双旋翼诱导速度验证图 3为使用本文模型计算的在上旋翼下方0.1R和0.2R处的轴向诱导速度分布与试验数据[19]的对比.所用的旋翼模型是两副相同的铰接式双叶旋翼,翼型为NACA0012,无预扭,旋翼半径为945 mm,弦长76 mm,上、下旋翼的转速皆为1 200 r/min,双旋翼相距0.185R,上旋翼总距为9°,下旋翼总距为10.27°,其他参数详见文献[19].由于流管收缩与桨尖损失,轴向诱导速度的极值点位置小于1.0R,且随着|z|的增大,诱导速度增大.由图 3可见,计算结果与试验值的变化趋势和大小基本吻合.
|
图 3 共轴双旋翼下方不同位置处轴向诱导速度分布 Figure 3 Induced velocity distribution below coaxial rotor at different axial distances |
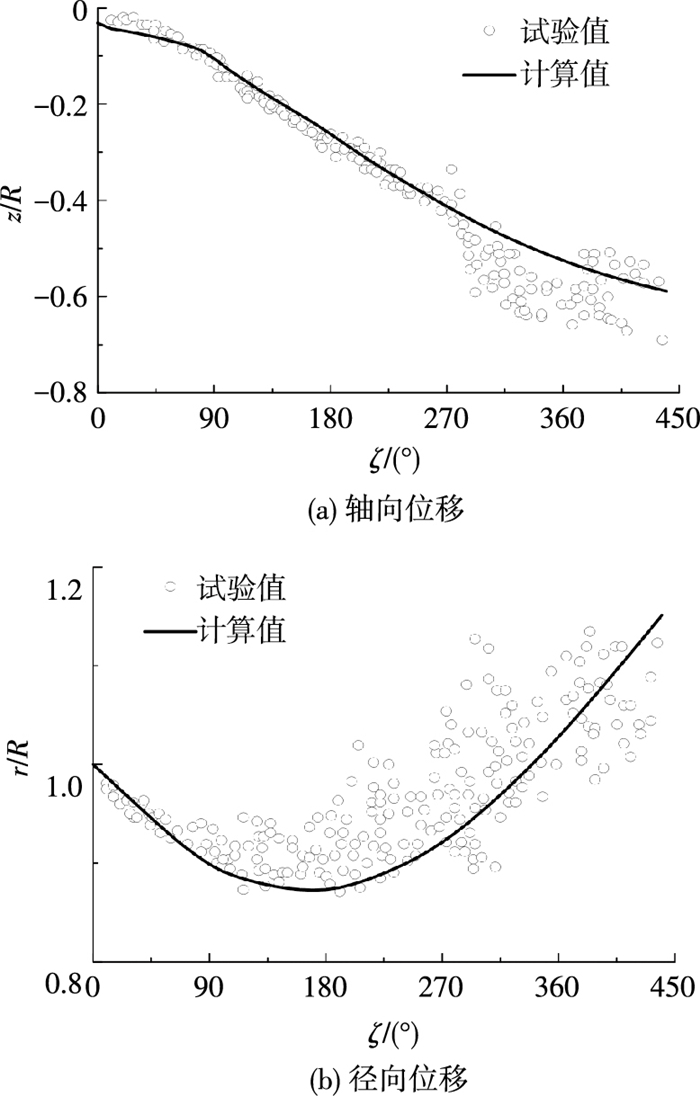
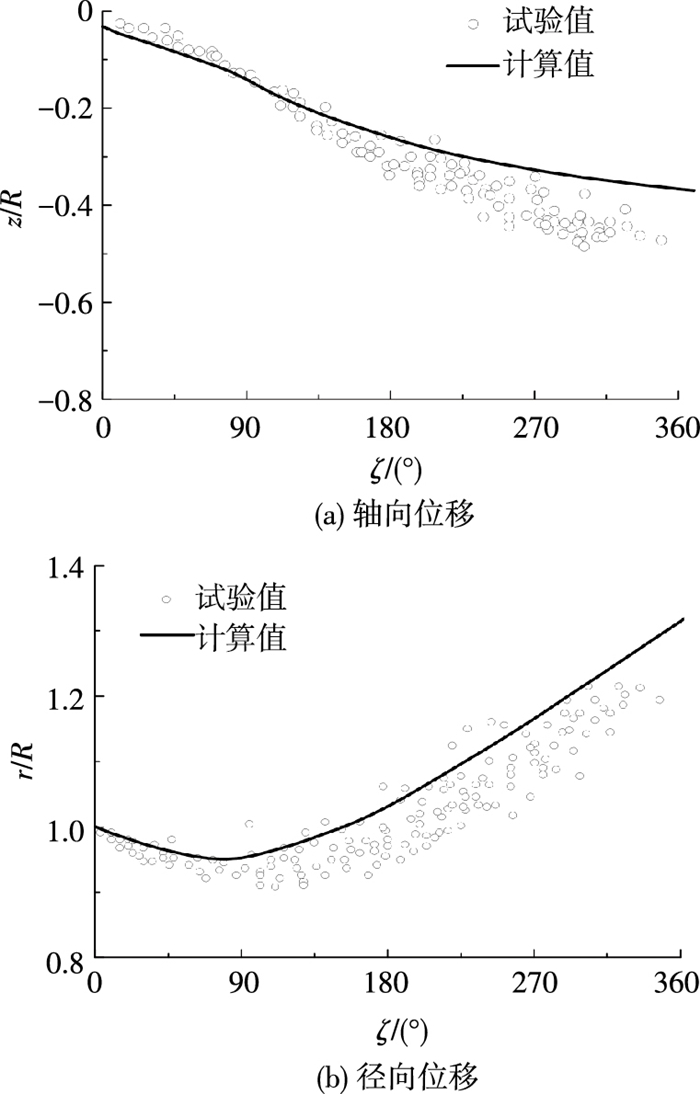
图 4、5为旋翼在不同离地高度下,计算得到的旋翼桨尖涡线的轴向位置、径向位置与试验值[20]的对比,其中的拉力系数按试验结果给定.使用的模型旋翼半径为1.105 m,弦长为0.18 m,旋翼转速为1 645 r/min,其他参数详见文献[20].由图 4、5可知,随着旋翼高度的下降,桨尖涡线的轴向速度变慢,径向向外扩张的位移变大,计算得到的桨尖涡线位置同试验数据符合较好.
|
图 4 h=0.84R时桨尖涡线位置随寿命角的变化(CT/σ=0.071) Figure 4 Variation of tip vortex IGE, h=0.84R, CT/σ=0.071 |
|
图 5 h=0.52R时桨尖涡线位置随寿命角的变化(CT/σ=0.09) Figure 5 Variation of tip vortex IGE, h=0.52R, CT/σ=0.09 |
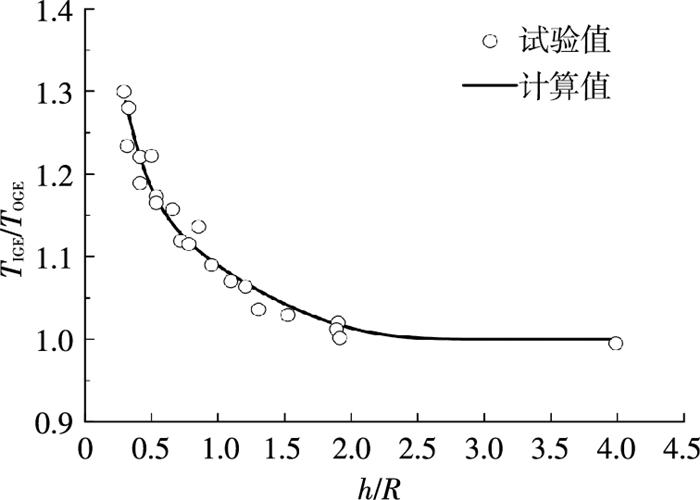
图 6为旋翼在恒定功率下,计算所得的拉力增益曲线与试验[20]的对比图.试验结果表明,在恒定功率下,当旋翼离地高度小于2.0R时旋翼拉力增大,出现较明显的地面效应现象,且随着高度降低拉力的增长率变大.图 6计算结果与试验值符合较好,由此可知本文的方法可用于模拟地面效应下旋翼拉力的增长.
|
图 6 功率不变时旋翼拉力增益随高度的变化 Figure 6 Thrust coefficient in different height at constant power |
本文在无地面效应共轴双旋翼的验证中考虑了上、下旋翼间的干扰,忽略了地面影响;在单旋翼的验证中考虑了地面影响,忽略了旋翼间的干扰.将两者的验证结果结合,说明本文模型既能反映上、下旋翼的干扰,也能验证地面对旋翼系统的影响.因此,使用模型进行共轴双旋翼地面效应的分析.
3 共轴双旋翼地面效应分析用于计算分析的共轴双旋翼模型的每副旋翼由2片矩形桨叶构成,翼型为NACA0012,旋翼半径为2 m,旋翼展弦比为10.0,旋翼根切为0.21R,实度为0.1,桨叶负扭转为10°,旋翼转速为93.5 rad/s,两副旋翼高度差为0.2R,给定共轴双旋翼系统的功率系数为Cp/σ=0.015.进行迭代计算时,尾迹迭代圈数为5,时间和空间的离散角度为Δψ=Δζ=10°.
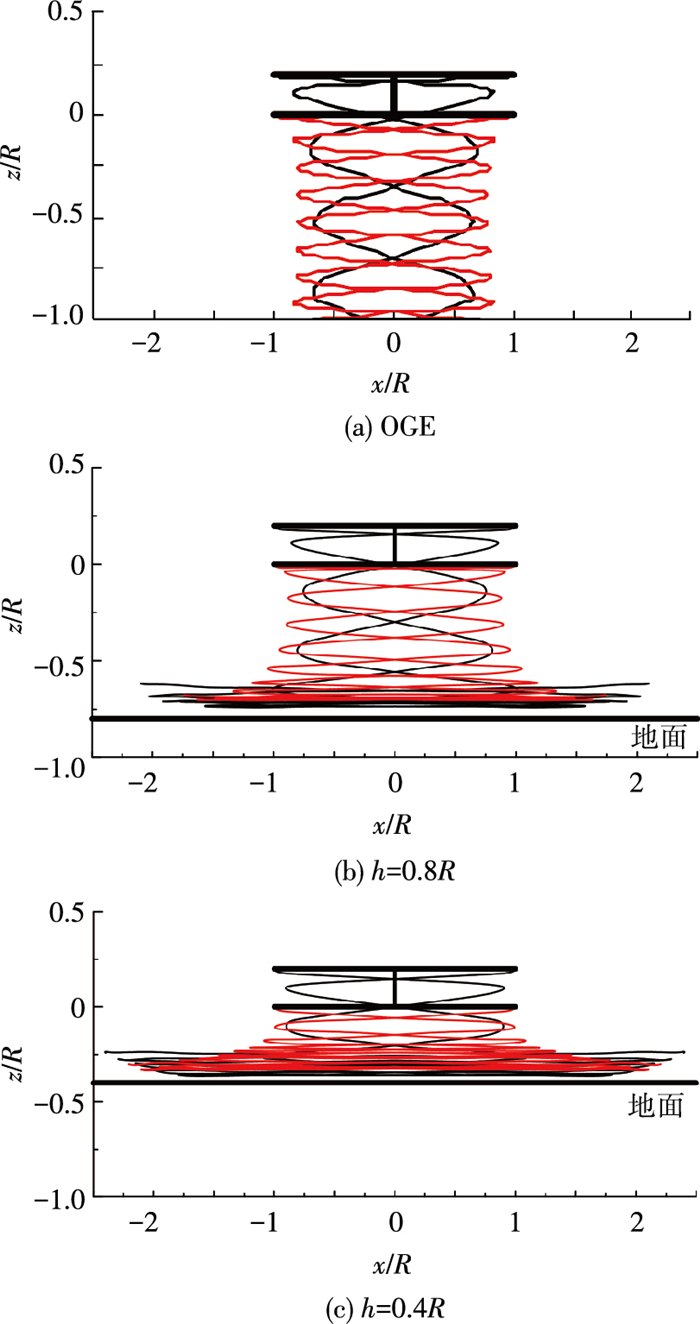
3.1 尾迹与流场图 7给出了在无地效(OGE)和下旋翼离地高度h=0.8R、h=0.4R时共轴双旋翼的尾迹涡线图.由图 7可知,地面效应使旋翼尾迹涡线向上卷起,下旋翼桨尖涡的卷起高度大于上旋翼.这是因为上旋翼尾迹的轴向运动速度大于下旋翼,因此其涡线先一步撞击地面,这部分气流发生减速,在与下旋翼涡线发生干扰作用后,下旋翼涡线便在还未接触地面时就开始卷起.
|
图 7 共轴双旋翼桨尖涡线图(无地效, h=0.8R, h=0.4R) Figure 7 Tip vortex geometry of coaxial rotor, OGE, h=0.8R, h=0.4R |
图 7还可以看到,地面效应使桨尖涡在地面附近发生径向扩张,随着旋翼高度的降低,扩张趋势更明显.这是由于低速流场的气体具有不可压缩性,旋翼高度的降低使其下方气团被压缩发生径向膨胀.
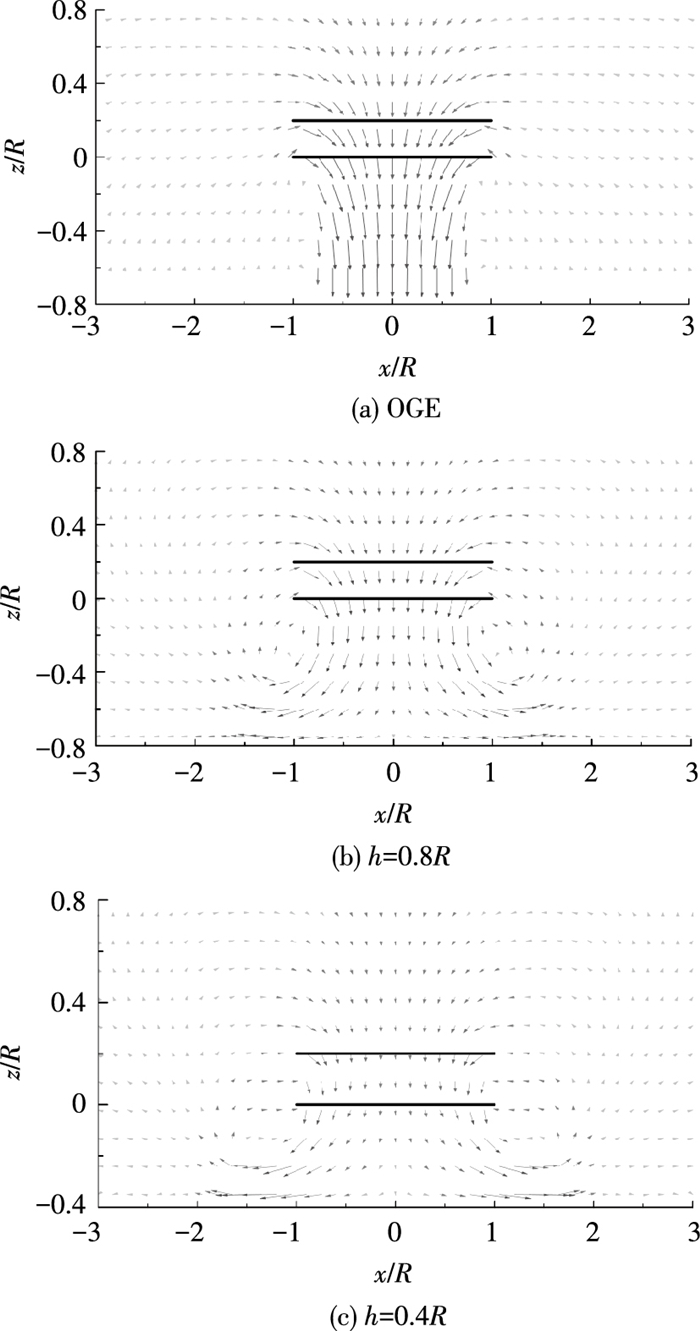
图 8给出了无地效、h=0.8R和h=0.4R时共轴双旋翼纵向剖面诱导速度矢量图.地面效应时,由于近地面气团的径向扩张,地面附近的径向诱导速度增大.图 8所示在径向位置1~2倍半径处存在一个中心速度很小的涡环,随着旋翼高度降低,涡环中心位置受地面的影响,逐渐向旋翼桨盘平面移动.h=0.4R时,由于下旋翼离地面较近,其桨盘附近诱导速度分布变化较大,桨尖处的轴向诱导速度增大.
|
图 8 共轴双旋翼纵向剖面诱导速度矢量(无地效, h=0.8R, h=0.4R) Figure 8 Induced velocity vector of coaxial rotor in longitudinal cross section, OGE, h=0.8R, h=0.4R |
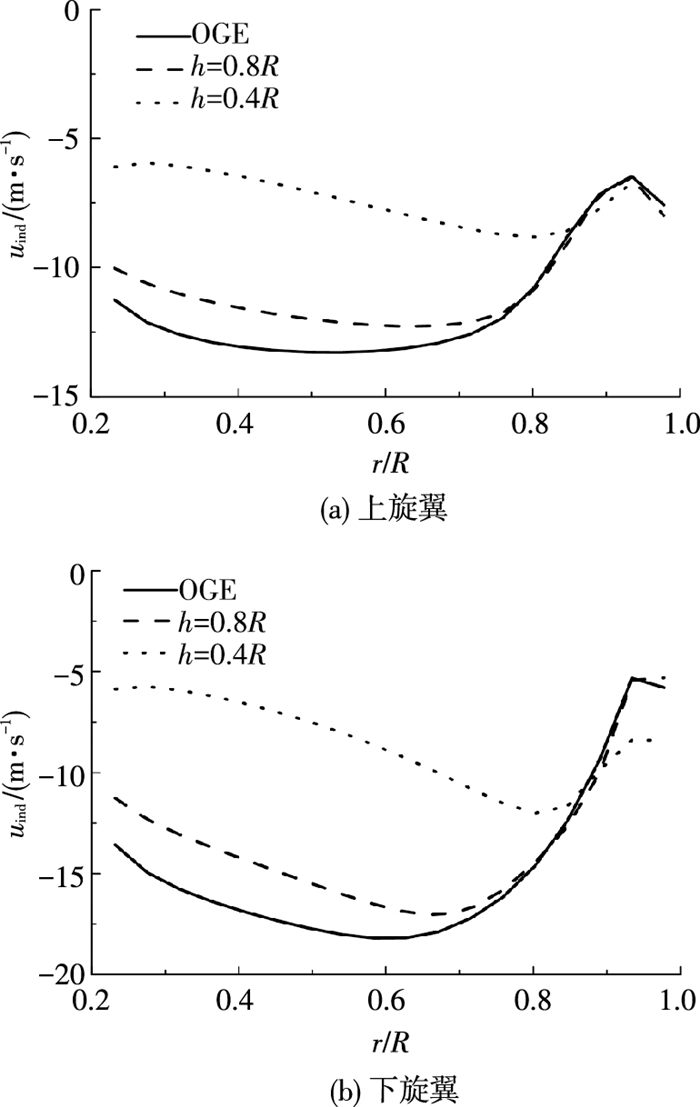
图 9为无地效、h=0.8R和h=0.4R时上、下旋翼轴向诱导速度分布的变化图.由图 9可知,由于地面的存在阻碍了气流向下运动,因此旋翼离地面越近,气流下洗速度越小.同时,随着旋翼高度的降低,桨盘诱导速度的分布更均匀,这将导致旋翼诱导功率减小.由尾迹与流场可知,当旋翼高度降低,涡环向旋翼方向移动,使旋翼桨尖下洗速度增大,从而使上、下旋翼的诱导速度分布更均匀.
|
图 9 轴向诱导速度在不同高度对比 Figure 9 Axial induced velocity in different height |
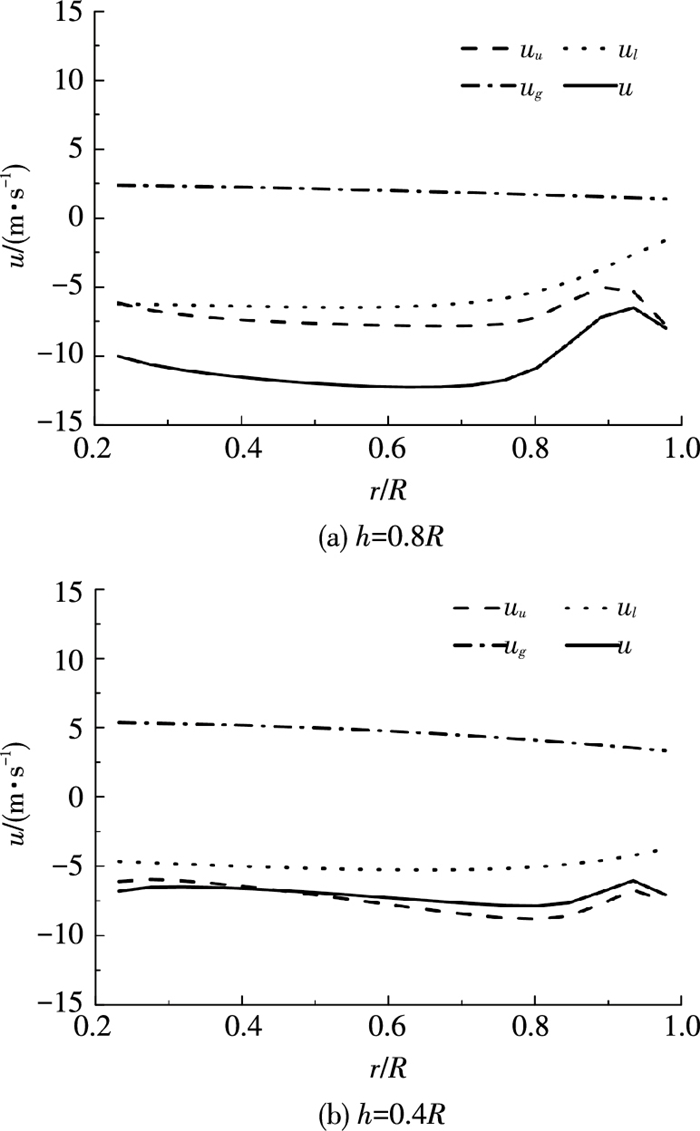
图 10为h=0.8R和h=0.4R时,上旋翼桨盘处的诱导速度及其分量在桨叶径向的分布图.地面效应悬停状态下的共轴双旋翼系统,在上旋翼桨盘某处的诱导速度u,分别由上旋翼(附着涡及自由尾迹)对此处的诱导速度uu、下旋翼(附着涡及自由尾迹)对此处的诱导速度ul及地面对此处的诱导速度ug构成.由图 10可知,随着旋翼高度的降低在上旋翼桨盘处,由上旋翼引起的诱导速度uu变化不明显;由下旋翼引起的诱导速度ul的绝对值略有减小,下洗作用减弱;由地面引起的诱导速度ug增大,对上旋翼桨盘的上洗作用增大,使得合诱导速度u的绝对值减小,且由于ug在桨盘平面的径向分布较均匀,使得地面效应下u的分布也更均匀(如图 9).
|
图 10 上旋翼诱导速度及其分量 Figure 10 Induced velocity and components of upper rotor |
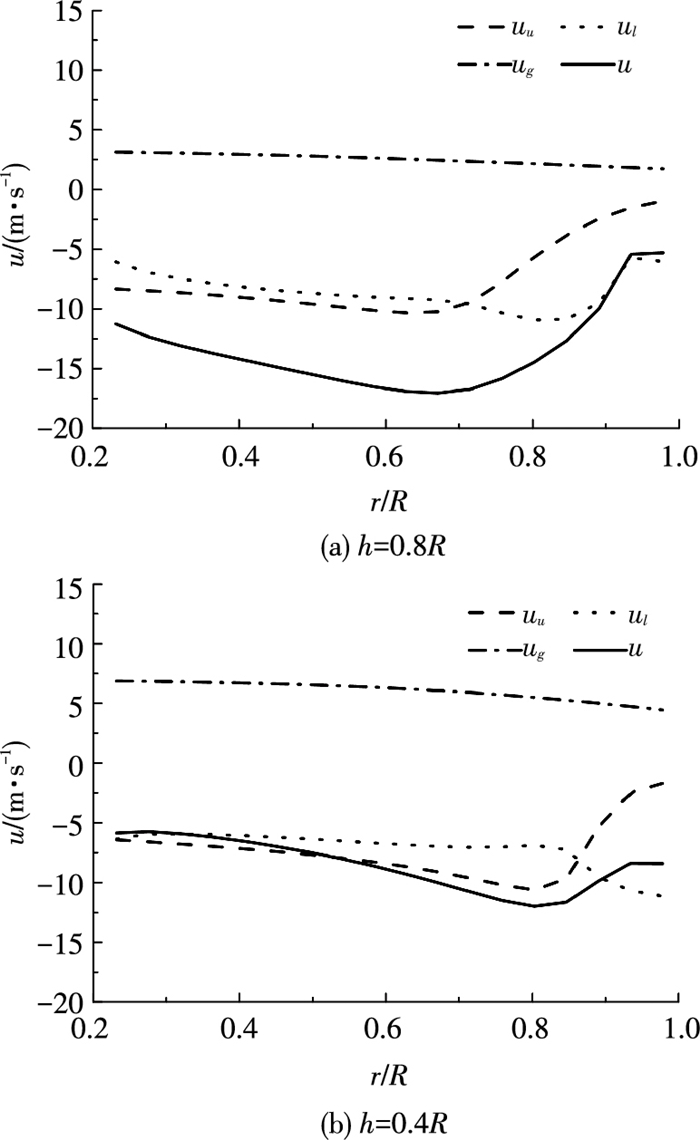
图 11为h=0.8R和h=0.4R时,下旋翼桨盘处的诱导速度及其分量在桨叶径向的分布图.下旋翼桨盘处诱导速度的构成与上文所述的上旋翼桨盘处诱导速度相同.但是,当旋翼高度降低,由上旋翼(附着涡及自由尾迹)对下旋翼桨盘引起的诱导速度uu有明显的外扩趋势.h=0.8R时,uu的最大下洗速度出现在r=0.65R处,而h=0.4R时,uu的最大下洗速度出现在r=0.8R处,这与图 8所示一致:桨尖涡线径向扩张,导致上旋翼尾迹与下旋翼桨盘平面的重叠面积增大,因此下旋翼受上旋翼的干扰范围扩大[21].
|
图 11 下旋翼诱导速度及其分量 Figure 11 Induced velocity and components of lower rotor |
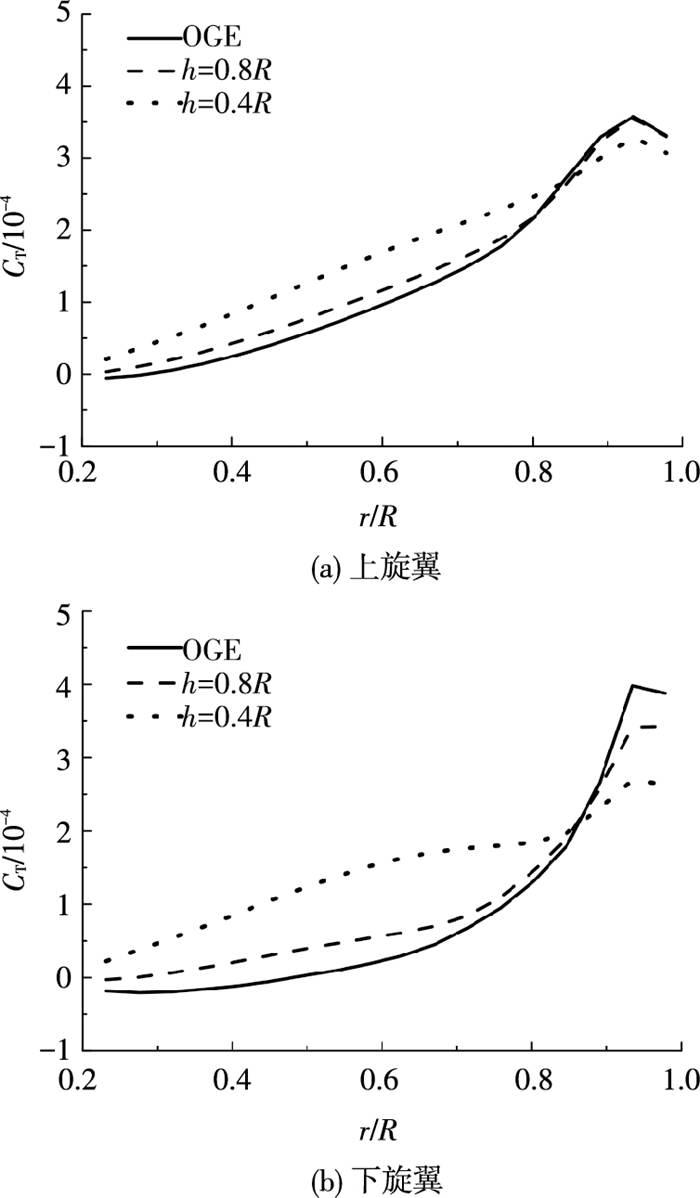
图 12为无地效、h=0.8R和h=0.4R时上、下旋翼拉力沿桨叶径向的分布图.由图 12可知,由于上、下旋翼桨盘处的下洗速度随着旋翼高度降低而减小(如诱导速度分析所述),有效迎角增大,导致地面效应下的旋翼拉力增大.图 12还可看出,随着旋翼高度的降低,拉力在上、下旋翼桨叶上的分布更均匀,这将改善旋翼的气动性能,使桨榖力矩减小,降低上、下旋翼发生碰撞的可能性.
|
图 12 上、下旋翼拉力在不同高度分布 Figure 12 Trust distribution of upper and lower rotor in different height |
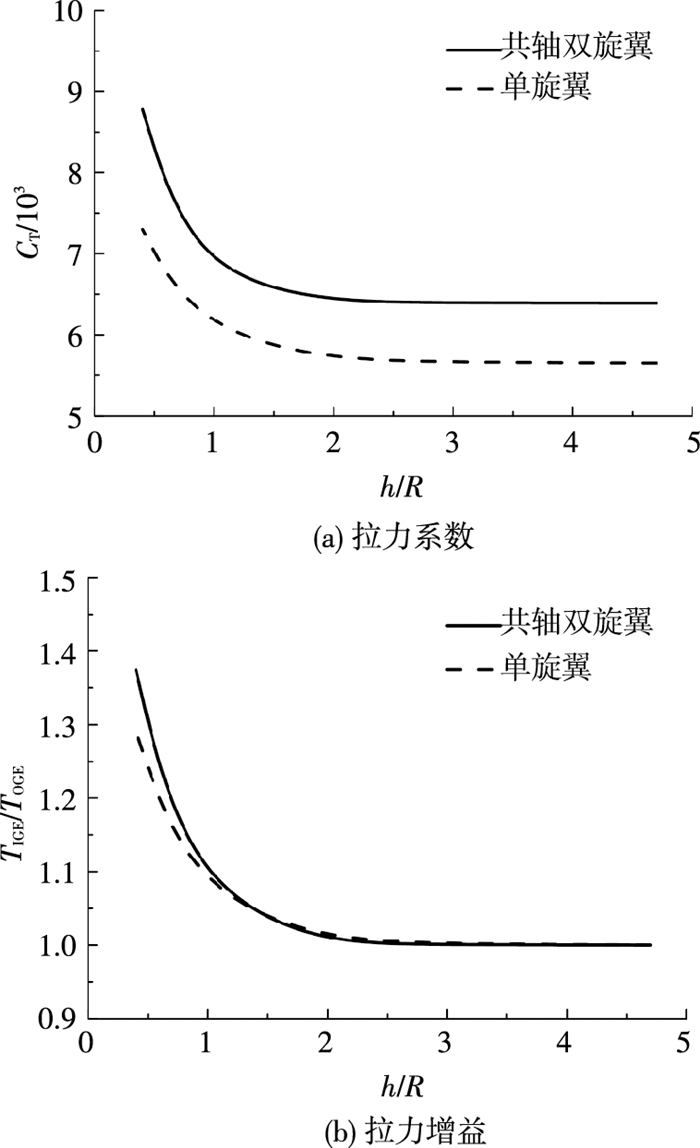
图 13为地面效应下共轴双旋翼与单旋翼(4片桨叶)的拉力系数及拉力增益曲线,其中单旋翼与共轴双旋翼具有相同桨叶外形、实度与功率系数.由图 13可知,离地面同等高度时,共轴双旋翼的拉力系数大于同实度单旋翼的拉力系数,且共轴双旋翼的拉力增益大于同实度单旋翼的拉力增益.根据能量守恒定律,旋翼的旋转动能转化为空气的周向与轴向运动动能,由于共轴双旋翼的上、下旋翼转向相反,空气的周向运动被削弱,导致共轴双旋翼下方空气的轴向运动动能更大.旋翼下方空气的轴向运动对旋翼产生反作用力,即为旋翼拉力,因此共轴双旋翼的拉力大于同实度的单旋翼.同时,较大的轴向下洗作用使地面受到更大的撞击作用,为了满足不可穿越边界条件,导致地面面元强度更大,地面效应更强,因此共轴双旋翼的拉力增益大于同实度的单旋翼.
|
图 13 共轴双旋翼与单旋翼的拉力系数及拉力增益 Figure 13 Thrust coefficient and gain of thrust of coaxial rotor and single rotor |
1) 地面效应使上、下旋翼尾迹向上卷起,下旋翼尾迹卷起高度大于上旋翼.由于低速流场气体的不可压缩性,共轴双旋翼尾迹在地面附近产生径向扩展.
2) 地面效应下的共轴双旋翼桨盘平面诱导速度由上、下旋翼和地面共同引起.随着旋翼高度的降低,地面对上下旋翼的上洗作用增大.同时,上、下旋翼的诱导速度分布更加均匀,旋翼的气动性能提高.
3) 随着旋翼高度的降低,共轴双旋翼的拉力逐渐增大且分布更均匀.在相同的悬停高度与功率下,共轴双旋翼受到的地面效应更强,其拉力系数及拉力增益均大于同实度的单旋翼.
| [1] |
王适存.
直升机空气动力学[M]. 北京: 航空专业教材编审组, 1985.
WANG Shicun. Aerodynamics of helicopter[M]. Beijing: Aviation Teaching Material Editor, 1985. |
| [2] |
DUWALT F A. Wakes of lifting propellers (rotors) in ground effect, CAL No.BB-16665-S-3[R]. : Cornell Aeronautical Laboratory, 1966.
|
| [3] |
孙茂, CURTISSH C. 近地低速飞行时旋翼尾涡系的畸变及其诱导速度[J].
空气动力学学报, 1989, 7(1): 35-42.
SUN Mao, CURTISS H C. Rotor vortex wake distortion and its induced velocity in ground effect at low speed[J]. Acta Aerodynamica Sinica, 1989, 7(1): 35-42. |
| [4] |
CURTISS HC, SUN M, PUTMAN W F, et al. Rotor aerodynamics in ground effect at low advance ratios[J].
Journal of the American Helicopter Society, 1984, 29(1): 48-55.
DOI: 10.4050/JAHS.29.48 |
| [5] |
LEE C S, HE C J.A free wake/ground vortex model for rotors at low speed in-ground-effect flight[C]//Proceedings of the 51st Annual Forum of the American Helicopter Society Forum.[S.L.]:[s.l.], 1995.
|
| [6] |
陈仁良, 辛冀, 李攀. 一种新的尾迹-地面干扰修正方法[J].
南京航空航天大学学报, 2012, 44(5): 694-699.
CHEN Renliang, XIN Ji, LI Pan. New rectification method for interaction of rotor wake vortices and ground[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2012, 44(5): 694-699. DOI: 10.16356/j.1005-2615.2012.05.017 |
| [7] |
辛冀, 李攀, 陈仁良. 地面效应中悬停旋翼的自由尾迹计算[J].
航空学报, 2012, 33(12): 2161-2170.
XIN Ji, LI Pan, CHEN Renliang. Free-wake analysis of hovering rotor in ground effect[J]. Acta Aeronautica et Astronutica Sinica, 2012, 33(12): 2161-2170. |
| [8] |
辛冀. 直升机旋翼地面效应研究[D]. 南京: 南京航空航天大学, 2014.
XIN Ji. Ground effect research for a helicopter rotor[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014. |
| [9] |
COLEMAN C P. A survey of theoretical and experimental coaxial rotor aerodynamic research, NASA TP 3675[R]. Washington DC: NASA, 1997.
|
| [10] |
叶靓, 徐国华. 共轴式双旋翼悬停流场和气动力的CFD计算[J].
空气动力学学报, 2012, 30(4): 437-442.
YE Liang, XU Guohua. Calculation on flow filed and aerodynamic force of coaxial rotors in hover with CFD method[J]. Acta Aerodynamic Sinica, 2012, 30(4): 437-442. DOI: 10.3969/j.issn.0258-1825.2012.04.003 |
| [11] |
朱正, 招启军, 李鹏. 悬停状态共轴刚性双旋翼非定常流动干扰机理[J].
航空学报, 2016, 37(2): 568-578.
ZHU Zheng, ZHAO Qijun, LI Peng. Unsteady flow interaction mechanism of coaxial rigid rotors in hover[J]. Acta Aeronautica et Astronutica Sinica, 2016, 37(2): 568-578. DOI: 10.7527/S1000-6893.2015.0106 |
| [12] |
KANG Ning, SUN Mao. Prediction of the flow field of a rotor in ground effect[J].
Journal of the American Helicopter Society, 1997, 42(2): 195-198.
DOI: 10.4050/JAHS.42.195 |
| [13] |
KANG Ning, SUN Mao. Simulated flowfields in near-ground operation of single-and twin-rotor configurations[J].
Journal of Aircraft, 2000, 37(2): 214-220.
DOI: 10.2514/2.2609 |
| [14] |
GRIFFITHS D A, LEISHMAN J G. A study of dual-rotor interference and ground effect using a free-vortex wake model[C]// Proceedings of the 58th Annual Forum of the American Helicopter Society. Montreal Canada:[s.l.], 2002.
|
| [15] |
覃燕华, 朱清华, 邵松. 共轴双旋翼悬停地面效应气动特性分析[J].
南京航空航天大学学报, 2015, 47(2): 266-274.
QIN Yanhua, ZHU Qinghua, SHAO Song. Aerodynamic characteristics analysis for hovering coaxial rotors in ground effect[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2015, 47(2): 266-274. DOI: 10.16356/j.1005-2615.2015.02.013 |
| [16] |
黄水林, 李春华, 徐国华. 基于自由尾迹和升力面方法的双旋翼悬停气动干扰计算[J].
空气动力学学报, 2007, 25(3): 390-395.
HUANG Shuilin, LI Chunhua, XU Guohua. An analytical method for aerodynamic interactions of twin rotors based upon free-vortex and lifting-surface models[J]. Acta Aerodynamica Sinica, 2007, 25(3): 390-395. DOI: 10.3969/j.issn.0258-1825.2007.03.021 |
| [17] |
GRIFFITHS D A, ANANTHAN S, LEISHMAN J G. Predictions of rotor performance in ground effect using a free-vortex wake model[J].
Journal of the American Helicopter Society, 2005, 50(4): 302-314.
DOI: 10.4050/1.3092867 |
| [18] |
辛冀, 李攀, 陈仁良. 基于三阶显式格式的旋翼时间步进自由尾迹计算与验证[J].
航空学报, 2013, 34(11): 2452-2463.
XIN Ji, LI Pan, CHEN Renliang. Prediction and validation of rotor time marching free wake based on 3rd order explicit numerical scheme[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(11): 2452-2463. DOI: 10.7527/S1000-6893.2013.0299 |
| [19] |
唐正飞, 李锋, 高正, 等. 用三维激光多谱勒测速仪对共轴双旋翼悬停流场的测定[J].
流体力学实验与测量, 1998, 12(1): 81-87.
TANG Zhengfei, LI Feng, GAO Zheng, et al. Measurement of the coaxial-rotor flow field in hovering using 3-D laser Doppler velocmeter[J]. Experiments and Measurements in Fluid Mechanics, 1998, 12(1): 81-87. |
| [20] |
LIGHT J S. Tip vortex geometry of a hovering helicopter rotor in ground effect[J].
Journal of American Helicopter Society, 1993, 38(2): 34-42.
DOI: 10.4050/JAHS.38.34 |
| [21] |
VALKOV T. Aerodynamic loads computation on coaxial hinge-less helicopter rotor, AIAA-90-0070[R].Reno: AIAA, 1990.
|
 2017, Vol. 49
2017, Vol. 49


