MEMS陀螺仪具有成本低、体积小、功耗低、抗冲击能力强等优点,近年来得到了快速的发展[1],然而由于存在较大的漂移,限制了它在很多领域的应用[2-3].所以,使用合适的去噪方法对MEMS陀螺仪的输出信号进行去噪处理,可以有效降低漂移的影响,从而提高精度[4].
MEMS陀螺仪通常采用的去噪方法包括卡尔曼滤波、时间序列分析、小波去噪等[5].小波在时频和细节描述的优越性拓展了它在MEMS陀螺去噪领域的应用[6].小波去噪方法可以分为:小波阈值法、模极大值法和平移不变量法等,而阈值法应用则比较多.这种方法的主要依据是:在小波域中,有用信号可以用较大的小波系数表示,噪声信号则相反,用较小的小波系数表示,那么通过设置一个合理的阈值,就可以将较小的小波系数滤除,保留较大的小波系数,从而实现对噪声信号的抑制[7].这种方法的难点就在阈值的选取上,由于阈值选择的固定性限制了小波方法的自适应性,所以小波去噪对多变信号的处理效果就较差[8].
为了克服小波阈值滤波的缺陷,稀疏分解去噪方法被提出并受到广泛关注.稀疏分解去噪主要原理是干净信号通过提升小波正变换后,得到的各个尺度下的小波系数都较小,也就是说小波系数是稀疏的;而当信号中含有噪声时,得到的小波系数中含有的较大幅值的小波系数就会变多,换言之,小波稀疏的稀疏性随之降低[9].所以,利用稀疏分解理论对非稀疏小波系数进行稀疏性恢复,可以达到去噪的目的.
恢复小波系数稀疏性过程中所采用的算法对于恢复后的系数的稀疏度有很大的影响,文献[10-14]采用贪婪算法中的正交匹配追踪算法(orthogonal matching pursuit, OMP),取得较好的效果.文献[15]采用凸松弛方法中的基追踪算法(basis pursuit, BP),也验证了稀疏分解去噪方法的优势.本文采用的梯度投影算法(gradient projection, GP)是凸松弛算法中的一种,相对于贪婪算法,此种算法具有全局最优解,而相对于基追踪算法运算效率更高.
1 MEMS陀螺仪数学模型低精度的MEMS陀螺仪输出模型可描述如下:
| $ W\left( t \right) = \omega \left( t \right) + {\omega _0}. $ |
式中:W(t)为输出信号, ω0为漂移,°/s.
MEMS陀螺仪的漂移通常包括:常值漂移、周期漂移和白噪声.由于MEMS陀螺仪性能较传统陀螺仪性能普遍不高,通常在连续工作时间较短的场合得到广泛应用,那么对其短时漂移特性的研究就显得更为重要,根据其短时漂移强周期性和规律性的特点,可以将其漂移的模型描述如下:
| $ {\omega _0} = {\varepsilon _b} + {\mathit{\Omega }_d}\sin \left( {2{\rm{ \mathsf{ π} }}{f_d} + {\theta _0}} \right) + n\left( t \right). $ |
式中:εb为陀螺仪的零偏,短时间内可以近似为一个常数;Ωd为周期分量的幅值;fd为周期分量的频率;θ0则为初始相位;n(t)为零均值高斯白噪声.
2 稀疏分解去噪与提升小波变换基本理论 2.1 稀疏分解去噪的数学模型本文先对一维信号进行研究,将信号和噪声的关系表示如下:
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{s}} + \mathit{\boldsymbol{n}}. $ |
式中:s为有用信号;n为高斯白噪声;y为带噪信号.y、s、n分别为一维实向量,且长度是M,假设n~N(0, σ2).
本文可以用下式来表示对y的稀疏分解
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{s}} + \mathit{\boldsymbol{n}} = \mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{n}}, $ | (1) |
假设n= Az,则式(1)可以表示为
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{s}} + \mathit{\boldsymbol{n}} = \mathit{\boldsymbol{A}}\left( {\mathit{\boldsymbol{x}} + \mathit{\boldsymbol{z}}} \right). $ |
值得注意的是,有用信号s在A上的分解系数x是稀疏的,或者说系数中的非零系数只有K个,而噪声信号n在A上的分解系数z是非稀疏的,而且非零的稀疏分布在整个域.本文要做的就是首先得到y在A上的分解系数,然后将其中幅值较大的K个系数选取出来,最后利用这K个系数所对应的原子的线性组合来近似本文需要的有用信号s.
假设n满足‖n‖2≤ε,本文可以将无噪情况下的稀疏分解的数学描述(P0)改写成带噪情况下的变体,如
| $ \left( {{P_{0,\delta }}} \right):\mathop {\min }\limits_\mathit{\boldsymbol{x}} {\left\| x \right\|_0}{\rm{s}}{\rm{.t}}{\rm{.}}{\left\| {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{Ax}}} \right\|_2} \le \delta . $ |
注意到,(P0, 0)≡(P0),进而,如果假设δ≥ε=‖y-s‖2时,式(P0, δ)问题存在稀疏解
| $ {\left\| {\mathit{\boldsymbol{\hat x}}} \right\|_0} = {\rm{spa}}\left( {{P_{0,\delta }}} \right) \le {\rm{spa}}\left( {{P_{0,\varepsilon }}} \right) \le {\left\| {{\mathit{\boldsymbol{x}}_0}} \right\|_o}, $ | (2) |
式中,spa(·)为问题的稀疏解.
从式(2)可以看出想要(P0, δ)满足条件很困难, 所以本文要解决这个问题,就需要寻求其他的表达方式,也就是基于l0范数的(P0, δ)问题的变体.
2.2 提升小波变换提升小波变换是基于提升方案的小波变换.由于提升小波只在时域上进行分析,而且它的反变换具有简单直接和高效等优点,所以本文采用这种变换方式.正向变换的过程包括分解、预测和更新.反向变换则相反,正向变换和反向变换的步骤如图 1所示.
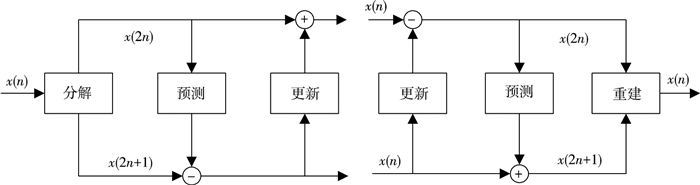
|
图 1 提升小波变换分解与重建 Figure 1 Lifting wavelet transform decomposition and reconstruction |
本文采取的是5/3提升小波变换,其中正反变换的公式如下:
| $ \begin{array}{*{20}{c}} {\left\{ \begin{array}{l} \mathit{\boldsymbol{x}}\left( {2n} \right) = \mathit{\boldsymbol{c}}\left( n \right) - \left[ {\frac{{\mathit{\boldsymbol{d}}\left( {2n} \right) + \mathit{\boldsymbol{d}}\left( {2n + 2} \right) + 2}}{4}} \right],\\ \mathit{\boldsymbol{x}}\left( {2n + 1} \right) = \mathit{\boldsymbol{d}}\left( n \right) - \left[ {\frac{{\mathit{\boldsymbol{x}}\left( {2n} \right) + \mathit{\boldsymbol{x}}\left( {2n + 2} \right) + 2}}{2}} \right]; \end{array} \right.}\\ {\left\{ \begin{array}{l} \mathit{\boldsymbol{d}}\left( n \right) = \mathit{\boldsymbol{x}}\left( {2n + 1} \right) - \left[ {\frac{{\mathit{\boldsymbol{x}}\left( {2n} \right) + \mathit{\boldsymbol{x}}\left( {2n + 2} \right)}}{2}} \right],\\ \mathit{\boldsymbol{c}}\left( n \right) = \mathit{\boldsymbol{x}}\left( {2n} \right) + \left[ {\frac{{\mathit{\boldsymbol{d}}\left( n \right) + \mathit{\boldsymbol{d}}\left( {n - 1} \right) + 2}}{4}} \right]. \end{array} \right.} \end{array} $ |
对于稀疏分解去噪与提升小波变换基本理论所述的(P0, δ)问题,考虑凸优化方法,用l1范数代替l0范数,即有
| $ \left( {{P_{1,\delta }}} \right):\mathop {\min }\limits_x {\left\| x \right\|_1}{\rm{s}}{\rm{.t}}{\rm{.}}{\left\| {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{Ax}}} \right\|_2} \le \delta , $ | (3) |
求解(P1, δ)问题,可以将其与基追踪去噪(basis pursuit denoising, BPDN)算法关联起来,并修改式(3)如下
| $ \left( {{{P'}_{1,\lambda }}} \right):\mathop {\min }\limits_x {\left\| \mathit{\boldsymbol{x}} \right\|_1} + \left\| {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{Ax}}} \right\|_2^2/\lambda , $ |
此式是一个拉格朗日优化问题,令参数λ=λ(y, δ),则(P1, δ)与(P′1, λ(y, δ))的解相同.由于该问题采用一般方法计算量非常大,所以本文引入梯度投影思想来简化计算,提高运算效率.
首先,(P1, δ)问题可得变式如下:
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_x \frac{1}{2}\left\| {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{Ax}}} \right\|_2^2 + \tau {{\left\| x \right\|}_1},}\\ {x \in {R^n},y \in {R^k}.} \end{array} $ | (4) |
式中,A为一个k×n矩阵,而τ为非负参数,y= Ax+n.
为求解此问题,通过引入向量u, v对x做如下替换:
| $ \mathit{\boldsymbol{x}} = \mathit{\boldsymbol{u}} - \mathit{\boldsymbol{v}},\mathit{\boldsymbol{u}} \ge 0,\mathit{\boldsymbol{v}} \ge 0. $ |
式中,ui=(xi)+, vi=(-xi)+, i=1, 2, …, n,(·)+表示正部运算符,(x)+=max{0, x},由此,本文可得
那么,问题(4)可被转换成一个带约束的二次线性规划问题如下:
| $ \begin{array}{l} \mathop {\min }\limits_{u,v} \frac{1}{2}\left\| {y - \mathit{\boldsymbol{A}}\left( {\mathit{\boldsymbol{u}} - \mathit{\boldsymbol{v}}} \right)} \right\|_2^2 + \tau {\bf{1}}_n^T\mathit{\boldsymbol{u}} + \tau {\bf{1}}_n^T\mathit{\boldsymbol{v}},\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\mathit{\boldsymbol{u}} \ge 0,\\ \;\;\;\;\;\mathit{\boldsymbol{v}} \ge 0. \end{array} $ | (5) |
问题(5)又可以写成如下的标准形式:
| $ \begin{array}{l} \mathop {\min }\limits_z {c^{\rm{T}}}\mathit{\boldsymbol{z}} + \frac{1}{2}{\mathit{\boldsymbol{z}}^{\rm{T}}}\mathit{\boldsymbol{Bz}} \equiv F\left( \mathit{\boldsymbol{z}} \right),\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\mathit{\boldsymbol{z}} \ge 0. \end{array} $ | (6) |
其中:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{z}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{u}}\\ \mathit{\boldsymbol{v}} \end{array}} \right],\mathit{\boldsymbol{b = }}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{y}},\mathit{\boldsymbol{c}} = \tau {{\bf{1}}_{2n}} + \left[ \begin{array}{l} - \mathit{\boldsymbol{b}}\\ \mathit{\boldsymbol{b}} \end{array} \right],}\\ {\mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}}&{ - {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}}\\ { - {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}}&{{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \end{array}} \right].} \end{array} $ | (7) |
表面看来,转化后的问题维数是问题(4)的2倍,而实际上这种维数上的增大对于问题求解影响很小.由式(7)可以得到
| $ \mathit{\boldsymbol{Bz}} = \mathit{\boldsymbol{B}}\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{u}}\\ \mathit{\boldsymbol{v}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}\left( {\mathit{\boldsymbol{u}} - \mathit{\boldsymbol{v}}} \right)}\\ { - {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}\left( {\mathit{\boldsymbol{u}} - \mathit{\boldsymbol{v}}} \right)} \end{array}} \right], $ | (8) |
那么本文要计算Bz只需要计算向量u-v和ATA.
由式(6)得其投影为
| $ \nabla F\left( \mathit{\boldsymbol{z}} \right) = c + \mathit{\boldsymbol{Bz}}, $ |
那么,▽F(z)的计算只需要A和AT的乘法运算(假设c在算法之前已经计算).
亦可由式(8)得zTBz如下
| $ {\mathit{\boldsymbol{z}}^{\rm{T}}}\mathit{\boldsymbol{Bz}} = {\left( {\mathit{\boldsymbol{u}} - \mathit{\boldsymbol{v}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}\left( {\mathit{\boldsymbol{u}} - \mathit{\boldsymbol{v}}} \right) = \left\| {\mathit{\boldsymbol{A}}\left( {\mathit{\boldsymbol{u}} - \mathit{\boldsymbol{v}}} \right)} \right\|_2^2, $ |
由于
本文将描述使用GP算法求解该问题具体步骤:
在GP算法中通过迭代来确定k.
首先,选择标量参数α(k) > 0,并令
| $ {\mathit{\boldsymbol{w}}^{\left( k \right)}} = {\left( {{\mathit{\boldsymbol{z}}^{\left( k \right)}} - {\alpha ^{\left( k \right)}}\nabla F\left( {{\mathit{\boldsymbol{z}}^{\left( k \right)}}} \right)} \right)_ + }. $ |
然后,选择参数λ(k)∈[0, 1],令
| $ {\mathit{\boldsymbol{z}}^{\left( {k + 1} \right)}} = {\mathit{\boldsymbol{z}}^{\left( k \right)}} + {\lambda ^{\left( k \right)}}\left( {{\mathit{\boldsymbol{w}}^{\left( k \right)}} - {\mathit{\boldsymbol{z}}^{\left( k \right)}}} \right). $ |
再定义向量g(k)如下:
| $ {\mathit{\boldsymbol{g}}^{\left( k \right)}} = \left\{ \begin{array}{l} {\left( {\nabla F\left( {{\mathit{\boldsymbol{z}}^{\left( k \right)}}} \right)} \right)_i},\mathit{\boldsymbol{z}}_i^{\left( k \right)} > 0\;{\rm{or}}\;{\left( {\nabla F\left( {{\mathit{\boldsymbol{z}}^{\left( k \right)}}} \right)} \right)_i} < 0;\\ 0,\;{\rm{otherwise}}. \end{array} \right. $ |
并选择α0的初始值为
| $ {\alpha _0} = \mathop {\arg \min }\limits_\alpha F\left( {{\mathit{\boldsymbol{z}}^{\left( k \right)}} - \alpha {\mathit{\boldsymbol{g}}^{\left( k \right)}}} \right). $ |
具体计算过程如下:
| $ {\alpha _0} = \frac{{{{\left( {{\mathit{\boldsymbol{g}}^{\left( k \right)}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{g}}^{\left( k \right)}}}}{{{{\left( {{\mathit{\boldsymbol{g}}^{\left( k \right)}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{g}}^{\left( k \right)}}}}. $ | (9) |
那么,GP算法解决此问题的具体过程如下.
Step 1(初始化) 给定z0,选择参数β∈(0, 1)和μ∈(0, 1 2),并设定k=0.
Step 2 通过式(9)计算α0,并用mid(αmin, α0, αmax)替换α0.其中[αmin, αmax]是本文为了防止α0的值过大或过小而定义的一个区间,0 < αmin < α0 < αmax,而mid(αmin, α0, αmax)则是α0, αmin, αmax3个元素的中间值.
Step 3(回溯行搜索法) 选择αk作为序列α0, βα0, β2α0, …的第1个数,那么就有
| $ \begin{array}{l} F\left. {\left( {{{\left( {{\mathit{\boldsymbol{z}}^{\left( k \right)}} - {\alpha ^{\left( k \right)}}\nabla F\left( {{\mathit{\boldsymbol{z}}^{\left( k \right)}}} \right)} \right)}_ + }} \right)} \right) \le \\ F\left( {{\mathit{\boldsymbol{z}}^{\left( k \right)}}} \right) - \mu \nabla F{\left( {{\mathit{\boldsymbol{z}}^{\left( k \right)}}} \right)^{\rm{T}}}\left. {{{\left( {{\mathit{\boldsymbol{z}}^{\left( k \right)}} - {\alpha ^{\left( k \right)}}\nabla F\left( {{\mathit{\boldsymbol{z}}^{\left( k \right)}}} \right)} \right)}_ + }} \right), \end{array} $ |
并令z(k+1)=(z(k)-α(k)▽F(z(k)))+.
Step 4 进行收敛性测试,如果满足那么就在z(k+1)处终止算法,否则令k←k+1,并回到Step 2.
基于上述分析,可以得出利用稀疏分解和提升小波变换求解此问题的算法流程如图 2所示.
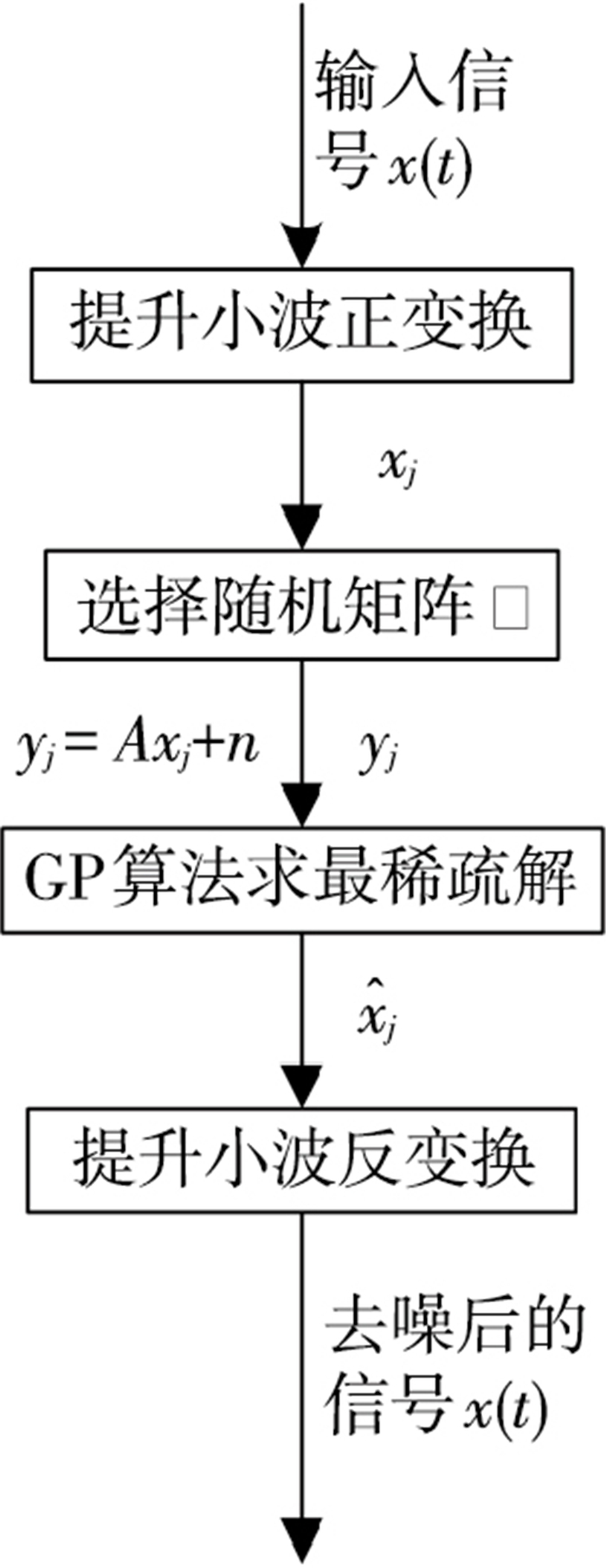
|
图 2 算法流程 Figure 2 Algorithm flow chart |
将MEMS陀螺仪ADXRS300放置于安装在隔离地基的温控转台上,使用PC104工控机对输出数据进行采集处理.
待陀螺仪工作一段时间,输出稳定后,以200 Hz的采样频率采集一组MEMS陀螺仪ADXRS300的静态数据,作为陀螺仪随机漂移的时间序列.取该时间序列中长度为3 600的一段序列作为实验数据.然后分别采用本文方法和小波软阈值滤波方法对陀螺仪输出信号进行处理,然后比较两种方法的去噪效果.本文采用了db4作为小波基,对输出信号进行3尺度分解,小波软阈值滤波方法选用了“Birge Massart”阈值.
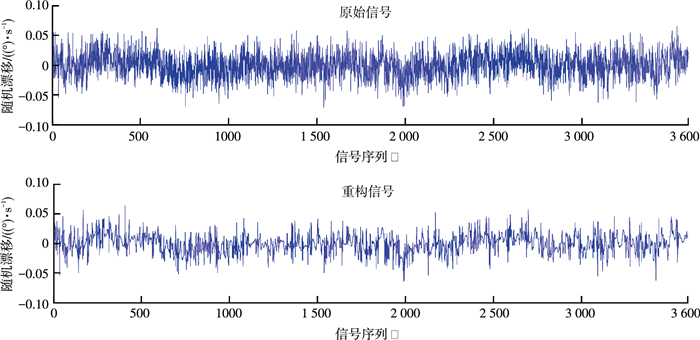
|
图 3 小波滤波去噪效果 Figure 3 Denosing effect with wavelet threshold de-nosing |
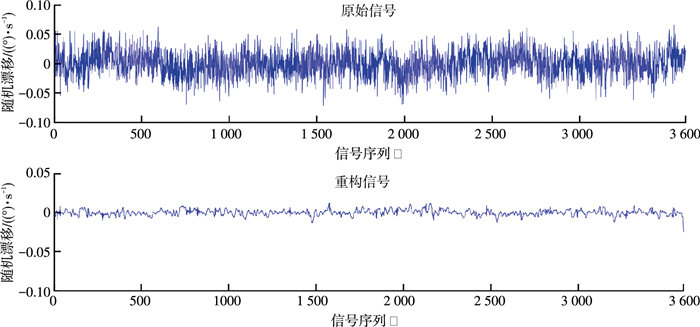
|
图 4 本文方法去噪效果 Figure 4 Denosing effect with new method |
从图 3、4可以看出,相对于小波阈值去噪方法,使用本文方法处理后的信号幅值下降更明显.另外,利用本文方法进行处理后的信号毛刺更少,也就是说处理后信号的零偏稳定性更好.
为更好的验证本文所提出去噪方法在MEMS陀螺信号处理中的可行性,设计了相应的跑车试验,具体试验条件描述如下:将MEMS陀螺仪ADXRS300固定放置在车载平台上,并使用PC104工控机对输出信号进行实时采集.实验的流程为先150 s预热,然后200 s的跑车,跑车路段包括直线和弯道,且不保持匀速行驶.
选择一组实地跑车实验中的MEMS陀螺仪数据,分别使用本文方法和小波阈值去噪方法对其进行分析处理.为了定量分析此两种方法的性能,选择均方差和信噪比两项指标来衡量其去噪效果.由均方差和信噪比的定义可知,同一信号去噪处理后,均方差越小,信噪比越大则去噪效果越好.
| $ {\rm{MSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = q}^N {{{\left( {x\left( i \right) - \hat x\left( i \right)} \right)}^2}} } , $ |
| $ {\rm{SNR}} = 10\lg \left[ {\sum\limits_{i = 1}^N {{{\left( {x\left( i \right)} \right)}^2}} /\sum\limits_{i = 1}^N {{{\left( {x\left( i \right) - \hat x\left( i \right)} \right)}^2}} } \right]. $ |
处理结果见表 1.
| 表 1 去噪处理结果 Table 1 Results of the signal processed |
从表 1中可以看出,本文方法处理后的MEMS陀螺输出信号,无论是信噪比还是均方差都优于小波阈值去噪法.
图 5是本文所使用的梯度投影算法与基追踪算法及l1_ls算法在解决此类问题时性能的对比图.由图 5可以看出梯度投影算法更稳定,且达到收敛所需迭代次数更少.
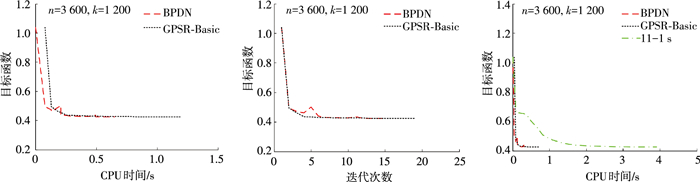
|
图 5 不同算法计算效率对比 Figure 5 Comparison of computational efficiency with different algorithm |
由于OMP并不是和GP同类型的凸松弛方法,不是带约束的线性规划问题,也就不存在目标函数,所以不能以目标函数收敛所需时间和迭代次数作为指标和GP对比.所以为充分对比这两种算法的性能如何,分别使用这两种算法稀疏重建一组信号x,x是在长度为n的全零信号中随机插入m个非零值得到的仿真信号.y= Ax + N为观测信号,N为白噪声.
图 6分别是用这两种方法对信号进行处理并达到相同稀疏度后重构信号的MSE和CPU时间的对比图.
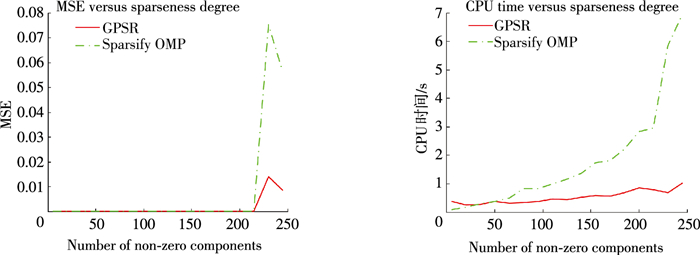
|
图 6 GP与OMP性能对比 Figure 6 Comparison of average MSE and CPU time for GP and OMP |
从图 6中可以看出:当信号x的稀疏度比较小(x中的非零元素个数m > 220)时,采用GP算法处理后的信号的MSE更小,而且很明显GP的速度比OMP要快(除了m < 50这种极端的情况).
而在分别使用这两种方法对本文实测静态数据进行处理时,所需要的CPU时间分别为:tGPSR=1.248 0 s,tOMP=12.214 9 s,可见GP方法还是明显要快于OMP算法.
5 结论1) 本文将稀疏分解与提升小波变换相结合,并采用梯度投影算法恢复信号的稀疏性,进而提出了基于梯度投影的改进稀疏分解去噪算法,并用于MEMS陀螺信号的处理.
2) 本文算法与小波软阈值滤波方法对比结果表明,本文算法在动静态条件下都可以有效地去除MEMS陀螺仪输出信号中的噪声,尤其是在静态条件下的去噪效果要明显优于小波阈值滤波方法.
3) 本文采用的梯度投影算法与正交匹配追踪算法和基追踪算法的对比结果表明,梯度投影算法具有更高的运算效率,适合在线滤波,同时具有良好的稳定性和全局优化能力.
| [1] |
BARBOURN, CONNELLY J, GILMORE J, et al. Micromechanical silicon instrument and system development at draper laboratory [C]//AIAA Guidance Navigation and Control Conference. San Diego: AIAA, 1996: 1-7.DOI: 10.2514/6.1996-3709.
|
| [2] |
王昊, 王俊璞, 田蔚风, 等. 梯度RBF神经网络在MEMS陀螺仪随机漂移建模中的应用[J].
中国惯性技术学报, 2006, 14(4): 44-48.
WANG Hao, WANG Junpu, TIAN Weifeng, et al. Application of gradient radial basis function network in the modeling of MEMS gyro's random drift[J]. Journal of Chinese Intertial Technology, 2006, 14(4): 44-48. DOI: 10.13695/j.cnki.12-1222/o3.2006.04.010 |
| [3] |
王新龙, 李娜. MEMS陀螺仪随机误差的建模与分析[J].
北京航空航天大学学报, 2012, 38(2): 170-174.
WANG Xinlong, LI Na. Error modeling and analysis for random drift of MEMS gyroscope[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(2): 170-174. DOI: 10.13700/j.bh.1001-5965.2012.02.020 |
| [4] |
李泽民, 段凤阳, 马佳智. 基于支持向量机的MEMS陀螺仪随机漂移补偿[J].
传感技术学报, 2012, 25(8): 1084-1087.
LI Zemin, DUAN Fengyang, MA Jiazhi. Random drift compensation of MEMS gyroscope based on support vector machine[J]. Chinese Journal of Sensors and Actuators, 2012, 25(8): 1084-1087. DOI: 10.3969/j.issn.1004-1699.2012.08.013 |
| [5] |
于湘涛, 张兰. 基于小波最小二乘支持向量机的加速度计温度建模和补偿[J].
中国惯性技术学报, 2011, 19(1): 95-98.
YU Xiangtao, ZHANG Lan. Temperature modeling and compensation of accelerometer based on least squares wavelet support vector machine[J]. Journal of Chinese Inertial Technology, 2011, 19(1): 95-98. DOI: 10.13695/j.cnki.12-1222/o3.2011.01.014 |
| [6] |
秦伟伟, 郑志强, 刘刚, 等. 基于小波分析与LSSVM的陀螺仪随机漂移建模[J].
中国惯性技术学报, 2008, 16(6): 721-724, 729.
QIN Weiwei, ZHENG Zhiqiang, LIU Gang, et al. Modeling method of gyroscope's random drift based on wavelet analysis and LSSVM[J]. Journal of Chinese Inertial Technology, 2008, 16(6): 721-724, 729. DOI: 10.13695/j.cnki.12-1222/o3.2008.06.013 |
| [7] |
石光明, 刘丹华, 高大化, 等. 压缩感知理论及其研究进展[J].
电子学报, 2009, 37(5): 1070-1081.
SHI Guangming, LIU Danhua, GAO Dahua, et al. Advances in theory and application of compressed sensing[J]. Acta Electronica Sinica, 2009, 37(5): 1070-1081. DOI: 10.3321/j.issn:0372-2112.2009.05.028 |
| [8] |
TSAIG Y, DONOHO D L. Extensions of compressed sensing[J].
Signal Processing, 2006, 86(3): 549-571.
DOI: 10.1016/j.sigpro.2005.05.029 |
| [9] |
FIGUEIREDO M A T, NOWAK R D, WRIGHT S J. Gradient projection for sparse reconstruction: application to compressed sensing and other inverse problems[J].
IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4): 586-594.
DOI: 10.1109/JSTSP.2007.910281 |
| [10] |
程承, 潘泉, 王申龙, 等. 基于压缩感知理论的MEMS陀螺仪信号降噪研究[J].
仪器仪表学报, 2012, 33(4): 769-773.
CHENG Cheng, PAN Quan, WANG Shenlong, et al. Research on MEMS gyroscope signal denoising based compressed sensing theory[J]. Chinese Journal of Scientific Instrument, 2012, 33(4): 769-773. DOI: 10.3969/j.issn.0254-3087.2012.04.008 |
| [11] |
张海鹏, 房建成. MEMS陀螺仪短时漂移特性实验研究[J].
中国惯性技术学报, 2007, 15(1): 100-104.
ZHANG Haipeng, FANG Jiancheng. Short-time drift characteristic of MEMS Gyroscope[J]. Journal of Chinese Inertial Technology, 2007, 15(1): 100-104. DOI: 10.3969/j.issn.1005-6734.2007.01.026 |
| [12] |
DAI Wei, MILENKOVIC O. Subspace pursuit for compressive sensing signal reconstruction[J].
IEEE Transactions on Information Theory, 2009, 55(5): 2230-2249.
DOI: 10.1109/TIT.2009.2016006 |
| [13] |
LIVSHITZ E.
On efficiency of orthogonal matching pursuit[M]. [S.L.]: Preprint, 2010.
|
| [14] |
MALLAT S G, ZHANG Zhifeng. Matching pursuits with time-frequency dictionaries[J].
IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415.
DOI: 10.1109/78.258082 |
| [15] |
ZHU Wenjie, WANG Guanglong, QIAO Zhongtao, et al. A novel noise reduction algorithm of mems gyroscope based on compressive sensing and lifting wavelet transform[J].
Key Engineering Materials, 2014, 609-610: 1138-1143.
DOI: 10.4028/www.scientific.net/KEM.609-610.1138 |
 2017, Vol. 49
2017, Vol. 49


