利用天文图像对外太空进行研究是深空探索的一个重要分支.从获得的天文图像可以直接得知某一星体上的地表结构, 是否存在未知生命等重要信息.为了能够获得更多的天文信息, 天文图像的采集一般都是采用高分辨率CMOS/CCD传感器, 但是卫星或者其他的深空探测设备所携带的存储空间有限，存储这些高分辨率图像将会给有限的存储空间带来较大压力.为解决这一难题, 天文图像在存储之前通常都要经过压缩处理.然而常用的JPEG/JPEG-2000方法^[1-3]很难获得较低的图像压缩采样比.

另一方面, 由于环境、拍摄条件等因素的影响, 天文图像在采集和传输的过程中经常受到噪声信号的干扰, 在地面接收站接收到的天文图像通常含有噪声.从接收到的图像中很难分辨出某一区域的实际地形特征.因此在接收到这些天文图像后, 通常要进行去噪处理.然而目前大部分的去噪方法经常由于很难从高维数的信号观测值中获得足够有效的图像信息, 导致重构信号的质量较差^[4-5].为有效解决高维数信号的重建问题, 学者们一直在探索如何从高维数信号中获得一种低维的信号结构, 同时保证原始信号能从这种低维结构中获得精确重建.即, 从信号中提取重要的信息同时舍弃非重要信息, 直接使用这些重要信息重建高维数信号.近几年提出的信号稀疏性^[5-6]可能是探索信号低维结构的一种比较简单方法.

基于信号的稀疏性，Donoho^[7]提出了著名的压缩感知(compressed sensing, CS)理论.该理论一经提出, 就引起了各领域的极大关注.它指出:如果信号在某一稀疏变换基上是稀疏的, 则可以使用一个与该稀疏基不相关的低维测量矩阵对原信号进行观测, 同时使用某一CS重建算法就可以从获得的少量信号观测值中精确重构原始信号.可以看出, 信号在采集的同时就已经完成了压缩过程.传统的奈奎斯特/香农采样定理要求信号的采样速率必须大于或者等于两倍的信号带宽才能够精确重建原始信号, 但是采样速率在低于两倍的信号带宽时, CS方法仍可以精确重建原始信号.因此, CS理论可以有效地解决高维数信号的重建问题, 本文将其应用到高分辨率天文图像去噪中.

CS理论主要包含3个部分:稀疏变换、测量矩阵和重建算法.本文主要关注于如何设计一个高性能的重建算法.经过近几年的努力, 学者们提出了许多的重建算法, 例如线性规划类算法^[8-9]、迭代收缩阈值类(iterative shrinkage thresholding, IST)算法^[10-12]、梯度下降类方法^[13]和贝叶斯类方法^[14]等.在这些算法当中, IST算法设计简单且易于实现, 更重要的是大部分的稀疏基都能较容易地应用到IST框架当中.这些优势使得IST算法经常受到学者们的青睐.然而该算法的收敛速度较慢, 去噪性能也需要进一步提高.

为了提高梯度下降法的收敛速度, Barzilai等^[15]提出了著名的BB线性搜索步长, 并取得较快的收敛效果.本文将其应用到IST算法中调节其收敛速度.在图像去噪中, 通常采用阈值去噪方法对图像信息进行筛选, 本文提出一种下降VisuShrink收缩阈值筛选天文图像信息.阈值去噪虽然设计简单且能获得较好的去噪效果, 但在奇异点(如边缘或者纹理)附近会出现较大的幅值振荡, 最终导致重构的图像出现伪吉布斯现象^[16].循环平移方法^[17-18]可有效地减小或者消除这种幅值振荡, 提高重构图像质量.本文将其应用到IST算法中, 在迭代过程中对重构的天文图像进行调整.基于上述技术, 本文提出了高性能的IST改进算法.实验结果表明, 该算法可以以较快的收敛速度重构一幅清晰的天文图像.当压缩采样比较低时, 该算法也具有较好的重建性能.

1 压缩感知去噪模型

假设某一N×1信号x是K-稀疏的^[6-7], 则可以用一个低维非自适应矩阵(又称为测量矩阵) Ф ∈ R^M×N(M≪N)对原始信号x进行观测, 进而得到低维含噪观测值y, 可表示为

$ y = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}x + e. $

(1)

从式(1)可以看出, 由于M≪N, 从y中重构出原始信号x是一个病态问题.然而, CS理论指出如果信号x在某个正交基Ψ上是稀疏的, 同时测量矩阵Ф满足RIP准则, 则原始信号x可以获得高概率重构^{[3-5, 13, 19]}.这里可以通过求解线性规划的最优解问题重建原始信号.此时, 式(1)可以改写为

$ y = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}x + e = {\varPhi}\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}^{-1}}x + e = \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}s + e, $

(2)

式中s= Ψ^-1x为稀疏系数.这里Θ = ΦΨ可以作为CS测量矩阵直接对s进行观测.测量矩阵Ф要求与稀疏基Ψ不相关, 两者越不相关, 需要的测量次数就越少, 则可以获得更低的信号压缩采样比.

具有稀疏限制的l₁范数最小化方法经常用来求解CS问题(2), 即

$ \mathop {{\rm{min}}}\limits_x \left\{ {\frac{1}{2}\left\| {y-\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}x} \right\|_{_2}^{^2} + \mathit{\boldsymbol{\lambda }}{{\left\| {{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}^{-1}}x} \right\|}_{{l_1}}}} \right\}, $

或者转化为对稀疏系数s的求解, 可表示为

$ \mathop {{\rm{min}}}\limits_s \left\{ {\frac{1}{2}\left\| {y-\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}s} \right\|_{_2}^{^2} + \mathit{\boldsymbol{\lambda }}{{\left\| s \right\|}_{{l_1}}}} \right\}, $

式中第1项代表惩罚项, 用来估算计算值与观测值之间的偏差；第2项为正则化项, 表示原始信号的先验知识.

2 高性能IST算法

经典的IST算法迭代过程可描述为

$ {x_{k + 1}} = {x_k} + {H_S}({\mu _k}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\left( {y-\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{x_k}} \right)). $

式中：μ_k为线性搜索步长, 为了计算方便通常设定为1, 虽然简化了计算, 但影响了算法的收敛速度；H_S(·)表示阈值算子, 通常考虑为硬阈值算子.其中

$ {H_S}\left( x \right) = \left\{ \begin{array}{l} x, \left| x \right| \ge T;\\ 0, \left| x \right| < T. \end{array} \right. $

式中T为阈值, 本文考虑为VisuShrink阈值(通用阈值) $ \sigma \sqrt {2\log \left( {N \times N} \right)} $, 其中σ为噪声标准差.如果重构一幅N×N高维数图像, 阈值T会随着N×N的增大而变得过大, 在迭代过程中导致较多的细节特征信息丢失.本文提出了一种下降VisuShrink收缩阈值在迭代过程中对图像信息进行筛选, 可表示为

$ T = \left( {1-\frac{q}{Q}} \right)\sigma \sqrt {2{\rm{log}}\left( {N \times N} \right)} . $

式中：q为迭代索引；Q为最大迭代次数.当q=0时, T为通用阈值.

2.1 BB线性搜索步长

最速下降法^[20]的迭代过程可表示为

$ {x_{k + 1}} = {x_k}-{\mu _k}{f_k}. $

(3)

式中：f_k=f(x_k)为任一目标函数Γ在位置x_k处的梯度向量；μ_k>0为线性搜索步长, 它要求满足以下条件：

$ \mathit{\Gamma} \left( {{x_k}-{\mu _k}} \right) = \mathop {{\rm{min}}}\limits_\mu \mathit{\Gamma} \left( {{x_k}-\mu {f_k}} \right). $

令目标函数$\mathit{\Gamma} = \frac{1}{2}\left\| {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}x-y} \right\|_2^2 $, 可以得到以下关系式

$ {f_k} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{x_k}-f} \right), $

和经典的SD迭代步长算子为

$ {\mu _k} = \frac{{\left\| {{f_k}} \right\|_{_2}^{^2}}}{{f_{_k}^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{f_k}}}. $

为了获得高性能的步长算子, 文献[15]用前一次的迭代信息设定当前迭代所使用的步长算子, 同时修改了式(3)的迭代过程, 即

$ {x_{k + 1}} = {x_k}-{D_k}{f_k}, $

式中D_k=μ_kI.其中I为单位向量.为了保证它具有某种拟牛顿特性, 需要满足以下任一限制条件：

$ \begin{array}{l} \min {\left\| {{s_{k-1}}-{D_k}{{f'}_{k-1}}} \right\|_2}, \\ {\rm{min}}\left\| {D_{_k}^{^{ - 1}}{s_{k - 1}} - {{f'}_{k - 1}}} \right\|. \end{array} $

式中：s_k－1=x_k－x_k－1, f′_k－1=f_k－f_k－1.基于上述条件，文献[15]提出了著名的BB步长算子, 可表示为:

$ \begin{array}{l} \mu _k^{{\rm{BB1}}} = \frac{{s_{K-1}^{\rm{T}}{{f'}_{k-1}}}}{{\left\| {{{f'}_{k-1}}} \right\|_2^2}}, \\ \mu _k^{{\rm{BB2}}} = \frac{{\left\| {{s_{k - 1}}} \right\|_2^2}}{{s_{K - 1}^{\rm{T}}{{f'}_{k - 1}}}}. \end{array} $

文献[20]证明了BB步长算子比SD步长算子更能有效地提升最速下降法的收敛速度.本文将BB步长算子应用到IST算法中调节其收敛速度.

2.2 循环平移方法

在图像去噪的过程中, 当一幅图像包含有较多奇异点时, 将会遇到如下问题:对于某一个奇异点具有较好去噪效果的平移量可能对另一个奇异点去噪效果较差.因此, 对于包含较多纹理和边缘特征的天文图像, 就很难获得针对所有奇异点都具有较好去噪效果的最佳平移量.循环平移方法可有效解决这一难题, 其循环平移过程可描述为

$ \tilde x = \frac{1}{{{K_1}{K_2}}}\sum\limits_{i, j = 1}^{{K_1}, {K_2}} {{C_{- i, - j}}} \left( {{S^{- 1}}\left( {\theta \left[{S\left( {{C_{i, j}}\left( x \right)} \right)} \right]} \right)} \right), $

式中K₁、K₂分别为沿行和列方向的最大平移量.在小波变换中，如果测试一幅N×N图像x且N=2^K, 则认为K₁=K₂=K为最大平移量.C_{i, j}(x)为定义的循环平移算子，对于二维图像x(m, n), 可定义为

$ {C_{i, j}}\left( x \right) = x\left[{\bmod \left( {m + i} \right)/N, \bmod \left( {n + j} \right)/N} \right]. $

C_{-i, -j}(x)为C_{i, j}(x)的逆过程, 可表示为

$ {C_{- i, - j}}\left( x \right) = {\left[{{C_{i, j}}\left( x \right)} \right]^{ -1}}. $

此外，S(x)为小波变换过程, S^-1(x)为小波逆变换.θ(x)为阈值函数, 本文将其考虑为硬阈值函数H_S(x), 并且阈值T为下降VisuShrink收缩阈值.

2.3 本文算法

综上所述, 本文算法的设计步骤概括如下：

1) 初始化过程.初始化迭代索引q=0, 最大迭代次数Q=30和重构图像x_q=0.

2) 计算下降VisuShrink收缩阈值和BB步长算子μ_q.

3) 使用下式更新估计值.

$ {x_{q + 1}} = {x_q} + {H_S}\left( {{\mu _q}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\left( {y-\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{x_q}} \right)} \right). $

4) 对重构的图像进行循环平移, 可表示为

$ {{\tilde x}_{q + 1}} = \frac{1}{{{K_1}{K_2}}}\sum\limits_{i, j = 1}^{{K_1}, {K_2}} {{C_{- i, - j}}} \left( {{S^{- 1}}\left( {{H_S}\left[{{C_{i, j}}\left( {{x_{q + 1}}} \right)} \right]} \right)} \right). $

5) $ {x_{q + 1}} = {{\tilde x}_{q + 1}} $.

6) q=q+1.如果q=Q, 输出重构图像; 否则, 进入步骤2).

3 实验及分析

本文考虑引入的噪声信号为高斯白噪声, 同时为了验证本文算法的去噪性能, 将它与传统IST算法、基于全变差方法的IST算法(IST-TV)^[3]以及基于循环平移方法的IST算法(IST-CS)对比.本文的压缩采样比定义为:观测值数量/信号长度.首先测试大小为1 024×1 024的月球图像, 并设定压缩采样比为0.3和噪声标准差${\hat \sigma } $ =10.图 1显示了不同重构算法重构得到的结果.

从图 1可以看出, 与其他算法相比, 本文算法能获得较好的视觉质量和较高的峰值信噪比(PSNR), 但花费的重构时间(reconstruction time, RT)较长.同时可以看出, IST-TV、IST-CS和本文算法都能有效地抑制伪吉布斯效应.

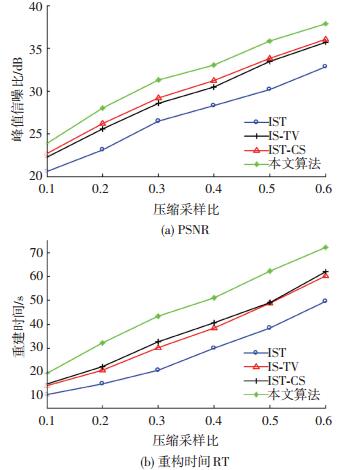
设定$ {\hat \sigma } $=10，图 2(a)、(b)分别显示了PSNR和RT随压缩采样比增长的变化曲线.可以看出, 随着压缩采样比的增长, 不同算法的重构能力逐渐提高.与其他算法相比, 本文算法仍能获得较高的PSNR值, 但花费的重构时间也相对较长.

设定噪声标准差和压缩采样比不变, 如图 3所示不同算法随迭代次数增长获得的PSNR值.可以看出, 本文算法具有比其他算法更快的收敛速度.

测试另一幅天文图像(木星图像), 设定压缩采样比为0.1和$ {\hat \sigma } $=10.图 4显示了不同算法重构得到的结果.可以看出, 当压缩采样比较低时, 本文算法仍可获得相对较好的视觉质量和较高的PSNR.

测试更多的天文图像, 表 1显示了当$ {\hat \sigma } $=10, 不同算法随压缩采样比变化时获得的PSNR值；表 2显示了当压缩采样比为0.3时, 不同算法随$ {\hat \sigma } $的增加获得的PSNR值.从表 1、2可以看出, 针对不同的天文图像, 本文算法仍具有较好的重建性能.

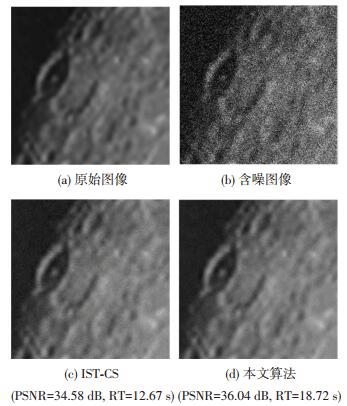
测试本文算法对天文图像特征的重构能力, 从原始月球图像中选取大小为512×512的局部特征图像作为实验图像.设定压缩采样比为0.3和$ {\hat \sigma } $=10, 图 5显示了不同算法重构得到的结果.可以看出, 与IST-CS算法相比, 本文算法能恢复较多的细节特征.

4 结论

1) 本文将压缩感知理论应用到天文图像去噪, 并在迭代收缩阈值算法的基础上, 提出了一种高性能改进算法.该算法首先使用BB步长算子调节收敛速度; 其次使用提出的下降VisuShrink阈值对重构图像进行筛选; 最后对重建图像进行循环平移以消除伪吉布斯效应.

2) 本文算法与IST、IST-TV和IST-CS算法的对比分析结果表明, 本文算法可以以较快的收敛速度重构一幅清晰的天文图像, 并且能有效地保护天文图像的细节特征.在压缩采样比较低时, 本文算法也可获得较优的重构效果.

3) 虽然本文算法的收敛速度和去噪重建性能得到很大的提高, 但是花费的重建时间较长, 因此如何提高本文算法的重建速度是以后改进的方向.