随着集成电路、信号与系统和功率转换器等的快速发展,带隙基准源在模拟和数字电路中起到了重要的作用[1-3],例如在AD转换器和DRAMs中的应用.一般数据转换器工作的温度范围是-40 ℃~125 ℃,12位编码器的温度系数为240×10-6和16位编码器温度系数为12×10-6.由于带隙基准电压几乎不受温度和电源电压变化的影响[4-6],系统的精度和抗干扰能力直接受基准电压的性能的影响,高性能的基准电压已成为电力、电子行业中关键技术之一.文献[7-8]介绍了几种带隙基准电压源,文献[7]提出的带隙基准源结构,利用MOSFETs工作在弱反型区产生的正负温度系数的电压相加得到的基准电压,虽然该结构可以减小功耗,但是由于MOSFETs工作在弱反型区漏极电流是温度函数.当温度变化时,基准电压温漂大,不能达到高精度的目的.文献[8]中提出的一种传统的带隙基准电压源,虽然通过增加三极管发射极面积减小运放的输入失调电压,但是该结构精度低温漂大.
由于传统的基准电压精度低和功耗大等缺点,本文基于传统带隙基准结构的基础上,首次提出了一种分段高阶曲率补偿的带隙基准电压源,利用工作在不同电流密度下的三极管的基极—发射极的压差作用在MOSFET的源—漏极,在MOSFET中产生具有温度特性电流,叠加到基准源上进行高阶补偿,实现低功耗、低温漂以及较低的线性调整率.
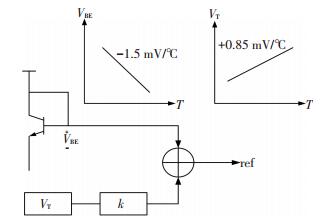
1 带隙基准的基本原理分析 1.1 带隙基准的基本原理分析传统带隙基准电压源基本原理如图 1所示,由于三极管的基极—发射极电压VBE的温度系数为-1.5 mV/℃,而热温度电压VT(=kT/q)温度系数为+0.085 mV/℃.其中k是Boltzmann常数(1.38×10-23 J/K), T是绝对温度,q是电子电荷量(1.6×10-19 J)[9].如果将具有正温度系数(PTAT)的电压VT和具有负温度系数(CTAT)的电压VBE相加,理论上可以得到与温度无关的基准电压,就可以抑制温度变化的影响[10-11].
|
图 1 带隙基准的基本原理 Figure 1 Basic principle of bandgap reference |
如果正温度系数电压按一定比例加上负温度系数电压,那么基准电压Vref可以表示为
| $ {V_{{\rm{ref}}}} = {V_{{\rm{BE}}}} + K{V_{\rm{T}}}, $ |
式中K为比例因子,那么基准电压的温度函数可以表示为
| $ \partial {V_{{\rm{ref}}}}/\partial T = \partial {V_{{\rm{BE}}}}/\partial T + K\partial {V_{\rm{T}}}/\partial T. $ |
只要合理的设置K值大小,理论上就可以得到零温度系数的带隙基准电压.但是传统结构的基准电压精度低温漂大,不能满足当今系统的设计要求,所以必须对带隙基准电压源进行温度补偿.
1.2 分段高阶曲率补偿原理由于传统的带隙基准源的温度特性曲线只有一个极值点,提高带隙基准电压精度的有效方法是使带隙基准电压的温度特性曲线具有多个极值点,而不是只有一个峰值或谷值.想要获得高精度的基准电压源,必须需要高阶的温度曲率补偿[12-13].一阶温度补偿仅仅可以补偿温度T的一次项,而仅仅通过传统的补偿技术不能达到基准电压的高阶温度曲率补偿,就不能获得高精度的带隙基准源.
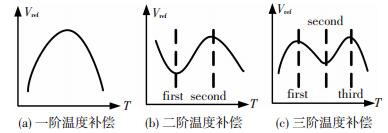
如图 2所示是利用补偿技术得到的带隙基准源的温度特性曲线.采用合适的补偿方法,在低温或者高温区域引入与基准电压的温度特性曲线呈相反趋势的补偿电流,使温度特性曲线在低温或高温区域产生新的极点.
|
图 2 高阶补偿的基本原理 Figure 2 The basic principle of high order compensation |
高阶补偿技术可以抵消温度T的高次项,通过高阶补偿可以得到高精度的基准电压源.理论上最好的方法是利用有Tln T的函数去补偿VBE的高阶非线性项,而Tln T函数在实际中很难获得,一般用近似的方法得到Tln T的函数,一般情况下是以Tln[T/Vref]的函数实现,Tln[T/Vref]补偿技术如图 2所示,Vref_first(second/third)是补偿的最优点,Tln[T/Vref]可以准确的抵消VBE的非线性项,如果补偿电压值电压大于或者小于Vref_first(second/third),将会出现补偿不够或者补偿过度,基准电压不能得到精确的补偿.只有选择合适的补偿电压,基准电压才能具有低的温度系数.
选择三极管是因为它有很好的温度特性[14],三极管的基极—发射极电压VBE可以表示为
| $ \begin{array}{l} {V_{{\rm{BE}}}}\left( T \right) = {V_{{\rm{G0}}}}({T_0})- [{V_{{\rm{G0}}}}({T_0})-{V_{{\rm{BE}}}}({T_0})]T/{T_0} -\\ \left( {\eta -\zeta } \right){\rm{ }}{V_{\rm{T}}}\ln (T/{T_0}). \end{array} $ |
式中:VG0(T0)为温度在T时的带隙基准电压; VBE(T0)为BJT管在温度T0时基极—发射极的压降; η为与温度无关而与工艺相关的常数; ζ为集电极电流随温度变化的指数; [VG0(T0)-VBE(T0)]T/T0为与温度相关的一次相; (η-ζ)VTln(T/T0)为高阶非线性相.在T0时刻将VTln(T/T0)泰勒展开得到:
| $ {V_{\rm{T}}}{\rm{ln}}\left( {\frac{T}{{{T_0}}}} \right) = \frac{k}{q}T\left[{\left( {\frac{T}{{{T_0}}}-1} \right)-\frac{1}{2} \times {{\left( {\frac{T}{{{T_0}}}-1} \right)}^2} + \frac{1}{3} \times {{\left( {\frac{T}{{{T_0}}} - 1} \right)}^3}} \right]. $ | (1) |
基于这一原理提出了如图 3所示的高阶曲率补偿的带隙基准电压源.
|
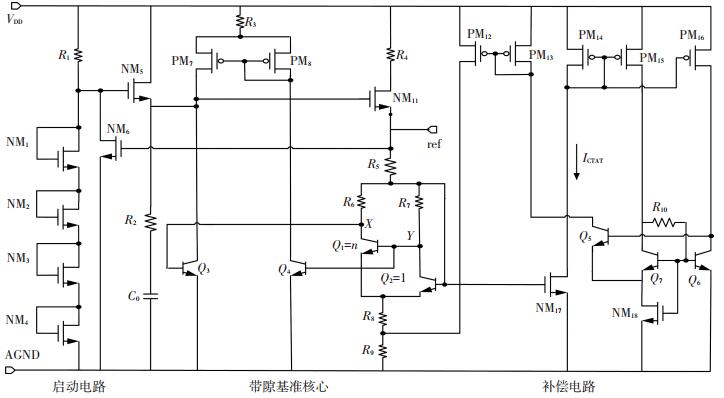
图 3 采用高阶曲率补偿方法设计的带隙基准电压源 Figure 3 The proposed bandgap reference with high order curvature compensated method |
本文提出的高阶曲率补偿带隙基准电压源由3个部分组成,分别为启动电路、带隙基准核心电路和补偿电路.
2.1 启动电路启动电路是带隙基准电压源中不可缺少的, 作用在于使带隙基准电路脱零工作点状态.如图 3所示,启动电路由NM1~NM6、R1、R2和C0组成.其中NM1~NM4构成二极管的连接方式,上电阶段,NM1~NM4处于线性工作区,随着电源电压的升高,NM5的栅极电压逐迅速升高而导通,电源电压通过NM5向基准注入电流,基准电路开始启动.启动完成后,随着基准电压的升高,NM6会把A点拉低而关闭NM5,基准启动结束.
2.2 基准核心电路本文设计基准产生电路如图 3所示,带隙基准的运算放大器是由Q3、Q4、R3、PM7和PM8组成,电路中的运放不需要额外的偏置电流源,可以减小基准的功耗,主要思想是利用反函数技术——跨导gmr和互阻gmc的函数,因为ΔVBE= VBE2-VBE1 gmr· gmc·ΔVBE =MΔVBE·gmc.ΔVBE可能产生非线性电流,跨导gmr可以抵消非线性电流并且产生需要的增益M.带隙基准的核心是由R5~R9、Q1和Q2组成,差放的两个输入端分解接在Q1的集电极和Q2的集电极,钳制X点和Y点的压差相等,三极管Q1和Q2的组成一种复合管的连接方式,Q1与Q2的基极—射极的压差ΔVBE作用在电阻R7上,产生正温度系数电流,由于电阻R6=R7,所以流过R6和R7的电流相等.设Q1和Q2的电流密度之比为n:1.基准电压Vref可以表示为
| $ {V_{{\rm{ref}}}} = {V_{{\rm{BE2}}}} + \frac{{2{V_{\rm{T}}}{\rm{ln}}n}}{{{R_8}}}({R_5} + {R_8} + {R_9}). $ |
电路中NM10接成源跟随器的形式,大幅度减小其输出阻抗,它为基准核心提供所需电流.
2.3 补偿电路本文提出的高阶补偿电路如图 3所示,由Q5~Q7、PM12~PM16、NM17、NM18和R10组成,主要机理是随着温度的升高,Q2基极的负温度系数电压作用在NM17的栅极,产生CTAT电流,根据MOS管的特性可知,NM17的漏极电流ICTAT可表示为
| $ {I_{{\rm{CTAT}}}} = \frac{1}{2}S{\frac{W}{L}_{{\rm{(NM17}})}}{\left( {{V_{{\rm{BE}}}} + \frac{{{V_{\rm{T}}}{\rm{ln}}n}}{{{R_5}}}\left( {{R_7} + {R_8}} \right)-{V_{{\rm{TH}}}}} \right)^2}, $ | (2) |
式中S为工艺常数.PM14~PM16组成电流镜结构,PM15和PM16的漏极电流可以表示为IPM15=αIPM14,IPM16=βIPM14,其中α=WL(PM15)/WL(PM14),β=WL(PM16)/WL(PM14).
由于Q6和Q7的有效发射截面积比为M:1,两者基极—射极的压差作用在NM18的漏极和源级,驱使NM18工作在线性区.NM18的漏极电流INM18可表示为
| $ {I_{{\rm{NM18}}}} = \frac{1}{2}S{\frac{W}{L}_{{\rm{(NM18)}}}}{\left( {{V_{{\rm{BE}}}}-{V_{{\rm{TH}}}}} \right)^2}\cdot\left( {1 + \lambda {V_{\rm{T}}}{\rm{ln}}\left( {M\frac{\alpha }{\beta }} \right)} \right). $ | (3) |
由于MOSFET的阈值电压VTH与温度成线性关系,可以表示成
| $ {V_{{\rm{TH}}}}T = {V_{{\rm{TH}}}}\left( {{T_0}} \right)-\mu \left( {T-{T_0}} \right). $ | (4) |
根据基尔霍夫定律(KCL)可知,结合式(1),式(2)~(4)展开,三极管Q5的集电极电流ICQ5可表示为
| $ {I_{{\rm{CQ5}}}} \approx {I_{{\rm{NM18}}}}-\alpha {I_{{\rm{CTAT}}}} =-a{T^4} + b{T^3} + c{T^2}-dT - e{T_1}, $ | (5) |
其中:
| $ \begin{array}{l} a = S\frac{W}{L}\cdot\frac{k}{{{q^2}}}\cdot\frac{{\left( {\eta- \zeta } \right)}}{{{T_0}}}[k\left( {{V_{{\rm{G0}}}}\left( {{T_0}} \right) + {V_{{\rm{BE}}}}\left( {{T_0}} \right)} \right) + \mu], \\ b = s\frac{W}{L}\cdot\frac{k}{q}\cdot\left[{\lambda \mu {\rm{ln}}\left( {M\frac{\alpha }{\beta }} \right) + \frac{{2k}}{{q{T_0}}}-\lambda {\rm{ln}}\left( {M\frac{\alpha }{\beta }} \right)\left( {{V_{{\rm{G0}}}}\left( {{T_0}} \right)-{V_{{\rm{BE}}}}\left( {{T_0}} \right)} \right)} \right], \\ c = S\frac{W}{L}\cdot\frac{k}{q}\cdot\frac{{{\rm{ln}}N\left( {{R_7} + {R_8}} \right)}}{{{R_5}}}\cdot{\rm{ }}\left( {{V_{{\rm{G}}0}}({T_0}) - {V_{{\rm{BE}}}}{T_0} + \mu {T_0}} \right), \\ d \approx \frac{1}{2}S\frac{W}{L}\cdot\frac{k}{q}[2\frac{{{R_7} + {R_8}}}{{{R_5}}}\left( {{V_{{\rm{G}}0}}\cdot{\rm{ln}}N + {\rm{ln}}N\cdot\mu {T_0}} \right)-\\ {\left( {{V_{{\rm{G0}}}}-{V_{{\rm{TH0}}}} + \mu {T_0}} \right)^2}\cdot\lambda {\rm{ln}}M\frac{\alpha }{\beta }], \\ e \approx \frac{1}{2}S\frac{W}{L}\cdot{\left( {{V_{{\rm{G0}}}} -{V_{{\rm{TH0}}}} + \mu {T_0}} \right)^2}\left( {1 -\ln \left( {M\frac{\alpha }{\beta }} \right)} \right). \end{array} $ |
式中:μ为阈值电压的温度相关系数;VTH0为MOSFET的衬底和源极电压的差值为零时的阈值电压.由此可以得出a、b、c、d和e是与温度无关的常数.根据式(2)、(3)可知,ICTAT和INM18都是负温度系数的电流,而INM18的比例系数大于ICTAT,随着温度升高, INM18下降速度要快于ICTAT,由式(5)可知基准电压源的补偿电流的穿越温度为T1, 在温度T≤T1时,补偿电流对基准电压Vref的温度特性曲线进行高阶补偿,减小基准电压的温度系数;当T>T1时,Q5处于截至区没有电流通过,ICQ5=0,综上所述,补偿电流可表示为
| $ {I_{{\rm{CQ5}}}} = \left\{ \begin{array}{l} -a{T^4} + b{T^3} + c{T^2}-dT-e{T_1}, T \le {T_1};\\ 0, T > {T_1}. \end{array} \right. $ |
通过调整PM14~PM16电流镜的比例和NM18的宽长比等参数,可以实现对穿越温度为T1的调节,补偿电流ICQ5注入到电阻R9,对基准的温度特性曲线进行高阶补偿,在高温时关闭补偿电流.经过补偿后的带隙基准电压Vref可表示为
| $ {V_{{\rm{ref}}}} = {V_{{\rm{BE2}}}} + 2\frac{{{V_{\rm{T}}}\ln n}}{{{R_2}}}\cdot({R_5} + {R_8} + {R_9}) + {I_{{\rm{CQ5}}}}\cdot{R_9}. $ |
高阶补偿电路由ICTAT为其提供偏置电流,它的大小决定了补偿电路的功耗,由于ICTAT具有负温度系数特性,高阶补偿电路的功耗随着温度的升高而减小.要实现补偿的最优化,在尽可能减少硬件开销的情况下,也要限制电路的功耗,并且使芯片面积达到最小,所以要合理的设置各个器件的参数以达到性能最优.
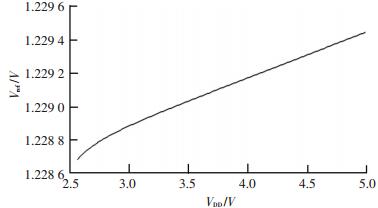
3 仿真结果本文带隙基准电压源仿真采用0.18 μm BCD工艺.利用Hspice仿真软件,温度在25 ℃,基准电压线性调整率仿真结果如图 4所示.仿真结果表明,基准电压的典型值为1.229 V.供电电压VDD在2.5~5.0 V范围内,线性调整率为0.033%.
|
图 4 基准电压随电源电压的变化曲线 Figure 4 Curve of reference voltage with power supply |
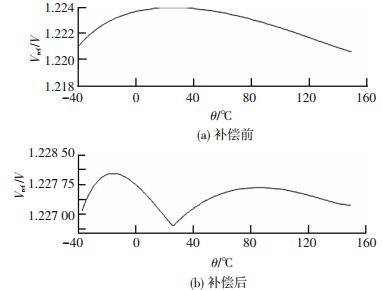
基准电压源的温度特性仿真结果如图 5所示,供电电压VDD为5 V,在-40 ℃~150 ℃的温度范围内,仿真结果表明,基准电压源补偿前的的温度系数为20×10-6/℃,补偿后的温度系数为6.94×10-6/℃,可以看出补偿后带隙基准电压源的温度特性得到明显的改善.
|
图 5 基准电压温度特性曲线 Figure 5 Temperature characteristic curve of reference voltage |
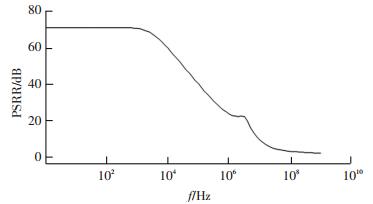
基准电压源的电源抑制比仿真结果如图 6所示,供电电压VDD为5 V,温度为25 ℃,仿真结果表明,低频时PSRR为77 dB,具有很好的抑制电源干扰的能力.
|
图 6 基准电压的PSRR仿真结果 Figure 6 The PSRR curves of reference voltage |
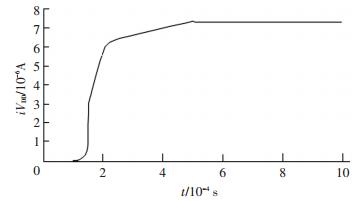
基准电压源功耗如图 7所示,从仿真结果可以看出,电路的静态电流功耗仅为7.36 μA,电路具有较低的功耗.
|
图 7 电路工作电流仿真结果 Figure 7 Simulation results of circuitworking current |
表 1为本文和文献[7-9]的参数性能的比较,从表 1中可以看出,基准电压源的温度系数明显优于文献[7-9],功耗远低于文献[8].
| 表 1 带隙基准的性能比较 Table 1 Performance comparison with references |
1) 本文对传统的带隙基准电压源结构进行改进, 提出了一种新型的高阶曲率补偿的带隙基准电压电路,该电路中采用了一种简单的补偿电路实现高阶曲率补偿,使基准电压的温度特性曲线呈现出多个极值点,克服了传统带隙基准电压带隙基准源的温度特性差的缺点,同时电路正常工作时需要较小的电流.虽然利用三极管占用较多的芯片面积,但性能优势是明显的.
2) 通过和传统的带隙基准电压源性能的对比,表明了高阶曲率补偿方法可以使基准电压源获得良好的温度特性,通过仿真对比,证明了所设计的补偿电路明显的提高了温度特性.结果表明, 各项指标性能满足设计要求.此基准电压源可以应用到对性能要求较为严格场合,如掌上电脑、第3代手机和GPS接收器等等.
| [1] |
PARK J S, AN T J, KIM Y M, et al. A 10b 50MS/s 90nm CMOS skinny-shape ADC using variable references for CIS applications[C]//2013 International Soc Design Conference. Busan, South Korea: IEEE, 2013: 80-82. DOI: 10.1109/ISOCC.2013.6863990.
|
| [2] |
FULDE M, WIMSHOFER M, KNOBLINGER G, et al. Design of low-voltage bandgap reference circuits in multi-gate CMOS technologies[C]//IEEE International Symposium on Circuits and Systems. Taipei, Taiwan: IEEE, 2009: 2537-2540. DOI: 10.1109/ISCAS.2009.5118318.
|
| [3] |
YANG Xinbo, DENG Honghui, QUAN Lei, et al. A differential reference voltage source and its output buffer used in high-speed high-precision pipelined ADC[C]//Proceedings of the 5th International Congress on Image and Signal Processing. Chongqing, China: IEEE, 2012:1398-1402. DOI: 10.1109/CISP.2012.6469818.
|
| [4] |
MA Jirong, LI Yongming, ZHANG Chun, et al. A 1V Ultra-low power high precision CMOS voltage reference[C] // IEEE Conference on Electron Devices and Solid-State Circuits. Tainan, Taiwan: IEEE, 2008: 847-850. DOI: 10.1109/EDSSC.2007.4450258.
|
| [5] |
李睿, 冯全源. 一种低功耗高精度带隙基准的设计[J].
电子技术应用, 2015, 41(3): 51-54.
LI Rui, FENG Quanyuan. Design of a bandgap reference voltage with low power consumption and high-accurary[J]. Application of Electronic Technique, 2015, 41(3): 51-54. DOI: 10.16157/j.issn.0258-7998.2015.03.012 |
| [6] |
WADHWA S K. A low voltage CMOS bandgap reference circuit[C]//International Symposium on Circuits and Systems. Seattle, WA: IEEE, 2008: 2693-2696. DOI: 10.1109/ISCAS.2008.4542012.
|
| [7] |
MOHAMMED M, ABUGHARBIEH K, ABDELFATTAH M, et al. Design of a voltage reference circuit based on subthreshold and triode MOSFETs in 90nm CMOS[C]//IEEE International Conference on Ic Design & Technology. Austin, TX: IEEE, 2014:1-4. DOI: 10.1109/ICICDT.2014.6838605.
|
| [8] |
唐宇, 冯全源. 一种低温漂低功耗带隙基准的设计[J].
电子元件与材料, 2014, 33(2): 35-38.
TANG Yu, FENG Quanyuan. Design of a bandgap reference with low temperature-drift and low power consumption[J]. Electronic Components and Materials, 2014, 33(2): 35-38. DOI: 10.3969/j.issn.1001-2028.2014.02.009 |
| [9] |
王宇星, 朱波. 一种用于PWM控制Buck型DC-DC变换器的带隙基准源[J].
电子器件, 2013, 36(2): 252-255.
WANG Yuxing, ZHU Bo. A CMOS bandgap reference for PWM control buck DC-DC converters[J]. Chinese Journal of Electron Devices, 2013, 36(2): 252-255. DOI: 10.3969/j.issn.1005-9490.2013.02.026 |
| [10] |
CHOUHAN SS, HALONEN K. A micro-power 4.8 ppm/℃ CMOS voltage reference circuit for linear drop out regulator used in RFID[C]//Proceedings of the 20th International Conference on Electronics, Circuits, and Systems. Abu Dhabi, United Arab Emirates: IEEE, 2013: 893-896. DOI: 10.1109/ICECS.2013.6815557.
|
| [11] |
TAN Xiaoyun, LIANG Chen, SHI Min, et al. A low temperature coefficient 4th-order curvature-compensated CMOS bandgap reference[C]// Academic International Symposium on Optoelectronics and Microelectronics Technology. Harbin, China: IEEE, 2011:251-254. DOI: 10.1109/AISMOT.2011.6159366.
|
| [12] |
DUAN Quanzhen, ROH J. A 1.2-V 4.2-ppm/℃ high-order curvature-compensated CMOS bandgap reference[J]. IEEE Transactions on Circuits and Systems Ⅰ: Regular Papers, 2015, 62(3): 662-670. DOI:10.1109/TCSI.2014.2374832.
|
| [13] |
PENG Zhenyu, LV Changzhi, SHE Shuojie. A High-order temperature curvature compensated CMOS bandgap reference[C]//Proceedings of the 2nd International Conference on Consumer Electronics, Communications and Networks. Yichang, China: IEEE, 2012: 2254-2257. DOI: 10.1109/CECNet.2012.6201536.
|
| [14] |
MA B, YU Fengqi. A novel 1.2-V 4.5-ppm/℃ curvature-compensated CMOS bandgap reference[J].
IEEE Transactions on Circuits Systems I: Regular Papers, 2014, 61(4): 1026-1035.
DOI: 10.1109/TCSI.2013.2286032 |
 2017, Vol. 49
2017, Vol. 49


