一架民用客机大约需要制150~-+ 200万个连接孔,其中不乏众多薄壁叠层结构装配连接孔.出于提高装配质量的考虑,装配孔一般需要合件加工,但由于钻削轴向力的作用,薄壁零件在制孔过程中存在着较大的层间间隙,间隙的存在会带来层间毛刺、切屑卷入层间等问题[1-2],这不仅会影响飞机装配质量、降低疲劳寿命[3],而且手工去除毛刺、切屑的过程,更是不利于飞机自动化装配过程的实现[4].因此,国内外专家学者们提出,在薄壁叠层结构制孔时,应使用预压紧技术使得叠层结构在钻孔过程中保持贴合.
HELLSTERN. C等[5]在叠层板钻削试验中在叠层板上加上一个的施加预压紧力的简易装置,使得层间毛刺得以减少. MELKOTE S N等[6]等通过对铝合金叠层结构的试验研究,认为压紧方式以及施加预压紧力的位置是影响钻削层间毛刺的主要因素. BI S S等[7-9]采用自制的机器人钻削设备,对TC4与Al-7075薄板叠层制孔过程中所产生的层间毛刺进行系统的试验研究,发现叠层制孔过程中所产生的毛刺不仅与工艺参数有关,还与叠层结构的夹持状态、叠层顺序有着很大联系. LI Y等[10]在不同的钻削参数和预压紧力下对铝合金叠层板进行钻削试验,认为轴向预压紧力比钻削参数对层间毛刺的抑制效果更显著. CHOI J等[11]通过有限元分析钻削过程中层间毛刺的形成过程,表明由于钻削轴向力而导致的层间间隙对层间毛刺的形成有着显著影响.卢志军[12]以制孔质量为约束条件,对铝合金薄壁叠层结构进行单向预压钻孔工艺研究,综合考虑孔圆柱度、夹层毛刺高度、效率等因素,提出工艺决策建议. LIANG J[13]尝试使用理论分析方法分析预压紧力对层间间隙的影响,将预压紧力作用下的钻削层间间隙模型,等效为简支梁受载弯曲模型进行分析,分析预压紧环对层间间隙的改变机理,并指出层间间隙与预压紧力、轴向力、材料刚度有关.陈威等[14]和徐溶蔚等[15]使用有限元法计算飞机蒙皮与长桁的刚度矩阵,并利用弹性力学的方法预测预压紧力数值.
施加预压紧力是为了减小叠层板制孔过程中的层间间隙,以达到降低层间毛刺形成空间、防止切屑卷入层间的目的.上述研究分析了预压紧力对加工质量的影响,未对其减小层间间隙的规律进行细致分析,并且未对所需施加的预压紧力数值进行探讨.考虑到层间间隙变化不易通过试验来获得,本文首先采用经典板壳理论建立叠层结构制孔简化模型,进而采用有限元方法,分析了预压紧力对叠层结构制孔层间间隙的影响,提出了通过临界预压紧力来确定最佳预压紧力数值的方法,并分析了轴向力、预压紧环直径、叠层组合、板厚比例对临界预压紧力的影响,并最终以试验的方法对有限元分析结果进行了验证.
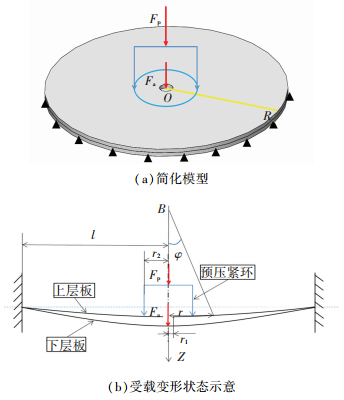
1 叠层结构制孔简化模型建立在飞机蒙皮的装配过程中,叠层板的厚度(t)一般小于5 mm,而相邻螺栓之间的间距(L)则超过100 mm,t/L=1/20<1/8,因此大多数飞机蒙皮的装配孔制备过程均为叠层薄板制孔.本文以板壳理论为基础对分析模型进行简化,图 1(a)为叠层结构制孔简化模型,模型四周采用刚性约束,轴向力采用点载荷进行施加,预压紧力采用圆形线载荷进行施加,圆形板半径OR为薄板中心至螺栓中心的距离. 图 1(b)是圆形叠层板受载弯曲变形示意图,Fa是制孔轴向力,Fp是预压紧力,其通过预压紧环施加于上层板,l=OR为圆形板半径,r1为钻孔半径,r2为预压紧环半径,r为板中性面上的点距离对称轴的距离(中性面是指板在厚度方向的对称面).
|
图 1 叠层结构制孔力学模型 Figure 1 Mechanical model of stacked material drilling |
根据铁摩辛柯板壳理论[16]可知,上层板(四周刚固中心带孔的圆形薄板)的弯曲变形方程:
当r1 < r < r2时
| $ \begin{array}{c} {Z_{\rm{u}}} = \frac{{{F_{\rm{p}}}}}{{16\pi M}}\cdot\{ ({l^2} + 4{\rm{ }}{r_2}^2{\rm{ln}}\frac{{{r_2}}}{l} - \frac{{{r_2}^4}}{{{l^2}}}) + \\ \frac{{{r_2}^2[2{\rm{ln}}({r_2}/l) + 1 - ({r_2}^2/{l^2})]}}{{\left( {1 + v} \right){r_1}^2 + \left( {1 - v} \right){r_2}^2}} \times [(1 - \\ v)({r^2} - {r_2}^2) + 2\left( {1 + v} \right){r_1}^2({\rm{ln}}\frac{r}{l} - {\rm{ln}}\frac{{{r_2}}}{l})]\} . \end{array} $ | (1) |
当r2 < r < l时
| $ {Z_{\rm{u}}} = \frac{{{F_{\rm{p}}}}}{{8\pi M}}\left[ {\left( {{r^2} + {r_2}^2} \right){\rm{ln}}\frac{r}{l} + \frac{1}{2}\left( {1 + \frac{{{r_2}^2}}{{{l^2}}}} \right)\left( {{l^2} - {r^2}} \right)} \right]. $ | (2) |
下层板(四周刚固的圆形薄板)弯曲变形方程为
| $ {Z_{\rm{d}}} = \frac{{{F_{\rm{a}}}}}{{32\pi M}}[2{l^2} - 2{r^2} + 4{r^2}{\rm{ln}}\frac{r}{l}]. $ | (3) |
式中M为薄板单位宽度上的刚度(N/m).
| $ M = [E{t^3}/12(1 - {v^2})]. $ | (4) |
式中:E为薄板弹性模量(MPa),v为泊松比,t为薄板板厚(mm),r为板中性面上的点距离对称轴的距离(mm).
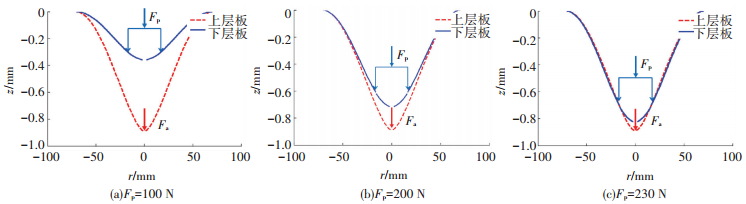
根据式(1)~(4)及表 1中的材料属性,结合实际制孔工艺,设定l=70 mm,r1=2 mm,r2=17.5 mm,t=1.5 mm,Fa=200 N,使用MATLAB软件对Al/Al叠层薄板弯曲变形过程进行数值模拟,结果如图 2所示.随着预压紧力从100 N增加至230 N,上层板的弯曲变形与下层板逐渐接近,并从最外围开始贴合,叠层薄板在受载弯曲变形过程中,其层间间隙有着先大幅减小,进而缓慢减小的过程,由于过大的预压紧力会造成叠层薄板过度弯曲变形,影响孔的形状精度,因而有必要通过计算,得出合理的预压紧力数值.由于数值模型无法模拟两板接触问题,下面使用有限元软件Abaqus对叠层薄板受载弯曲变形过程进行分析.
| 表 1 试验材料属性 Table 1 Test material properties |
|
图 2 预压紧力对Al/Al叠层薄板弯曲变形的影响(Fa=200 N) Figure 2 Effects of clamping force on deformation shape of Al/Al stacked thin plates (Fa=200 N) |
本文以典型的飞机蒙皮叠层结构Al/Al叠层、Al/Ti叠层作为分析对象. Al板、Ti板厚度t=1.5 mm,材料的属性见表 1.叠层板的接触采用面面接触属性,切向接触使用罚摩擦模型,该模型在切向摩擦力计算过程中,会自动选择罚刚度,并允许产生弹性滑动,适用于绝大多数接触问题;法向接触采用硬接触,当接触压力为负时,两接触体分离[17].有限元计算中,考虑到切削液的润滑作用,摩擦系数设定为0.3[18].
3D有限元模型采用有限元分析软件Abaqus建立,分析类型为Abaqus Standard准静态分析.叠层板采用两层板叠放结构,单层板尺寸为200 mm×200 mm,预压紧环直径35 mm,钻头直径4 mm,上层板采用通孔形式,距离薄板边缘50 mm处,预设螺栓孔4个,以螺栓孔孔壁刚固约束替代螺栓约束,有限元模型约束如图 3(a)所示. Al板模型采用5积分点SC8R连续壳单元.

|
图 3 有限元模型约束及载荷施加方式 Figure 3 Constraint and load applied way of finite element model |
叠层结构制孔层间间隙主要是由叠层板上下两层处于不同受力状态所形成.当钻头钻出上层板,进入下层板时,下层板受到钻削轴向力的挤压作用,沿钻头运动方向产生形变,因而上层板与下层板之间形成层间间隙.真实钻削过程的载荷较为复杂,本模型对预压紧力作用下的钻削过程进行简化,将载荷简化为两个部分,如图 3(b)所示.第一部分为钻削轴向力(Fa),通过对叠层板下层施加与钻头同样直径的圆形面载荷进行模拟;第二部分为预压紧力(Fp),其对叠层板的预压紧作用,通过对上层板施加环形面载荷进行模拟.
2.2 有限元模型验证叠层结构层间间隙形成时,预压紧力作用于上层板,钻削轴向力作用于下层板,两者相对独立,因此可以通过单层板受载弯曲变形试验,验证叠层结构制孔层间间隙有限元仿真模型的正确性.试验平台如图 4所示,试验板材采用尺寸为200 mm×200 mm×1.5 mm的铝合金板材,在距离薄板边缘50 mm处采用直径为8 mm的螺栓将板材固定,钢块平放于MTS CMT7000电子式万能试验机下部;预压紧环、钻头夹持于万能试验机上部.通过上部给定向下1 μm/s位移,获取薄板在载荷作用下的反作用力-位移曲线,并与有限元模型输出的反作用力-位移曲线(载荷施加位置)进行对比,以验证有限元模型的正确性.

|
图 4 单层Al板受载弯曲变形试验 Figure 4 Load-deformation test of single Al plate |
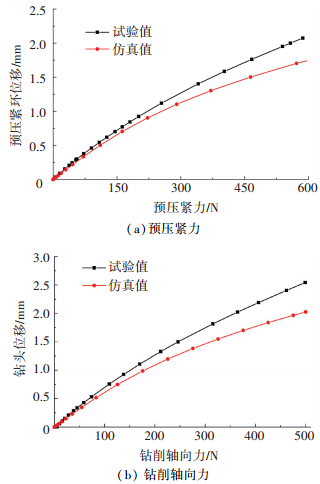
单层Al板在钻头载荷作用下弯曲变形状态如图 5所示.由图可知,有限元分析结果与试验结果基本吻合,再通过对比力-位移曲线(图 6)可知,无论是预压紧环挤压试验还是钻头挤压试验,其有限元仿真结果与试验结果在趋势、数量级上保持一致,但试验值的增长率一直大于有限元值的增长率.这是由于有限元仿真过程中未考虑支撑螺栓、预压紧环、钻头等系统的弯曲变形,而实际试验过程中这些部件也会随着载荷的增加而产生弹性弯曲变形,所以导致试验所测得的位移值大于仿真计算得出的位移值,并且其差值呈现逐渐增大的趋势.

|
图 5 Al板变形试验结果与模拟结果的对比 Figure 5 Comparison of experimental and simulation results of Al plate deformation state |
|
图 6 力-位移曲线试验结果与模拟结果的对比 Figure 6 Comparison of test and simulation values of load-displacement curve |
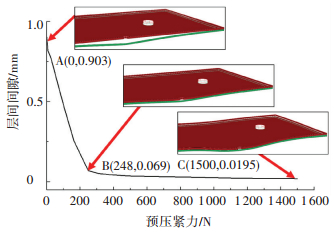
分析预压紧力对层间间隙的影响过程对研究预压紧力作用机理至关重要,从图 7可以看出,随着预压紧力的增加,叠层结构制孔间隙的减小过程可分为两个部分:
|
图 7 预压紧力对Al/Al叠层制孔层间间隙影响规律(Fa=200 N) Figure 7 Effect of clamping force on inter-layer gap formed in Al/Al stacked material drilling (Fa=200 N) |
第一部分为A-B段,即快速减少阶段,该阶段从预压紧力为0(A点)开始,至上层板与下层板贴合(B点)结束.此时对应的Fp为248 N,层间间隙由0.903 mm,缩小至0.069 mm,在此过程中每增加100 N预压紧力,层间间隙减少0.336 mm.在此阶段中,叠层板之间由于钻削轴向力的作用,存在着明显的间隙,此时预压紧力的作用效果较为明显.
第二部分为B~C段,即缓慢减少阶段,该阶段从上层板与下层板贴合(B点)开始,至预压紧力1500 N(C点)结束.该阶段,层间间隙由0.069 mm缩小至0.012 mm,层间间隙相比未施加预压紧力时,在此阶段,每增加100 N预压紧力,层间间隙仅减少0.004 mm.在此阶段中,由于上层板与下层板已处于接触状态,预压紧力的持续增大带来叠层板共同弯曲变形,由于上层板与下层板受力弯曲变形的差异,带来叠层间隙持续缓慢地减少.
因此,B点即为叠层板预压紧力作用的转折点,所对应的预压紧力FB称为临界预压紧力,是叠层结构制孔过程中适合预压紧力,此时对应的层间间隙为DB.
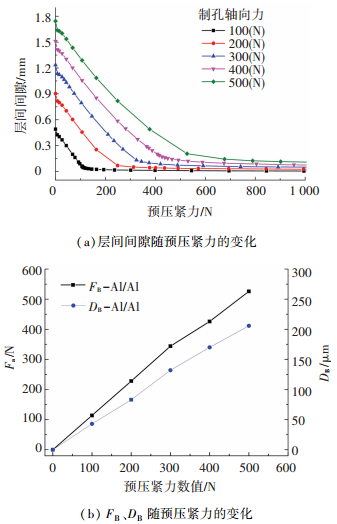
2.4 预压紧力转折点的主要影响因素分析 2.4.1 制孔轴向力对于层间间隙的影响分析不同钻头形式、制孔工艺会带来不同的制孔轴向力,而制孔轴向力对薄板弯曲变形状态也有影响. 图 8为不同轴向力作用下预压紧力对叠层结构制孔层间间隙的影响,如图 8(a)所示,对于Al/Al叠层结构,在不同的轴向力作用下,施加预压紧力均能够大幅度减少轴向间隙,但不同制孔轴向力情况下,预压紧力的作用效果则不相同.例如,100 N制孔轴向力情况下,1 000 N预压紧力能够将层间间隙缩减为原先的1%,而当制孔轴向力达到500 N时,1 000 N预压紧力能够将层间间隙缩减至原先的6%. 图 8(b)为不同制孔轴向力对叠层板临界预压紧力的影响,随着制孔轴向力的增加,FB与DB呈现线性增加的趋势,这是由于越大的轴向力带来越大的下层板弯曲变形,这时就需要更大的预压紧力使得叠层板达到贴合状态;由于下层板弯曲变形的非线性,越大的轴向力会造成带来钻头部位更加突出的弯曲变形,造成层间间隙增大.
|
图 8 不同轴向力作用下预压紧力对叠层制孔层间间隙的影响(Al/Al叠层) Figure 8 Effect of clamping force on inter-layer gap formed in stacked material drilling under different thrust force (Al/Al stacks) |
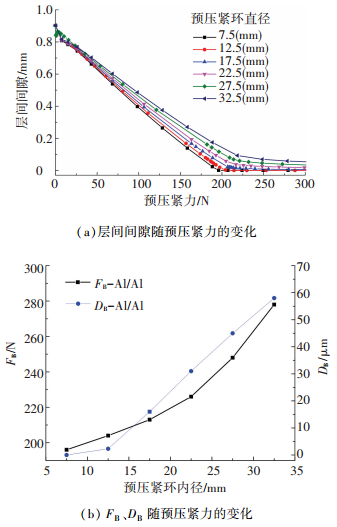
作为施加预压紧力的执行装置,预压紧环的直径大小直接影响着预压紧力的作用效果,如图 9预压紧环直径对叠层制孔层间间隙的影响所示,在制孔直径为4 mm时,相同预压紧环宽度的情况下,预压紧环直径由7.5 mm增加至32.5 mm,所需预压紧力FB由196 N增加至278 N,并且随着直径的增加,FB的增速越大;随着转折点的层间间隙DB由0 μm增加至55 μm,当预压紧环直径在7.5~12.5 mm时,DB增加缓慢,之后便呈现稳定的较快增加.这是由于预压紧环的直径减小,能够使得预压紧力作用位置与轴向力更为接近,这使得上层板的弯曲变形状态与下层板更加接近,从而降低FB与DB的值.
|
图 9 预压紧环直径对叠层制孔层间间隙的影响(Al/Al叠层;Fa=200 N;预压紧环宽度2.5 mm) Figure 9 Effect of the diameter of the preloading ring on inter-layer gap formed in stacked material drilling under different thrust force (Al/Al stacks; Fa=200 N; the width of the preloading ring is 2.5 mm) |
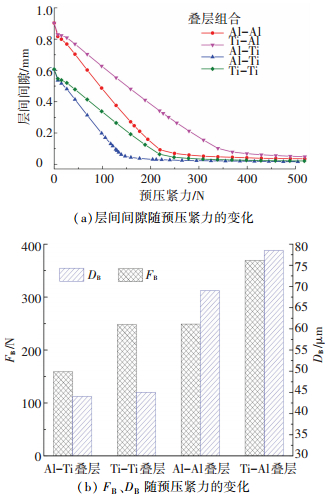
不同材料由于弹性模量、厚度等有所差异,抗弯曲变形能力也有所不同,因此不同材料组合的叠层结构在钻削时产生的层间间隙也有所不同.如图 10(a)所示,Ti-Al叠层与Al-Al叠层、Ti-Ti叠层与Al-Ti叠层在不施加预压紧力的情况下,其初始间隙是两两一致的,由此可见,在没有预压紧力作用下,决定叠层结构层间间隙的是下层板的弯曲变形状态,其不仅与板厚、制孔轴向力有关,也与下层板的材料属性有关,由于钛合金的弹性模量比铝合金大,所以其初始层间间隙也较小.
|
图 10 叠层组合对叠层板层间间隙的影响(Fa=200 N;t=1.5 mm;预压紧环直径32.5 mm) Figure 10 Effect of the stacked material types on inter-layer gap formed in stacked material drilling (Fa=200 N; t=1.5 mm; the diameter of the preloading ring is 32.5 mm) |
如图 10(b)所示,叠层结构下层板为Al时的层间间隙,明显高于下层板为Ti时的层间间隙;当叠层结构上下两层半为同一类型材料时,其FB值几乎相同;FB与DB值最大的叠层组合为Ti-Al叠层,该种情况下,下层板易弯曲变形,而上层板不易弯曲变形,造成预压紧力增加明显,层间间隙也不易减小.因此从提高制孔质量的角度考虑,应将弹性模量高的材料置于下层.
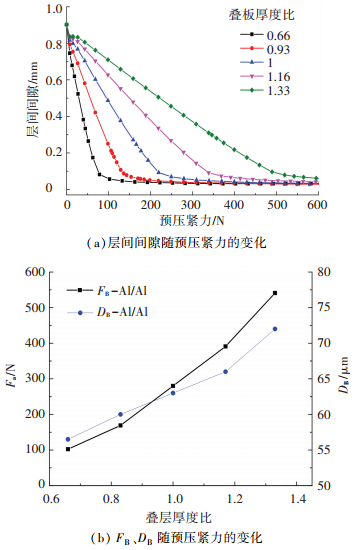
2.4.4 板厚比值对于层间间隙的影响分析在不同飞机蒙皮装配位置,叠层结构的上层板与下层板的厚度也会有所改变,而上层板与下层板厚度比值的变化必然会带来FB值与DB值的改变.由图 11(a)可见,在不同板厚比的情况下,预压紧力对层间间隙的减小过程是一致的;由图 11(b)所示,当厚度比从0.66增加至1.33的过程中,FB值由102 N迅速增加至541 N,并且增速随着板厚的增加而增加,这是由于施加预压紧力最主要的作用是使上层板与下层板在加工过程中保持贴合状态,而板厚比的增加使得上层板中性面刚度大于下层板中性面刚度,造成两板贴合难度加大;相比FB值的急剧增大,因此DB值仅由56 μm小幅增至72 μm,可见板厚比值主要是影响两板贴合的难易程度,而对最终贴合状态的影响不大.由此可见,增加上层板板厚,其影响最大的是FB值,由于过大的预压紧力会带来叠层结构的过度弯曲变形,因此为了减小所需的FB值,在制孔时应尽量将板厚较大的板材置于叠层结构下层.
|
图 11 叠层板厚比值对叠层制孔层间间隙的影响(Al/Al叠层;Fa=200 N;下层板板厚1.5 mm) Figure 11 Effect of thickness ratio of stacked plates on inter-layer gap formed in stacked material drilling (Al/Al stacks; Fa=200 N; lower plate thickness is 1.5 mm) |
通过上述有限元分析方法,可以获得叠层制孔时预压紧力施加的最佳数值,考虑加工过程中的层间间隙不易获取,因此可以通过监测叠层间毛刺高度,间接验证有限元分析结果的正确性.之所以选择层间毛刺高度作为层间间隙尺寸的判断指标,一方面是因为层间间隙会直接影响到层间毛刺的高度,另一方面层间毛刺本身也是评价叠层制孔质量的重要考核指标,过大的层间毛刺会对装配过程带来不利的影响.
试验设备为DH5570三坐标加工中心,钻头采用直径4 mm的硬质合金麻花钻,预压紧环直径15 mm,试验板材采用尺寸为200 mm×200 mm×1.5 mm的铝合金板材,材料属性如表 1所示,在距离薄板边缘50 mm处采用直径为8 mm的螺栓将板材固定.试验工装如图 12所示,预压紧力通过气缸进行施加,试验过程中改变气源压力以调节预压紧力大小.预压紧力大小通过Kistler 9272测力仪进行测量,钻削毛刺高度及宽度通过Sensofar白光共聚焦显微镜进行测量.在转速2500 rev/min及进给率0.1 mm/rev的切削参数下,钻削轴向力实测值为181 N,通过有限元计算,可知FB=210 N,DB=30 μm,因此预压紧力施加范围定为0~640 N,间隔为80 N.

|
图 12 试验现场 Figure 12 Experimental setup |
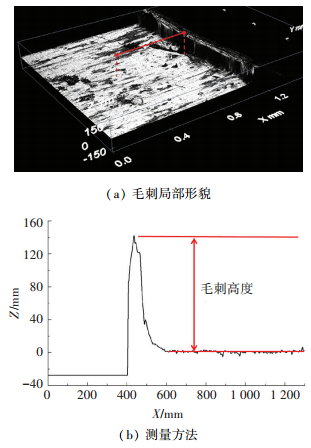
毛刺典型形态及测量方法如图 13所示,钻削毛刺的形成机理复杂、形状各异,入口毛刺主要是由于挤压隆起作用而导致的材料塑性弯曲变形,出口毛刺主要是由于底部支撑不足,最后一层材料并非切除,而是被钻头顶出,从而导致钻削出口处材料产生较大塑性弯曲变形[19].
|
图 13 Al合金孔出口毛刺形貌与测量方法 Figure 13 Exit burr morphology and measuring method of Aluminum Alloy hole |
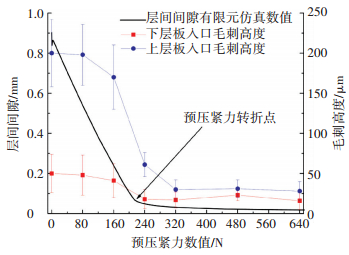
预压紧力的主要作用是改变层间间隙,因此其对层间毛刺的影响较大,选取上层板出口毛刺及下层板入口毛刺进行分析,结果见图 14所示.在0~160 N阶段,随着预压紧力的不断增大,层间毛刺高度并没有得到有效降低,这是由于此刻的层间间隙仍大于毛刺高度,预压紧力并没有起到限制毛刺生长的作用;当预压紧力介于160 N与320 N之间时,也就是层间间隙处于从300 μm向30 μm过度的过程中,较小的间隙形成了对层间毛刺的有效抑制作用,上层板出口、下层板入口毛刺高度降低明显;当预压紧力大于320 N时,由于层间间隙减小缓慢,增加预压紧力对毛刺的抑制效果明显减弱.可见,预压紧力的施加并不会影响钻削出口毛刺与钻削入口毛刺的形成机理,其主要是通过缩小层间间隙,减小毛刺的形成空间,使得上层板出口毛刺无法沿孔壁方向自由生长,而是抵住下层板进而切削去除,并且只有当预压紧力大于FB时,预压紧力才能起到明显的毛刺抑制作用.
|
图 14 预压紧力对层间毛刺尺寸的影响(0.1 mm/rev, 2 500 r·min-1) Figure 14 Effect of clamping force on inter-layer gap formed in stacked material drilling (0.1 mm/rev, 2500 r·min-1) |
本文采用有限元数值模拟与实验验证相结合的方法分析了飞机部件装配过程中,预压紧力对叠层结构制孔层间间隙的影响规律,具体结论如下:
1) 施加单向预压紧力可有效降低叠层制孔过程中的层间毛刺高度,且欲达到良好的毛刺抑制效果,预压紧力需满足以下两个条件:Ⅰ)其转折点对应的层间间隙DB需小于未施加预压紧力情况下的层间毛刺高度;Ⅱ)其值需高于临界预压紧力FB.
2) 减小制孔轴向力或预压紧环直径可有效降低临界预压紧力FB及对应层间间隙DB.
3) 叠层结构制孔过程中将尺寸较厚、模量较高的板材置于下层可进一步减小层间间隙、提高预压紧力作用效果.
| [1] |
姜丽萍, 陈文亮, 王珉, 等. 单向压紧制孔工艺的自适应响应面优化方法[J].
中国机械工程, 2015, 26(23): 3156-3161.
JIANG L P, CHEN W L, WANG M, et al. An approach to Adaptive Response Surface Optimization of One-side Pressed Drilling Process[J]. China Mechanical Engineering, 2015, 26(23): 3156-3161. DOI: 10.3969/j.issn.1005-132X.2015.23.007 |
| [2] |
王珉, 薛少丁, 陈文亮, 等. 面向飞机自动化装配的单向压紧制孔毛刺控制技术[J].
航空制造技术, 2011(9): 26-29.
WANG M, XUE S D, CHEN W L, et al. One-Side Pressed Burrless Drilling Technology for Aircraft Automatic Assembly[J]. Aeronautical Manufacturing Technology, 2011(9): 26-29. DOI: 10.16080/j.issn1671-833x.2011.09.020 |
| [3] |
SISCO T. Achieving "one up assembly" by reduction of interface burr height in aluminum, graphite, and advanced titanium/graphite hybrid (TiGr) material[R]. SAE Technical Paper. 2003. DOI: 10.4271/2003-01-2896.
|
| [4] |
DEVLIEG R, SITTON K, FEIKERT E, et al.ONCE (One-sided Cell End effector) Robotic Drilling System[R]. SAE Technical Paper. 2002. DOI: 10.4271/2002-01-2626.
|
| [5] |
HELLSTERN C. Investigation of interlayer burr formation in the drilling of stacked aluminum sheets[D]. Georgia Institute of Technology, 2009.
|
| [6] |
MELKOTE S N, NEWTON T R, HELLSTERN C, et al. Interfacial Burr Formation in Drilling of Stacked Aerospace Materials[M]. Berlin: Springer-Verlag. 2010.
|
| [7] |
BI S S, LIANG J. Experimental studies and optimization of process parameters for burrs in dry drilling of stacked metal materials[J].
The International Journal of Advanced Manufacturing Technology, 2011, 53(9-12): 867-876.
DOI: 10.1007/s00170-010-2877-y |
| [8] |
BI S S, LIANG J. Robotic drilling system for titanium structures[J].
The International Journal of Advanced Manufacturing Technology, 2011, 54(5-8): 767-774.
DOI: 10.1007/s00170-010-2962-2 |
| [9] |
LIANG J, BI S S. Design and experimental study of an end effector for robotic drilling[J].
The International Journal of Advanced Manufacturing Technology, 2010, 50(1-4): 399-407.
DOI: 10.1007/s00170-009-2494-9 |
| [10] |
LI Y, HU Y, Yao Z Q. Modeling and Analysis of the Effect of Preloaded Pressing Force on Gap Formation during the Drilling of Double-Layered Material[J].
Applied Mechanics & Materials, 2012, 217-219: 1541-1546.
DOI: 10.4028/www.scientific.net/AMM.217-219.1541 |
| [11] |
CHOI J, MIN S, DORNFELD D, et al. Modeling of inter-layer gap formation in drilling of a multi-layered material[R]. University of California at Berkeley, 2003.
|
| [12] |
卢志军. 制孔质量约束的铝合金薄壁叠层结构单向预压钻孔工艺研究[J].
航空制造技术, 2015, 495(S2): 152-156.
LU Z J. Study of One-Side Pressed Drilling Process of Aluminum Alloy Thin-Walled Laminated Structure[J]. Aeronautical Manufacturing Technology, 2015, 495(S2): 152-156. DOI: 10.16080/j.issn1671-833x.2015.S2.152 |
| [13] |
LIANG J. The formation and effect of interlayer gap in dry drilling of stacked metal materials[J].
The International Journal of Advanced Manufacturing Technology, 2013, 69(5-8): 1263-1272.
DOI: 10.1007/s00170-013-5112-9 |
| [14] |
陈威, 朱伟东, 章明, 等. 叠层结构机器人制孔压紧力预测[J].
浙江大学学报工学版, 2015, 49(12): 2282-2289.
CHEN W, ZHU W D, ZHANG M, et al. Clamping force prediction for robotic drilling of stacked structure[J]. Journal of Zhejiang University (Engineering Science), 2015, 49(12): 2282-2289. DOI: 10.3785/j.issn.1008-973X.2015.12.007 |
| [15] |
徐溶蔚, 王珉, 陈文亮. 基于响应面法的单向压紧制孔工艺参数优化[J].
航空制造技术, 2014(10): 68-71.
XU R W, WANG M, CHEN W L. Parameters Optimization of Automatic Skin-Side Pressed Drilling Process Based on the Response Surface Methodology[J]. Aeronautical Manufacturing Technology, 2014(10): 68-71. DOI: 10.16080/j.issn1671-833x.2014.10.020 |
| [16] |
铁摩辛柯.
板壳理论[M]. 北京: 科学出版社, 1977: 52-70.
TIMOSHENKO S P. Theory of Plates and Shells[M]. Beijing: Science Press, 1977: 52-70. |
| [17] |
张建伟, 等.
ABAQUS6.12有限元分析从入门到精通[M]. 北京: 机械工业出版社, 2015: 58-61.
ZHANG J W, et al. ABAQUS6.12 finite element analysis from entry to maste[M]. Beijing: China Machine Press, 2015: 58-61. |
| [18] |
刘悦. 高强铝合金摩擦行为及表征[D]. 秦皇岛: 燕山大学, 2011.
LIU Y. Friction Behaviors and Characterization of High Strength Aluminium Alloys[D]. Qinhuangdao: Yanshan University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10216-1012025713.htm |
| [19] |
KIM J, MIN S, DOENFELD D A. Optimization and control of drilling burr formation of AISI 304L and AISI 4118 based on drilling burr control charts[J].
International Journal of Machine Tools and Manufacture, 2001, 41(7): 923-936.
DOI: 10.1016/S0890-6955(00)00131-0 |
 2017, Vol. 49
2017, Vol. 49


