1. 哈尔滨工业大学 深圳研究生院, 广东 深圳 518055;
2. 深圳职业技术学院, 广东 深圳 518172
收稿日期: 2017-01-01
基金项目: 国家自然科学基金重大项目(61690210, 61690212);国家自然科学基金(61603111)
作者简介: 李建鹏(1991—), 男, 硕士研究生
Stability analysis and controller design for discrete-time systems with interval time-varying delays
1. Harbin Institute of Technology Shenzhen Graduate School, Shenzhen 518055, China;
2. Shenzhen Polytechnic, Shenzhen 518172, China
实际系统测量元件或测量过程中总是不可避免地存在信号传递时间延迟,这种现象普遍存在,也深受学者的广泛关注和研究[1].区间时变时滞是学者们的研究热点[2-5],而网络控制系统便是区间时变时滞动态系统的一个典型例子[6].利用频域法对时滞系统进行分析和设计,其求解并不容易,因而基于时域方法对时滞系统进行分析得到了广泛研究,特别是在系统存在不确定性时异常困难.时滞相关稳定性研究一般首先在时域空间内构造Lyapunov-Krasovskii泛函,通过模型变换以及交叉项界定技术或者自由权矩阵方法[7]得到系统稳定性的充分条件.其中自由权矩阵法直接对二次型积分项进行界定,避免了模型变换,获得了较小保守性的时滞相关稳定性条件[8].
具有区间时滞的离散系统的稳定性、镇定以及H∞控制问题同样也得到了广泛关注.文献[9]结合广义系统模型变换法和Moon不等式研究了离散系统的保代价控制问题.文献[10]研究了时变时滞离散系统输出反馈H∞控制问题.文献[11]应用自由权矩阵法求得时滞系统的稳定性判据.
本文结合增广型泛函[12]与时滞分割方法[13]构造新型的Lyapunov-Krasovskii泛函,在处理泛函过程中采用基于Abel引理的有限和不等式技术[14], 获得了保守性更小的稳定性分析结果.
1 问题描述 考虑离散时滞系统
|
$
\left\{ \begin{array}{l}
\mathit{\boldsymbol{x}}\left( {k + 1} \right) = \mathit{\boldsymbol{Ax}}\left( k \right) + {\mathit{\boldsymbol{A}}_d}\mathit{\boldsymbol{x}}\left( {k - d\left( k \right)} \right),\\
\mathit{\boldsymbol{x}}\left( k \right) = \varphi \left( k \right),k = - {h_M}, - {h_M} + 1, \cdots ,0.
\end{array} \right.
$
|
(1) |
式中:x(k)∈Rn为系统的状态向量,A, Ad∈Rn×n为恒定适维的系统矩阵,φ(k)为初始条件序列,时滞d(k)满足:
|
$
0 \le {h_m} \le d\left( k \right) \le {h_M}.
$
|
(2) |
设计状态反馈控制律
|
$
\mathit{\boldsymbol{u}}\left( k \right) = \mathit{\boldsymbol{Kx}}\left( k \right).
$
|
(3) |
系统(1)在控制器(3)的作用下得到如下闭环系统:
|
$
\left\{ \begin{array}{l}
\mathit{\boldsymbol{x}}\left( {k + 1} \right) = \mathit{\boldsymbol{Ax}}\left( k \right) + {\mathit{\boldsymbol{A}}_d}\mathit{\boldsymbol{x}}\left( {k - d\left( k \right)} \right) + {\mathit{\boldsymbol{B}}_u}\mathit{\boldsymbol{u}}\left( k \right),\\
\mathit{\boldsymbol{x}}\left( k \right) = \mathit{\boldsymbol{\varphi }}\left( k \right),k = - {h_M}, - {h_M} + 1, \cdots ,0.
\end{array} \right.
$
|
(4) |
首先分析系统(1)的稳定性条件,然后设计状态反馈控制器(3)使系统(4)渐近稳定.
为便于表述,现将文中用到的引理归纳如下.
引理 1[15] (Schur补性质) 给定分块矩阵
|
$
\mathit{\boldsymbol{S = }}\left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{S}}_{11}}}&{{\mathit{\boldsymbol{S}}_{12}}}\\
{\mathit{\boldsymbol{S}}_{12}^{\rm{T}}}&{{\mathit{\boldsymbol{S}}_{22}}}
\end{array}} \right].
$
|
则下述条件是等价的:
1) S < 0;
2) S11 < 0,S22-S12TS11-1S12 < 0;
3) S22 < 0, S11-S12S22-1S12T < 0.
引理 2[14] 对于常数矩阵R,R=RT>0以及整数r2-r1>1有下述不等式成立:
|
$
\sum\limits_{j = {r_1}}^{{r_2} - 1} {{\eta ^{\rm{T}}}\left( j \right)\mathit{\boldsymbol{R\eta }}\left( j \right)} \ge \frac{1}{{{\rho _1}}}\mathit{\boldsymbol{\nu }}_1^{\rm{T}}\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{\nu }}_1} + \frac{{3{\rho _2}}}{{{\rho _1}{\rho _3}}}\mathit{\boldsymbol{\nu }}_2^{\rm{T}}\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{\nu }}_2}.
$
|
其中
|
$
\begin{array}{l}
\mathit{\boldsymbol{\eta }}\left( j \right) = \mathit{\boldsymbol{x}}\left( {j + 1} \right) - x\left( j \right),{\rho _1} = {r_2} - {r_1},{\rho _2} = {r_2} - \\
{r_1} - 1,{\rho _3} = {r_2} - {r_1} + 1,{\mathit{\boldsymbol{\nu }}_1} = \mathit{\boldsymbol{x}}\left( {{r_2}} \right) - \mathit{\boldsymbol{x}}\left( {{r_1}} \right),{\mathit{\boldsymbol{\nu }}_2} = \\
\mathit{\boldsymbol{x}}\left( {{r_2}} \right) + \mathit{\boldsymbol{x}}\left( {{r_1}} \right) - \frac{2}{{{r_2} - {r_1} - 1}}\sum\limits_{j = {r_1} + 1}^{{r_2} - 1} {\mathit{\boldsymbol{x}}\left( j \right)} .
\end{array}
$
|
引理 3[16] 对于任意恒定适维矩阵Z>0及标量h2>h1>0,有下面不等式成立:
|
$
\sum\limits_{i = k - {h_2}}^{k - {h_1} - 1} {{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\left( i \right)\mathit{\boldsymbol{Z\omega }}\left( i \right)} \ge \frac{1}{{{h_{12}}}}{\left( {\sum\limits_{i = k - {h_2}}^{k - {h_1} - 1} {\mathit{\boldsymbol{\omega }}\left( i \right)} } \right)^{\rm{T}}}Z\left( {\sum\limits_{i = k - {h_2}}^{k - {h_1} - 1} {\mathit{\boldsymbol{\omega }}\left( i \right)} } \right).
$
|
2 主要结果 考虑系统(1),设N为大于零的正整数,利用hi, i=1, 2, …, N+1, 对时滞区间进行如下分割:
|
$
{h_m} = {h_1} < {h_2} < , \cdots , < {h_N} < {h_{N + 1}} = {h_M},
$
|
用δ表示子区间的长度:
|
$
\delta = \left\{ \begin{array}{l}
{h_{i + 1}} - {h_i} = \left\lfloor {\frac{{{h_M} - {h_m}}}{N}} \right\rfloor ,\;\;\;i = 1, \cdots ,N - 1;\\
{h_M} - {h_i},\;\;\;\;\;i = N.
\end{array} \right.
$
|
其中$\left\lfloor * \right\rfloor $表示向下取整.则有以下定理.
定理 1 对于给定的常数hm和hM,如果存在正定对称矩阵
|
$
\mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{P}}_{11}}}&{{\mathit{\boldsymbol{P}}_{12}}}&{{\mathit{\boldsymbol{P}}_{13}}}\\
* &{{\mathit{\boldsymbol{P}}_{22}}}&{{\mathit{\boldsymbol{P}}_{23}}}\\
*&* &{{\mathit{\boldsymbol{P}}_{33}}}
\end{array}} \right].
$
|
Qi,Zi,Ri,i=2, 3, 以及适当维数的自由矩阵Y使得如下线性矩阵不等式成立:
|
$
{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}_i} = \left[ {\begin{array}{*{20}{c}}
{{{\left[ {{\mathit{\boldsymbol{\varphi }}_{ij}}} \right]}_{6 \times 6}}}&{{\mathit{\boldsymbol{\theta }}^{\rm{T}}}{\mathit{\boldsymbol{P}}_{11}}}&{{\mathit{\pmb{\Upsilon}} ^{\rm{T}}}\mathit{\boldsymbol{U}}}\\
* &{ - {\mathit{\boldsymbol{P}}_{11}}}&0\\
*&* &{ - \mathit{\boldsymbol{U}}}
\end{array}} \right] < {\bf{0}},i = 1,2, \cdots ,N.
$
|
(5) |
则系统(1)是渐近稳定的.在式(5)中,
|
$
{\mathit{\boldsymbol{Y}}^{\rm{T}}} = \left[ {\begin{array}{*{20}{c}}
{\mathit{\boldsymbol{Y}}_1^{\rm{T}}}&{\mathit{\boldsymbol{Y}}_2^{\rm{T}}}&{\mathit{\boldsymbol{Y}}_3^{\rm{T}}}&{\mathit{\boldsymbol{Y}}_4^{\rm{T}}}&{\bf{0}}&{\bf{0}}
\end{array}} \right],
$
|
|
$
\mathit{\pmb{\Upsilon}} = \left[ {\begin{array}{*{20}{c}}
{\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{I}}}&{\bf{0}}&{{\mathit{\boldsymbol{A}}_d}}&{\bf{0}}&{\bf{0}}&{\bf{0}}
\end{array}} \right],
$
|
|
$
\mathit{\boldsymbol{\theta }} = \left[ {\begin{array}{*{20}{c}}
\mathit{\boldsymbol{A}}&{\bf{0}}&{{\mathit{\boldsymbol{A}}_d}}&{\bf{0}}&{\bf{0}}&{\bf{0}}
\end{array}} \right];
$
|
|
$
\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{\varphi }}_{11}} = - {\mathit{\boldsymbol{P}}_{11}} + {\mathit{\boldsymbol{A}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_{12}} + \mathit{\boldsymbol{P}}_{12}^{\rm{T}}\mathit{\boldsymbol{A}} + {\mathit{\boldsymbol{P}}_{22}} + {\mathit{\boldsymbol{Q}}_2} + {\mathit{\boldsymbol{Q}}_3} + }\\
{\frac{{1 - 2{h_i}}}{3}{\mathit{\boldsymbol{Z}}_2} - \frac{{2{h_i}}}{{{h_i} + 1}}{\mathit{\boldsymbol{R}}_2} - 2\frac{\delta }{{\delta + 1}}{\mathit{\boldsymbol{R}}_3};}
\end{array}
$
|
|
$
{\mathit{\boldsymbol{\varphi }}_{12}} = {\mathit{\boldsymbol{A}}^{\rm{T}}}\left( {{\mathit{\boldsymbol{P}}_{13}} - {\mathit{\boldsymbol{P}}_{12}}} \right) - {\mathit{\boldsymbol{P}}_{22}} + {\mathit{\boldsymbol{P}}_{23}} - \frac{{{h_i} + 1}}{3}{\mathit{\boldsymbol{Z}}_2};
$
|
|
$
{\mathit{\boldsymbol{\varphi }}_{13}} = \mathit{\boldsymbol{P}}_{12}^{\rm{T}}{\mathit{\boldsymbol{A}}_d} + {\mathit{\boldsymbol{Y}}_1},{\mathit{\boldsymbol{\varphi }}_{14}} = - {\mathit{\boldsymbol{A}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_{13}} - {\mathit{\boldsymbol{P}}_{23}} - {\mathit{\boldsymbol{Y}}_1};
$
|
|
$
{\mathit{\boldsymbol{\varphi }}_{15}} = {\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{I}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{P}}_{12}} + {\mathit{\boldsymbol{P}}_{22}} + {\mathit{\boldsymbol{Z}}_2} + \frac{2}{{{h_i} + 1}}{\mathit{\boldsymbol{R}}_2};
$
|
|
$
{\mathit{\boldsymbol{\varphi }}_{16}} = {\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{I}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{P}}_{13}} + {\mathit{\boldsymbol{P}}_{23}} + {\mathit{\boldsymbol{Z}}_2} + \frac{2}{{\delta + 1}}{\mathit{\boldsymbol{R}}_3};
$
|
|
$
\begin{array}{l}
{\mathit{\boldsymbol{\varphi }}_{22}} = {\mathit{\boldsymbol{P}}_{22}} - {\mathit{\boldsymbol{P}}_{23}} - \mathit{\boldsymbol{P}}_{23}^{\rm{T}} + {\mathit{\boldsymbol{P}}_{33}} + {\mathit{\boldsymbol{Q}}_2} - \frac{{2{h_i} + 5}}{3}{\mathit{\boldsymbol{Z}}_2} - \\
\;\;\;\;\;\;\;\;\frac{2}{{{h_i} - 1}}{\mathit{\boldsymbol{Z}}_2} + \frac{{1 - 2\delta }}{3}{\mathit{\boldsymbol{Z}}_3};
\end{array}
$
|
|
$
{\mathit{\boldsymbol{\varphi }}_{23}} = {\left( {{\mathit{\boldsymbol{P}}_{13}} - {\mathit{\boldsymbol{P}}_{12}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{A}}_d} + {\mathit{\boldsymbol{Y}}_2};
$
|
|
$
{\mathit{\boldsymbol{\varphi }}_{24}} = {\mathit{\boldsymbol{P}}_{23}} - {\mathit{\boldsymbol{P}}_{33}} - \frac{{\delta + 1}}{3}{\mathit{\boldsymbol{Z}}_3} - {\mathit{\boldsymbol{Y}}_2};
$
|
|
$
{\mathit{\boldsymbol{\varphi }}_{25}} = - {\mathit{\boldsymbol{P}}_{22}} + \mathit{\boldsymbol{P}}_{23}^{\rm{T}} + {\mathit{\boldsymbol{Z}}_2} + \frac{2}{{{h_i} - 1}}{\mathit{\boldsymbol{Z}}_2};
$
|
|
$
{\mathit{\boldsymbol{\varphi }}_{26}} = - {\mathit{\boldsymbol{P}}_{23}} + \mathit{\boldsymbol{P}}_{33}^{\rm{T}} + {\mathit{\boldsymbol{Z}}_3};
$
|
|
$
{\mathit{\boldsymbol{\varphi }}_{33}} = {\mathit{\boldsymbol{Y}}_3} + \mathit{\boldsymbol{Y}}_3^{\rm{T}};
$
|
|
$
{\mathit{\boldsymbol{\varphi }}_{34}} = - \mathit{\boldsymbol{A}}_d^{\rm{T}}{\mathit{\boldsymbol{P}}_{13}} - {\mathit{\boldsymbol{Y}}_3} + \mathit{\boldsymbol{Y}}_4^{\rm{T}};
$
|
|
$
{\mathit{\boldsymbol{\varphi }}_{35}} = \mathit{\boldsymbol{A}}_d^{\rm{T}}{\mathit{\boldsymbol{P}}_{12}},{\mathit{\boldsymbol{\varphi }}_{36}} = \mathit{\boldsymbol{A}}_d^{\rm{T}}{\mathit{\boldsymbol{P}}_{13}};
$
|
|
$
{\mathit{\boldsymbol{\varphi }}_{44}} = {\mathit{\boldsymbol{P}}_{33}} + {\mathit{\boldsymbol{Q}}_3} - \frac{{2\delta + 5}}{3}{\mathit{\boldsymbol{Z}}_3} - \frac{2}{{\delta - 1}}{\mathit{\boldsymbol{Z}}_3} - {\mathit{\boldsymbol{Y}}_4} - \mathit{\boldsymbol{Y}}_4^{\rm{T}};
$
|
|
$
{\mathit{\boldsymbol{\varphi }}_{45}} = - \mathit{\boldsymbol{P}}_{23}^{\rm{T}},{\mathit{\boldsymbol{\varphi }}_{46}} = - {\mathit{\boldsymbol{P}}_{33}} + {\mathit{\boldsymbol{Z}}_3} + \frac{2}{{\delta - 1}}{\mathit{\boldsymbol{Z}}_3};
$
|
|
$
{\mathit{\boldsymbol{\varphi }}_{55}} = - \frac{2}{{{h_i} - 1}}{\mathit{\boldsymbol{Z}}_2} - \frac{1}{{{h_s}}}{\mathit{\boldsymbol{R}}_2},{\mathit{\boldsymbol{\varphi }}_{56}} = 0;
$
|
|
$
{\mathit{\boldsymbol{\varphi }}_{66}} = - \frac{2}{{\delta - 1}}{\mathit{\boldsymbol{Z}}_3} - \frac{1}{{{h_d}}}{\mathit{\boldsymbol{R}}_3};
$
|
|
$
\begin{array}{l}
\mathit{\boldsymbol{U = }}\frac{{{h_i} + 1}}{6}h_i^2{\mathit{\boldsymbol{Z}}_2} + \frac{{\delta + 1}}{6}{\delta ^2}{\mathit{\boldsymbol{Z}}_3} + \frac{{{h_i}\left( {{h_i} + 1} \right)}}{2}{\mathit{\boldsymbol{R}}_2} + \\
\;\;\;\;\;\;\;\frac{{\delta \left( {\delta + 1} \right)}}{2}{\mathit{\boldsymbol{R}}_3};
\end{array}
$
|
|
$
{h_s} = \frac{{{h_i}\left( {{h_i} + 1} \right)}}{2},{h_d} = \frac{{\delta \left( {\delta + 1} \right)}}{2}.
$
|
证明 首先证明定理1在d(k)∈[h2, h3]子区间段时成立,进而将结论推广到一般的时滞区间中,即d(k)=[hi, hi+1](i=1, 2, …, N)时,定理1成立.
构造如下L-K泛函:
|
$
{\mathit{\boldsymbol{V}}_2}\left( k \right) = {\mathit{\boldsymbol{V}}_{21}}\left( k \right) + {\mathit{\boldsymbol{V}}_{22}}\left( k \right) + {\mathit{\boldsymbol{V}}_{23}}\left( k \right),
$
|
|
$
{\mathit{\boldsymbol{V}}_{21}}\left( k \right) = \mathit{\boldsymbol{\varepsilon }}_2^{\rm{T}}\left( k \right)\left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{P}}_{11}}}&{{\mathit{\boldsymbol{P}}_{12}}}&{{\mathit{\boldsymbol{P}}_{13}}}\\
* &{{\mathit{\boldsymbol{P}}_{22}}}&{{\mathit{\boldsymbol{P}}_{23}}}\\
*&* &{{\mathit{\boldsymbol{P}}_{33}}}
\end{array}} \right]{\mathit{\boldsymbol{\varepsilon }}_2}\left( k \right),
$
|
|
$
{\mathit{\boldsymbol{\varepsilon }}_2}\left( k \right) = {\left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right)}&{\sum\limits_{i = k - {h_2}}^{k - 1} {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right)} }&{\sum\limits_{i = k - {h_3}}^{k - {h_2} - 1} {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right)} }
\end{array}} \right]^{\rm{T}}},
$
|
|
$
\begin{array}{l}
{\mathit{\boldsymbol{V}}_{22}}\left( k \right) = \sum\limits_{i = k - {h_2}}^{k - 1} {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){Q_2}\mathit{\boldsymbol{x}}\left( i \right)} + \sum\limits_{i = k - {h_3}}^{k - 1} {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{Q}}_3}\mathit{\boldsymbol{x}}\left( i \right)} + \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{h_2}\left( {{h_2} + 1} \right)}}{6}\sum\limits_{\theta = - {h_2}}^{ - 1} {\sum\limits_{i = k + \theta }^{k + 1} {\mathit{\Delta } {x^{\rm{T}}}\left( i \right){Z_2}\mathit{\Delta } x\left( i \right)} } + \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\delta \left( {\delta + 1} \right)}}{6}\sum\limits_{\theta = - {h_3}}^{ - {h_2} - 1} {\sum\limits_{i = k + \theta }^{k - 1} {\mathit{\Delta } {x^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{Z}}_3}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( i \right)} } ,
\end{array}
$
|
|
$
\begin{array}{l}
{\mathit{\boldsymbol{V}}_{23}}\left( k \right) = \sum\limits_{m = - {h_2}}^{ - 1} {\sum\limits_{j = m}^{ - 1} {\sum\limits_{i = k + j}^{k - 1} {\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{R}}_2}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( i \right)} } } + \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{m = - {h_3}}^{ - {h_2} - 1} {\sum\limits_{j = m}^{ - 1} {\sum\limits_{i = k + j}^{k - 1} {\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{R}}_3}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( i \right)} } } .
\end{array}
$
|
对V2(k)做前向差分,则有:
|
$
\begin{array}{l}
\mathit{\Delta } {\mathit{\boldsymbol{V}}_{21}}\left( k \right) = \mathit{\boldsymbol{\varepsilon }}_2^{\rm{T}}\left( {k + 1} \right)\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{\varepsilon }}_2}\left( {k + 1} \right) - \mathit{\boldsymbol{\varepsilon }}_2^{\rm{T}}\left( k \right)\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{\varepsilon }}_2}\left( k \right) = \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;2\mathit{\boldsymbol{\varepsilon }}_2^{\rm{T}}\left( k \right)\mathit{\boldsymbol{P}}\mathit{\Delta } {\mathit{\boldsymbol{\varepsilon }}_2}\left( k \right) + \mathit{\Delta } \mathit{\boldsymbol{\varepsilon }}_2^{\rm{T}}\left( k \right)\mathit{\boldsymbol{P}}\mathit{\Delta } {\mathit{\boldsymbol{\varepsilon }}_2}\left( k \right),
\end{array}
$
|
其中:
|
$
\begin{array}{l}
\mathit{\Delta } {\mathit{\boldsymbol{\varepsilon }}_2}\left( k \right) = \\
{\left[ {\begin{array}{*{20}{c}}
{\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right)}&{{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right) - {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_2}} \right)}&{{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_2}} \right) - {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_3}} \right)}
\end{array}} \right]^{\rm{T}}},
\end{array}
$
|
|
$
\begin{array}{l}
\mathit{\Delta } {\mathit{\boldsymbol{V}}_{22}}\left( k \right) = {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right)\left( {{\mathit{\boldsymbol{Q}}_2} + {\mathit{\boldsymbol{Q}}_3}} \right)\mathit{\boldsymbol{x}}\left( k \right) - {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_2}} \right){\mathit{\boldsymbol{Q}}_2}\mathit{\boldsymbol{x}}\left( {k - {h_2}} \right)\\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_3}} \right){\mathit{\boldsymbol{Q}}_3}\mathit{\boldsymbol{x}}\left( {k - {h_3}} \right) + \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right)\left[ {\frac{{{h_2} + 1}}{6}h_2^2{\mathit{\boldsymbol{Z}}_2} + \frac{{\delta + 1}}{6}{\delta ^2}{\mathit{\boldsymbol{Z}}_3}} \right]\mathit{\Delta } \mathit{\boldsymbol{x}}\left( k \right) - \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{h_2}\left( {{h_2} + 1} \right)}}{6}\sum\limits_{i = k - h_2}^{k - 1} {\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{Z}}_2}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( i \right) - } \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\delta \left( {\delta + 1} \right)}}{6}\sum\limits_{i = k - {h_3}}^{k - {h_2} - 1} {\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{Z}}_3}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( i \right)} .
\end{array}
$
|
应用引理2,得到
|
$
\begin{array}{l}
\mathit{\Delta } {\mathit{\boldsymbol{V}}_{22}}\left( k \right) \le {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right)\left( {{\mathit{\boldsymbol{Q}}_2} + {\mathit{\boldsymbol{Q}}_3}} \right)\mathit{\boldsymbol{x}}\left( k \right) - {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - } \right.\\
\;\;\;\left. {{h_2}} \right){\mathit{\boldsymbol{Q}}_2}\mathit{\boldsymbol{x}}\left( {k - {h_2}} \right) - {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_3}} \right){\mathit{\boldsymbol{Q}}_3}\mathit{\boldsymbol{x}}\left( {k - {h_3}} \right) + \\
\;\;\;\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right)\left[ \begin{array}{l}
\frac{{{h_2} + 1}}{6}h_2^2{\mathit{\boldsymbol{Z}}_2} + \\
\;\;\;\;\;\;\frac{{\delta + 1}}{6}{\delta ^2}{\mathit{\boldsymbol{Z}}_3}
\end{array} \right]\mathit{\Delta } \mathit{\boldsymbol{x}}\left( k \right) + \\
\;\;\;\frac{{1 - 2{h_2}}}{3}{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right){\mathit{\boldsymbol{Z}}_2}\mathit{\boldsymbol{x}}\left( k \right) - \\
\;\;\;\frac{{2\left( {{h_2} + 1} \right)}}{3}{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right){Z_2}\mathit{\boldsymbol{x}}\left( {k - {h_2}} \right) + 2{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right){Z_2}\sum\limits_{i = k - {h_2}}^{k - 1} {\mathit{\boldsymbol{x}}\left( i \right)} - \\
\;\;\;\frac{{2{h_2} + 5}}{3}{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_2}} \right){\mathit{\boldsymbol{Z}}_2}\mathit{\boldsymbol{x}}\left( {k - {h_2}} \right) - \\
\;\;\;\frac{2}{{{h_2} - 1}}{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_2}} \right){\mathit{\boldsymbol{Z}}_2}\mathit{\boldsymbol{x}}\left( {k - {h_2}} \right) + \\
\;\;\;\left( {2 + \frac{4}{{{h_2} - 1}}} \right){\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_2}} \right){\mathit{\boldsymbol{Z}}_2}\sum\limits_{i = k - {h_2}}^{k - 1} {\mathit{\boldsymbol{x}}\left( i \right)} - \\
\;\;\;\frac{2}{{{h_2} - 1}}\sum\limits_{i = k - {h_2}}^{k - 1} {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{Z}}_2}} \sum\limits_{i = k - {h_2}}^{k - 1} {\mathit{\boldsymbol{x}}\left( i \right)} + \\
\;\;\;\frac{{1 - 2\delta }}{3}{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_2}} \right){\mathit{\boldsymbol{Z}}_3}\mathit{\boldsymbol{x}}\left( {k - {h_2}} \right) - \\
\;\;\;\frac{{2\left( {\delta + 1} \right)}}{3}{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_3}} \right){\mathit{\boldsymbol{Z}}_3}\mathit{\boldsymbol{x}}\left( {k - {h_3}} \right) + \\
\;\;\;2{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_2}} \right){\mathit{\boldsymbol{Z}}_3}\sum\limits_{i = k - {h_3}}^{k - {h_2} - 1} {\mathit{\boldsymbol{x}}\left( i \right)} - \\
\;\;\;\frac{{2\delta + 5}}{3}{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_3}} \right){\mathit{\boldsymbol{Z}}_3}\mathit{\boldsymbol{x}}\left( {k - {h_3}} \right) + \\
\;\;\;\left( {2 + \frac{4}{{\delta - 1}}} \right){\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_3}} \right){\mathit{\boldsymbol{Z}}_3}\sum\limits_{i = k - {h_3}}^{k - {h_2} - 1} {\mathit{\boldsymbol{x}}\left( i \right)} - \\
\;\;\;\frac{2}{{\delta - 1}}\sum\limits_{i = k - {h_3}}^{k - {h_2} - 1} {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right)} {\mathit{\boldsymbol{Z}}_3}\sum\limits_{i = k - {h_3}}^{k - {h_2} - 1} {\mathit{\boldsymbol{x}}\left( i \right)} - \\
\;\;\;\frac{2}{{\delta - 1}}{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_3}} \right){\mathit{\boldsymbol{Z}}_3}\mathit{\boldsymbol{x}}\left( {k - {h_3}} \right),\\
\;\;\;\mathit{\Delta } {\mathit{\boldsymbol{V}}_{23}}\left( k \right) = {h_s}\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right){\mathit{\boldsymbol{R}}_2}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( k \right) - \\
\;\;\;\sum\limits_{j = - {h_2}}^{ - 1} {\sum\limits_{i = k + j}^{k - 1} {\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{R}}_2}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( i \right)} } + \\
\;\;\;{h_d}\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right){\mathit{\boldsymbol{R}}_3}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( k \right) - \sum\limits_{j = - {h_3}i}^{ - {h_2} - 1} {\sum\limits_{i = k + j}^{k - 1} {\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{R}}_3}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( i \right)} } .
\end{array}
$
|
应用引理3,可得到:
|
$
\begin{array}{l}
\mathit{\Delta } {\mathit{\boldsymbol{V}}_{23}}\left( k \right) \le {h_s}\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right){\mathit{\boldsymbol{R}}_2}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( k \right) + {h_d}\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right){\mathit{\boldsymbol{R}}_3}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( k \right) - \\
\;\;\;\;\;\;\;\;\;\frac{1}{{{h_s}}}\left[ {h_2^2{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right){\mathit{\boldsymbol{R}}_2}\mathit{\boldsymbol{x}}\left( k \right) - 2{h_2}\sum\limits_{i = k - {h_2}}^{k - 1} {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{R}}_2}\mathit{\boldsymbol{x}}\left( k \right)} + } \right.\\
\;\;\;\;\;\;\;\;\;\left. {\sum\limits_{i = k - {h_2}}^{k - 1} {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{R}}_2}} \sum\limits_{i = k - {h_2}}^{k - 1} {\mathit{\boldsymbol{x}}\left( i \right)} } \right] - \frac{1}{{{h_d}}}\left[ {{\delta ^2}{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right){\mathit{\boldsymbol{R}}_3}\mathit{\boldsymbol{x}}\left( k \right) - } \right.\\
\;\;\;\;\;\;\;\;\;\left. {2\delta \sum\limits_{i = k - {h_3}}^{k - {h_2} - 1} {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{R}}_3}\mathit{\boldsymbol{x}}\left( k \right)} + \sum\limits_{i = k - {h_3}}^{k - {h_2} - 1} {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{R}}_3}} \sum\limits_{i = k - {h_3}}^{k - {h_2} - 1} {\mathit{\boldsymbol{x}}\left( i \right)} } \right],
\end{array}
$
|
|
$
\begin{array}{l}
\mathit{\Delta } {\mathit{\boldsymbol{V}}_2}\left( k \right) = \mathit{\Delta } {\mathit{\boldsymbol{V}}_{21}}\left( k \right) + \mathit{\Delta } {\mathit{\boldsymbol{V}}_{22}}\left( k \right) + \mathit{\Delta } {\mathit{\boldsymbol{V}}_{23}}\left( k \right) + \\
\;\;\;2{\eta ^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{Y}}\left[ {\mathit{\boldsymbol{x}}\left( {k - d\left( k \right)} \right) - \left( {k - {h_3}} \right) - } \right.\\
\;\;\;\left. {\sum\limits_{i = k - {h_3}}^{k - d\left( k \right) - 1} {\mathit{\Delta } \mathit{\boldsymbol{x}}\left( i \right)} } \right] \le {\eta ^{\rm{T}}}\left( k \right)\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} + {\mathit{\pmb{\Upsilon}} ^{\rm{T}}}\mathit{\boldsymbol{U}}\mathit{\pmb{\Upsilon}} + } \right.\\
\;\;\;\left. {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}^{\rm{T}}}{\mathit{\boldsymbol{P}}_{11}}\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \right)\eta \left( k \right).
\end{array}
$
|
基于Schur补引理,即可证得当i=2时定理1成立.
不失一般性,当d(k)∈[hi, hi+1], i=1, 2, …, N时,构造如下的L-K泛函:
|
$
\mathit{\Delta } {\mathit{\boldsymbol{V}}_i}\left( k \right) = {\mathit{\boldsymbol{V}}_{i1}}\left( k \right) + {\mathit{\boldsymbol{V}}_{i2}}\left( k \right) + {\mathit{\boldsymbol{V}}_{i3}}\left( k \right),
$
|
|
$
{\mathit{\boldsymbol{V}}_{i1}}\left( k \right) = \mathit{\boldsymbol{\varepsilon }}_i^{\rm{T}}\left( k \right)\left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{P}}_{11}}}&{{\mathit{\boldsymbol{P}}_{12}}}&{{\mathit{\boldsymbol{P}}_{13}}}\\
* &{{\mathit{\boldsymbol{P}}_{22}}}&{{\mathit{\boldsymbol{P}}_{23}}}\\
*&* &{{\mathit{\boldsymbol{P}}_{33}}}
\end{array}} \right]{\mathit{\boldsymbol{\varepsilon }}_i}\left( k \right),
$
|
|
$
\begin{array}{l}
{\mathit{\boldsymbol{V}}_{i2}}\left( k \right) = \sum\limits_{i = k - {h_i}}^{k - 1} {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{Q}}_2}x\left( i \right)} + \sum\limits_{i = k - {h_i} + 1}^{k - 1} {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{Q}}_3}x\left( i \right)} + \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{h_i}\left( {{h_i} + 1} \right)}}{6}\sum\limits_{\theta = - {h_i}}^{ - 1} {\sum\limits_{i = k + \theta }^{k - 1} {\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{Z}}_2}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( i \right) + } } \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\delta \left( {\delta + 1} \right)}}{6}\sum\limits_{\theta = - {h_i} + 1}^{ - {h_i} - 1} {\sum\limits_{i = k + \theta }^{k - 1} {\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{Z}}_3}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( i \right)} } ,
\end{array}
$
|
|
$
\begin{array}{l}
{\mathit{\boldsymbol{V}}_{i3}}\left( k \right) = \sum\limits_{m = - {h_i}}^{ - 1} {\sum\limits_{j = m}^{ - 1} {\sum\limits_{i = k + j}^{k - 1} {\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{R}}_2}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( i \right) + } } } \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{m = - {h_{i + 1}}}^{ - {h_i} - 1} {\sum\limits_{j = m}^{ - 1} {\sum\limits_{i = k + j}^{k - 1} {\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{R}}_3}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( i \right)} } } .
\end{array}
$
|
采用同样的方法可证明d(k)∈[hi, hi+1], i=1, 2, …,N时,系统(1)渐近稳定.
说明 1 定理1针对每一段时滞分割区间设计了新的L-K泛函,其中增广项Vi1(k), i=1, 2, …, N和三重求和项Vi3(k), i=1, 2, …, N, 充分利用了系统的时滞信息,为降低结论的保守性起到积极作用.在泛函差分处理过程中不涉及模型变换,而是利用文献[14]所提出的基于Abel引理的有限和不等式,直接给出Lyapunov泛函差分更紧的上界,因此可减少结论的保守性和计算的复杂性.
根据定理1可以进一步推导出使离散时滞系统(4)保持渐近稳定的镇定器设计方法.
定理 2 考虑离散时滞系统(4),给定时滞上下界hm、hM,如果存在正定对称矩阵
|
$
\mathit{\boldsymbol{\bar P}} = \left[ {\begin{array}{*{20}{c}}
\mathit{\boldsymbol{X}}&{{{\mathit{\boldsymbol{\bar P}}}_{12}}}&{{{\mathit{\boldsymbol{\bar P}}}_{13}}}\\
* &{{{\mathit{\boldsymbol{\bar P}}}_{22}}}&{{{\mathit{\boldsymbol{\bar P}}}_{23}}}\\
*&* &{{{\mathit{\boldsymbol{\bar P}}}_{33}}}
\end{array}} \right].
$
|
Qi,Zi,Ri,i=2, 3,X,J以及${\mathit{\boldsymbol{\hat K}}}$和适当维数的自由矩阵Y使得如下LMIs成立:
|
$
\begin{array}{l}
{{\mathit{\boldsymbol{ \boldsymbol{\bar \varXi} }}}_i} = \left[ {\begin{array}{*{20}{c}}
{{{\left[ {{{\mathit{\boldsymbol{\bar \varphi }}}_{ij}}} \right]}_{6 \times 6}}}&{\mathit{\boldsymbol{X}}{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}^{\rm{T}}}}&{\mathit{\boldsymbol{X}}{\mathit{\pmb{\Upsilon}}^{\rm{T}}}}&\mathit{\boldsymbol{ \boldsymbol{\bar \varGamma} }}&\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}\\
* &{ - \mathit{\boldsymbol{X}}}&{\bf{0}}&{\bf{0}}&{\bf{0}}\\
*&* &{\mathit{\boldsymbol{\bar U}} - 2\mathit{\boldsymbol{X}}}&{\bf{0}}&{\bf{0}}\\
*&*&* &{ - \mathit{\boldsymbol{J}}}&{\bf{0}}\\
*&*&*&* &{\mathit{\boldsymbol{J}} - 2\mathit{\boldsymbol{X}}}
\end{array}} \right] < 0,\\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1,2, \cdots ,N.
\end{array}
$
|
(6) |
则在如下状态反馈控制器的作用下系统(4)渐近稳定:
|
$
\mathit{\boldsymbol{u}}\left( k \right) = \mathit{\boldsymbol{Kx}}\left( k \right) = \mathit{\boldsymbol{\hat K}}{\mathit{\boldsymbol{X}}^{ - 1}}\mathit{\boldsymbol{x}}\left( k \right),
$
|
其中:
|
$
{\mathit{\boldsymbol{Y}}^{\rm{T}}} = \left[ {\begin{array}{*{20}{c}}
{\mathit{\boldsymbol{Y}}_1^{\rm{T}}}&{\mathit{\boldsymbol{Y}}_2^{\rm{T}}}&{\mathit{\boldsymbol{Y}}_3^{\rm{T}}}&{\mathit{\boldsymbol{Y}}_4^{\rm{T}}}&{\bf{0}}&{\bf{0}}
\end{array}} \right],
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\varTheta} }} = \left[ {\begin{array}{*{20}{c}}
{\mathit{\boldsymbol{A}} + {\mathit{\boldsymbol{B}}_u}\mathit{\boldsymbol{K}}}&{\bf{0}}&{{\mathit{\boldsymbol{A}}_d}}&{\bf{0}}&{\bf{0}}&{\bf{0}}
\end{array}} \right],
$
|
|
$
\mathit{\pmb{\Upsilon}} = \left[ {\begin{array}{*{20}{c}}
{A + {B_u}K}&0&{{A_d}}&{\bf{0}}&{\bf{0}}&{\bf{0}}
\end{array}} \right],
$
|
|
$
\mathit{\bar \Gamma } = {\left[ {\begin{array}{*{20}{c}}
{{{\bar P}_{12}}}&{{{\bar P}_{13}} -{{\bar P}_{12}}}&0&{ -{{\bar P}_{13}}}&{{{\bar P}_{12}}}&{{{\bar P}_{13}}}&{\bf{0}}&{\bf{0}}
\end{array}} \right]^{\rm{T}}},
$
|
|
$
\mathit{\Lambda = }{\left[ {\begin{array}{*{20}{c}}
{{{\left( {AX + {B_u}\hat K} \right)}^{\rm{T}}}}&{\bf{0}}&{\mathit{\boldsymbol{X}}{\mathit{\boldsymbol{A}}_d}}&{\bf{0}}&{\bf{0}}&{\bf{0}}&{\bf{0}}&{\bf{0}}
\end{array}} \right]^{\rm{T}}},
$
|
|
$
\begin{array}{l}
{{\mathit{\boldsymbol{\bar \varphi }}}_{11}} = - \mathit{\boldsymbol{X}} + {{\mathit{\boldsymbol{\bar P}}}_{22}} + {{\mathit{\boldsymbol{\bar Q}}}_2} + {{\mathit{\boldsymbol{\bar Q}}}_3} + \frac{{1 - 2{h_i}}}{3}{{\mathit{\boldsymbol{\bar Z}}}_2} - \frac{{2{h_i}}}{{{h_i} + 1}}{{\mathit{\boldsymbol{\bar R}}}_2} - \\
\;\;\;\;\;\;\;\;2\frac{\delta }{{\delta + 1}}{{\mathit{\boldsymbol{\bar R}}}_3},
\end{array}
$
|
|
$
{{\mathit{\boldsymbol{\bar \varphi }}}_{12}} = - {{\mathit{\boldsymbol{\bar P}}}_{22}} + {{\mathit{\boldsymbol{\bar P}}}_{23}} - \frac{{{h_i} + 1}}{3}{{\mathit{\boldsymbol{\bar Z}}}_2},{{\mathit{\boldsymbol{\bar \varphi }}}_{13}} = {{\mathit{\boldsymbol{\bar Y}}}_1},
$
|
|
$
{{\mathit{\boldsymbol{\bar \varphi }}}_{14}} = - {{\mathit{\boldsymbol{\bar P}}}_{23}} - {{\mathit{\boldsymbol{\bar Y}}}_1},{{\mathit{\boldsymbol{\bar \varphi }}}_{15}} = - {{\mathit{\boldsymbol{\bar P}}}_{12}} + {{\mathit{\boldsymbol{\bar P}}}_{22}} + {{\mathit{\boldsymbol{\bar Z}}}_2} + \frac{2}{{{h_i} + 1}}{{\mathit{\boldsymbol{\bar R}}}_2},
$
|
|
$
{{\mathit{\boldsymbol{\bar \varphi }}}_{16}} = - {{\mathit{\boldsymbol{\bar P}}}_{13}} + {{\mathit{\boldsymbol{\bar P}}}_{23}} + {{\mathit{\boldsymbol{\bar Z}}}_2} + \frac{2}{{\delta + 1}}{{\mathit{\boldsymbol{\bar R}}}_3},
$
|
|
$
\begin{array}{l}
{{\mathit{\boldsymbol{\bar \varphi }}}_{22}} = {{\mathit{\boldsymbol{\bar P}}}_{22}} - {{\mathit{\boldsymbol{\bar P}}}_{23}} - \mathit{\boldsymbol{\bar P}}_{23}^{\rm{T}} + {{\mathit{\boldsymbol{\bar P}}}_{33}} + {{\mathit{\boldsymbol{\bar Q}}}_2} - \frac{{2{h_i} + 5}}{3}{{\mathit{\boldsymbol{\bar Z}}}_2} - \\
\;\;\;\;\;\;\;\;\;\frac{2}{{{h_i} - 1}}{{\mathit{\boldsymbol{\bar Z}}}_2} + \frac{{1 - 2\delta }}{3}{{\mathit{\boldsymbol{\bar Z}}}_3},
\end{array}
$
|
|
$
{{\mathit{\boldsymbol{\bar \varphi }}}_{23}} = {{\mathit{\boldsymbol{\bar Y}}}_2},{{\mathit{\boldsymbol{\bar \varphi }}}_{24}} = {{\mathit{\boldsymbol{\bar P}}}_{23}} - {{\mathit{\boldsymbol{\bar P}}}_{33}} + \frac{{\delta + 1}}{3}{{\mathit{\boldsymbol{\bar Z}}}_3} - {{\mathit{\boldsymbol{\bar Y}}}_2},
$
|
|
$
\begin{array}{l}
{{\mathit{\boldsymbol{\bar \varphi }}}_{25}} = - {{\mathit{\boldsymbol{\bar P}}}_{22}} + \mathit{\boldsymbol{\bar P}}_{23}^{\rm{T}} + {{\mathit{\boldsymbol{\bar Z}}}_2} + \frac{2}{{{h_i} - 1}}{{\mathit{\boldsymbol{\bar Z}}}_2},{{\mathit{\boldsymbol{\bar \varphi }}}_{26}} = - {{\mathit{\boldsymbol{\bar \varphi }}}_{23}} + \\
\;\;\;\;\;\;\;\;\mathit{\boldsymbol{\bar P}}_{33}^{\rm{T}} + {{\mathit{\boldsymbol{\bar Z}}}_3},
\end{array}
$
|
|
$
{{\mathit{\boldsymbol{\bar \varphi }}}_{33}} = {{\mathit{\boldsymbol{\bar Y}}}_3} + \mathit{\boldsymbol{\bar Y}}_3^{\rm{T}},{{\mathit{\boldsymbol{\bar \varphi }}}_{34}} = - {{\mathit{\boldsymbol{\bar Y}}}_3} + {{\mathit{\boldsymbol{\bar Y}}}_4},{{\mathit{\boldsymbol{\bar \varphi }}}_{35}} = {{\mathit{\boldsymbol{\bar \varphi }}}_{36}} = 0,
$
|
|
$
{{\mathit{\boldsymbol{\bar \varphi }}}_{44}} = {{\mathit{\boldsymbol{\bar P}}}_{33}} + {{\mathit{\boldsymbol{\bar Q}}}_3} - \frac{{2\delta + 5}}{3}{{\mathit{\boldsymbol{\bar Z}}}_3} - \frac{2}{{\delta - 1}}{{\mathit{\boldsymbol{\bar Z}}}_3} - {{\mathit{\boldsymbol{\bar Y}}}_4} - \mathit{\boldsymbol{\bar Y}}_4^{\rm{T}},
$
|
|
$
{{\mathit{\boldsymbol{\bar \varphi }}}_{45}} = - \mathit{\boldsymbol{\bar P}}_{23}^{\rm{T}},{{\mathit{\boldsymbol{\bar \varphi }}}_{46}} = - {{\mathit{\boldsymbol{\bar P}}}_{33}} + {{\mathit{\boldsymbol{\bar Z}}}_3} + \frac{2}{{\delta - 1}}{{\mathit{\boldsymbol{\bar Z}}}_3},
$
|
|
$
{{\mathit{\boldsymbol{\bar \varphi }}}_{55}} = - \frac{2}{{{h_i} - 1}}{\mathit{\boldsymbol{Z}}_2} - \frac{1}{{{h_s}}}{\mathit{\boldsymbol{R}}_2},{{\mathit{\boldsymbol{\bar \varphi }}}_{56}} = 0,
$
|
|
$
{{\mathit{\boldsymbol{\bar \varphi }}}_{66}} = - \frac{2}{{\delta - 1}}{{\mathit{\boldsymbol{\bar Z}}}_3} - \frac{1}{{{h_d}}}{{\mathit{\boldsymbol{\bar R}}}_3},
$
|
|
$
\begin{array}{l}
\mathit{\boldsymbol{\bar U = }}\frac{{{h_i} + 1}}{6}h_i^2{{\mathit{\boldsymbol{\bar Z}}}_2} + \frac{{\delta + 1}}{6}{\delta ^2}{{\mathit{\boldsymbol{\bar Z}}}_3} + \frac{{{h_i}\left( {{h_i} + 1} \right)}}{2}{{\mathit{\boldsymbol{\bar R}}}_2} + \\
\;\;\;\;\;\;\;\frac{{\delta \left( {\delta + 1} \right)}}{2}{{\mathit{\boldsymbol{\bar R}}}_3}.
\end{array}
$
|
证明 用Ak=A+BuK替换定理1条件中的A,可得
|
$
{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}_i} = \left[ {\begin{array}{*{20}{c}}
{{{\left[ {{\mathit{\boldsymbol{\varphi }}_{ij}}} \right]}_{6 \times 6}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}^{\rm{T}}}{\mathit{\boldsymbol{P}}_{11}}}&{{\mathit{\pmb{\Upsilon}} ^{\rm{T}}}\mathit{\boldsymbol{U}}}\\
* &{ - {\mathit{\boldsymbol{P}}_{11}}}&{\bf{0}}\\
*&* &{ - \mathit{\boldsymbol{U}}}
\end{array}} \right] < {\bf{0}}\;\;i = 1,2, \cdots ,N.
$
|
(7) |
其中
|
$
\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{\varphi }}_{11}} = - {\mathit{\boldsymbol{P}}_{11}} + \mathit{\boldsymbol{A}}_k^{\rm{T}}{\mathit{\boldsymbol{P}}_{12}} + \mathit{\boldsymbol{P}}_{12}^{\rm{T}}{\mathit{\boldsymbol{A}}_k} + {\mathit{\boldsymbol{P}}_{22}} + {\mathit{\boldsymbol{Q}}_2} + {\mathit{\boldsymbol{Q}}_3} + }\\
{\frac{{1 - 2{h_i}}}{3}{\mathit{\boldsymbol{Z}}_2} - \frac{{2{h_i}}}{{{h_i} + 1}}{\mathit{\boldsymbol{R}}_2} - 2\frac{\delta }{{\delta + 1}}{\mathit{\boldsymbol{R}}_3},}
\end{array}
$
|
|
$
{\mathit{\boldsymbol{\varphi }}_{12}} = \mathit{\boldsymbol{A}}_k^{\rm{T}}\left( {{\mathit{\boldsymbol{P}}_{13}} - {\mathit{\boldsymbol{P}}_{12}}} \right) - {\mathit{\boldsymbol{P}}_{22}} + {\mathit{\boldsymbol{P}}_{23}} - \frac{{{h_i} + 1}}{3}{\mathit{\boldsymbol{Z}}_2},
$
|
|
$
{\mathit{\boldsymbol{\varphi }}_{14}} = - \mathit{\boldsymbol{A}}_k^{\rm{T}}{\mathit{\boldsymbol{P}}_{13}} - {\mathit{\boldsymbol{P}}_{23}} - {\mathit{\boldsymbol{Y}}_1},
$
|
|
$
{\mathit{\boldsymbol{\varphi }}_{16}} = {\left( {{\mathit{\boldsymbol{A}}_k} - I} \right)^{\rm{T}}}{\mathit{\boldsymbol{P}}_{13}} + {\mathit{\boldsymbol{P}}_{23}} + {\mathit{\boldsymbol{Z}}_2} + \frac{2}{{\delta + 1}}{\mathit{\boldsymbol{R}}_3},
$
|
|
$
{\mathit{\boldsymbol{\varphi }}_{15}} = {\left( {{\mathit{\boldsymbol{A}}_k} - I} \right)^{\rm{T}}}{\mathit{\boldsymbol{P}}_{12}} + {\mathit{\boldsymbol{P}}_{22}} + {\mathit{\boldsymbol{Z}}_2} + \frac{2}{{{h_i} + 1}}{\mathit{\boldsymbol{R}}_2},
$
|
|
$
\mathit{\pmb{\Upsilon}} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{A}}_k} - \mathit{\boldsymbol{I}}}&{\bf{0}}&\mathit{\boldsymbol{B}}&{\bf{0}}&{\bf{0}}&{\bf{0}}
\end{array}} \right],
$
|
|
$
\mathit{\boldsymbol{ \boldsymbol{\varTheta} }} = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{A}}_k}}&{\bf{0}}&\mathit{\boldsymbol{B}}&{\bf{0}}&{\bf{0}}&{\bf{0}}
\end{array}} \right].
$
|
${\left[ {{\mathit{\boldsymbol{\varphi }}_{ij}}} \right]_{6 \times 6}}$中其它项与定理1中的${\left[ {{\mathit{\boldsymbol{\varphi }}_{ij}}} \right]_{6 \times 6}}$相同.将式(7)左乘mat=diag{I, I, P11U-1},右乘matT得到
|
$
\left[ {\begin{array}{*{20}{c}}
{{{\left[ {{\mathit{\boldsymbol{\varphi }}_{ij}}} \right]}_{6 \times 6}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}^{\rm{T}}}{\mathit{\boldsymbol{P}}_{11}}}&{{\mathit{\pmb{\Upsilon}} ^{\rm{T}}}{\mathit{\boldsymbol{P}}_{11}}}\\
* &{ - {\mathit{\boldsymbol{P}}_{11}}}&{\bf{0}}\\
*&* &{ - {\mathit{\boldsymbol{P}}_{11}}{\mathit{\boldsymbol{U}}^{ - 1}}{\mathit{\boldsymbol{P}}_{11}}}
\end{array}} \right] < {\bf{0}};\;\;i = 1,2, \cdots ,N.
$
|
由于
|
$
- {\mathit{\boldsymbol{P}}_{11}}{\mathit{\boldsymbol{U}}^{ - 1}}{\mathit{\boldsymbol{P}}_{11}} \le \mathit{\boldsymbol{U}} - 2{\mathit{\boldsymbol{P}}_{11}}.
$
|
则有下面不等式成立:
|
$
\left[ {\begin{array}{*{20}{c}}
{{{\left[ {{\mathit{\boldsymbol{\varphi }}_{ij}}} \right]}_{6 \times 6}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}^{\rm{T}}}{\mathit{\boldsymbol{P}}_{11}}}&{{\mathit{\pmb{\Upsilon}} ^{\rm{T}}}{\mathit{\boldsymbol{P}}_{11}}}\\
* &{ - {\mathit{\boldsymbol{P}}_{11}}}&{\bf{0}}\\
*&* &{\mathit{\boldsymbol{U}} - 2{\mathit{\boldsymbol{P}}_{11}}}
\end{array}} \right] < {\bf{0}};\;\;i = 1,2, \cdots ,N.
$
|
(8) |
将式(8)左右同乘
|
$
{\rm{diag}}\left\{ {\mathit{\boldsymbol{P}}_{11}^{ - 1},\mathit{\boldsymbol{P}}_{11}^{ - 1},\mathit{\boldsymbol{P}}_{11}^{ - 1},\mathit{\boldsymbol{P}}_{11}^{ - 1},\mathit{\boldsymbol{P}}_{11}^{ - 1},\mathit{\boldsymbol{P}}_{11}^{ - 1},\mathit{\boldsymbol{P}}_{11}^{ - 1},\mathit{\boldsymbol{P}}_{11}^{ - 1}} \right\},
$
|
并令X=P11-1,${\mathit{\boldsymbol{\hat K}}}$=KP11-1,Δ=P11-1ΔP11-1,其中Δ代表任意矩阵,可得:
|
$
\left[ {\begin{array}{*{20}{c}}
{{{\left[ {{{\mathit{\boldsymbol{\bar \varphi }}}_{ij}}} \right]}_{6 \times 6}}}&{\mathit{\boldsymbol{P}}_{11}^{ - 1}{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}^{\rm{T}}}}&{\mathit{\boldsymbol{P}}_{11}^{ - 1}{\mathit{\pmb{\Upsilon}} ^{\rm{T}}}}\\
* &{ - \mathit{\boldsymbol{P}}_{11}^{ - 1}}&{\bf{0}}\\
*&* &{\mathit{\boldsymbol{\bar U}} - 2\mathit{\boldsymbol{P}}_{11}^{ - 1}}
\end{array}} \right] + \mathit{\boldsymbol{ \boldsymbol{\bar \varGamma} }}{\mathit{\boldsymbol{P}}_{11}}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{\rm{T}}} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{P}}_{11}}{{\mathit{\boldsymbol{ \boldsymbol{\bar \varGamma} }}}^{\rm{T}}} < 0.
$
|
(9) |
其中i=1, 2, …, N,因为
|
$
\mathit{\boldsymbol{ \boldsymbol{\bar \varGamma} }}{\mathit{\boldsymbol{P}}_{11}}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{\rm{T}}} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{P}}_{11}}{{\mathit{\boldsymbol{ \boldsymbol{\bar \varGamma} }}}^{\rm{T}}} \le \mathit{\boldsymbol{ \boldsymbol{\bar \varGamma} }}{\mathit{\boldsymbol{J}}^{ - 1}}{{\mathit{\boldsymbol{ \boldsymbol{\bar \varGamma} }}}^{\rm{T}}} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{P}}_{11}}\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{P}}_{11}}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{\rm{T}}}.
$
|
应用矩阵的Schur补性质可知式(9)等价于式(6),因此定理2得证.
3 仿真算例 例 1 考虑时变时滞离散系统:
|
$
\begin{array}{l}
\mathit{\boldsymbol{x}}\left( {k + 1} \right) = \left[ {\begin{array}{*{20}{c}}
{0.8}&0\\
{0.05}&{0.9}
\end{array}} \right]\mathit{\boldsymbol{x}}\left( k \right) + \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}}
{ - 0.1}&0\\
{ - 0.2}&{ - 0.1}
\end{array}} \right]\mathit{\boldsymbol{x}}\left( {k - d\left( k \right)} \right).
\end{array}
$
|
给定时滞下限hm,利用定理1得到的时滞上限hM列于表 1中.
表 1

表 1 给定hm使系统稳定的hM
Table 1 hM guaranteeing the stability of the system for given hm
| 方法 |
hm |
6 |
10 |
15 |
20 |
25 |
| 文献[17] |
hM |
14 |
15 |
18 |
22 |
26 |
| 文献[18] |
hM |
14 |
17 |
20 |
24 |
29 |
| 定理1(N=2) |
hM |
16 |
19 |
23 |
26 |
31 |
| 定理1(N=3) |
hM |
19 |
22 |
24 |
27 |
32 |
|
表 1 给定hm使系统稳定的hM
Table 1 hM guaranteeing the stability of the system for given hm
|
例 2 考虑如下时滞系统
|
$
\begin{array}{*{20}{c}}
{\mathit{\boldsymbol{x}}\left( {k + 1} \right) = \left[ {\begin{array}{*{20}{c}}
{0.5}&{0.3}\\
{0.2}&1
\end{array}} \right]\mathit{\boldsymbol{x}}\left( k \right) + \left[ {\begin{array}{*{20}{c}}
{0.1}&{0.4}\\
{0.2}&{0.1}
\end{array}} \right]\mathit{\boldsymbol{x}}\left( {k - } \right.}\\
{\left. {d\left( k \right)} \right) + \left[ {\begin{array}{*{20}{c}}
1\\
1
\end{array}} \right]\mathit{\boldsymbol{u}}\left( k \right).}
\end{array}
$
|
当初始值为x(0)=[-2 2]T,$d\left(k \right) = \left\lfloor {7.1 + 4\sin \left(k \right)} \right\rfloor $时,系统开环响应曲线如图 1所示.
对于给定的时滞下界hm,运用定理2,选取N=2可得到保证系统渐近稳定的时滞上界hM以及控制器K,分别列于表 2中.
表 2

表 2 给定时滞下限时滞上界及控制器增益
Table 2 Delay upper bound and controller gain for given delay lower bound
| hm |
hM |
控制器增益K |
| 2 |
12 |
[-0.331 3 -0.722 0] |
| 5 |
13 |
[-0.345 6 -0.744 2] |
| 8 |
15 |
[-0.381 1 -0.769 3] |
| 11 |
18 |
[-0.420 8 -0.819 7] |
|
表 2 给定时滞下限时滞上界及控制器增益
Table 2 Delay upper bound and controller gain for given delay lower bound
|
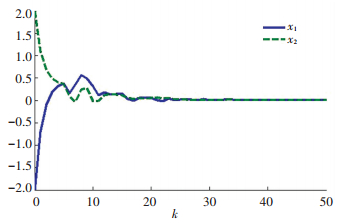
假设系统初始值为x(0)=[-2 2]T,状态时滞为$d\left(k \right) = \left\lfloor {7.1 + 5\sin \left(k \right)} \right\rfloor $,根据表 2求得的反馈控制器K=[-0.331 3 -0.722 0],对应的闭环响应曲线如图 2所示.
4 结论 基于一种新的时滞分割方法,研究了一类区间时变时滞离散系统的稳定性分析和状态反馈控制器设计问题,得到新的低保守性结果.具体而言,在构造L-K泛函时,使用了增广型泛函和时滞分割相结合的方法,在泛函的差分处理过程中借助于基于Abel引理的有限和不等式技术保证了结论具有较小的保守性.在数值仿真算例中,通过与以往结果进行比较,验证了所得的结果正确和有效.

 2017, Vol. 49
2017, Vol. 49


