电子束焊接发展至今已有近70年的历史,由于其具有能量密度高、焊后变形小、焊缝质量高等优点,该技术被广泛应用于航空、航天、核能、交通运输及国防等高新技术制造领域[1-2].对于焊接过程,焊缝成形质量是焊后残余应力、变形的影响因素之一,所以,焊后成形的检测与分析十分重要,而焊接熔池的流动过程对焊缝成形起着至关重要的作用.但是,现在焊接领域还没有提出一个完善的焊缝成形评判标准.
近年来,很多研究者利用数值模拟的方法来研究熔池流动对焊缝成形的影响规律.罗怡等[3]建立三维瞬态模型研究了电子束焊接镁合金时的温度场,证明利用热效应计算焊接形貌特征的合理性;霍宏伟[4]建立了移动热源作用下三维瞬态熔池模型, 比较在不同焊接条件下,熔池的形态变化. S.J.Na等[5-6]对高能束焊接过程中匙孔与熔池间的热力耦合过程进行了模拟与分析;武传松等[7]对不同焊接方法进行模拟研究,分析熔池流动的力学行为.尽管有许多学者对于中厚板深熔焊进行了研究,但由于节能环保的迫切需要,铝合金应用于航空航天、汽车及军工领域的焊接结构趋向于轻量化,所以,铝合金薄板焊接的研究受到广泛关注.
铝合金薄板电子束焊后成形可控性差、质量低,本文基于Fluent利用VOF算法建立三维瞬态EBW模型,对2 mm厚的2219铝合金板的温度场和流场进行模拟,研究了熔池的流动行为.本研究对铝合金薄板电子束焊接焊后成形控制具有重要意义.
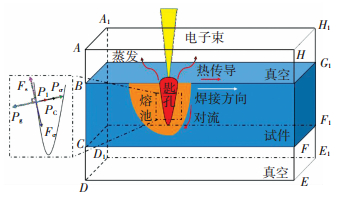
1 EBW有限元模型的建立 1.1 熔池分析和基本假设图 1为电子束焊接传热方式及受力过程的示意图.对于熔池而言,金属受高速电子束冲击而受热熔化,熔池表面金属迅速蒸发,造成热量损失;液态金属快速流动,对熔池边界形成“冲刷作用”,以对流的方式进行导热;由于熔池温度较高,对环境产生辐射散热.对于未熔化的金属而言,主要以辐射方式进行散热,因为电子束焊接在真空下进行,所以不考虑工件表面对流换热.
|
图 1 电子束焊接示意 Figure 1 Sketch map of electron beam welding |
电子束焊接过程中会产生匙孔效应,在匙孔壁面法线方向上,液态金属主要受反冲压力、液态金属静压力以及弯曲液面产生的附加压力作用;在匙孔壁面切线方向上,液态金属主要受表面张力所产生的切向力以及金属蒸汽与匙孔壁面摩擦产生的剪切力作用.
在电子束焊接过程中,各个物理过程十分剧烈,全部考虑不太现实,在模拟过程中需要将某些对实际焊接影响不大的过程进行简化处理,所以,作了如下假设:1)试件初始温度为300K;2)忽略金属蒸汽摩擦力对焊接熔池的影响[8];3)材料各向同性,除密度、比热容、粘度、导热系数是温度的函数外,其余热物性参数都是常数;4)焊接熔池内部流动形式为层流.
1.2 控制方程与物理模型在计算流体力学中,焊接熔池要满足流体流动三大方程,即连续性方程、动量守恒方程和能量守恒方程.在动量守恒方程中以表面张力、热浮力、重力、金属蒸汽反冲压力作为源项,在能量守恒方程中以电子束热源、熔化焓、汽化焓作为源项.
利用VOF算法追踪焊接熔池自由表面,引入流体体积分数函数F,F满足方程
| $ {V_f}\frac{{\partial F}}{{\partial t}} + \nabla \left( {A\cdot U} \right) = 0. $ | (1) |
式中:Vf为网格流体体积分数;A为表面网格流体面积分数,A=(Ax,Ay,Az);U为网格流体速度.
金属蒸汽反冲压力采用Semak V提出的反冲压力模型[9],电子束焊接热源采用旋转高斯体热源[10],它们分别为:
| $ {P_r} = 0.54{p_0}{\rm{exp}}\left( {\Delta {H_v}\frac{{T - {T_v}}}{{RT\;{T_v}}}} \right), $ | (2) |
| $ {q_r} = \frac{{3{c_s}Q}}{{\pi H(1 - {e^{ - 3}})}}{\rm{exp}}\left[ {\frac{{ - 3{c_s}}}{{{\rm{log}}\left( {\frac{H}{z}} \right)}}({x^2} + {y^2})} \right]. $ | (3) |
式中:Pr为反冲压力,p0为标准大气压,ΔHv为汽化潜热,Tv为材料汽化温度,R为理想气体常数;qr为电子束功率密度;Q为电子束功率,H为热源深度,cs为热源形状系数,(x2+y2)为熔池中任意点距离电子束中心的径向距离.
在反冲压力作用下,匙孔壁面发生弯曲,弯曲液面所产生的附加压力ΔP为[11]
| $ \Delta P = {\sigma _{\rm{T}}}\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right). $ | (4) |
式中:σT为温度T时的表面张力,R1、R2分别为曲面的两个主曲率半径.
非等温流动现象引起的热浮力Fb为
| $ {F_b} = ({\rho _{\rm{T}}} - {\rho _0})g{\rm{ }}. $ | (5) |
式中ρ0和ρT分别为熔点和温度T时液态金属的密度.
1.3 网格划分与材料属性本文采用2 mm厚的2219铝合金进行电子束焊接,其热物性参数通过文献[12]查得,如表 1所示.
| 表 1 2219铝合金热物性参数[12] Table 1 Physical properties of 2219 aluminum alloy and initial values |
电子束加速电压为60 KV,电子束流10 mA,焊接速度10 mm/s.模型尺寸为13 mm×4 mm×3 mm,金属板位于计算区域中心,在金属板上下各设置0.5 mm的自由液面变化区域.利用ICEM对模型划分网格,在近焊缝区采用加密网格,在远离焊缝区采用疏松网格.最小网格尺寸为0.083 mm,网格总数为162 864,节点总数174 270,计算区域外围采用outflow边界条件.计算域初始温度300 K,环境压力为0.
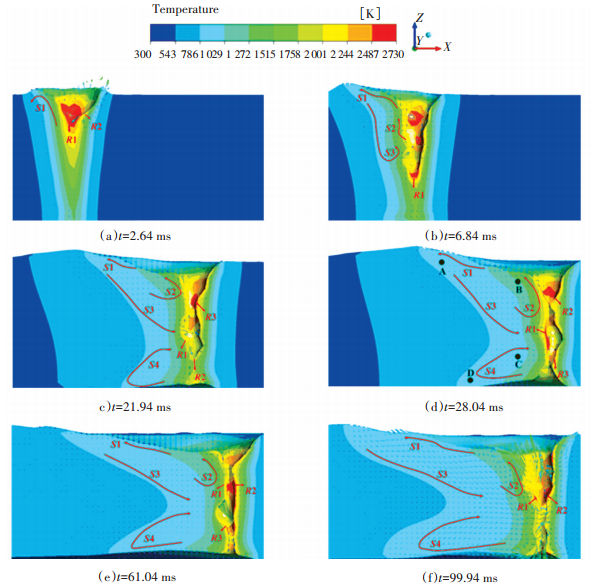
2 结果分析与讨论 2.1 温度场与流场的数值模拟图 2为电子束焊接深穿过程纵截面的温度和流场分布,其中S和R分别代表表面张力和反冲压力所引起的流动.从图中可看出,电子束穿透焊初始阶段与未穿透类似,如图 2(a)、(b),在匙孔深穿过程中,熔池表面金属蒸汽反冲压力大于表面张力,开始形成匙孔,随着匙孔壁面温度的升高,反冲压力增大,表面张力减小,匙孔尺寸继续增大,熔池内部液态金属受重力和匙孔壁面反冲压力作用向R1、R2方向流动;而匙孔壁面温度较高,上方熔池表面温度较低,在负的表面张力梯度作用下,匙孔表面液态金属产生S1和S2方向的流动.
|
图 2 熔池纵截面温度场与流场随时间的变化 Figure 2 Calculated temperature fields and flow fields in a longitudinal-section side views |
如图 2(c)所示,在21.94 ms时匙孔深度达到板厚的3/4,由于匙孔表面温度梯度大,表面张力和反冲压力大小分布不均匀,匙孔表面十分不稳定.对于熔池上部,尾部液态的金属对匙孔附近的过热金属有“拖拽”作用,形成S1和S2方向的流动,这也是熔池长度增加的主要原因,液态金属向熔池后方流动过程中受到固液界面的阻碍而回流,形成S3方向的流动,一部分汇入S2再次回流至熔池表面,一部分流向匙孔,这样就不断地把匙孔壁面附近的过热金属的能量传递给上表面熔池的左后方,使上部分熔池被拉长.匙孔下方过热金属在反冲压力R1、R2的作用下向熔池尾部流动,受到固液界面的阻碍而向S4方向流,S3与S4在熔池中部汇合共同流向匙孔,同样,过热金属的能量被传递给下表面熔池的左后方,使下部分熔池被拉长.在28.04 ms时,金属板第一次被穿透,匙孔深度达到最大.如图 2(e)、(f),熔池被焊穿后,直到熔池达到准稳态,熔池内部的流动规律与28.04 ms时类似,只是熔池上、下表面长度发生了改变,不再赘述.熔池长度随时间的变化见图 3.当t=90 ms时,熔池长度趋于稳定,此时,焊接过程进入准稳态,稳定后的平均尺寸分别为4.842 mm和3.787 mm.

|
图 3 熔池长度随焊接时间的变化 Figure 3 Simulation results of molten pool length evolution |
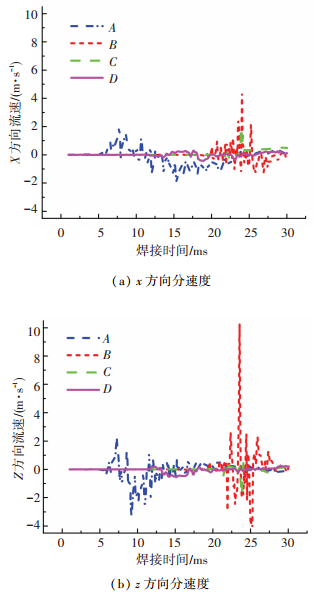
在28.04 ms时选取熔池中4个典型位置进行分析,图 4是它们在0~30 ms范围内流速随时间的变化.
|
图 4 点A、B、C、D流速随时间变化曲线 Figure 4 Calculated velocity evolution curves of point A、B、C、D (dimension of x-and z-axes) |
从这些点在x方向的流速变化曲线中可以看出,当焊接热源分别经过点A、B、C、D时(分别对应10 ms、23 ms、23 ms和15 ms),流速达到最大值,并且速度方向发生明显改变.其中,速度最大可以达到4 m/s,这是由于匙孔壁面温度梯度大,产生较强的Marangoni对流和反冲压力造成的,这说明电子束深穿焊接时,匙孔的形成不仅可以改变流速的大小,还可以改变流动的方向.因为点A、B位于金属板上半部分,热源经过它们时可以使A、B两点位于匙孔壁面,这两处流体受作用效果相反的表面张力和反冲压力驱动,所以A、B两点流速变化范围大;而热源经过点C、D时,匙孔深度没有达到C、D位置,这两处流体流动的主要驱动力是表面张力,所以C、D两点流速变化范围小.把A、B与C、D对比来看,A、B在-x方向产生的速度分量比C、D的大,液态金属在熔池中的“冲刷”作用更明显,所以上方熔池的拖尾比下方更长.
从图 4中点A、B、C、D在z方向的流速变化曲线中可看出,当A、B处于匙孔壁面上时,z方向速度大小迅速增大,速度方向周期性改变,使焊接熔池小范围内上下震荡,其中,最大流速可达到10 m/s;当A、B、C、D处于熔池内部、z方向上仅受重力和表面张力所引起的Marangoni对流作用时,纵向上的流速很小,上下波动十分平稳,这说明在电子束焊接熔池中,反冲压力的作用远远大于重力和表面张力的影响.这个结果也与文献[13]中得出的结论一致.
30 ms之后,点A、B、C、D与匙孔的间距越来越大,温度逐渐降低,趋向凝固,流速趋近于0,所以在图 4中不再呈现.
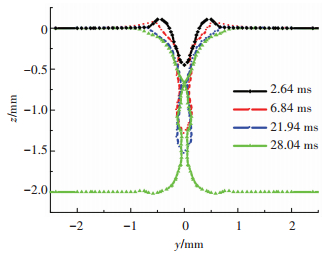
图 5是从图 1中提取的匙孔横截面演变曲线,它可以更好地表现出匙孔形状与尺寸的变化.在匙孔形成的初级阶段,由于熔池边缘处温度刚刚超过熔点,液态金属粘度较大,对匙孔内排出的过热金属起到阻碍作用,因此过热金属在熔池上方形成一定的堆积高度.可以发现,随着匙孔深度的增加,金属堆积的高度有所减小,这是由于焊接开始时,匙孔中的液态金属被排出到焊接起始点后端,对于整条焊缝而言,相当于“损失”了一部分金属,因此堆积量高度有所减小;随着焊接的进行,虽然匙孔深度的增加,排出的液态金属更多,但熔池表面积也迅速增大,排出的液态金属迅速在表面张力的作用下铺满整个熔池,凝固后形成焊缝余高,因此熔池上方的液态金属堆积高度继续降低;在焊接熔池达到准稳态前,熔池表面积不断增大,熔池表面的温度梯度也迅速增加,所以在熔池表面产生了更为强烈的Marangoni对流,上、下表面液态金属迅速由熔池中心流向熔池边缘,因此匙孔上、下开口半径不断增大,这也是焊接过程中熔宽的形成机理.
|
图 5 匙孔壁面形y状随时间的变化 Figure 5 The calculated keyhole wall versus time |
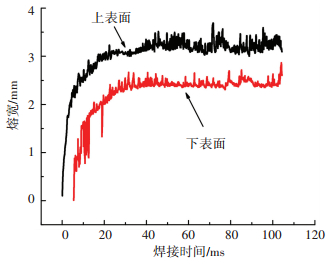
图 6是熔池宽度随焊接时间的变化,可以看出:t=5.46 ms时,金属板背面开始被熔透,t=35 ms时,上、下表面熔池宽度达到稳定,稳定后的平均熔池宽度分别为3.219 mm、2.451 mm,熔池宽度相对于熔池长度更早地进入准稳状态.
|
图 6 熔池宽度随时间的变化 Figure 6 The calculated pool width versus time |
将模拟的熔池边界与焊缝的横截面形貌进行对比,如图 7所示.可以看出,模拟的焊缝熔化线形状与实际焊缝熔化线形状和尺寸接近,因此可以验证本文采用热源模型的合理性.

|
图 7 模拟与实验横截面形貌对比 Figure 7 Comparison between simulated and experimental weld pool shapes |
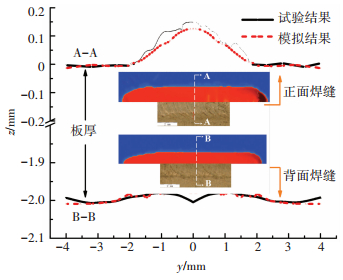
在图 8中,截取模拟时准稳态过程的焊缝,将其与实际焊缝熔宽作对比;利用超景深光学金相显微镜提取实际焊缝表面的轮廓线,将其与模拟焊缝表面轮廓线作对比,其中A-A、B-B截面对比结果见图 8曲线.可见,焊缝余高和下表面收缩轮廓线吻合较好,具体尺寸差异及相对误差如表 2所示.
|
图 8 模拟的焊缝形貌y与实际焊缝形貌对比 Figure 8 Comparison of simulated weld shape with actual weld joint morphology |
| 表 2 模拟结果与实验结果对比 Table 2 Comparison between simulated and experimental results |
由表 2可知,熔宽、余高和下表面收缩的误差都在一个合理的范围内,由此证明,本文对铝合金薄板穿透焊的温度场和流场的模拟是合理、正确的.
3 结论1) 对2 mm厚2219铝合金进行电子束穿透焊时,在Marangoni强对流的“拖拽”作用下,熔池上、下表面比熔池中间部分更长、更不稳定,形成了上、下两个熔池拖尾,熔池拖尾的长度在100 ms时达到稳定,熔池宽度在35 ms时达到稳定.
2) 在电子束焊接过程中,匙孔的形成不仅可以改变液态金属流速的大小,还可以改变流体流动的方向,在匙孔壁面上,液态金属在金属蒸汽反冲压力和Marangoni对流的作用下产生很大的流速,最大值可以达到10 m/s,使熔池剧烈震荡.
3) 金属蒸汽反作用力对熔池中流速的影响远远大于重力和表面张力的影响.
| [1] |
马正斌, 刘金合, 卢施宇, 等. 电子束焊接技术研究及进展[J].
电焊机, 2012, 42(4): 93-96.
MA Zhengbin, LIU Jinhe, LU Shiyu, et al. Research and development of electron beam welding[J]. Electric Welding Machine, 2012, 42(4): 93-96. DOI: 10.3969/j.issn.1001-2303.2012.04.022 |
| [2] |
周广德. 电子束焊接技术的特点和应用[J].
电工电能新技术, 1994, 4: 25-26.
ZHOU Guangde. Specialities and applications of electron beam welding[J]. Advanced Technology of Electrical Engineering and Energy, 1994, 4: 25-26. |
| [3] |
罗怡, 刘金合, 叶宏, 等. 镁合金真空电子束深熔焊接及焊缝成形数值模拟[J].
焊接学报, 2010, 31(6): 65-68.
LUO Yi, LIU Jinhe, YE Hong, et al. Numerical simulation on electron beam deep penetration welding and weld appearance of magnesium alloy[J]. Transactions of the China Welding Institution, 2010, 31(6): 65-68. |
| [4] |
霍宏伟. TIG焊三维熔池的数值模拟[D]. 兰州: 兰州理工大学, 2013.
HUO Hongwei. Numerical simulation of three-dimensional molten pool of TIG[D]. Lanzhou: Lanzhou University of Technology, 2013. |
| [5] |
CHO W I, NA S J, THOMY C, et al. Numerical simulation of molten pool dynamics in high power disk laser welding[J].
Journal of Materials Processing Technology, 2011, 212(1): 262-275.
DOI: 10.1016/j.jmatprotec.2011.09.011 |
| [6] |
ZHANG L J, ZHANG J X, GUMENYUK A, et al. Numerical simulation of full penetration laser welding of thick steel plate with high power high brightness laser[J].
Journal of Materials Processing Technology, 2014, 214(8): 1710-1720.
DOI: 10.1016/j.jmatprotec.2014.03.016 |
| [7] |
WU C S, ZHANG T, FENG Y H. Numerical analysis of the heat and fluid flow in a weld pool with a dynamic keyhole[J].
International Journal of Heat and Fluid Flow, 2013, 40: 186-197.
DOI: 10.1016/j.ijheatfluidflow.2013.01.006 |
| [8] |
DOWDEN J. The theory of laser material processing[M]. Berlin: Springer, 2009: 95-128.
|
| [9] |
SEMAK V, MATSUNAWA A. The role ofrecoil pressure in energy balance during laser materials processing[J].
Journal of PhysicsD Applied Physics, 1998, 30(18): 2541-2552.
DOI: 10.1088/0022-3727/30/18/008 |
| [10] |
吴甦, 赵海燕, 王煜, 等. 高能束焊接数值模拟中的新型热源模型[J].
焊接学报, 2004, 25(1): 91-94.
WU Su, ZHAO Haiyan, WANG Yu, et al. A new heat source model in numerical simulation of high energy beam welding[J]. Transactions of the China Welding Institution, 2004, 25(1): 91-94. |
| [11] |
傅献彩.
物理化学[M]. 第5版. 北京: 高等教育出版社, 2005: 122.
FU Xiancai. Physical chemistry[M]. 5th ed. Beijing: Higher Education Press, 2005: 122. |
| [12] |
LIU Chengcai, HE Jingshan. Numerical analysis offluid transport phenomena and spiking defect formation during vacuum electron beam welding of 2219 aluminum alloy plate[J].
Vacuum, 2016, 132: 73.
DOI: 10.1016/j.vacuum.2016.07.033 |
| [13] |
胡雪. 激光填粉焊接熔池流动数值模拟[D]. 哈尔滨: 哈尔滨工业大学, 2016.
HU Xue. Numerical simulation of weld pool flow in laser welding with powder feed[D]. Harbin: Harbin Institute of Technology, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10213-1016914630.htm |
 2017, Vol. 49
2017, Vol. 49


