连续相位调制(CPM)是一种非线性有记忆的频率调制方式,由于CPM信号相位连续, 所以该信号具有良好的频谱特性以及带外辐射小、旁瓣衰落快、瞬时包络恒定等优点,在抗非线性失真方面有良好的性能,因此,在卫星通信、机载舰载通信等民用和军用短波电台以及战术数据链中获得大量应用.
通常将调制系数为0.5的CPM信号称为MSK-Type调制.在MSK-Type的解调中,同步技术是各系统中迫切需要解决的技术难点. R. Melhan针对MSK调制提出MCM算法[1],但该算法只适用于MSK调制,对于采用其他成型滤波器的MSK-Type信号算法性能恶化严重,无法同步. Andrea在文献[2]中提出基于最大似然原理采用反馈结构的无数据辅助(NDA)算法,该算法利用劳伦特分解,将信号分解为线性PAM信号叠加的形式,再进行处理得到频偏信息.最初,此算法仅适用于MSK信号,后扩展到一般的CPM信号[3].文献[4]针对多进制和部分响应信号提出基于延迟相乘的频率同步算法,该方法采用前馈结构,频偏捕获范围可达到符号速率的150%,且适用范围广,复杂度低.但是牺牲了同步的精度,信号的自乘引入了大量的自噪声,其频偏估计的MSE曲线在信噪比为5 dB时达到10-3后便不随着信噪比的增加而衰减,所以算法同步性能很差.在文献[5]中,MENGALI和ANDREA对之前的同步算法进行了总结. M. Morelli在MCM算法的基础上进行改进[6],针对MSK-Type调制提出了载波频率和定时联合同步的算法,将原MCM算法在频率同步中的精度提高了多个数量级,且改进的MCM算法适用于GMSK信号.之后提出的一些频率同步算法包括国内学者在此方面的研究成果都存在着同步效率低或适用范围小等问题[7-10].所以寻找一种精度高,适用范围广的频率同步算法成为迫切需要.
在上述算法中,延迟相乘法易于实现且适用范围最广,基本涵盖所有的MSK-Type信号,所以本文从如何消除延迟相乘法中的自噪声入手,在已有的延迟相乘频率同步算法的基础上提出改进算法.改进算法在延迟相乘之前先对接收信号进行幂次非线性处理,这样可以将调制信息从信号中移除,仅留下频偏信息,进而消除了自噪声的影响.改进算法也解决了原算法因自噪声影响无法同步的问题,并将算法的精度提高了大约5个数量级.算法中需要对全响应与部分响应的信号进行不同的幂次处理,可以有效保证算法的精度和广适性.
1 MSK-Type信号模型接收信号r(t)由信号和噪声构成,具体表达式如下:
| $ r\left( t \right) = s\left( t \right) + {w_{\rm{R}}}\left( t \right) + {\rm{j}}{w_{\rm{I}}}\left( t \right) $ |
其中wR(t)和wI(t)为高斯白噪声的实部和虚部,两者相互独立,功率谱密度均定义为N0.发送信号s(t)的表达式为
| $ s\left( t \right) = \sqrt {\frac{{2{E_{\rm{s}}}}}{T}} {{\rm{e}}^{{\rm{j}}[\theta + \psi (\alpha ;{\rm{ }}t - \tau )]}} $ | (1) |
式(1)为MSK-Type的通用表达式,其中Es为每个符号的能量;T为符号周期;θ为载波相位;τ为定时误差. s(t)中ψ(α; t)为相位信息,具体表达式为
| $ \psi \left( {\alpha ;t} \right) = 2\pi h\sum\limits_i {{\alpha _i}q\left( {t - iT} \right)} . $ |
其中,α={αi}是码元序列.同时,假设码元符号独立且先验概率相等,取值在集合{±1, ±3, …, ±(M-1)}内,M为调制阶数, h为调制指数,对于MSK-Type信号而言,h恒为0.5;q(t)为相位脉冲,由频率脉冲g(t)积分得到,即
| $ q\left( t \right) = \left\{ {\begin{array}{*{20}{c}} {0,}\\ {1/2,} \end{array}\begin{array}{*{20}{l}} {t < 0;}\\ {t \ge LT.} \end{array}} \right. $ |
下面给出g(t)常用的几种脉冲形状的表达式:
LREC:
| $ g\left( t \right) = \left\{ {\begin{array}{*{20}{c}} {1/2LT,}&{0 \le t \le LT;}\\ {0,}&{其它.} \end{array}} \right. $ |
LRC:
| $ g\left( t \right) = \left\{ {\begin{array}{*{20}{c}} {\frac{1}{{2LT}}\left( {1 - {\rm{cos}}\frac{{2\pi t}}{{LT}}} \right),}&{0 \le t \le LT;}\\ {0,}&{其它.} \end{array}} \right. $ |
GMSK:
| $ g\left( t \right) = \frac{{Q\left( {2\pi B\left( {t - \frac{T}{2}} \right)} \right) - Q\left( {2\pi B\left( {t + \frac{T}{2}} \right)} \right)}}{{\sqrt {{\rm{ln}}2} }}. $ |
L=1且h=0.5的矩形脉冲对应的调制称为MSK调制;L>1或任一脉冲对应的调制称为MSK-Type调制.此外,将L=1时的信号称为全响应信号,将L>1的信号称为部分响应信号.本文只讨论g(t)是长度为L的矩形(LREC)和升余弦形(LRC)两种情况.此时q(t)=1/2-q(LT-t),满足几何对称的特性.
现假设处理信号的抗混叠滤波器为矩形,采样率为符号周期的N倍,抗混叠滤波器的带宽BAAF=N/2T.则信号经过抗混叠滤波器后进行采样得到
| $ x\left( k \right) = {{\rm{e}}^{j2\pi vk{T_{\rm{s}}}}}\sqrt {\frac{{2{E_{\rm{s}}}}}{T}} {{\rm{e}}^{{\rm{j}}\psi (\alpha ;k{T_{\rm{s}}} - \tau )}} + {n_{\rm{R}}}\left( k \right) + {\rm{j}}{n_{\rm{I}}}\left( k \right). $ | (2) |
由于之前的假设,{nR(k)}和{nI(k)}是独立的白随机数,它们的方差为σn2=N0/Ts.式(2)中的信号分量取决于α,θ和τ,只需要从N×L0个采样点中估计出频偏ν,便可以达到同步的目的,所以只要将其他两个参数的影响消去即可.
2 频率同步算法 2.1 延迟相乘法接收信号可由调制信和高斯白噪声构成:
| $ x(k{T_{\rm{s}}}) = s(k{T_{\rm{s}}}) + n(k{T_{\rm{s}}}). $ |
利用定时同步算法中自相关的思想,忽略噪声的影响,对接收信号进行延迟相乘得
| $ \begin{array}{l} z(k{T_{\rm{s}}}) = x(k{T_{\rm{s}}}){x^*}[\left( {k - D} \right){T_{\rm{s}}}] = \\ \quad \quad \frac{{2{E_{\rm{s}}}}}{T}{{\rm{e}}^{{\rm{j}}4\pi vD{T_s}}}{{\rm{e}}^{{\rm{j}}\{ \psi \left( {k{T_{\rm{s}}} - \tau ,\alpha } \right) - \psi (\left( {k - D} \right){T_{\rm{s}}} - \tau ,\alpha )\} }}, \end{array} $ |
其中D表示延迟的采样点数.对于数据符号取期望得到
| $ E\left\{ {z(k{T_{\rm{s}}})} \right\} = \frac{{2{E_{\rm{s}}}}}{T}A(k{T_{\rm{s}}}){{\rm{e}}^{{\rm{j}}2\pi vD{T_{\rm{s}}}}}. $ | (3) |
式中
| $ E\left\{ {\sum\limits_{k = 1}^{N{L_0}} {z(k{T_{\rm{s}}})} } \right\} = \frac{{2{E_{\rm{s}}}}}{T}N{L_0}\bar A{{\rm{e}}^{{\rm{j}}2\pi vD{T_{\rm{s}}}}}, $ |
式中
| $ {\hat v} = \frac{1}{{2\pi D{T_{\rm{s}}}}}\arg E\left\{ {\sum\limits_{k = 1}^{N{L_0}} {z(k{T_{\rm{s}}})} } \right\}. $ |
由于实际中期望不可获得,因此约等于
| $ \hat v = \frac{1}{{2\pi D{T_{\rm{s}}}}}\arg \left\{ {\sum\limits_{k = 1}^{N{L_0}} {z(k{T_{\rm{s}}})} } \right\}. $ | (4) |
延迟相乘算法框图如图 1所示.
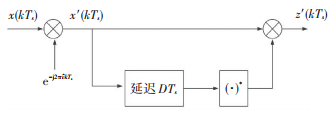
|
图 1 延迟相乘发算法框图 Figure 1 The block diagram of the delay-multiplication algorithm |
对信号进行延迟相乘可以消除信源和相位对频率估计的影响,但同时也引入了大量的自噪声,导致同步性能很差.不论是全响应信号还是部分响应信号频偏估计误差的方差与克拉美罗界相差甚远.所以为了消除自噪声,考虑将调制信息从信号中移除,只留下频偏信息.而通过对指数信号进行幂次处理可以将调制信息最终变为±π的整数倍,进而消除掉调制信息.本文采用先对信号进行幂次非线性处理,后进行延迟相乘的方式对信号进行同步.由于L参数的影响,需要根据L的不同而采取不同的非线性处理方式,以使得算法适用于部分相应信号.具体方法如下:
对于调制指数h=1/2和脉冲长度为L的MSK-Type信号,假设定时信息已经全部获得,采样率为符号速率,信号形式为
| $ s\left( {kT,\alpha } \right) = {{\rm{e}}^{{\rm{j}}[2\pi vkT + \theta ]}}\sqrt {\frac{{2{E_{\rm{s}}}}}{T}} {{\rm{e}}^{{\rm{j}}\psi (kT,\alpha )}}. $ |
先考虑全响应信号的情况,即脉冲长度L=1时,对信号进行平方非线性处理得到
| $ \begin{array}{l} z\left( {kT} \right) = {[x\left( {kT} \right){x^*}\left( {kT - T} \right)]^2} = \\ \quad \quad {\left( {\frac{{2{E_{\rm{s}}}}}{T}} \right)^2}{{\rm{e}}^{{\rm{j}}4\pi vT}}{{\rm{e}}^{{\rm{j}}2[\psi \left( {kT,\alpha } \right) - \psi (kT - T,\alpha )]}} \end{array} $ | (55) |
式中
| $ 2\left[ {\psi \left( {kT,\alpha } \right) - \psi \left( {kT - T,\alpha } \right)} \right] = 2\pi \sum\limits_i {{\alpha _i}p\left( {t - iT,T} \right)} . $ |
因为此时脉冲长度L=1,所以在一个码元周期内,相位增加了π/2,因此上式结果为
| $ 2\psi \left( {kT,\alpha } \right) - \psi \left( {kT - T,\alpha } \right) = \pm \pi , $ |
因此式(5)中最后一个指数项为-1,变为
| $ z\left( {kT} \right) = [x\left( {kT} \right){x^*}{\left( {kT - T} \right)]^2} = - {\left( {\frac{{2{E_{\rm{s}}}}}{T}} \right)^2}{{\rm{e}}^{{\rm{j}}4\pi vT}}. $ |
下面再考虑部分响应信号的情况,例如当脉冲长度L=2时,由于L的影响,要对信号进行2L也就是4次方非线性处理便可得到
| $ \begin{array}{l} z\left( {kT} \right) = {[x\left( {kT} \right){x^*}\left( {kT - T} \right)]^4} = \\ \quad \quad {\left( {\frac{{2{E_{\rm{s}}}}}{T}} \right)^4}{{\rm{e}}^{{\rm{j}}8\pi vT}}{{\rm{e}}^{{\rm{j}}4[\psi \left( {kT,\alpha } \right) - \psi (kT - T,\alpha )]}}. \end{array} $ | (6) |
因为此时在一个码元周期内,相位增加了±2π,所以得到
| $ 4\left[ {\psi \left( {kT,\alpha } \right) - \psi \left( {kT - T,\alpha } \right)} \right] = 0, $ |
因此式(5)中最后一个指数项为1,则式(6)可以写为
| $ z\left( {kT} \right) = {[x\left( {kT} \right){x^*}\left( {kT - T} \right)]^4} = {\left( {\frac{{2{E_{\rm{s}}}}}{T}} \right)^2}{{\rm{e}}^{{\rm{j}}4\pi vT}}. $ |
这样,综合公式(4)可得估计频偏的计算式为
| $ \hat v = \frac{1}{{4\pi T}}\arg \left\{ {{{\left( { - 1} \right)}^L} \times \sum\limits_{k = 0}^{{L_0} - 1} {z(kT)} } \right\}, $ |
其中
| $ z\left( {kT} \right) = [x\left( {kT} \right){x^*}{\left( {kT - T} \right)]^{2L}}. $ |
改进后的算法框图如图 2所示.
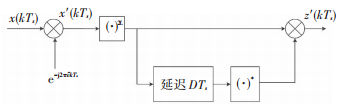
|
图 2 改进算法的原理框图 Figure 2 The block diagram of the improved algorithm |
由于该算法对信号实施了非线性变换处理,从算法推导中也可以看出,非线性处理弱化了噪声的影响,改进算法的同步性能更好.但由于非线性变换的存在该算法的频偏估计范围必然会减小,非线性次数越高,估计范围越小.
3 性能分析下面给出算法的性能分析,以及与现有算法的比较,频率估计的克拉美罗界为
| $ {\rm{MCRB}} = \frac{3}{{2{L_0}^3{\pi ^2}{T^2}}}{\left( {\frac{{{E_{\rm{s}}}}}{{{N_0}}}} \right)^{ - 1}}. $ |
所有仿真中观测长度均设为100个符号,蒙特卡罗循环为2 000次. 图 3和图 4分别针对多调制阶数和部分响应信号对延迟相乘法和改进算法进行了性能仿真,从图 3和图 4可以看出改进算法的精度比延迟相乘法高出很多.由于延迟相乘法的自噪声非常大,在信噪比5~30 dB范围内,频偏估计误差的MSE没有随着信噪比的增大而衰减,而改进算法随着信噪比的增加,均方误差曲线衰减且精度越来越高,在20dB时的精度比延迟相乘法提高了4个数量级,在25 dB时的精度比延迟相乘法提高了5个数量级.此外,从仿真中也可以看出改进算法也适用于部分响应的MSK-Type信号,进而证明了改进算法精度更高,涵盖范围更广.具体仿真结果如下.
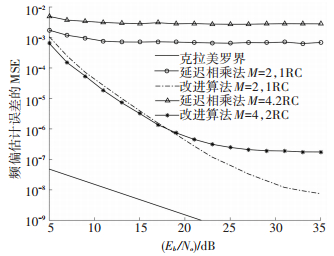
|
图 3 不同进制下频偏估计的方差与克拉美罗界对比 Figure 3 The frequency offset estimation variance compared with MCRB in different M |
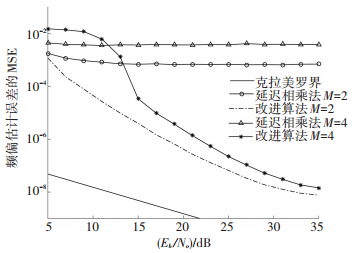
|
图 4 不同进制及不同脉冲长度下频偏估计的方差与克拉美罗界对比 Figure 4 The frequency offset estimation variance compared with MCRB in different M and L |
1) 仿真条件:进制数M=2、4;脉冲长度L=1;脉冲形状REC;归一化频偏vT为10%T(T为符号速率);过采样倍数N=4;抗混叠滤波器为8阶低通巴特沃斯滤波器,带宽Bw=0.75/T;Eb/N0=5~35 dB.
2) 仿真条件:进制数M=2,4;脉冲长度L=1,2,脉冲形状为RC;其余条件同上.
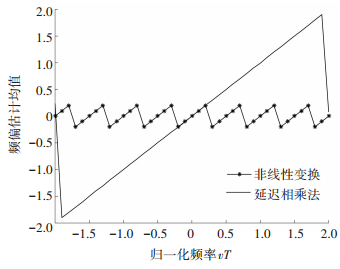
3.2 改进算法频偏捕获范围分析仿真条件:信噪比Eb/N0=20 dB,脉冲长度L=1,脉冲形状为REC,其余条件不变.频偏估计结果如图 5所示.
|
图 5 不同频偏下的估计范围对比 Figure 5 The comparison of estimation range under different frequency offsets |
在频偏捕获范围方面,改进算法的估计范围为符号速率的25%,而延迟相乘法的估计范围为180%.这是由于引入了幂次非线性变换,所以改进算法的频偏估计范围必然会减小,非线性次数越高,估计范围越小,仿真结果与理论一致.
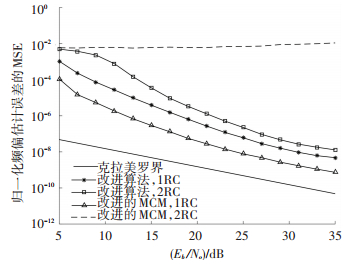
3.3 改进算法与改进的MCM算法比较现有的MSK-Type信号频率同步算法中比较成熟的是MCM算法和改进的MCM算法. MCM算法仅适用于MSK调制,而改进的MCM算法虽然适用于非矩形脉冲成形的MSK-Type信号,但是对于L>1的部分响应信号无法同步.针对这两种算法进行了比较.
从图 6可以看出,在L=1时即对MSK的同步中,改进的MCM算法同步性能优于本文的改进算法,但是当L=2时,即在部分响应信号中,改进的MCM算法同步性能急剧恶化,无法同步, 而本文的改进算法在信噪比为25dB时依旧可以衰减到10-8.进一步证明了本文提出的改进算法的广适性和良好的同步性能.
|
图 6 改进算法与改进的MCM算法的性能比较 Figure 6 The performance comparison of the improved algorithm and the improved MCM algorithm |
在MSK-Type信号的频率同步算法中,基于非线性的延迟相乘法在相乘过程中引入大量自噪声导致同步性能不佳,估计方差不随信噪比的增大而衰减,且曲线距离克拉美罗界较远.为了解决上述问题,本文在延迟相乘算法的基础上提出了改进算法.根据信号频率脉冲归一化长度L的不同采取不同的幂次非线性处理,将调制信息从信号中移除,仅剩下频偏信息.本算法消除了自噪声,解决了现有算法同步性能不佳的问题,将算法精度提高了约5个数量级.同时改进后的算法在部分响应和多进制信号的同步中性能依旧良好.
| [1] |
POLLOK A, MCkILLIAM R. Modified Cramér-Rao bounds for continuous-phase modulated signals[J].
IEEE Transactions on Communications, 2014, 62(5): 1681-1690.
DOI: 10.1109/TCOMM.2014.030814.130804 |
| [2] |
MEHLAN R, CHEN Y E, MEYR H. A fully digital feedforward MSK demodulator with joint frequency offset and symbol timing estimation for burst mode mobile radio[J].
IEEE Transactions on Vehicular Technology, 1993, 42(4): 434-443.
DOI: 10.1109/25.260769 |
| [3] |
D'Andrea A.N., GINESI A, MENGALI U. Frequency detectors for CPM signals[J].
IEEE Transactions on Communications, 1995, 43(2): 1828-1837.
|
| [4] |
D'Andrea A.N., GINESI A, MENGALI U.Digital carrier frequency estimation for multilevel CPM signals[C]// IEEE International Conference on Communications. Seattle: IEEE, 1995:1041-1045.
|
| [5] |
MENGALI U, D'Andrea A.N..
Synchronization techniques for digital receivers[M]. New York: Plenum Press, 1997.
|
| [6] |
MICHELE M, UNBERTO M. Joint frequency and timing recovery for MSK-type modulation[J].
IEEE Transactions on Communications, 1999, 47(6): 938-946.
DOI: 10.1109/26.771350 |
| [7] |
GUDOVSKIY D A, CHU L, LEE S. A novel non-data aided synchronization algorithm for MSK-type-modulated signals[J].
Communications Letters IEEE, 2015, 19: 1552-1555.
DOI: 10.1109/LCOMM.2015.2448535 |
| [8] |
刘毅. CPM信号载波同步研究[D]. 西安: 西安电子科技大学, 2008.
LIU Yi. Research on carrier synchronization of CPM signal[D]. Xi'an: Xi'an Electronic and Science University, 2008. http://cdmd.cnki.com.cn/article/cdmd-10701-2008055731.htm |
| [9] |
乔慧. 连续相位调制信号载波同步研究[D]. 西安: 西安电子科技大学, 2012.
QIAO Hui. Research on carrier synchronization of continuous phase modulated signal[D]. Xi'an: Xi'an Electronic and Science University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10701-1013114551.htm |
| [10] |
樊康敏. CPM收发机的关键技术研究[D]. 杭州: 浙江大学, 2015.
FAN Kangmin. Key technology research on CPM transceiver[D]. Hangzhou: Zhejiang University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10335-1015558711.htm |
 2017, Vol. 49
2017, Vol. 49


