卫星导航在高精度定位领域的应用越来越广泛，差分定位技术更是成为高精度定位的重要方法.单一频段的卫星导航信号由于观测量较少，使得其无论在整周模糊度的解算上还是在周跳的修复上，都存在可靠性和精度较低的问题.多频段的信号可增加观测量的冗余度，从而进一步提高卫星导航定位系统的可靠性和精度.随着北斗卫星导航系统的不断完善，北斗卫星导航系统可为用户提供B1/B2/B3共3个频点的高精度伪距和载波观测值.

以往的基于多频的研究主要集中在对多频组合系数的探讨^[1-3]和对周跳的探测、修复上^[4-6].对整周模糊度的多频解算大多都是基于Jung提出的CIR方法^[7]和Forssell等提出的TCAR方法^[8]：从宽巷测量值的整周模糊度比窄巷测量值的整周模糊度更容易解算的事实出发，通过多频观测值进行线性组合；从最宽巷组合到最窄巷组合逐级求出各组合的整周模糊度.但是CIR和TCAR方法都需要预先设定去相关矩阵，而且整周模糊度的解算成功率总是低于LAMBDA算法的解算成功率^[9-10].所以，本文提出一种新的基于LAMBDA算法的宽窄巷解算整周模糊度方法.在通过LAMBDA算法保证解算成功率的同时，充分利用宽巷解算整周模糊度的快速，以及窄巷载波相位测量误差小的特点，实现快速收敛和高精度的定位.

1 数学模型

本文采用华裔学者Chang Xiaowen所提的单差正交模型^[11-12]作为基线向量求解的基本模型，与双差模型不同的是其采用Householder变换削减钟差项$\beta _{{\rm{AB}}}^\varphi $，该方法不会使观测向量各个分量之间引入互相关，同时双差整周模糊度向量依然可获得.

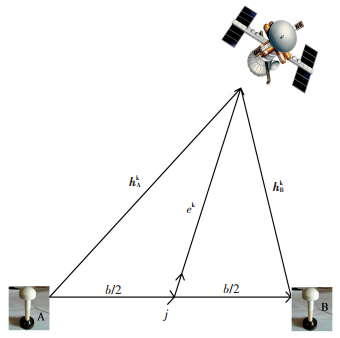
下图为高精度差分定位示意图.

基站为A，移动站为B，A的位置是由长时期的测绘得到的精确坐标，要得到B的准确位置，则需求出基线向量b.其关于卫星k在L_i波段的单差载波相位观测方程为

$ {\lambda _i}\left( {\varphi _{{\rm{i,AB}}}^{\rm{k}} + N_{{\rm{i,AB}}}^{\rm{k}}} \right) = r_{{\rm{AB}}}^{\rm{k}} + c\left( {\delta {t_{\rm{A}}} - \delta {t_{\rm{B}}}} \right) + v_{{\rm{i,AB}}}^{\rm{k}}. $

(1)

式中:$\varphi _{{\rm{i,AB}}}^{\rm{k}}$是A、B两个天线到卫星k的载波相位差分值的小数部分，N_{i, AB}^k是单差整周模糊度，r_AB^k是A、B间真实的距离单差值，λ_i是i波段的载波波长, δt_A和δt_B分别是2个接收机的接收机钟差，v_{i, AB}^k是接收机的单差载波相位观测噪声.

由r_AB^k=(‖h_A^k‖-‖h_B^k‖)，b=h_A^k-h_B^k，且‖2h_A^k-b‖e^k=2h_A^k-b=h_A^k+h_B^k，设变量矩阵E，可得

$ \mathit{\boldsymbol{E}} = {\left( {{\mathit{\boldsymbol{\omega }}^{\rm{k}}}{\mathit{\boldsymbol{e}}^{\rm{k}}}} \right)^{\rm{T}}} = \frac{{{{\left( {2\mathit{\boldsymbol{h}}_{\rm{A}}^{\rm{k}} - \mathit{\boldsymbol{b}}} \right)}^{\rm{T}}}}}{{\left\| {\mathit{\boldsymbol{h}}_{\rm{A}}^{\rm{k}}} \right\| + \left\| {\mathit{\boldsymbol{h}}_{\rm{A}}^{\rm{k}} - \mathit{\boldsymbol{b}}} \right\|}}, $

(2)

$ \mathit{\boldsymbol{E}} \cdot \mathit{\boldsymbol{b}} = r_{AB}^k. $

(3)

假设在L_i波段能观测到m_i颗卫星，则可把所有的单差载波相位观测值写成矩阵形式如下:

$ \mathit{\boldsymbol{y}}_{{\rm{i,s}}}^\varphi = \frac{1}{{{\lambda _i}}}\mathit{\boldsymbol{E}} \cdot \mathit{\boldsymbol{b}} - {\mathit{\boldsymbol{N}}_{{\rm{i,s}}}} + \mathit{\boldsymbol{e}}{\beta _{\rm{i}}} + \mathit{\boldsymbol{v}}_{{\rm{i,s}}}^\varphi ,\mathit{\boldsymbol{v}}_{{\rm{i,s}}}^\varphi \sim N\left( {0,2\sigma _{\varphi ,{\rm{i}}}^2{I_{{m_{\rm{i}}}}}} \right). $

(4)

式中：

$ \mathit{\boldsymbol{e}} = {\left( {1,1, \cdots ,1} \right)^{\rm{T}}},{\beta _{\rm{i}}} = c \cdot \left( {\delta {t_{\rm{A}}} - \delta {t_{\rm{B}}}} \right)/{\lambda _{\rm{i}}}, $

$ \mathit{\boldsymbol{y}}_{{\rm{i,s}}}^\varphi = \left[ {\begin{array}{*{20}{c}} {\varphi _{{\rm{i,AB}}}^1}\\ {\varphi _{{\rm{i,AB}}}^2}\\ \cdots \\ {\varphi _{{\rm{i,AB}}}^m} \end{array}} \right],{N_{{\rm{i,s}}}} = \left[ {\begin{array}{*{20}{c}} {N_{{\rm{i,AB}}}^1}\\ {N_{{\rm{i,AB}}}^2}\\ \cdots \\ {N_{{\rm{i,AB}}}^m} \end{array}} \right]. $

采用北斗的B1/B2/B3共3个频点进行组合，组合的系数分别设为k₁, k₂, k₃, 则

$ \varphi _{{\rm{AB}}}^{\rm{i}} = {k_1}\varphi _{{\rm{1,AB}}}^{\rm{i}} + {k_2}\varphi _{{\rm{2,AB}}}^{\rm{i}} + {k_3}\varphi _{{\rm{3,AB}}}^{\rm{i}}, $

(5)

$ N_{{\rm{AB}}}^{\rm{i}} = {k_1}N_{{\rm{1,AB}}}^{\rm{i}} + {k_2}N_{{\rm{2,AB}}}^{\rm{i}} + {k_3}N_{{\rm{3,AB}}}^{\rm{i}}, $

(6)

$ \lambda = \frac{1}{{\frac{{{k_1}}}{{{\lambda _1}}} + \frac{{{k_2}}}{{{\lambda _2}}} + \frac{{{k_3}}}{{{\lambda _3}}}}}, $

(7)

$ {\sigma _\varphi } = \sqrt {k_1^2 + k_2^2 + k_3^2} 2\alpha \lambda . $

(8)

其中α为以米为单位时，测量误差是波长的α倍.

通过将多频的载波观测量进行组合，可得

$ \mathit{\boldsymbol{y}}_{\rm{s}}^\varphi = \frac{1}{\lambda }\mathit{\boldsymbol{E}} \cdot \mathit{\boldsymbol{b}} - {\mathit{\boldsymbol{N}}_{\rm{s}}} + \mathit{\boldsymbol{e}}\beta + \mathit{\boldsymbol{v}}_{\rm{s}}^\varphi ,\mathit{\boldsymbol{v}}_{\rm{s}}^\varphi \sim N\left( {0,2\sigma _\varphi ^2{I_m}} \right). $

(9)

式中：$\mathit{\boldsymbol{y}}_{\rm{s}}^\varphi = \left[ {\begin{array}{*{20}{c}} {\varphi _{_{{\rm{AB}}}}^1}\\ {\varphi _{_{{\rm{AB}}}}^2}\\ \cdots \\ {\varphi _{_{{\rm{AB}}}}^{\rm{m}}} \end{array}} \right], {\mathit{\boldsymbol{N}}_{\rm{s}}} = \left[ {\begin{array}{*{20}{c}} {N_{AB}^1}\\ {N_{AB}^2}\\ \cdots \\ {N_{_{{\rm{AB}}}}^{\rm{m}}} \end{array}} \right]$，

$ \beta = c \cdot \left( {\delta {t_{\rm{A}}} - \delta {t_{\rm{B}}}} \right)/\lambda . $

采用Householder变换构造矩阵P∈R^m×m，使得$\mathit{\boldsymbol{P}}\; {\mathit{\boldsymbol{e}}_m} = \sqrt m \; {e_1}$，即构造

$ \mathit{\boldsymbol{P}} = {\mathit{\boldsymbol{I}}_{\rm{m}}} - \frac{{2\mathit{\boldsymbol{u}}\;{\mathit{\boldsymbol{u}}^{\rm{T}}}}}{{{\mathit{\boldsymbol{u}}^{\rm{T}}}\mathit{\boldsymbol{u}}}},\mathit{\boldsymbol{u}} \equiv {\mathit{\boldsymbol{e}}_1} - \frac{1}{{\sqrt m }}{\mathit{\boldsymbol{e}}_{\rm{m}}}. $

(10)

其中e₁=(1, 0, …, 0)^T=(1 0)^T，可得

$ \mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} {\frac{1}{{\sqrt m }}}&{\frac{{\mathit{\boldsymbol{\bar e}}_{{\rm{m}} - 1}^{\rm{T}}}}{{\sqrt m }}}\\ {\frac{{\mathit{\boldsymbol{\bar e}}_{{\rm{m}} - 1}^{\rm{T}}}}{{\sqrt m }}}&{{I_{{\rm{m}} - 1}} - \frac{{{{\mathit{\boldsymbol{\bar e}}}_{{\rm{m}} - 1}} \cdot \mathit{\boldsymbol{\bar e}}_{{\rm{m}} - 1}^{\rm{T}}}}{{m - \sqrt m }}} \end{array}} \right] \equiv \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{p}}_1}}\\ {\mathit{\boldsymbol{\bar P}}} \end{array}} \right]. $

(11)

其中$\mathit{\boldsymbol{\bar P}} = \left[ {\frac{{{{\mathit{\boldsymbol{\bar e}}}_{{\rm{m}} -1}}}}{{\sqrt m }}{\mathit{\boldsymbol{I}}_{{\rm{m}} -1}} -\frac{{{{\mathit{\boldsymbol{\bar e}}}_{{\rm{m}} -1}}\cdot{{\mathit{\boldsymbol{\bar e}}}_{{\rm{m}} -1}}^{\rm{T}}}}{{m -\sqrt m }}} \right], {{\mathit{\boldsymbol{\bar e}}}_{{\rm{m}} -1}} = {{\left({1, 1, \ldots, 1} \right)}^{\rm{T}}}$.将式(9)两边左乘P矩阵，即有

$ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{p}}_1}{\mathit{\boldsymbol{y}}^\varphi }}\\ {\mathit{\boldsymbol{\bar P}}{\mathit{\boldsymbol{y}}^\varphi }} \end{array}} \right] = \frac{1}{\lambda }\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{p}}_1}\mathit{\boldsymbol{E}}}\\ {\mathit{\boldsymbol{\bar PE}}} \end{array}} \right]\mathit{\boldsymbol{b}} - \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{p}}_1}{\mathit{\boldsymbol{N}}_{\rm{s}}}}\\ {\mathit{\boldsymbol{\bar P}}{\mathit{\boldsymbol{N}}_{\rm{s}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 1\\ \mathit{\pmb{0}} \end{array}} \right]\sqrt m \beta + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{p}}_1}\mathit{\boldsymbol{v}}_{\rm{s}}^\varphi }\\ {\mathit{\boldsymbol{\bar Pv}}_{\rm{s}}^\varphi } \end{array}} \right]. $

(12)

由式(12)可见，Householder变换之后有m-1个方程的钟差项系数都为0，或者说m-1个方程的钟差都转移到第一项里面，选择下面钟差项为0的m-1个方程，可得

$ \mathit{\boldsymbol{\bar P}}{\mathit{\boldsymbol{y}}^\varphi } = \frac{1}{\lambda }\mathit{\boldsymbol{\bar PEb}} - \mathit{\boldsymbol{\bar P}}{\mathit{\boldsymbol{N}}_{\rm{s}}} + \mathit{\boldsymbol{\bar Pv}}_{\rm{s}}^\varphi . $

(13)

由于Householder变换属于正交变换，其不改变噪声的统计特性，即有

$ \mathit{\boldsymbol{\bar Pv}}_{\rm{s}}^\varphi \sim N\left( {0,2\sigma _\varphi ^2{I_{{\rm{m}} - 1}}} \right). $

(14)

定义$\mathit{\boldsymbol{F}} \equiv {\mathit{\boldsymbol{I}}_{{\rm{m}} -1}} -\frac{{{{\mathit{\boldsymbol{\bar e}}}_{{\rm{m}} -1}}{{\mathit{\boldsymbol{\bar e}}}_{{\rm{m}} -1}}^{\rm{T}}}}{{m -\sqrt m }}, {\rm{ }}\mathit{\boldsymbol{J}} \equiv \left[ {\begin{array}{*{20}{c}} { -{{\mathit{\boldsymbol{\bar e}}}_{{\rm{m}} -1}}} & {{\mathit{\boldsymbol{I}}_{{\rm{m}} -1}}} \end{array}} \right]$，又由于双差整周模糊度定义为

${\mathit{\boldsymbol{N}}_D} = {\left[ {{N_{2, {\rm{s}}}} -{N_{1, {\rm{s}}}}, {N_{3, {\rm{s}}}} -{N_{1, {\rm{s}}}}, \ldots, {N_{{\rm{m}}, {\rm{s}}}} -{N_{1, {\rm{s}}}}} \right]^{\rm{T}}}$，则

$ \mathit{\boldsymbol{\bar P}}{\mathit{\boldsymbol{N}}_{\rm{s}}} = \mathit{\boldsymbol{FJ}}{\mathit{\boldsymbol{N}}_{\rm{s}}} = \mathit{\boldsymbol{F}}{\mathit{\boldsymbol{N}}_{\rm{D}}}. $

(15)

将式(15)代入式(13)当中，可得

$ \mathit{\boldsymbol{\bar P}}{\mathit{\boldsymbol{y}}^\varphi } = \frac{1}{\lambda }\mathit{\boldsymbol{\bar PEb}} - \mathit{\boldsymbol{F}}{\mathit{\boldsymbol{N}}_{\rm{D}}} + \mathit{\boldsymbol{\bar Pv}}_{\rm{s}}^\varphi ,\mathit{\boldsymbol{\bar Pv}}_{\rm{s}}^\varphi \sim N\left( {0,2\sigma _\varphi ^2{\mathit{\boldsymbol{I}}_{{\rm{m}} - 1}}} \right). $

(16)

令z=-N_D，记为双差整周模糊度.上式可表示为

$ \mathit{\boldsymbol{\bar P}}{\mathit{\boldsymbol{y}}^\varphi } = \frac{1}{\lambda }\mathit{\boldsymbol{\bar PEb}} + \mathit{\boldsymbol{Fz + \bar Pv}}_{\rm{s}}^\varphi ,\mathit{\boldsymbol{\bar Pv}}_{\rm{s}}^\varphi \sim \mathit{\boldsymbol{N}}\left( {0,2\sigma _\varphi ^2{\mathit{\boldsymbol{I}}_{{\rm{m}} - 1}}} \right). $

(17)

对$\frac{1}{\lambda }\mathit{\boldsymbol{\bar P}}E$进行QR分解，可得

$ {\mathit{\boldsymbol{Q}}^{\rm{T}}}\left( {\frac{1}{\lambda }\mathit{\boldsymbol{\bar PE}}} \right) = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{R}}\\ \mathit{\pmb{0}} \end{array}} \right]. $

(18)

式中:R是3×3维矩阵，Q是(m-1)×(m-1)维方阵，并且

$ {\mathit{\boldsymbol{Q}}^{\rm{T}}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{U}}\\ \mathit{\boldsymbol{V}} \end{array}} \right]. $

(19)

对式(17)左右两边同时乘以矩阵Q，可得方程

$ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{U\bar P}}{\mathit{\boldsymbol{y}}^\varphi }}\\ {\mathit{\boldsymbol{V\bar P}}{\mathit{\boldsymbol{y}}^\varphi }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{R}}\\ \mathit{\pmb{0}} \end{array}} \right]\mathit{\boldsymbol{b}} + \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{UFz}}}\\ {\mathit{\boldsymbol{VFz}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{U\bar Pv}}_{\rm{s}}^\varphi }\\ {\mathit{\boldsymbol{V\bar Pv}}_{\rm{s}}^\varphi } \end{array}} \right]. $

(20)

消去基线矢量b，可得方程

$ \mathit{\boldsymbol{V\bar P}}{\mathit{\boldsymbol{y}}^\varphi } = \mathit{\boldsymbol{VFz}} + \mathit{\boldsymbol{V\bar Pv}}_{\rm{s}}^\varphi ,\mathit{\boldsymbol{V\bar Pv}}_{\rm{s}}^\varphi \sim N\left( {0,2\sigma _\varphi ^2{\mathit{\boldsymbol{I}}_{{\rm{m}} - 4}}} \right). $

(21)

由于以上方程是亏秩的，而且单历元差分定位解算对接收机的测量精度有较高要求，所以本文采用多历元来解算整周模糊度的浮点解.即使采用低成本的接收机也可保证较高的差分定位精度.

式(21)是针对整周模糊度的求解，将得出的k个历元的方程联立，可得

$ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_1}\mathit{\boldsymbol{\bar Py}}_1^\varphi }\\ {{\mathit{\boldsymbol{V}}_2}\mathit{\boldsymbol{\bar Py}}_1^\varphi }\\ \vdots \\ {{\mathit{\boldsymbol{V}}_{\rm{k}}}\mathit{\boldsymbol{\bar Py}}_{\rm{k}}^\varphi } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_1}F}\\ {{\mathit{\boldsymbol{V}}_2}F}\\ \vdots \\ {{\mathit{\boldsymbol{V}}_{\rm{k}}}F} \end{array}} \right]\mathit{\boldsymbol{z}} + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_1}\mathit{\boldsymbol{\bar Pv}}_{\rm{s}}^\varphi }\\ {{\mathit{\boldsymbol{V}}_2}\mathit{\boldsymbol{\bar Pv}}_{\rm{s}}^\varphi }\\ \vdots \\ {{\mathit{\boldsymbol{V}}_{\rm{k}}}\mathit{\boldsymbol{\bar Pv}}_{\rm{s}}^\varphi } \end{array}} \right]. $

(22)

再对$\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_1}\mathit{\boldsymbol{F}}}\\ {{\mathit{\boldsymbol{V}}_2}\mathit{\boldsymbol{F}}}\\ \vdots \\ {{\mathit{\boldsymbol{V}}_{\rm{k}}}F} \end{array}} \right]$进行QR分解，可得

$ \mathit{\boldsymbol{T}}_{\rm{k}}^{\rm{T}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_1}\mathit{\boldsymbol{F}}}\\ {{\mathit{\boldsymbol{V}}_2}\mathit{\boldsymbol{F}}}\\ \vdots \\ {{\mathit{\boldsymbol{V}}_{\rm{k}}}F} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{S}}_k}}\\ \mathit{\pmb{0}} \end{array}} \right]. $

(23)

对方程左右两边同时乘以T_k^T，可得

$ \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat \omega }}}_{\rm{k}}}}\\ {{{\mathit{\boldsymbol{\bar \omega }}}_{\rm{k}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{S}}_k}}\\ \mathit{\pmb{0}} \end{array}} \right]\mathit{\boldsymbol{z + }}\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat v}}}_{\rm{k}}}}\\ {{{\mathit{\boldsymbol{\bar v}}}_{\rm{k}}}} \end{array}} \right]. $

(24)

由式(24)的上部分可得

$ {{\mathit{\boldsymbol{\hat \omega }}}_k} = {\mathit{\boldsymbol{S}}_k}\mathit{\boldsymbol{z}} + {{\mathit{\boldsymbol{\hat v}}}_k},{{\mathit{\boldsymbol{\hat v}}}_k} \sim N\left( {0,2\sigma _\varphi ^2{\mathit{\boldsymbol{I}}_{{\rm{m}} - 1}}} \right). $

(25)

此时，可得到整周模糊度的浮点解，通过LAMBDA算法对浮点解进行解算可得到初始时刻的整周模糊度z. LAMBDA算法能够按照固定解与浮点解的残差由小到大依次给出多个候选值，排列次序代表着候选值的“最佳程度”，第一个候选值是最优的，第二个候选值是次优的.如果浮点解精度足够高，那么第一个候选值就是真实的整周模糊度，如果浮点解精度不够高，那么真实解的位置很可能不是第一个，这个时候固定得到的整周模糊度的整数解就不是准确的.所以通过多历元的联立求解，增加观测量的冗余度可提高浮点解的精度，从而通过LAMBDA算法解算出真实的整周模糊度.而宽巷组合的载波观测量因为其长波长的特性，本身的整周模糊度浮点解精度就较高，所以联立相对较少的历元就可得到精度足够高的浮点解，从而在较短的收敛时间下，解算出准确的整周模糊度^[13].

先分别通过3组不同的宽巷系数固定得到3组不同的宽巷整周模糊度，再进行窄巷组合的整周模糊度求解.根据前3个宽巷整周模糊度求解出用于约束窄巷整周模糊度的整周模糊度.即

$ {\mathit{\boldsymbol{z}}_{{\rm{WL1}}}} = {k_1}{\mathit{\boldsymbol{z}}_1} + {k_2}{\mathit{\boldsymbol{z}}_2} + {k_3}{\mathit{\boldsymbol{z}}_3}, $

(26a)

$ {\mathit{\boldsymbol{z}}_{{\rm{WL2}}}} = {{k'}_1}{\mathit{\boldsymbol{z}}_1} + {{k'}_2}{\mathit{\boldsymbol{z}}_2} + {{k'}_3}{\mathit{\boldsymbol{z}}_3}, $

(26b)

$ {\mathit{\boldsymbol{z}}_{{\rm{WL3}}}} = {{k''}_1}{\mathit{\boldsymbol{z}}_1} + {{k''}_2}{\mathit{\boldsymbol{z}}_2} + {{k''}_3}{\mathit{\boldsymbol{z}}_3}. $

(26c)

分别求出z₁, z₂, z₃，从而得到约束窄巷整周模糊度的整周模糊度

$ {{\mathit{\boldsymbol{z'}}}_{{\rm{NL}}}} = {{k''}_1}{\mathit{\boldsymbol{z}}_1} + {{k''}_2}{\mathit{\boldsymbol{z}}_2} + {{k''}_3}{\mathit{\boldsymbol{z}}_3}. $

(27)

同时窄巷组合建模后依旧进行自身整周模糊度的解算.即

$ \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat \omega }}}_{{\rm{k,NL}}}}}\\ {{{\mathit{\boldsymbol{\bar \omega }}}_{{\rm{k,NL}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{S}}_{{\rm{k,NL}}}}}\\ 0 \end{array}} \right]{\mathit{\boldsymbol{z}}_{{\rm{NL}}}} + \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat v}}}_{{\rm{k,NL}}}}}\\ {{{\mathit{\boldsymbol{\bar v}}}_{{\rm{k,NL}}}}} \end{array}} \right], $

(28a)

$ {{\mathit{\boldsymbol{\hat \omega }}}_{\rm{k}}} = {\mathit{\boldsymbol{S}}_k}\mathit{\boldsymbol{z}} + {{\mathit{\boldsymbol{\hat v}}}_{\rm{k}}},{{\mathit{\boldsymbol{\hat v}}}_{\rm{k}}} \sim N\left( {0,2\sigma _{\varphi ,{\rm{NL}}}^2{\mathit{\boldsymbol{I}}_{{\rm{m}} - 1}}} \right). $

(28b)

窄巷组合的组合波长短，解算出准确的整周模糊度比较难，需要经过多个历元的不断收敛才能得到准确的整周模糊度，相对于宽巷组合定位而言收敛时间较长.本文利用宽巷组合求解出的窄巷整周模糊度进行约束，从而保证定位解算时整周模糊度的收敛时间较短.

一旦|z_NL-z_NL^′|≥T_threshold，则取通过宽巷整周模糊度求解出来的窄巷整周模糊度作为整周模糊度的解算结果，否则采用窄巷组合自身得到的整周模糊度进行定位解算.根据式(20)可得到基线向量解算结果

$ {\mathit{\boldsymbol{U}}_{{\rm{NL}}}}{{\mathit{\boldsymbol{\bar P}}}_{{\rm{NL}}}}\mathit{\boldsymbol{y}}_{{\rm{NL}}}^\varphi = {\mathit{\boldsymbol{R}}_{{\rm{NL}}}}\mathit{\boldsymbol{b}} + {\mathit{\boldsymbol{U}}_{{\rm{NL}}}}{\mathit{\boldsymbol{F}}_{{\rm{NL}}}}{\mathit{\boldsymbol{z}}_{{\rm{NL}}}} + {\mathit{\boldsymbol{U}}_{{\rm{NL}}}}{{\mathit{\boldsymbol{\bar P}}}_{{\rm{NL}}}}\mathit{\boldsymbol{v}}_{{\rm{NL,s}}}^\varphi . $

(29)

其中基线解算噪声的统计量为

$ {\mathit{\boldsymbol{U}}_{{\rm{NL}}}}{{\mathit{\boldsymbol{\bar P}}}_{{\rm{NL}}}}\mathit{\boldsymbol{v}}_{{\rm{NL,s}}}^\varphi \sim N\left( {0,2\sigma _{\varphi ,{\rm{NL}}}^2{\mathit{\boldsymbol{I}}_3}} \right). $

(30)

因为窄巷整周模糊度z_NL已知，可求得基线向量b.此时的误差U_NLP_NL$\mathit{\boldsymbol{v}}_{{\rm{NL, s}}}^\varphi $ 是基于窄巷组合的载波组合观测误差，根据式(8)可知，

$ {\sigma _{\varphi ,{\rm{NL}}}} < {\sigma _\varphi } < {\sigma _{\varphi ,{\rm{WL}}}}. $

窄巷组合具有较低的组合观测误差，所以基线向量定位解算时误差噪声较小，解算出的基线向量精度较高.

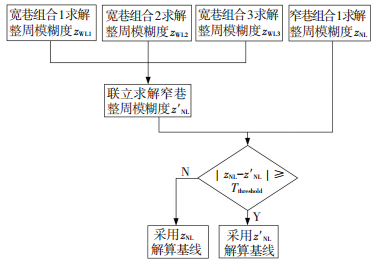
宽窄巷方法结合的具体流程图见图 2.单纯的采用宽巷组合的方法进行定位解算，虽然能较快地固定出正确的整周模糊度，但是在宽巷化的过程中增加了载波组合的观测噪声，会对定位精度造成影响.单纯的采用窄巷组合的方法进行定位解算，虽然组合后的观测噪声较低，有利于提高定位精度，但是窄巷组合不利于整周模糊度的快速固定，会延长定位的收敛时间.而本文提出的方法，在充分利用宽巷组合定位收敛时间短优势的同时，进一步利用窄巷组合的低噪声特点提高定位精度.从而实现收敛时间较短，定位精度高的基线解算结果.

2 实验验证

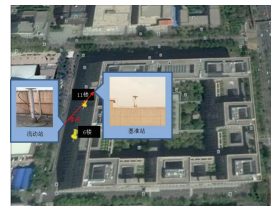
为验证算法的可行性，对系统进行短基线测试.短基线测试的地点选择在北京市北京航空航天大学新主楼F座楼顶，测试时长19 753个历元(约为5.5 h).基准站和监测站间相距约23 m.控制中心运行在电脑上，通过网线进行基准站、监测站和控制中心的数据传输.监测站、基准站和控制中心的电脑均通过LAN连接到交换机.监测站和基准站均采用的是北斗星通BDM 610的板卡，支持GPS L1/L2和BD B1/B2/B3共5个频点，可设置为五频输出.测试的实际场地见图 3.

北斗3个频点B1/B2/B3的波长分别为19 cm，24 cm，23 cm.对于短基线, 电离层和对流层通过双差几乎完全消除.在这种情形下, 主要误差源是观测噪声和多路径误差.所选组合应具有较小的噪声放大因子和较长的波长，(1, -1, 0)和(1, 0, -1)噪声放大因子相对较小, 是较为合理的选择.同时, 原始观测值(1, 0, 0), (0, 1, 0)或(0, 0, 1)具有最小的噪声放大因子，虽然波长较短，但是选择其中一个可有效的进行宽巷3个整周模糊度的联立求窄巷整周模糊度.所以，本文选取

$ \begin{array}{l} {k_1} = 1,{k_2} = 0,{k_3} = - 1;{{k'}_1} = 1,{{k'}_2} = - 1,{{k'}_3} = 0;\\ {{k''}_1} = 0,{{k''}_2} = 0,{{k''}_3} = 1;{{k'''}_1} = 0,{{k'''}_2} = 1,{{k'''}_3} = 1 \end{array} $

则：

$ {\lambda _{{\rm{WL1}}}} = 1.03,{\lambda _{{\rm{WL2}}}} = 0.85,{\lambda _{{\rm{WL3}}}} = 0.23,{\lambda _{{\rm{NL}}}} = 0.12. $

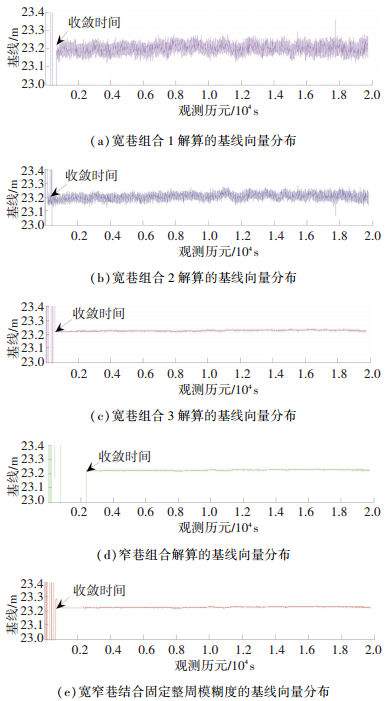
考虑到3个宽巷组合的整周模糊度联立求解窄巷整周模糊度的过程中会出现小数部分的取舍，所以设置宽巷求解的整周模糊度约束窄巷自身求解的整周模糊度的阈值为T_threshold=3(cycle), 结果见图 4.

根据图 4和表 1可见，宽巷组合载波测量值较易于整周模糊度的解算，相应的在基线求解时收敛时间短.但是宽巷化会放大测量噪声，使解算结果含有的误差较大.而窄巷组合载波测量值较不利于整周模糊度的解算，相应的在基线求解时候收敛时间较长，但是通过窄巷化可减小测量噪声，提高解算精度.本文提出的方法，通过宽巷组合联立得到的窄巷整周模糊度约束窄巷组合自身求得的整周模糊度，可既保留宽巷整周模糊度易于解算的优势，解算收敛时间相对较短，又可保证整周模糊度固定后的测量噪声较小，实现高精度的定位解算.

3 结论

本文提出一种宽窄巷组合进行LAMBDA整周模糊度解算的方式，通过LAMBDA算法求得的3组宽巷整周模糊度的联立得到窄巷系数组合下的整周模糊度，进一步约束窄巷组合自身通过LAMBDA算法求得的窄巷整周模糊度.有效的利用北斗三频点的组合信息，吸收宽巷化和窄巷化的优点得到收敛时间较短，定位精度高的基线解算结果.为验证算法的可用性，本文采用实际接收的北斗三频信号进行实验，宽窄巷组合后的静态定位精度为3 mm，收敛时间大约为12 min.与收敛时间短的宽巷组合相比，在收敛时间基本相同的情况下，本文的方法在定位精度上相较于宽巷组合定位结果的厘米级误差有明显的改善，实现毫米级的定位精度；与精度同样在3mm的窄巷组合定位结果相比，本文的方法明显缩短收敛时间，收敛时间缩短一半以上.