质量管理学家朱兰曾指出“21世纪将是质量的世纪”,产品质量不仅是企业的生命线,更是在全球市场上赢得顾客的关键.如何通过改进质量工程技术,来提高产品质量、竞争优势,已成为国内外工业界和学术界极为关注的问题.质量专家田口玄一博士将数理统计、经济学运用到质量工程中,形成离线质量控制和在线质量控制理论,创立质量工程学并提出三次设计(系统设计、参数设计、容差设计)的质量工程方法[1].
参数设计是离线质量控制的核心,是以试验设计为基础,通过结合统计知识和工程技术而发展起来的一种质量改进方法.其基本原理为选择最佳的参数组合以达到产品过程对不确定因素的变化不敏感,从而提高产品过程的稳健性,使产品性能更加稳定可靠[2].统计学家Box和Wilson首先提出响应曲面方法,之后Shoemaker等引入到参数设计中[3].该方法首先通过试验设计建立设计变量与质量特性之间的响应曲面模型,并优化所构建的目标函数,从而确定最佳的因子水平组合. Vining等[4]指出质量特性对目标值的波动是由均值偏差和方差组成,需要同时考虑均值波动和方差波动对结果的影响,因此提出了双响应曲面方法.响应曲面法具有推导严谨和模型可靠的优点,被广泛地用于产品过程的参数设计研究和实践[5-7].
容差设计通常是在系统设计和参数设计确定了设计变量的最佳水平组合后,通过研究容差范围与质量成本之间的关系,根据各设计变量波动对产品质量特性影响的大小,从经济性角度考虑是否需要对设计变量的容差进行调整.近年来,有不少学者关注于产品过程的容差设计问题. Jin等[8]基于非对称质量损失函数,对服从非正态分布的产品容差设计进行了研究. Zhao等[9]根据产品服务的寿命分布,从质量损失和制造成本的角度构建服务的现值模型,进而提出基于服务质量损失的最优容差经济设计方法. Zhang等[10]考虑了质量特性类型的不同,采用质量损失函数法解决递阶产品的容差经济性设计问题.另外,Peng等[11-13]也分别针对不同问题提出了相应的容差设计方法.以上研究都是在预先设定的模型和最优设计变量情况下单独对设计变量的容差进行设计,然而有学者指出同时考虑参数设计和容差设计问题,有助于提高产品过程的经济性和可靠性[14]. Kim等[15]采用双响应曲面的方法构建响应均值和方差的模型,同时考虑田口质量损失成本和容差成本,对参数与容差进行经济性设计. Jeang等[16]从质量和成本的角度,同时对设计容差、过程均值和过程容差进行并行优化设计. He等[17]在优化过程中引入了Cp过程能力指数,进而对参数与容差经济性设计进行改进.张志红等[18]考虑到噪声变量对响应曲面建模的影响,以过程方差置信域为约束,提出考虑噪声变量的参数和容差经济性设计策略.这些研究忽视了两方面的问题:一方面,响应曲面模型是一个近似的替代模型,拟合过程中存在模型参数不确定性的问题;另一方面,质量损失函数系数通常是依据经验而主观设定,若系数设定不当,会对优化结果产生较坏影响.
本文针对产品系统的参数和容差设计的问题,从质量损失成本和容差成本的角度,提出了基于置信水平和熵权法的参数和容差经济性设计方法.该方法一方面通过最大化置信水平的方式,尽可能减少模型参数不确定性对最优设计变量的影响;另一方面充分利用客观信息,采用熵权法计算质量损失函数系数,避免主观假定系数值导致的最优容差不合理的问题.
1 质量损失函数田口认为“质量特性一旦偏离其设计目标值,就会造成质量损失,偏离越远,损失越大”,并指出产品过程的质量损失与它的均方差大约成正比关系.为了近似地描述产品质量特性y偏离目标值造成的质量损失,田口提出了二次损失函数[2].
| $ L\left[ {y\left( \mathit{\boldsymbol{x}} \right)} \right] = w{\left[ {y\left( \mathit{\boldsymbol{x}} \right) - T} \right]^2}. $ | (1) |
式中:x为设计变量的向量,T为质量特性的目标值,w为可以将质量特性偏差转化为方便比较的价值单位的函数系数,通常由功能界限和丧失功能的损失来确定.为了进一步量化质量损失,田口又提出了期望损失函数.
| $ \begin{array}{*{20}{c}} {E\left\{ {L\left[ {y\left( \mathit{\boldsymbol{x}} \right)} \right]} \right\} = wE{{\left[ {y\left( \mathit{\boldsymbol{x}} \right) - T} \right]}^2} = w\left\{ {{\sigma ^2}\left( \mathit{\boldsymbol{x}} \right) + } \right.}\\ {\left. {{{\left[ {\mu \left( \mathit{\boldsymbol{x}} \right) - T} \right]}^2}} \right\}.} \end{array} $ | (2) |
显然,为了减小产品过程的质量损失,应使质量特性的均值达到或接近设计目标值的情况下,尽可能地减少质量特性的波动.需要注意的是,该质量损失函数是用于计算望目质量特性的质量损失.根据田口的质量观,质量特性被分为望目特性、望小特性和望大特性三种类型.对于望小特性和望大特性,可以采用以下质量损失函数进行计算[10].
若质量特性y为望小特性时,那么其目标值可设为0,其质量损失函数为
| $ L\left[ {y\left( \mathit{\boldsymbol{x}} \right)} \right] = w{y^2}\left( \mathit{\boldsymbol{x}} \right). $ | (3) |
故而可以得到其期望质量损失函数为
| $ E\left\{ {L\left[ {y\left( \mathit{\boldsymbol{x}} \right)} \right]} \right\} = wE\left[ {{y^2}\left( \mathit{\boldsymbol{x}} \right)} \right] = w\left[ {{\sigma ^2}\left( \mathit{\boldsymbol{x}} \right) + {\mu ^2}\left( \mathit{\boldsymbol{x}} \right)} \right]. $ | (4) |
类似地,当质量特性y为望大特性时,1/y即为望小质量特性,其质量损失函数为
| $ L\left[ {y\left( \mathit{\boldsymbol{x}} \right)} \right] = \frac{w}{{{y^2}\left( \mathit{\boldsymbol{x}} \right)}}. $ | (5) |
通过泰勒级数展开,可以得到其近似期望质量损失函数为
| $ E\left\{ {L\left[ {y\left( \mathit{\boldsymbol{x}} \right)} \right]} \right\} = wE\left[ {\frac{1}{{{y^2}\left( \mathit{\boldsymbol{x}} \right)}}} \right] = \frac{w}{{{\mu ^2}\left( \mathit{\boldsymbol{x}} \right)}}\left[ {1 + \frac{{3{\sigma ^2}\left( \mathit{\boldsymbol{x}} \right)}}{{{\mu ^2}\left( \mathit{\boldsymbol{x}} \right)}}} \right]. $ | (6) |
通过以上质量损失函数,依据质量特性的不同可以计算质量损失成本.
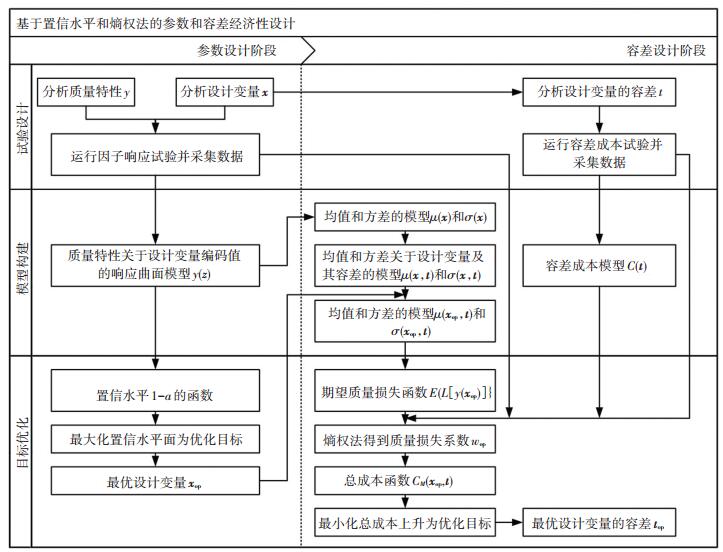
2 本文方法本文考虑到模型参数不确定性和质量损失函数系数对优化结果的影响,运用置信水平方法和熵权方法,对产品系统的参数和容差进行经济性设计. 图 1为本文方法流程图,由流程图可以看出:该方法分为参数设计和容差设计两个阶段,每个阶段又分为“试验设计-模型构建-目标优化”三个步骤.具体的流程步骤如下.
|
图 1 本文方法的流程步骤图 Figure 1 The flow chart of the proposed approach |
步骤一 因子响应试验设计.分析案例,确定产品过程的质量特性和设计变量.根据试验中的设计变量和约束条件的情况,结合制造商和顾客对产品生产的安全性和经济性要求,选择合适的因子响应试验设计方法.运行试验并收集相关的试验数据.
步骤二 响应曲面模型构建.根据步骤一获得的因子响应试验数据,拟合质量特性y的响应曲面模型.
假设y表示产品系统的质量特性,zi(i=1, 2, …m)表示第i个设计变量,则质量特性y的二阶模型如下所示:
| $ y\left( \mathit{\boldsymbol{z}} \right) = {\beta _0} + \sum\limits_{i = 1}^m {{\beta _i}{z_i}} + \sum\limits_{i = 1}^m {{\beta _{ii}}z_i^2} + \sum\limits_{i = j}^m {\sum\limits_{i < j}^m {{\beta _{ij}}{z_i}{z_j} + \varepsilon } } . $ | (7) |
式中:z=(z1, z2…zm),β0、βi和βij分别表示模型的常数项、一次项和二次项的回归系数,ε为拟合误差且服从正态分布N(0, σε2).采用最小二乘回归法拟合得到y的响应曲面模型函数
| $ \hat y\left( \mathit{\boldsymbol{z}} \right) = {{\hat \beta }_0} + \sum\limits_{i = 1}^m {{{\hat \beta }_i}{z_i}} + \sum\limits_{i = 1}^m {{{\hat \beta }_{ii}}z_i^2} + \sum\limits_{i = j}^m {\sum\limits_{i < j}^m {{{\hat \beta }_{ij}}{z_i}{z_j}} } . $ | (8) |
式中
步骤三 参数设计的目标优化.由步骤二中质量特性y的响应曲面估计模型,分析模型系数所服从的数学分布情况.再依据质量特性的类型,得到质量特性置信水平的计算公式.通过最大化y的置信水平,得到最优设计变量的水平组合.
1) 质量特性y置信水平的计算
关于质量特性y,通过对设计变量进行显著性检验,筛选出显著性变量,得到模型显著性变量的向量
| $ \mathit{\boldsymbol{Z}} = {\left( {1, \cdots ,{z_v}, \cdots z_w^2, \cdots ,{z_e}{z_f}, \cdots } \right)^{\rm{T}}}. $ | (9) |
可得模型系数的向量
| $ \mathit{\boldsymbol{\hat \beta }} = {\left( {{{\hat \beta }_0}, \cdots ,{{\hat \beta }_v}, \cdots {{\hat \beta }_{ww}}, \cdots ,{{\hat \beta }_{ef}}, \cdots } \right)^{\rm{T}}}. $ | (10) |
那么,式(8)可写成
| $ \hat y\left( \mathit{\boldsymbol{z}} \right) = {Z^{\rm{T}}}\mathit{\boldsymbol{\hat \beta }}. $ | (11) |
假设zip(p=1, 2, …P)为设计变量zi在第p组实验时的样本数据,可得样本数据矩阵
| $ \mathit{\boldsymbol{X = }}\left[ {\begin{array}{*{20}{c}} 1& \cdots &{{z_{v1}}}& \cdots &{z_{w1}^2}& \cdots &{{z_{e1}}{z_{f1}}}& \cdots \\ 1& \cdots &{{z_{v2}}}& \cdots &{z_{w2}^2}& \cdots &{{z_{e2}}{z_{f2}}}& \cdots \\ \vdots &{}&{}& \ddots &{}&{}&{}& \vdots \\ 1& \cdots &{{z_{vP}}}& \cdots &{z_{wP}^2}& \cdots &{{z_{eP}}{z_{fP}}}& \cdots \end{array}} \right]. $ | (12) |
采用均方误差方法来估计响应曲面模型随机误差的方差σε2,可得其估计值
| $ \begin{array}{l} \hat \sigma _\varepsilon ^2 = \frac{1}{{P - b}}\left( {\hat \varepsilon _1^2 + \hat \varepsilon _2^2 + \cdots + \hat \varepsilon _t^2 + \cdots + \hat \varepsilon _n^2} \right) = \\ \;\;\;\;\;\;\;\;\frac{1}{{P - b}}\sum\limits_{p = 1}^P {{{\left[ {{y_p}\left( \mathit{\boldsymbol{z}} \right) - {{\hat y}_p}\left( \mathit{\boldsymbol{z}} \right)} \right]}^2}} . \end{array} $ | (13) |
式中: b为均值模型中需要估计的模型系数个数;
Montergomery指出:由于最小二乘估计值
| $ \frac{{{{\hat \beta }_i} - {\beta _i}}}{{\sqrt {\hat \sigma _\varepsilon ^2{\mathit{\boldsymbol{X}}_{ii}}} }},i = 0,1, \cdots ,m $ |
服从自由度为P-b的t分布,其中Xjj是矩阵(XTX)-1第(jj)个元素.因此,当置信水平为1-α时模型系数
| $ \left[ {{\beta _{{\rm{L}};i}},{\beta _{{\rm{U}};i}}} \right] = \left[ {{{\hat \beta }_i} - {t_{\alpha /2,n - p}}\sqrt {\hat \sigma _\varepsilon ^2{\mathit{\boldsymbol{X}}_{ii}}} ,{{\hat \beta }_i} + {t_{\alpha /2,n - p}}\sqrt {\hat \sigma _\varepsilon ^2{\mathit{\boldsymbol{X}}_{ii}}} } \right]. $ | (14) |
因此,质量特性估计值的误差方差计算公式为
| $ Se\left\{ {\hat y\left( \mathit{\boldsymbol{z}} \right)} \right\} = \hat \sigma _\varepsilon ^2{\mathit{\boldsymbol{Z}}^{\rm{T}}}{\left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}}} \right)^{ - 1}}\mathit{\boldsymbol{Z}}. $ | (15) |
当置信水平为1-α时,质量特性y的双侧置信区间为
| $ \begin{array}{*{20}{c}} {\left[ {{y_{\rm{L}}}\left( \mathit{\boldsymbol{z}} \right),{y_{\rm{U}}}\left( \mathit{\boldsymbol{z}} \right)} \right] = \left[ {\hat y\left( \mathit{\boldsymbol{z}} \right) - {t_{\alpha /2,n - p}}\sqrt {\hat \sigma _\varepsilon ^2{\mathit{\boldsymbol{Z}}^{\rm{T}}}{{\left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}}} \right)}^{ - 1}}\mathit{\boldsymbol{Z}}} ,} \right.}\\ {\left. {\hat y\left( \mathit{\boldsymbol{z}} \right) + {t_{\alpha /2,n - p}}\sqrt {\hat \sigma _\varepsilon ^2{\mathit{\boldsymbol{Z}}^{\rm{T}}}{{\left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}}} \right)}^{ - 1}}\mathit{\boldsymbol{Z}}} } \right].} \end{array} $ | (16) |
式中:tα/2, n-p表示显著性水平和自由度分别为α/2和P-b时的t分布分位数,P为试验的次数.因此质量特性y的单侧置信区间为
| $ \left[ {{y_{\rm{L}}}\left( \mathit{\boldsymbol{z}} \right), + \infty } \right] = \left[ {\hat y\left( \mathit{\boldsymbol{z}} \right) - {t_{\alpha /2,n - p}}\sqrt {\hat \sigma _\varepsilon ^2{\mathit{\boldsymbol{Z}}^{\rm{T}}}{{\left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}}} \right)}^{ - 1}}\mathit{\boldsymbol{Z}}} , + \infty } \right], $ | (17) |
| $ \left[ { - \infty ,{y_{\rm{U}}}\left( \mathit{\boldsymbol{z}} \right)} \right] = \left[ { - \infty ,\hat y\left( \mathit{\boldsymbol{z}} \right) + {t_{\alpha /2,n - p}}\sqrt {\hat \sigma _\varepsilon ^2{\mathit{\boldsymbol{Z}}^{\rm{T}}}{{\left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}}} \right)}^{ - 1}}\mathit{\boldsymbol{Z}}} } \right]. $ | (18) |
由此可得如下质量特性y置信水平的计算公式:
当y为望目质量特性时
| $ \begin{array}{l} 1 - \alpha = pro\left\{ {\hat y - {t_{\alpha /2,n - p}}\sqrt {\hat \sigma _\varepsilon ^2{\mathit{\boldsymbol{Z}}^{\rm{T}}}{{\left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}}} \right)}^{ - 1}}\mathit{\boldsymbol{Z}}} \le y} \right.\\ \;\;\;\;\left. { \le \hat y + {t_{\alpha /2,n - p}}\sqrt {\hat \sigma _\varepsilon ^2{\mathit{\boldsymbol{Z}}^{\rm{T}}}{{\left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}}} \right)}^{ - 1}}\mathit{\boldsymbol{Z}}} } \right\}. \end{array} $ | (19) |
当y为望小质量特性时
| $ \begin{array}{l} 1 - \alpha = pro\left\{ {y\left( \mathit{\boldsymbol{z}} \right) \le \hat y\left( \mathit{\boldsymbol{z}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {{t_{\alpha /2,n - p}}\sqrt {\hat \sigma _\varepsilon ^2{\mathit{\boldsymbol{Z}}^{\rm{T}}}{{\left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}}} \right)}^{ - 1}}\mathit{\boldsymbol{Z}}} } \right\}. \end{array} $ | (20) |
当y为望大质量特性时
| $ 1 - \alpha = pro\left\{ {y\left( \mathit{\boldsymbol{z}} \right) \ge \hat y\left( \mathit{\boldsymbol{z}} \right) - {t_{\alpha /2,n - p}}\sqrt {\hat \sigma _\varepsilon ^2{\mathit{\boldsymbol{Z}}^{\rm{T}}}{{\left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}}} \right)}^{ - 1}}\mathit{\boldsymbol{Z}}} } \right\}. $ | (21) |
2) 最优设计变量的计算
根据数据和以上分析,设计变量的求解问题就转化成质量特性的置信水平最大化的问题
| $ \begin{array}{*{20}{c}} {\max 1 - \alpha ,}\\ {{\rm{st}}.\;\;\;\mathit{\boldsymbol{z}} \in {\mathit{\Omega }_z}.} \end{array} $ | (22) |
式中:Ωz表示设计变量的取值范围.采用优化算法即可求得最优设计变量组合zop,再通过解码得到最优设计变量组合的真实值xop.
2.2 容差设计阶段步骤一 容差成本试验设计.根据实际工程情况,确定设计变量的容差范围,设计并运行容差成本试验,采集容差成本试验数据.
步骤二 均值方差模型和容差成本模型构建.根据步骤二的响应曲面模型,分别构建基于设计变量及其容差的均值和方差模型,进而得到最优设计变量情况下均值和方差关于容差的模型;另外,根据步骤四获得的试验数据,拟合得到设计变量的容差成本模型.
1) 质量特性y的均值和方差模型
通过对设计变量zi进行解码,由式(8)可以得到质量特性y关于设计变量真实值x=(x1, x2, …xm)的响应曲面模型
| $ \hat y\left( \mathit{\boldsymbol{x}} \right) = {{\hat \gamma }_0} + \sum\limits_{i = 1}^m {{{\hat \gamma }_i}{x_i}} + \sum\limits_{i = 1}^m {{{\hat \gamma }_{ii}}x_i^2} + \sum\limits_{i = j}^m {\sum\limits_{i < j}^m {{{\hat \gamma }_{ij}}{x_i}{x_j}} } . $ | (23) |
式中:
实际工程中设计变量xi是一个在标称值Δi附近变化的随机变量,服从以标称值为均值的正态分布.那么假设设计变量xi服从正态分布N(Δi, σxi2),通过泰勒公式展开可以得到均值和方差估计模型
| $ \hat \mu \left( \mathit{\boldsymbol{x}} \right) = \hat y\left( \mathit{\boldsymbol{x}} \right) + \frac{1}{2}\sum\limits_{i = 1}^m {{{\hat \gamma }_{ii}}\sigma _{{x_i}}^2} , $ | (24) |
| $ {{\hat \sigma }^2}\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{i = 1}^m {{{\left( {{{\hat \gamma }_i} + 2{{\hat \gamma }_{ii}}{x_i} + \sum\limits_{j = i + 1}^m {{{\hat \gamma }_{ij}}{x_j}} + \sum\limits_{j = 1}^{i - 1} {{{\hat \gamma }_{ji}}{x_j}} } \right)}^2}\sigma _{{x_i}}^2} . $ | (25) |
由于设计变量的容差与其方差之间普遍存在ti=3σi的关系,故式(15)和(16)可写成
| $ \hat \mu \left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{t}}} \right) = \hat y\left( \mathit{\boldsymbol{x}} \right) + \frac{1}{{18}}\sum\limits_{i = 1}^m {{{\hat \gamma }_{ii}}t_i^2} , $ | (26) |
| $ {{\hat \sigma }^2}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{t}}} \right) = \frac{1}{9}\sum\limits_{i = 1}^m {{{\left( {{{\hat \gamma }_i} + 2{{\hat \gamma }_{ii}}{x_i} + \sum\limits_{j = i + 1}^m {{{\hat \gamma }_{ij}}{x_j}} + \sum\limits_{j = 1}^{i - 1} {{{\hat \gamma }_{ji}}{x_j}} } \right)}^2}t_i^2} . $ | (27) |
式中:t=(t1, t2…tm).因此,在最优设计变量组合xop=(x1;op, x2;op, …xm; op)情况下,均值和方差关于容差t的公式为
| $ \hat \mu \left( {{\mathit{\boldsymbol{x}}_{{\rm{op}}}},t} \right) = \hat y\left( {{\mathit{\boldsymbol{x}}_{{\rm{op}}}}} \right) + \frac{1}{{18}}\sum\limits_{i = 1}^m {{{\hat \gamma }_{ii}}t_i^2} , $ | (28) |
| $ \begin{array}{*{20}{c}} {{{\hat \sigma }^2}\left( {{\mathit{\boldsymbol{x}}_{{\rm{op}}}},\mathit{\boldsymbol{t}}} \right) = \frac{1}{9}\sum\limits_{i = 1}^m {\left( {{{\hat \gamma }_i} + 2{{\hat \gamma }_{ii}}{x_{i;{\rm{op}}}} + \sum\limits_{j = i + 1}^m {{{\hat \gamma }_{ij}}{x_{j;{\rm{op}}}}} + } \right.} }\\ {{{\left. {\sum\limits_{j = 1}^{i - 1} {{{\hat \gamma }_{ji}}{x_{j;{\rm{op}}}}} } \right)}^2}t_i^2 + \sigma _\varepsilon ^2.} \end{array} $ | (29) |
2) 容差成本模型
容差设计是通过缩小设计变量的容差来进一步减少产品的变异性.虽然较小的容差可以降低设计变量波动进而提高稳健性,但是需要更精确的设备和操作程序以及更好的技术人员, 这些都会促使投入的成本上升.因此,在容差设计阶段,设计师需要从经济性的角度研究设计变量的容差范围与质量、成本之间的关系,对质量和成本进行综合决策.目前不少学者已经对设计变量容差和成本之间的数学关系做了研究.依据设计变量的特点,常用模型有倒数模型、倒数平方模型、指数模型和幂函数模型等[15],这些模型的计算公式如表 1所示.
| 表 1 各类容差成本模型 Table 1 Various tolerance cost models |
以容差成本模型为幂函数模型为例可得总容差成本模型
| $ C\left( \mathit{\boldsymbol{t}} \right) = \sum\limits_{i = 1}^m {{c_i}\left( {{t_i}} \right)} = \sum\limits_{i = 1}^m {{\eta _{0;i}}} + \sum\limits_{i = 1}^m {{\eta _{1;i}}t_i^{ - {\eta _2}}} . $ | (30) |
步骤三 容差设计的目标优化.结合步骤五中的均值和方差模型以及容差成本模型,得到最优设计变量水平组合情况下的期望质量损失函数,再根据因子响应试验数据和容差成本试验数据,得到质量损失函数系数.由期望质量损失函数和容差成本模型构造总成本函数,通过最小化产品过程的总成本,得到最优设计变量的容差水平.
1) 质量损失函数系数的计算
克劳修斯首先提出熵的概念,之后香农将其引入到信息论中,用于评价指标属性或方案相对重要程度.熵经常被用于度量随机试验的不确定性,即相应随机变量取值的不确定性,故而可以将其用于度量作为随机向量的质量成本的波动[20].因此本文运用熵权法计算质量损失成本和容差成本的权重,进而得到质量损失函数系数wop,其计算步骤如下.
a) 建立关于质量波动和容差成本的评价指标矩阵:
假设对最优设计变量xop,在试验过程中对Q个不同容差水平的组合进行采样.根据试验数据可以构造出如下评价矩阵E
| $ \mathit{\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}} {{e_{{\rm{Loss;1}}}}}&{{e_{{\rm{C;1}}}}}\\ {{e_{{\rm{Loss;2}}}}}&{{e_{{\rm{C;2}}}}}\\ \cdots&\cdots \\ {{e_{{\rm{Loss;}}q}}}&{{e_{{\rm{C;}}q}}}\\ \cdots&\cdots \\ {{e_{{\rm{Loss;}}Q}}}&{{e_{{\rm{C;}}Q}}} \end{array}} \right]. $ | (31) |
式中:eLoss; q为试验中第q个容差组合的质量波动数据,eC; q为试验中第q个容差组合的容差成本数据,q=1, 2, …Q.
b) 规一化评价指标矩阵
质量波动和容差成本都为望小特性,故质量波动的规一化过程如下
| $ \begin{array}{*{20}{c}} {{d_{{\rm{Loss;}}q}} = \left\{ \begin{array}{l} \frac{{\max \left( {{e_{{\rm{Loss;}}q}}} \right) - {e_{{\rm{Loss;}}q}}}}{{\max \left( {{e_{{\rm{Loss;}}q}}} \right) - \min \left( {{e_{{\rm{Loss;}}q}}} \right)}},\\ 1, \end{array} \right.}\\ {\max \left( {{e_{{\rm{Loss;}}q}}} \right) \ne \min \left( {{e_{{\rm{Loss;}}q}}} \right)}\\ {\max \left( {{e_{{\rm{Loss;}}q}}} \right) = \min \left( {{e_{{\rm{Loss;}}q}}} \right).} \end{array} $ | (32) |
式中:max(eLoss; q)为在Q个容差组合中质量波动的最大值,min(eLoss; q)为在Q个容差组合中质量波动的最小值.类似地,可对容差成本进行规一化.
c) 对规一化矩阵求fLoss; q
| $ {f_{{\rm{Loss;}}q}} = \frac{{{d_{{\rm{Loss;}}q}}}}{{\sum\limits_{q = 1}^Q {{d_{{\rm{Loss;}}q}}} }}. $ | (33) |
式中fLoss; q为第q次试验中质量波动所占的比重.
d) 计算质量波动和容差成本的熵
| $ {S_{{\rm{Loss;}}q}} = \left\{ {\begin{array}{*{20}{c}} {{f_{{\rm{Loss;}}q}}\ln \left( {{f_{{\rm{Loss;}}q}}} \right),}&{{f_{{\rm{Loss;}}q}} \ne 0;}\\ {0,}&{{f_{{\rm{Loss}}q}} = 0.} \end{array}} \right. $ | (34) |
| $ {H_{{\rm{Loss}}}} = - \frac{1}{{\ln Q}}\sum\limits_{q = 1}^Q {{S_{{\rm{Loss;}}q}}} . $ | (35) |
式中HLoss为质量损失成本的熵,类似地,可得容差成本的熵HC.
e) 计算质量波动和容差成本的熵权
| $ {w_{{\rm{Loss}}}} = \frac{{1 - {H_{{\rm{Loss}}}}}}{{2 - \left( {{H_{{\rm{Loss}}}} + {H_{\rm{C}}}} \right)}}. $ | (36) |
式中wLoss为质量波动的熵权,且0≤wLoss≤1.同样可得到容差成本的熵权wC,且满足0≤wC≤1和wLoss+wC=1.熵值越大,说明所能提供的信息量越小.
f) 计算最优设计变量xop情况下质量损失函数的尺度系数wop
| $ {w_{{\rm{op}}}} = \frac{{{w_{{\rm{Loss}}}}}}{{{w_{\rm{C}}}}} = \frac{{1 - {H_{{\rm{Loss}}}}}}{{1 - {H_{\rm{C}}}}}. $ | (37) |
式中wC≠0
2) 最优容差的计算
由质量损失成本和容差成本,可以构成最优设计变量情况下的总成本函数
| $ {C_{\rm{M}}}\left( {{\mathit{\boldsymbol{x}}_{{\rm{op}}}},\mathit{\boldsymbol{t}}} \right) = E\left\{ {L\left[ {y\left( {{\mathit{\boldsymbol{x}}_{{\rm{op}}}}} \right)} \right]} \right\} + C\left( \mathit{\boldsymbol{t}} \right). $ | (38) |
其中E{L[y(xop)]}是根据质量特性的类型,将最优设计变量组合xop及质量损失函数系数wop代入式(2)、(4)和(6)中计算得出.
通过最小化总成本,将产品的参数和容差经济性设计问题转化为如下数学问题:
| $ \begin{array}{*{20}{c}} {\min {C_{\rm{M}}}\left( {{\mathit{\boldsymbol{x}}_{{\rm{op}}}},\mathit{\boldsymbol{t}}} \right) = E\left\{ {L\left[ {y\left( {{\mathit{\boldsymbol{x}}_{{\rm{op}}}}} \right)} \right]} \right\} + C\left( \mathit{\boldsymbol{t}} \right),}\\ {{\rm{st}}{\rm{.}}\;\;\mathit{\boldsymbol{t}} \in {\mathit{\Omega }_t}.} \end{array} $ | (39) |
式中Ωt表示设计变量容差的取值范围.采用非线性优化算法即可计算出最优设计变量的容差值.
本文方法尽可能地提高质量特性的置信水平,减少模型参数不确定性的影响;同时充分地利用了试验数据客观信息,确定质量损失的尺度系数,进而使成本模型和优化结果更加合理可信.
3 案例研究Myers和Montgomery[21]最早对树脂生产过程的胺添加试验进行分析,之后Kim等[15]对其进行了研究.胺添加行为对树脂粘度有较大的影响,因此需要同时从产品过程的稳健性和经济性角度对其进行参数和容差优化设计.
3.1 树脂生产过程的胺添加试验步骤一 本文以温度(x1)、搅拌速度(x2)和添加速度(x3)为设计变量,研究了它们对质量特性树脂粘度(y)的影响.设计变量真实值的取值范围为:150≤x1≤200、5≤x2≤10和15≤x3≤25;质量特性为望目特性,其约束范围为:54≤y≤58,目标值T=55.对设计变量的真实值进行编码,得到真实值的编码值如表 2所示.采用Box-Behnken试验设计方法运行因子响应试验并采集数据,如表 3所示,其中z1、z2、z3分别表示配方因子x1、x2、x3的编码值.
| 表 2 设计变量及其水平 Table 2 Design variables and their levels |
步骤二 根据表 3中因子响应试验的数据,用响应曲面法拟合得到形如式(8)的二阶模型
| 表 3 因子响应试验数据 Table 3 Data of factor response experiment |
| $ \begin{array}{l} \hat y\left( \mathit{\boldsymbol{z}} \right) = 62 + {z_1} + 2.625{z_2} - 2.375{z_3} - 7.375z_1^2 + \\ \;\;\;\;\;\;\;\;\;\;1.875z_2^2 - 3.625z_3^2 - 2{z_1}{z_2} + 11{z_1}{z_3} + 1.75{z_2}{z_3}, \end{array} $ |
步骤三 由于y为望目质量特性,采用式(19)可以计算y(z)在约束范围54≤y≤58上的置信水平.通过最大化质量特性y(z)的置信水平,构建形如式(22)的优化目标
| $ \begin{array}{*{20}{c}} {\max 1 - \alpha = pro\left\{ {54 \le y\left( \mathit{\boldsymbol{z}} \right) \le 58} \right\}}\\ {{\rm{st}}{\rm{.}}\;\;{z_{{\rm{L}};i}} \le {z_i} \le {z_{{\rm{U}};i}}}\\ {i = 1,2,3} \end{array} $ |
式中zL; i和zU; i分别表示zi的取值范围下限和上限.由案例数据及相关分析知道n=15、p=10.运用Matlab软件进行编程计算优化结果,得到最优设计变量组合(-0.66, 0.18, 0.28),经解码,其真实值组合为(158.5, 7.95, 21.4),此时的置信水平为0.972.
步骤四 通过查阅相关文献,可以知道设计变量容差的取值范围分别为:7≤t1≤10,0.35≤t2≤0.55,0.6≤t3≤0.9.按照容差取值范围,运行容差成本试验并采集试验数据如表 4所示,其中c1、c2、c3分别表示三种设计变量的容差成本.
| 表 4 容差成本试验数据 Table 4 Data of tolerance cost experiment |
步骤五 通过对设计变量编码值解码,将步骤中二的响应曲面模型,转化为质量特性关于设计变量实际值的数学关系模型
| $ \begin{array}{l} \hat y\left( \mathit{\boldsymbol{x}} \right) = - 58.875 + 2.650{x_1} - 0.65{x_2} - 11.125{x_3} - \\ \;\;\;\;\;\;\;\;\;\;\;0.012x_1^2 + 0.3x_2^2 - 0.145x_3^2 - 0.032{x_1}{x_2} + \\ \;\;\;\;\;\;\;\;\;\;\;0.088{x_1}{x_3} + 0.14{x_2}{x_3}. \end{array} $ |
通过分析质量特性的数学模型,可知估计误差的方差为2.25.将上式和相关数据代入式(26)和(27),可得质量特性均值和方差关于设计变量及其容差的模型
| $ \begin{array}{l} \hat \mu \left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{t}}} \right) = - 58.875 + 2.650{x_1} - 0.65{x_2} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;11.125{x_3} - 0.012x_1^2 + 0.3x_2^2 - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;0.145x_3^2 - 0.032{x_1}{x_2} + 0.088{x_1}{x_3} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;0.14{x_2}{x_3} + 6.667 \times {10^{ - 3}}t_1^2 + 0.017t_2^2 + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;8.056 \times {10^{ - 3}}t_3^2, \end{array} $ |
| $ \begin{array}{l} {{\hat \sigma }^2}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{t}}} \right) = 2.25 + \frac{1}{9} \times \left( {2.650 - 0.024{x_1} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left. {0.032{x_2} + 0.088{x_3}} \right)^2}t_1^2 + \frac{1}{9} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( { - 0.65 + 0.6{x_2} + 0.14{x_3} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left. {0.032{x_1}} \right)^2}t_2^2 + \frac{1}{9} \times \left( { - 11.125 - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left. {0.145{x_3} + 0.088{x_1} + 0.14{x_2}} \right)^2}t_3^2. \end{array} $ |
另外,根据本案例的实际情况并结合相关工程师的意见,本文采用幂函数模型来拟合容差成本的模型.由表 4中试验数据,得各设计变量容差成本的模型
| $ {{\hat c}_1}\left( {{t_1}} \right) = 0.132 + 1.9474t_1^{ - 0.6051}, $ |
| $ {{\hat c}_2}\left( {{t_2}} \right) = 0.141 + 0.3956t_2^{ - 0.7820}, $ |
| $ {{\hat c}_3}\left( {{t_3}} \right) = 0.106 + 0.5280t_3^{ - 0.8173}. $ |
将以上各容差成本模型代入式(30)中,可得总容差成本模型为
| $ \begin{array}{l} \hat C\left( \mathit{\boldsymbol{t}} \right) = 0.379 + 1.9474t_1^{ - 0.6051} + 0.3956t_2^{ - 0.7820} + \\ \;\;\;\;\;\;\;\;\;\;\;0.5280t_3^{ - 0.8173}. \end{array} $ |
步骤六 将得到的最优设计变量xop代入式(28)和(29)中,可以得到在最优设计变量情况下均值和方差关于容差的函数为
| $ \begin{array}{l} \hat \mu \left( {{\mathit{\boldsymbol{x}}_{{\rm{op}}}},\mathit{\boldsymbol{t}}} \right) = 50.98 + 6.667 \times {10^{ - 3}}t_1^2 + 0.017t_2^2 + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;8.056 \times {10^{ - 3}}t_3^2, \end{array} $ |
| $ {{\hat \sigma }^2}\left( {{\mathit{\boldsymbol{x}}_{{\rm{op}}}},\mathit{\boldsymbol{t}}} \right) = 2.25 + 0.025t_1^2 + 0.464t_2^2 + 0.077t_3^2. $ |
由于该质量特性为望目质量特性,因此由式(2)得期望质量损失成本
| $ \begin{array}{*{20}{c}} {E\left\{ {L\left[ {y\left( {{\mathit{\boldsymbol{x}}_{{\rm{op}}}}} \right)} \right]} \right\} = {w_{{\rm{op}}}}E{{\left[ {y\left( {{\mathit{\boldsymbol{x}}_{{\rm{op}}}}} \right) - T} \right]}^2} = }\\ {{w_{{\rm{op}}}}\left\{ {{{\hat \sigma }^2}\left( {{\mathit{\boldsymbol{x}}_{{\rm{op}}}},\mathit{\boldsymbol{t}}} \right) + {{\left[ {\hat \mu \left( {{\mathit{\boldsymbol{x}}_{{\rm{op}}}},\mathit{\boldsymbol{t}}} \right) - T} \right]}^2}} \right\}.} \end{array} $ |
由表 3中的容差成本数据,计算各容差组合情况下的质量损失成本和容差成本,再根据式(31)-(36)计算得到质量损失成本和容差成本的熵权分别为0.378 4和0.621 6,此时质量损失函数系数wop为0.608 8.再由式(38)即可得总成本函数,进而将容差设计问题转化为形如式(39)的优化目标.
| $ \begin{array}{*{20}{c}} {\min {{\hat C}_{\rm{M}}}\left( {{\mathit{\boldsymbol{x}}_{{\rm{op}}}},\mathit{\boldsymbol{t}}} \right) = 0.6088 \times \left\{ {{{\hat \sigma }^2}\left( {{\mathit{\boldsymbol{x}}_{{\rm{op}}}},\mathit{\boldsymbol{t}}} \right) + } \right.}\\ {\left. {{{\left[ {{{\hat \mu }_{{\rm{op}}}}\left( {{\mathit{\boldsymbol{x}}_{{\rm{op}}}},\mathit{\boldsymbol{t}}} \right) - 55} \right]}^2}} \right\} + \hat C\left( {{\mathit{\boldsymbol{x}}_{{\rm{op}}}},\mathit{\boldsymbol{t}}} \right),}\\ {{\rm{st}}{\rm{.}}\;\;\;\;\;t \in {\mathit{\Omega }_t}} \end{array} $ |
运用Matlab软件的Global Optimization Toolbox工具箱并采用DIRECT算法进行寻优,得最优设计变量组合xop情况下的最优容差值top为(10, 0.55, 0.9),此时总成本为9.226 2.
3.2 比较研究为了说明本文方法的有效性,采用文献[15]中的方法做对比分析.该方法对设计变量及其容差进行并行优化设计,但是没有考虑模型参数的不确定性以及如何确定质量损失函数系数.文献[15]优化目标为
| $ \begin{array}{*{20}{c}} {\min ETC = \left\{ {{{\hat \sigma }^2}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{t}}} \right) + {{\left[ {\hat \mu \left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{t}}} \right) - 55} \right]}^2}} \right\} + \hat C\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{t}}} \right),}\\ {{\rm{st}}{\rm{.}}\;\;\mathit{\boldsymbol{x}} \in {\mathit{\Omega }_x},}\\ {t \in {\mathit{\Omega }_t}.} \end{array} $ |
通过优化得到最优设计变量及其容差值分别为(177.77, 5.66, 25)和(7, 0.55, 0.73).本文方法与该方法的相关质量指标对比如表 5所示.
由表 5可见:文献[15]方法比本文方法计算得到的质量特性值更接近目标值,但是采用本文方法计算得到最优设计变量时,质量特性值在约束区间的置信水平为0.972,也就是有97.2%的可能落在该区间内,这要远高于文献[15]方法;另外,本文方法的质量损失成本和容差成本都远小于文献[15]方法.显然,本文方法所得优化结果的经济性都要优于文献[15]方法.
4 结论参数和容差设计是目前产品设计中的热点问题.同时对参数和容差进行经济性设计,有助于降低生产运作成本并提高产品可靠性.然而目前此方面的研究,忽视了模型参数不确定性和质量损失函数系数对优化结果的影响.因此,本文同时考虑这两方面的问题,通过最大化置信水平的方法得到最优设计变量,并采用熵权法求取此时的质量损失函数系数,进而得到最优容差值.值得注意的是,本文方法解决的是单质量特性的参数和容差设计问题,如何针对多元质量特性的产品过程解决多个响应间的冲突和相关性问题,将是下一步的研究方向.
| [1] |
KACKAR R N.
Quality control, robust design, and the Taguchi method[M]. New York: Springer, 1989: 176-188.
|
| [2] |
TAGUCHI G, CHOWDHURY S, WU Y.
Taguchi's quality engineering handbook[M]. New York: John Wiley & Sons, 2004.
|
| [3] |
SHOEMAKER A C, TSUI K L, WU C F J. Economical experimentation methods for robust design[J].
Technometrics, 1991, 33(4): 415-427.
DOI: 10.2307/1269414 |
| [4] |
VINING G G, MYERS R H. Combining Taguchi and response surface philosophies: a dual response approach[J].
Journal of Quality Technology, 1990, 22(1): 38-45.
|
| [5] |
APLEY D W, KIM J. A cautious approach to robust design with model parameter uncertainty[J].
ⅡE Transactions, 2011, 43(7): 471-482.
DOI: 10.1080/0740817X.2010.532854 |
| [6] |
SARIKAYA M, GULLU A. Taguchi design and response surface methodology based analysis of machining parameters in CNC turning under MQL[J].
Journal of Cleaner Production, 2014, 65(4): 604-616.
DOI: 10.1016/j.jclepro.2013.08.040 |
| [7] |
顾晓光, 马义中, 刘健, 等. 基于置信区间的多元质量特性满意参数设计[J].
系统工程与电子技术, 2015, 37(11): 2536-2545.
GU Xiaoguang, MA Yizhong, LIU Jian, et al. Satisfactory parameter design approach based on confidence interval for multivariate quality characteristics[J]. Systems Engineering and Electronics, 2015, 37(11): 2536-2545. DOI: 10.3969/j.issn.1001-506X.2015.11.18 |
| [8] |
JIN Q, LIU S, WANG P. Optimal tolerance design for products with non-normal distribution based on asymmetric quadratic quality loss[J].
The International Journal of Advanced Manufacturing Technology, 2015, 78(1): 667-675.
DOI: 10.1007/s00170-014-6681-y |
| [9] |
ZHAO Y M, LIU D S, WEN Z J. Optimal tolerance design of product based on service quality loss[J].
The International Journal of Advanced Manufacturing Technology, 2016, 82(9): 1715-1724.
DOI: 10.1007/s00170-015-7480-9 |
| [10] |
ZHANG Y, LI L, SONG M, et al. Optimal tolerance design of hierarchical products based on quality loss function[J].
Journal of Intelligent Manufacturing, .
DOI: 10.1007/s10845-016-1238-6 |
| [11] |
PENG H P, JIANG X J, LIU X J. Concurrent optimal allocation of design and process tolerances for mechanical assemblies with interrelated dimension chains[J].
International Journal of Production Research, 2008, 46(24): 6963-6979.
DOI: 10.1080/00207540701427037 |
| [12] |
SHIN S, KONGSUWON P, CHO B R. Development of the parametric tolerance modeling and optimization schemes and cost-effective solutions[J].
European Journal of Operational Research, 2010, 207(3): 1728-1741.
DOI: 10.1016/j.ejor.2010.07.009 |
| [13] |
PENG H P. Concurrent tolerancing for design and manufacturing based on the present worth of quality loss[J].
The International Journal of Advanced Manufacturing Technology, 2012, 59(9): 929-937.
DOI: 10.1007/s00170-011-3542-9 |
| [14] |
BISGAARD S, ANKENMAN B. Analytic parameter design[J].
Quality Engineering, 1995, 8: 75-91.
DOI: 10.1080/08982119508904606 |
| [15] |
Kim Y J, Cho B R. Economic integration of design optimization[J].
Quality Engineering, 2000, 12(4): 561-567.
DOI: 10.1080/08982110008962621 |
| [16] |
JEANG A. Combined parameter and tolerance design optimization with quality and cost[J].
International Journal of Production Research, 2001, 39(5): 923-952.
DOI: 10.1080/00207540010006717 |
| [17] |
He Z, Zhang Z H, Li B G, et al. Improvement of economic integration of design with process capability index[J].
Total Quality Management & Business Excellence, 2009, 11(20): 1255-1262.
DOI: 10.1080/14783360903254946 |
| [18] |
张志红, 何桢. 考虑噪声因子的参数和公差经济性设计策略[J].
管理科学学报, 2012, 15(3): 61-71.
ZHANG Zhihong, HE Zhen. Strategy of economic parameter and tolerance design with noise factors considered[J]. Journal of Management Sciences in China, 2012, 15(3): 61-71. |
| [19] |
MONTGOMERY D C.
Design and analysis of experiments(6th)[M]. New York: John Wiley & Sons, 2005.
|
| [20] |
欧阳林寒, 马义中, 汪建均, 等. 基于熵权理论和双响应曲面的稳健设计[J].
管理工程学报, 2014, 28(2): 191-195.
OUYANG Linhan, MA Yizhong, WANG Jianjun, et al. Robust design based on entropy weight and dual response surface[J]. Journal of Industrial Engineering/Engineering Management, 2014, 28(2): 191-195. DOI: 10.3969/j.issn.1004-6062.2014.02.025 |
| [21] |
MYERS R H, MONTGOMERY D C.
Response surface methodology[M]. New York: John Wiley & Son, 1995.
|
 2017, Vol. 49
2017, Vol. 49


