煤粉燃烧过程常被作为能量的提供者应用于不同工业[1].研究发现升温制度对煤粉燃烧过程有重要的影响.然而,前人关于升温速率对煤粉燃烧过程的影响主要是定性分析,定量研究较少[2-3].参考文献[4]提出一种预测不同升温速率下煤粉热解过程动力学常数的方法.其表达式为k1/k2=(m1/m2)n,其中,k为热解反应速率常数,m为升温速率,指数n为升温速率对煤热解反应速率的影响程度.然而,关系式只能简单计算k的平均值.忽略温度对速率常数的影响,没有给出速率常数k与温度和升温速率的关系式.因此,表达式不能直接用来描述煤粉燃烧动力学过程.所以本文重点研究升温速率对煤粉燃烧过程动力学的影响.
在等温条件下,Arrhenius方程常用来描述反应速率常数与温度之间的关系.随着热分析动力学的发展,Arrhenius方程被应用到非等温领域.然而,无论采用哪种热力学分析方法(如:模型拟合法[5],等转化率法[6],分布活化能法(DAEM)[7]),在相同温度下活化能Ea和速率常数k都会随着升温速率β的变化而改变.因此,本文提出一个Arrhenius方程修正式来描述升温速率β对反应速率常数k的影响.
1 实验实验过程中所用煤粉试样取自某钢铁厂1#高炉的喷吹煤粉,其工业分析和元素分析见表 1,粒度分布见表 2.
| 表 1 煤粉工业分析与元素分析结果 Table 1 Proximate and ultimate analysis of pulverized-coal used in the experiment |
| 表 2 煤粉粒度分布 Table 2 Particle size distribution of pulverized-coal used in theexperiment |
实验仪器采用北京恒久科学仪器厂生产HCT-1综合热分析仪,按照设定程序自动升温,期间实验数据由计算机自动采集.每次实验所用试样质量为10±0.2 mg.将煤粉试样放入到Al2O3坩埚内,由室温25 ℃以10 ℃/min升温至105 ℃恒温10 min,以除去样品中的吸附水;以不同的升温速率(20 ℃/min、25 ℃/min、30 ℃/min和35 ℃/min)加热到950 ℃.在整个实验过程中采用气流量150 mL/min的空气作为载气.
3.4小结中为验证Arrhenius方程修正式在其它升温速率下的外推性,又对升温速率10 ℃/min、15 ℃/min、40 ℃/min和45 ℃/min煤粉燃烧过程进行实验.
2 结果与讨论 2.1 升温速率对煤粉燃烧过程的影响本文采用热重分析法对实验数据进行分析处理,图 1、2分别给出不同升温速率下煤粉燃烧过程的转化率(α)和反应速率(dα/dT)曲线图.其中,反应速率曲线是转化率曲线的一次微分曲线.

|
图 1 不同升温速率下的煤粉燃烧过程转化率曲线 Figure 1 Fractional conversion curves of pulverized-coal combustion at different heating rates |
|
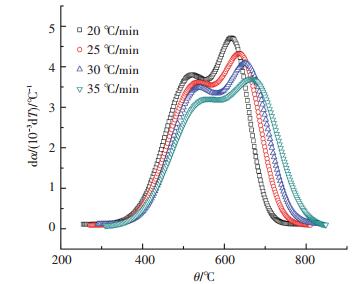
图 2 不同升温速率下的煤粉燃烧过程反应速率曲线(dα/dT) Figure 2 Reaction rate curves of pulverized-coal combustion at different heating rates (dα/dT) |
根据实际应用情况,本文主要研究从着火点到燃尽点(Ti~Tb)的燃烧过程动力学.由图 1、2可知,曲线形状相似,随升温速率提高整个曲线向右偏移.整个燃烧过程表现出明显的滞后性[8].从图 2可看出,每条反应速率曲线都有两个峰值和一个波谷[9],从燃烧反应宏观动力学方面入手,现象被认为是由于反应机理和控速环节的改变而导致.因此,以燃烧反应速率曲线中波谷值所对应温度点将燃烧过程中着火点到燃尽点的温度区间(Ti~Tb)分为两个阶段,结果见表 3.由表 3可知,在非等温条件下,不同升温速率下温度区间划分也不相同.
| 表 3 不同升温速率下的反应温度区间、峰值温度、特征温度点 Table 3 Reaction regions, peaks, and characteristic temperatures at different heating rates |
第一阶段,主要是挥发分的析出和燃烧过程[10].例如:液体和气体产物大量生成、脱挥发分作用,以及挥发分的燃烧过程.此外,由表 3可看出,粉煤着火点温度Ti随升温速率增加而增加,而不是一个常数.因此,着火点温度不仅与煤的性能有关,而且还受升温速率的影响.
第二阶段,主要是焦炭的氧化过程.分为3个步骤:空气中的氧扩散到碳表面,碳和氧的表面化学反应,气体反应产物的扩散过程[11].随着反应进行,温度逐渐升高,化学反应速率逐渐加快并超过扩散速率.因此,控速环节的改变是图 2中出现双峰的主要原因.
2.2 Arrhenius方程修正式在无限小的时间范围内,非等温过程被看成等温过程.其反应速率为
| $ {\rm{d}}\alpha /{\rm{d}}t = k\left( T \right)f\left( \alpha \right). $ | (1) |
式中:f(α)为反应模型;α为转化率;t为时间,单位是s;k(T)为反应速率常数,单位是s-1;T为温度,单位是K.
样品的转化率α为
| $ \alpha = \left( {{m_0}-{m_t}} \right)/\left( {{m_0}-{m_{{\rm{final}}}}} \right). $ | (2) |
式中:m0为样品初始质量,单位是g;mt为样品在t时刻的质量,单位是g;mfinal为样品最终反应的剩余质量,单位是g.
将Arrhenius方程k(T)=Aexp(-Ea/RT)和升温速率的关系式dT=βdt代入到式(1)中.其近似积分式为[12]
| $ G\left( \alpha \right) = \int\limits_0^\alpha {\frac{{{\rm{d}}\alpha }}{{f\left( \alpha \right)}}} = \int\limits_{{T_0}}^{{T_t}} {\frac{k}{\beta }} {\rm{d}}T = \int\limits_{{T_0}}^{{T_t}} {\frac{{A{e^{-\frac{{{E_{\rm{a}}}}}{{RT}}}}}}{\beta }} {\rm{d}}T \approx \frac{{AR{T^2}}}{{\beta {E_{\rm{a}}}}}\exp \left( {-\frac{{{E_{\rm{a}}}}}{{RT}}} \right). $ | (3) |
式中:G(α)为f(α)-1的积分式;Ea为活化能,单位是J·mol-1;A为指前因子,单位是s-1;R为理想气体常数,值为8.314 J·(K·mol)-1;β为升温速率,单位是K·s-1.
在同一升温速率下,升温速率β为一个定值.对式(3)取对数得
| $ \ln \frac{{G\left( \alpha \right)}}{{{T^2}}} = \ln \frac{{AR}}{{\beta {E_{\rm{a}}}}}-\frac{{{E_{\rm{a}}}}}{{RT}}. $ | (4) |
将动力学机理函数G(α)代入到式(4).根据ln[G(α)/T2]与1/T的线性关系,可求出相应的活化能和指前因子.
一般情况下,不同升温速率下的活化能Ea和指前因子A之间存在着动力学补偿效应[13],为
| $ \ln {A_i} = a{E_{{\rm{a}}i}} + b. $ | (5) |
式中下标i代表不同的升温速率.因此,指前因子为Ai=exp(aEai+b),Arrhenius方程改写为
| $ {k_i} = {A_i}{e^{-\frac{{{E_{{\rm{a}}i}}}}{{RT}}}} = {e^{a{E_{{\rm{a}}i}} + b}}{e^{-\frac{{{E_{{\rm{a}}i}}}}{{RT}}}} = {e^{{E_{{\rm{a}}i}}\left( {a-\frac{1}{{RT}}} \right) + b}}. $ | (6) |
参考文献[14]从分布活化能模型中推导出活化能Ea与升温速率β的关系式,dβ/dT=β(2/T+Ea/RT2).对其进行积分得Ea=RTln(T2)-RTln(β).本文采用不同的动力学模型G(α)来描述煤燃烧过程的相应动力学区间,研究发现升温速率对活化能的影响可表示为Eai=△Ealn βi+Ea0.因此,式(6)被修正为
| $ {k_i} = {e^{\Delta {E_{\rm{a}}}\left( {a-\frac{1}{{RT}}} \right)\ln {\beta _i}}}{e^{a{E_{{\rm{a0}}}} + b}}{e^{-\frac{{{E_{{\rm{a0}}}}}}{{RT}}}} = {\beta _i}^{\Delta {E_{\rm{a}}}\left( {a-\frac{1}{{RT}}} \right)}{A_0}{e^{ - \frac{{{E_{{\rm{a0}}}}}}{{RT}}}}. $ | (7) |
式中:A0=exp(aEa0+b),根据ln Ai和Eai与Eai和ln βi拟合曲线的斜率和截距可求出参数a、b、Ea0和△Ea.与Arrhenius方程ki(T)=Aiexp(-Eai/RT)相比,指前因子被修正为ln Ai=a△Ealn βi+ln A0.
对式(7)简化后取对数,得Arrhenius方程修正式
| $ \ln {k_i} =-{E_{{\rm{a0}}}}/RT + \Delta {E_{\rm{a}}}\left( {a-1/RT} \right)\ln {\beta _i} + \ln {A_0}. $ | (8) |
为简化k与β的关系式,由式(7)得
| $ \frac{{{k_1}}}{{{k_2}}} = \frac{{{\beta _1}^{\Delta {E_{\rm{a}}}\left( {a-\frac{1}{{RT}}} \right)}}}{{{\beta _2}^{\Delta {E_{\rm{a}}}\left( {a-\frac{1}{{RT}}} \right)}}} = {\left( {\frac{{{\beta _1}}}{{{\beta _2}}}} \right)^{\Delta {E_{\rm{a}}}\left( {a-\frac{1}{{RT}}} \right)}}. $ | (9) |
将式(9)与参考文献[4]中经验关系式k1/k2=(m1/m2)n相比可知,指数n被修正为△Ea(a-1/RT).即在不同温度下反应速率常数k的平均值被修正成一个瞬时值.
2.3 相应动力学参数求解粉煤燃烧过程属于气固多相反应.两个反应区间的反应机理不同,如果只采用单一模型来拟合整个燃烧过程显然是不合理的[15].因此本文采用分段的方法来拟合煤粉燃烧的动力学过程.在第一阶段,由于温度相对较低,反应产物较少,气体反应物和生成物易穿过固体产物层.燃烧过程主要控速环节是化学反应过程.因此,第一阶段采用界面化学反应模型来进行拟合[16].随温度升高,反应进行,界面化学反应速率逐渐升高.与此同时,固体产物逐渐积累,气体反应物和产物的扩散过程受到阻碍.控速环节由界面化学反应变为扩散过程.因此,第二阶段采用内扩散模型来进行拟合.对应的机理函数见表 4.
| 表 4 两个反应阶段的动力学机理函数 Table 4 Kinetic mechanism functions for two reaction regions |
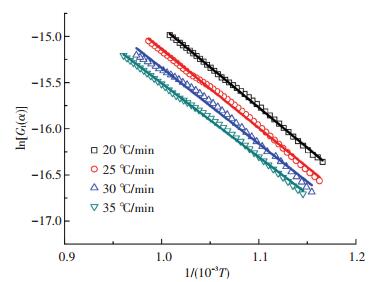
根据表 3中对应的温度区间和表 4中相应的动力学机理函数,将不同反应区间的实验点依据式(4)进行拟合,结果见图 3、4.
|
图 3 不同升温速率下第一阶段的拟合曲线 Figure 3 Model fitting curves for first region at different heating rates |

|
图 4 不同升温速率下第二阶段的拟合曲线 Figure 4 Model fitting curves for second region at different heating rates |
从图 3、4中可看出,实验点的线性关系很好.由表 5可知,所有的相关系数均超过0.99.这表明,界面化学反应模型和内扩散模型能很好地描述煤粉燃烧的两个反应阶段.根据图 3、4中拟合直线的斜率K和截距C,求得相应的活化能Ea=-RK和指前因子A=-βKexp(C),结果见表 5.
| 表 5 不同升温速率下的活化能和指前因子 Table 5 Activation energies and pre-exponential factors at different heating rates |
由表 5可知,在相同控速环节内,活化能随升温速率增加而减小.煤燃烧过程中存在着许多放热反应.在非等温条件下,升温速率越快,单位温度内积累的热量越多.因此,快速升温能促进燃烧反应,致使活化能随升温速率提高而降低[17].升温速率对活化能Ea和指前因子A有重要的影响.使得反应速率常数k随升温速率β的变化而改变.
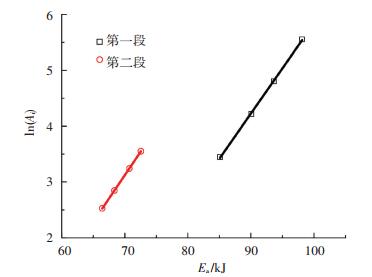
根据表 5中的数据,将不同阶段的Eai和ln Ai与Eai与ln βi分别进行拟合,结果见图 5、6.
|
图 5 活化能和指前因子之间的动力学补偿效应 Figure 5 Kinetic compensation effect between activation energy and pre-exponential factor |
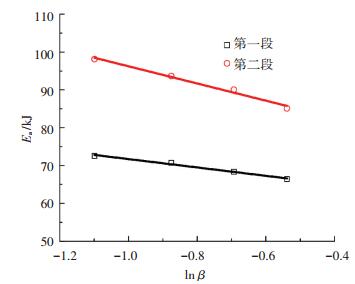
|
图 6 升温速率与活化能之间的关系 Figure 6 Relationship between heating rate and activation energy |
图 5、6中实验点的线性关系良好.由表 6可知,拟合曲线的相关系数都超过0.97.表明不同升温速率下活化能与指前因子的动力学补偿效应可表示为ln Ai=aEai+b,升温速率对活化能的影响可表示为Eai=△Ealn βi+Ea0.由拟合曲线的斜率和截距求得相应参数a、b、△Ea和Ea0,结果见表 6.将表 6中相应动力学参数代入式(8),得到不同温度区间反应速率常数ki的表达式,见表 7.
| 表 6 不同反应阶段相应的动力学参数和相关系数 Table 6 Corresponding parameters and correlation coefficients for different regions |
| 表 7 不同温度区间反应速率常数ki的表达式 Table 7 Functions of the rate constant ki for two regions |
将表 7中Arrhenius方程修正式与等温下的Arrhenius方程(ki(T)=Aiexp(-Eai/RT))对比可知,在非等温条件下,Arrhenius方程修正式中反应速率常数ki是温度T与升温速率β的二元函数.因此,在非等温条件下将升温速率β引入到Arrhenius方程中是非常有必要的.
2.4 不同升温速率下的外推性采用10 ℃/min、15 ℃/min、40 ℃/min和45 ℃/min升温速率下的煤粉燃烧过程数据,来验证Arrhenius方程修正式ln ki=-Ea0/RT+△Ea(a-1/RT)ln βi+ln(A0)的外推性.不同升温速率下的特征温度点见表 8.
| 表 8 不同升温速率下粉煤燃烧过程的特征温度 Table 8 Characteristic temperatures of pulverized-coal combustion at different heating rates |
从表 8中发现,升温速率对着火点温度Ti、波谷所对应温度Tv和燃尽点温度Tb的影响可表示为T=T0+△Tln βi.根据拟合结果求得相应的参数,见表 9.
| 表 9 特征温度的拟合结果 Table 9 Fitting results of characteristic temperatures |
由表 9可知,拟合曲线的相关系数均超过0.97.表明关系式T=T0+△Tln βi,能够用来描述升温速率对分段点温度的影响,进而可知不同升温速率下温度区间的划分.结合表 7能直接预测不同升温速率不同温度下反应速率常数k的值.
用表 4中的机理函数根据式(4)对升温速率10 ℃/min、15 ℃/min、40 ℃/min和45 ℃/min下煤粉燃烧过程的实验点进行拟合,进而求得相应的活化能Eai和指前因子Ai.随后,分别从两个温度区间各选取一个温度点500 ℃和610 ℃来对比反应速率常数ki的实验值和预测值.然后,应用不同升温速率下的活化能和指前因子,根据Arrhenius方程(ki(T)=Aiexp(-Eai/RT))计算出反应速率常数k在温度500 ℃和610 ℃的实验值见表 10.
| 表 10 不同升温速率下的反应速率常数值ki/s-1 Table 10 Reaction rate constants at different heating rates ki/s-1 |
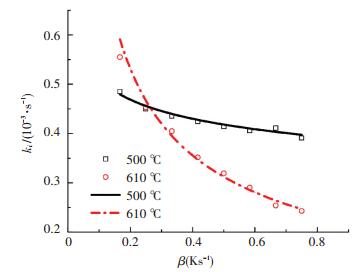
根据表 7中Arrhenius方程表达式,直接计算出相应温度(500 ℃和610 ℃)下反应速率常数k与升温速率β的预测曲线. 图 7为反应速率常数实验值和预测曲线的对比图.其中,图例点代表实验值,实线代表Arrhenius方程修正式的预测曲线.
|
图 7 反应速率常数实验值和预测值的对比 Figure 7 Comparison results between experimental data and predicted curves of reaction rate constants |
从图 7可看出,反应速率常数k值随升温速率β的增大而减小,且反应速率常数实验值与预测曲线具有良好的一致性.表明Arrhenius方程修正式对其他升温速率下具有良好的外推性.因此,只要有3组不同升温速率下煤粉燃烧过程的实验数据就能求得不同反应区间的Arrhenius方程修正式,进而求出不同温度不同升温速率下的反应速率常数.
3 结论在非等温热分析动力学过程中,本文给出一个Arrhenius方程的修正式来描述升温速率β对煤粉燃烧过程反应速率常数k的影响.
1) 随着升温速率增加,煤粉燃烧过程表现出明显的热滞后现象.根据煤粉燃烧过程的特点,以反应速率曲线达到波谷时对应的温度点,将着火点到燃尽点的燃烧过程从划分为两个阶段.随后,根据两个阶段的特点,分别采用界面化学反应模型和内扩散模型来描述相应的动力学过程.结果表明,实验数据与模型拟合的线性关系良好,所有相关系数均超过0.99.
2) 为描述升温速率对煤粉燃烧过程动力学的影响,本文给出一个Arrhenius方程的修正式ln ki=-Ea0/RT+△Ea(a-1/RT)ln βi+ln A0.其中,动力学参数a、△Ea、Ea0和A0可由3组不同升温速率下的实验值求得.研究表明修正的Arrhenius方程不仅能很好地描述升温速率对反应速率常数k的影响,而且还具有一定的外推性.
| [1] |
WU Keng, DING Rucai, YANG Sen, et al. Research on unconsumed fine coke and pulverized coal of BF dust under different PCI rates in BF at Capital Steel Co[J].
ISIJ International, 2010, 50(3): 390-395.
DOI: 10.2355/isijinternational.50.390 |
| [2] |
BORREGO A G, OSÓRIO E, CASAL M D, et al. Coal char combustion under a CO2-rich atmosphere: implications for pulverized coal injection in a blast furnace[J].
Fuel Processing Technology, 2008, 89(11): 1017-1024.
DOI: 10.1016/j.fuproc.2008.03.012 |
| [3] |
LEMAIRE R, BRUHIER C, MENAGE D, et al. Study of the high heating rate devolatilization of a pulverized bituminous coal under oxygen-containing atmospheres[J].
Journal of Analytical & Applied Pyrolysis, 2015, 114: 22-31.
DOI: 10.1016/j.jaap.2015.04.008 |
| [4] |
YU Juan, ZHANG Mingchuan. A simple method for predicting the rate constant of pulverized-coal pyrolysis at higher heating rate[J].
Energy & Fuels, 2003, 17: 1085-1090.
DOI: 10.1021/ef020281r |
| [5] |
SUN Xiaoyan, YIN Shumei, WANG Hongyuan, et al. Effect of the addition of cornstalk to coal powder/coal tar combustion[J].
Journal of Thermal Analysis and Calorimetry, 2012, 109(2): 817-823.
DOI: 10.1007/s10973-011-1769-1 |
| [6] |
许桂英, WATKINSONA P, ELLISN, 等. 亚麻纤维热解动力学的"model free"法和Coats-Redfern模型拟合法研究[J].
化工学报, 2010, 09(9): 2480-2487.
XU Guiying, WATKINSON A P, ELLIS N, et al. Kinetic study on thermal decomposition of flax fibers with model-free and Coats-Redfern model fitting kinetic approaches[J]. CIESC Journal, 2010, 09(9): 2480-2487. |
| [7] |
MIURA K C. A new and simple method to estimate f(E) and k0(E) in the Distributed Activation Energy Model from three sets of experimental data[J].
Energy & Fuels, 1995, 9: 302-307.
|
| [8] |
KOCABAS Z, OKYAY A F, YVRVM Y. Combustion characteristics of Turkish hazelnut shell biomass, lignite coal, and their respective blends via thermogravimetric analysis[J].
Journal of Thermal Analysis and Calorimetry, 2015, 119: 1723-1729.
DOI: 10.1007/s10973-014-4348-4 |
| [9] |
KÖK M V. An investigation into the combustion curves of lignites[J].
Journal of Thermal Analysis and Calorimetry, 2001, 64: 1319-1323.
DOI: 10.1023/A:1011586105543 |
| [10] |
KOK M V. Simultaneous thermogravimetry-calorimetry study on the combustion of coal samples: Effect of heating rate[J].
Energy Conversion and Management, 2012, 53(1): 40-44.
DOI: 10.1016/j.enconman.2011.08.005 |
| [11] |
XU Zhijie, SUN Xin, KHALEEL M A. A generalized kinetic model for heterogeneous gas-solid reactions[J].
Journal of Chemical Physics, 2012, 137(7): 8653-8660.
DOI: 10.1063/1.4740242 |
| [12] |
VLAEV L T, MARKOVSKA I G, LYUBCHEV L A. Non-isothermal kinetics of pyrolysis of rice husk[J].
Thermochimica Acta, 2003, 406: 1-7.
DOI: 10.1016/S0040-6031(03)00222-3 |
| [13] |
WANG Guangwei, ZHANG Jianliang, SHAO Jiugang, et al. Characterisation and model fitting kinetic analysis of coal/biomass co-combustion[J].
Thermochimica Acta, 2014, 591: 68-74.
DOI: 10.1016/j.tca.2014.07.019 |
| [14] |
刘旭光, 李保庆. 分布活化能模型的理论分析及其在半焦气化和模拟蒸馏体系中的应用[J].
燃料化学学报, 2001, 29(1): 54-59.
LIU Xuguang, LI Baoqing. Theoretical elucidation of distributed activation energy model and its applications in char gasification and simulation distillation systems[J]. Journal of Fuel Chemistry and Technology, 2001, 29(1): 54-59. |
| [15] |
巢昌耀, 吴铿, 杜瑞岭, 等. 煤粉与半焦的混合燃烧特性及动力学分析[J].
工程科学学报, 2016, 38(11): 1532-1538.
CHAO Changyao, WU Keng, DU Ruiling, et al. Combustion characteristics and kinetic analysis of pulverized coal and semicoke[J]. Chinese Journal of Engineering, 2016, 38(11): 1532-1538. DOI: 10.13374/j.issn2095-9389.2016.11.004 |
| [16] |
MAITRA S, BANDYOPADHYAY N, DAS S, et al. Non-Isothermal decomposition kinetics of alkaline earth metal carbonates[J].
Journal of the American Ceramic Society, 2007, 90(4): 1299-1303.
DOI: 10.1111/j.1551-2916.2007.01607.x |
| [17] |
LIU Xiang, CHEN Meiqian, WEI Yuanhang. Kinetics based on two-stage scheme for co-combustion of herbaceous biomass and bituminous coal[J].
Fuel, 2015, 143: 577-585.
DOI: 10.1016/j.fuel.2014.11.085 |
 2017, Vol. 49
2017, Vol. 49


