充填采矿法不仅安全性高,而且可有效减少矿石损失、贫化和解决尾矿占地难题,同时有利于矿井漏风、热害、冲击地压、矿石自燃和瓦斯积聚等灾害的防治,目前在各类矿山中应用较为广泛.
充填材料的配比不仅影响充填体强度,而且对料浆流动特性、充填成本和充填工艺决策也起到决定性作用.鉴于此,刘同有等[1]开展29组不同配比的水淬渣胶结充填实验,采用灰色关联法对充填配比进行分析优选;周科平等[2]、李夕兵等[3]分别采用遗传算法和博弈树理论对安庆铜矿分级尾砂胶结充填配比进行优化,减少水泥用量;王新民等[4]将正交实验设计方法用于充填材料配比研究领域,利用Matlab软件得出充填配比和充填体强度的线性回归方程;Chang等[5]、张钦礼等[6]基于不同配比实验分别构建膏体充填体和分级尾砂胶结充填体强度的BP神经网络预测模型;艾纯明等[7]基于均匀试验,拟合出膏体充填流动特性和质量浓度、尾废比、砂灰比的二次多项式回归关系,以膏体稳定性为目标求解充填材料最佳配比;韩斌等[8]根据36组废石胶结充填实验结果对最优配比进行直观优选;文献[9-11]分别将模糊集理论、响应面法、馄饨优化神经网络法用于充填配比优化研究,均取得一定的成效.此外,还有一些数理统计方法被用于充填配比优化,如回归正交实验法和配方实验设计等[12-13].由于充填性能参数及影响因素较多,当考虑多参数多因素时,往往需要大量试验,以致优化工作难以开展.实践表明,响应面法同比正交试验等方法可靠度较高,可以连续对试验各水平进行寻优,能够定量分析自变量及交互作用与因变量的相关关系,且多水平试验次数较少[14].基于满意度函数的响应面法可以实现对多目标整体进行优化[15],对此,本文将其用于某铁矿尾砂胶结充填最优配比研究,并探讨海水作为制浆水源的可行性及其与砂灰比、料浆质量浓度对充填体强度、流动特性和泌水性能的影响.
1 响应面-满意度函数法优化理论 1.1 响应面理论响应面理论的基本思想是通过实验设计寻找可以逼近自变量x和因变量y之间映射函数y=f(x)的响应面函数
| $ \begin{array}{l} \hat y = g\left( {{x_1},{x_2}, \cdots ,{x_n}} \right) = \sum\limits_{i = 1}^n {{\beta _{ii}}x_i^2} + \sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = 1}^n {{\beta _{ij}}{x_i}{x_j}} } + \\ \;\;\;\;\;\;\;\sum\limits_{i = 1}^n {{\beta _i}{x_i} + {\beta _0}} . \end{array} $ | (1) |
式中:
假设样本进行m次试验,Y为因变量向量,ε为误差向量,那么
| $ \mathit{\boldsymbol{Y}} = \mathit{\boldsymbol{\beta X}} + \mathit{\boldsymbol{\varepsilon }}. $ | (2) |
其中:
| $ \mathit{\boldsymbol{Y}} = {\left[ {{y^{\left( 1 \right)}},{y^{\left( 2 \right)}} \cdots ,{y^{\left( m \right)}}} \right]^{\rm{T}}};\;\;\;\;\;\mathit{\boldsymbol{\varepsilon }} = {\left[ {{\varepsilon _1},{\varepsilon _2} \cdots ,{\varepsilon _m}} \right]^{\rm{T}}}; $ |
| $ \mathit{\boldsymbol{X = }}\\ \left[ {\begin{array}{*{20}{c}} 1&{{x_1}{x_2}}& \cdots &{{x_n}}&{x_1^2}&{x_2^2}& \cdots &{x_n^2}&{{x_1}{x_2}}&{{x_1}{x_3}}& \cdots &{{x_1}{x_n}}&{{x_2}{x_3}}& \cdots &{{x_{n - 1}}{x_n}}\\ 1&{{x_1}{x_2}}& \cdots &{{x_n}}&{x_1^2}&{x_2^2}& \cdots &{x_n^2}&{{x_1}{x_2}}&{{x_1}{x_3}}& \cdots &{{x_1}{x_n}}&{{x_2}{x_3}}& \cdots &{{x_{n - 1}}{x_n}}\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots \\ 1&{{x_1}{x_2}}& \cdots &{{x_n}}&{x_1^2}&{x_2^2}& \cdots &{x_n^2}&{{x_1}{x_2}}&{{x_1}{x_3}}& \cdots &{{x_1}{x_n}}&{{x_2}{x_3}}& \cdots &{{x_{n - 1}}{x_n}} \end{array}} \right]; $ |
| $ \begin{array}{l} \mathit{\boldsymbol{\beta }} = \left[ {{\beta _0},{\beta _1},{\beta _2}, \cdots ,{\beta _n},\beta _1^2,\beta _2^2, \cdots ,\beta _n^2,{\beta _1}{\beta _2},{\beta _1}{\beta _3}, \cdots ,} \right.\\ \;\;\;\;\;\;{\left. {{\beta _1}{\beta _n},{\beta _2}{\beta _3}, \cdots ,{\beta _{n - 1}}{\beta _n}} \right]^{\rm{T}}}. \end{array} $ |
为找到最接近所有试验数据点的响应面,利用最小二乘原理使ε的平方和S(β)最小,即
| $ \min S\left( \mathit{\boldsymbol{\beta }} \right) = {\left\| \mathit{\boldsymbol{\varepsilon }} \right\|^2} = {\left( {\mathit{\boldsymbol{Y}} - \mathit{\boldsymbol{X\beta }}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{Y}} - \mathit{\boldsymbol{X\beta }}} \right). $ | (3) |
令ΔS(β)=0,化简后可得
| $ \beta = {\left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}}} \right)^{ - 1}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{Y}}. $ | (4) |
基于试验样本,根据式(4)计算待定常数,再代入式(1)即可求出自变量对应的响应面函数.响应面法基于实验设计进行响应面函数拟合和自变量显著性分析,常用的试验设计方法有中心组合设计、Box-Behnken设计和拉丁超立方设计等.
1.2 满意度函数多目标优化法根据约束条件利用式(1)一般只能逐个对响应量独立进行优化求解,对于多响应量不能同时进行整体优化,无法求出自变量最优解.对此,George等[17]率先提出多目标优化方法,并将其用于混凝土配方设计.在此基础上,本文采用Candioti等[15]提出的满意度函数法进行优化,第k(k=1, 2, …, K,K为响应量总个数)个响应量的满意度记为dk(
| $ {d_k}\left( {{{\hat y}_k}\left( x \right)} \right) = \left\{ \begin{array}{l} 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\hat y}_k}\left( x \right) < {L_k};\\ {\left( {\frac{{{{\hat y}_k}\left( x \right) - {L_k}}}{{{U_k} - {L_k}}}} \right)^s},\;\;{L_k} \le {{\hat y}_k}\left( x \right) \le {U_k};\\ 1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\hat y}_k}\left( x \right) > {U_k}. \end{array} \right. $ | (5a) |
| $ {d_k}\left( {{{\hat y}_k}\left( x \right)} \right) = \left\{ \begin{array}{l} 1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\hat y}_k}\left( x \right) < {L_k};\\ {\left( {\frac{{{U_k} - {{\hat y}_k}\left( x \right)}}{{{U_k} - {L_k}}}} \right)^s},\;\;{L_k} \le {{\hat y}_k}\left( x \right) \le {U_k};\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\hat y}_k}\left( x \right) > {U_k}. \end{array} \right. $ | (5b) |
| $ {d_k}\left( {{{\hat y}_k}\left( x \right)} \right) = \left\{ \begin{array}{l} 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\hat y}_k}\left( x \right) < {L_k};\\ {\left( {\frac{{{{\hat y}_k}\left( x \right) - {L_k}}}{{{U_k} - {L_k}}}} \right)^s},\;\;{L_k} \le {{\hat y}_k}\left( x \right) \le {U_k};\\ 1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\hat y}_k}\left( x \right) = {T_k};\\ {\left( {\frac{{{U_k} - {{\hat y}_k}\left( x \right)}}{{{U_k} - {L_k}}}} \right)^s},\;\;{T_k} \le {{\hat y}_k}\left( x \right) \le {U_k};\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\hat y}_k}\left( x \right) > {U_k}. \end{array} \right. $ | (5c) |
式中:
整体满意度D根据单满意度函数加权几何平均数求解,即
| $ D = {\left( {\prod\limits_{k = 1}^K {d_k^{{r_k}}} } \right)^{\frac{1}{{{r_1} + {r_2} + \cdots + {r_K}}}}}. $ | (6) |
式中K、rk为响应量个数和权数.响应量权数表示该响应量相对于其他响应量的重要程度,取值为1~5间的整数.
2 充填材料配比试验 2.1 工程背景某铁矿毗邻莱州湾,采选能力150万t/a.采矿标高+5~-380 m,矿体破碎松软,围岩为二长花岗岩.一直以来,矿山采用无底柱分段崩落法开采,地表塌陷坑采用选厂尾砂直接回填,第四系地层破坏严重,松散层水和海积层泥沙极易形成流沙灌入井下.鉴于此,为避免井下泥砂透出事故,矿山拟对中部采区(3#~10#勘探线)采用尾砂胶结充填法开采,因而需要对充填材料配比进行实验研究.
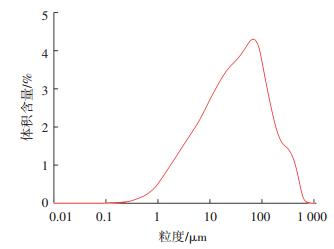
2.2 充填材料物理化学特性胶凝材料采用焦家金矿研发的尾砂专用固结材料C料,主要成分为矿渣、火山灰、石灰、石膏和添加剂.和水泥相比,它具有固化效果好,料浆流动特性好且用量可减少一半,性价比较高.尾砂选用尾矿库铁矿尾砂,室内测得尾砂的容重为15.29 kN/m3,干密度为2.55 g/cm3,含水率9.64%,孔隙率为38.8%,渗透系数为6.5 cm/h(20 ℃).采用SimensD500型X分析仪和Mastersizer3000激光衍射粒度分析仪对尾砂化学成分和粒度分布进行测定,结果见表 1、图 1.
| 表 1 尾砂主要成分 Table 1 Main compositions of tailings |
|
图 1 尾砂粒度分布曲线 Figure 1 Grain size distribution curve of tailings |
根据尾砂粒度分布曲线可计算粒径特征参数d10、d30、d50、d60和d90分别为3.53 μm、13.20 μm、32.60 μm、48.27 μm和176.04 μm,根据式(7)计算不均匀系数Cu为13.67>4~5(最佳级配),曲率系数Cc为1.02,介于1~3,这充分说明尾砂级配良好但连续性稍差,粒度分布较不均匀,细粒级含量偏多.建议工程中对尾砂进行浓密脱泥处理,从而提高料浆的泵送性能和固化效果.
| $ \left\{ \begin{array}{l} {C_u} = {d_{60}}/{d_{10}},\\ {C_c} = d_{30}^2/{d_{60}}{d_{10}}. \end{array} \right. $ | (7) |
式中:d60、d10和d30分别表示尾砂过筛重量占60%、10%和30%的粒径.
考虑淡水成本较高,研究尝试利用该矿井下排出的丰富咸水或邻近的海水作为充填水源.受地表水补给和径流影响,井下咸水和渤海海水成分基本相同,含有大量Cl-,具有一定的腐蚀性.因此,研究海水作为充填水源对充填性能的影响尤为必要.本次试验最终选择C料、尾砂、海水作为充填材料进行不同配比试验研究.
2.3 配比试验设计与结果充填材料配比的优劣往往通过充填性能参数来评价,如充填体强度、料浆流动特性、泌水性能、充填成本和充填工艺操作难易程度等,相应的影响因素有尾砂成分、密度、级配、胶凝材料类别、料浆质量浓度、砂灰质量比、温度、制浆水性质和添加剂类别等[18-20],受实际工程制约,有些影响因素水平是固定的.对此,本文重点研究制浆水性x1、砂灰质量比x2和料浆质量浓度x33个影响因素对充填体强度(28 d)Y1、塌落度Y2和体积泌水率(90 min)Y3 3个目标的影响规律.由于Box-Behnken方法在实验设计中没有加入轴向点,同比中心组合实验的次数较少.因此,本文采用Box-Behnken设计开展实验,根据设计原理进行3因素3水平设计,影响因素及水平见表 2.表中,中心水平为基准组,编码值根据式(8)计算:
| 表 2 响应量影响因素及水平 Table 2 Factors and levels of response variables |
| $ {X_i} = \left( {{x_i} - {x_0}} \right)/\Delta x. $ | (8) |
式中:Xi为自变量xi的编码值,x0为自变量在中心点的值,Δxi为自变量变化步长.
为考察海水对充填性能的影响,试验采用自来水、混合水(海水和自来水按质量比1:1混合)和海水作为制浆水性的3个水平,编码值分别为-1、0和1;砂灰比3水平为4:1、10:1和16:1;考虑到测得尾砂的最大沉降质量浓度为79.1%,料浆质量浓度的3个水平设计为68%、70%和72%.本次研究共开展13组试验,料浆制备后先测量坍落度和不同时间的泌水率,然后将其浇入7.07 cm×7.07 cm×7.07 cm标准三联试模,每组实验制作3件三联模,初凝后刮模、脱模将充填体置入HSB-40B型养护箱按照井下平均气候条件(温度20 ℃、湿度90%)进行养护,采用WHY-200万能压力试验机对不同龄期(7 d、14 d和28 d)充填体单轴抗压强度进行测试.根据实验方案测得不同配比的充填体强度、塌落度和泌水率见表 3,可见,料浆泌水率在料浆制备后0.5~1.0 h基本达到稳定.
| 表 3 不同充填材料配比试验结果 Table 3 Test results of different mix proportioning of filling materials |
根据不同配比试验结果,采用Design-expert软件按照式(1)~(4)拟合充填体影响因素与响应量的响应面函数:
| $ \begin{array}{l} {Y_1} = 0.05x_1^2 + 0.03x_2^2 - 0.01x_3^2 - 5 \times {10^{ - 3}}{x_1}{x_2} + \\ \;\;\;\;\;\;\;\;\;0.02{x_1}{x_3} - 8.54 \times {10^{ - 3}}{x_2}{x_3} - 1.08{x_1} - \\ \;\;\;\;\;\;\;\;\;0.35{x_2} + 1.63{x_3} - 56.70, \end{array} $ | (9) |
| $ \begin{array}{l} {Y_2} = - 0.68x_1^2 - 0.02x_2^2 + 0.05x_3^2 - 8.33 \times \\ \;\;\;\;\;\;\;\;\;\;{10^{ - 3}}{x_1}{x_2} - 0.09{x_1}{x_3} - 0.01{x_2}{x_3} + \\ \;\;\;\;\;\;\;\;\;\;6.10{x_1} + 1.21{x_2} - 7.28{x_3} + 290.64, \end{array} $ | (10) |
| $ \begin{array}{l} {Y_3} = 0.82x_1^2 + 3.89 \times {10^{ - 3}}x_2^2 + 0.29x_3^2 + 0.01{x_1}{x_2} + \\ \;\;\;\;\;\;\;\;0.03{x_1}{x_3} - 0.05{x_2}{x_3} - 1.86{x_1} + 3.43{x_2} - \\ \;\;\;\;\;\;\;\;41.10{x_3} + 1455.89. \end{array} $ | (11) |
3个响应面函数拟合的相关系数平方R2分别为0.997 6、0.905 0和0.998 9.对响应面回归模型进行方差分析,见表 4.其中,p>0.05表示该因素影响不显著,p<0.05表示该因素影响比较显著,p<0.000 1表示该因素影响极显著.
| 表 4 响应面回归模型方差分析 Table 4 Analysis of variance with the regression model of different response surfaces |
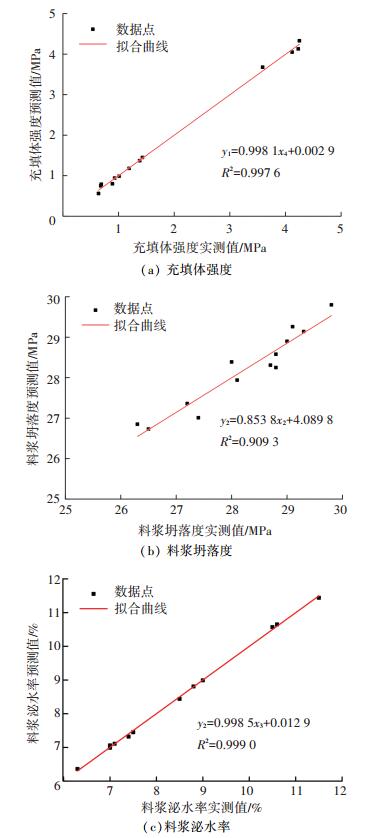
由表 4可知,塌落度拟合优度不及充填体强度和泌水率拟合优度,充填体强度、坍落度和泌水率拟合值和实际值的平均绝对误差分别为4.40%、1.28%、0.70%,见图 2,可见各响应面总体拟合较好,可靠度较高.
|
图 2 不同响应量预测值图和实测值对比 Figure 2 Comparison between predicted and measured values of different response variables |
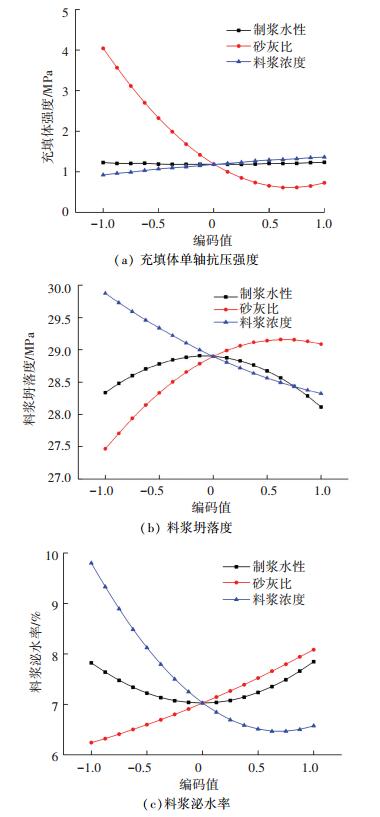
在充填体强度响应面回归模型中,充填体受到因素之间交互作用不显著,主要是受个别单因素制约.根据p值大小可知,制浆水性对充填体强度影响不显著.砂灰比对充填体强度影响极显著,随着砂灰比的增大,充填体强度逐渐降低,砂灰比在13:1以后,充填体强度变化不大.料浆质量浓度对充填体强度影响较显著,随着料浆质量浓度的增大,充填体强度稍微增大,但增幅不剧烈,主要是料浆质量浓度越高,泌水量越小,流失的C料越少,因而充填体强度会稍变大.充填体强度单因素影响曲线见图 3(a).
|
图 3 不同响应量单因素影响分析 Figure 3 Effect analysis of single factor on different response variables |
在坍落度响应面回归模型中,砂灰比和料浆质量浓度对坍落度的影响均较显著,且后者显著性程度高于前者,但两者之间交互作用不显著.制浆水性对坍落度影响无规律可循,影响程度不大;坍落度随着砂灰比增大逐渐增大,砂灰比小于10:1对坍落度影响较剧烈,大于10:1以后坍落度基本无变化;料浆质量浓度对塌落度影响最大,料浆质量浓度越大,塌落度越小,二者接近线性变化,见图 3(b).
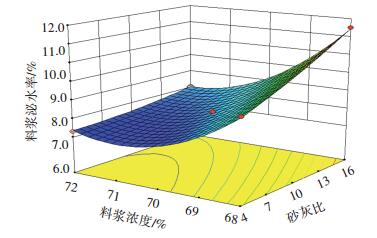
在泌水率响应面回归模型中,见图 3(c),制浆水性对料浆泌水性能影响不大,加之它对充填体强度、料浆坍落度都没有显著影响.可见,将海水用于充填制浆用水是科学合理的,可在具备条件的工程中推广应用.砂灰比和料浆质量浓度对泌水率的影响均极为显著,且二者之间存在极显著的交互作用.随着砂灰比的增大,泌水率随之增大,这主要是C料与水发生水化反应后包裹大量水分,C料越少,浸润粘附的水分越少,泌水量越大.此外,泌水率还受料浆质量浓度的极显著影响,二者呈反比例关系,显然这是和工程实际是相吻合的.从影响曲线还可看出,料浆质量浓度在71%~72%之间时,料浆泌水率基本无变化.砂灰比和和料浆质量浓度对泌水性能的交互作用响应面见图 4.随着质量浓度的升高,料浆泌水率显著下降;随着料浆砂灰比的增大,泌水率有显著增大的趋势.
|
图 4 砂灰比和料浆质量浓度对泌水率的交互作用 Figure 4 Interaction effect between tailings-to-cement ratio and slurry mass concentration on the bleeding rate |
根据满意度函数法原理,对充填材料配比进行优化要对响应量优化区间进行设定.对于充填体强度,若强度太大,成本太高会造成不必要的浪费;强度太小,则不能满足生产安全要求.目前,充填体强度主要采用Mitchell等、蔡嗣经和刘志祥等提出的公式进行设计,分别如下[21-23]:
| $ {\sigma _c} = \frac{{0.0098\rho HF}}{{\left( {\tan \beta + H/L} \right)}}, $ | (12) |
| $ {\sigma _c} = F\sqrt[3]{{{H^2}/a}}, $ | (13) |
| $ {\sigma _c} = \left( {5.085\lg \eta {\gamma ^2}{h^2}/{E_0} + 10.8154} \right)F. $ | (14) |
式中:σc为充填体长期强度,MPa;ρ为充填体密度,取2.1 t·m-3;H为充填体最大自立高度,取分段高10 m;h为埋深,取最大值385 m;L为充填体长度,取采场长度150 m;β为充填体底部滑动面与水平面夹角,大小为45°和内摩擦角一半之和,64.35°;F为安全系数,取2.2;a为经验系数,当H < 50 m时,a=600,H>100 m时,a=1 000;η为匹配系数,取5.28[23];γ为覆岩容重,取26.8 kN/m3;E0为围岩弹性模量,取50 GPa.
根据矿山开采技术条件按式(12)~(14)分别计算充填体临界强度为0.22 MPa、1.21 MPa和1.98 MPa.因此,设定充填体长期强度区间为0.5 MPa~4 MPa,设置目标值为1.98 MPa.料浆坍落度范围定义为15 cm~30 cm,根据Fall等[24]研究,料浆坍落度最优目标值为18 cm.根据充填体含水状态,泌水率区间为5%~20%,泌水率属于望小特性.采用层次分析法计算充填体强度、料浆坍落度和泌水率在充填性能中的权重向量为(0.5, 03, 0.2),因此,定义r1=5,r2=3,r3=2,根据式(5)、(6)可计算单指标满意度函数和整体满意度.
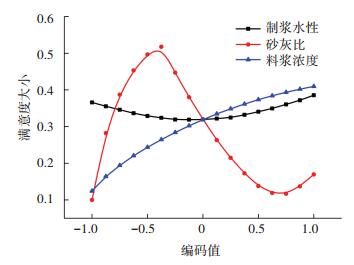
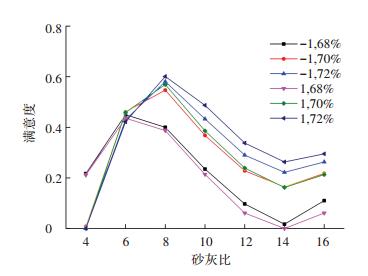
整体满意度单因素影响规律见图 5,由图可知,制浆水性对整体满意度作用不大,满意度介于0.3~0.4,这再次证实海水可作为充填水源.砂灰比在4:1~16:1范围内满意度先增大后降低,在8:1左右满意度最大,满意度达到0.5以上.料浆质量浓度对满意度影响也较为显著,质量浓度为72%对应的满意度为0.4,而质量浓度68%对应的满意度为0.1,工程中在满足输送工艺要求的条件下应尽可能提高充填料浆质量浓度.整体满意度多因素影响规律见图 6,可见,砂灰比在8:1左右、充填水性为1、料浆质量浓度为72%配比下的条件同比其他条件的整体满意度要高.软件拟合的最优充填配比为:制浆水性为海水,砂灰比为8.44:1,料浆质量浓度为72%,此时满意度最大(D=0.628),相应的响应量为:充填体强度2.00 MPa,料浆塌落度27.15 cm,料浆泌水率7.35%.
|
图 5 充填性能整体满意度的单因素影响 Figure 5 Effect of one factor on overall desirability of filling performance |
|
图 6 充填性能整体满意度的多因素影响 Figure 6 Effect of all factors on overall desirability of filling performance |
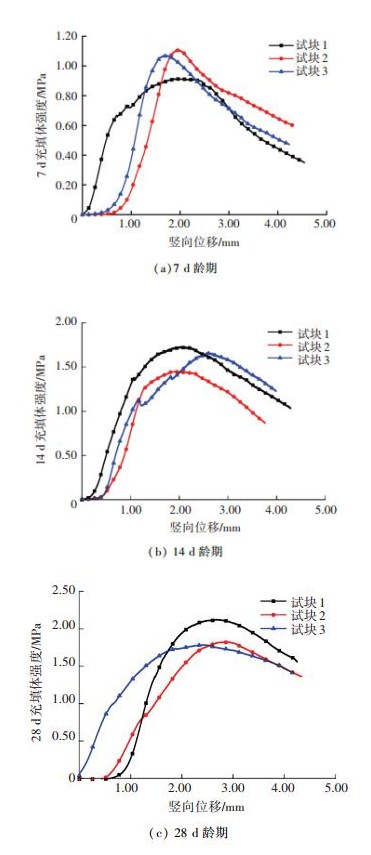
为验证响应面优化结果的可靠性,根据上述配比优化结果开展验证实验,测定相应的充填性能参数.实验充填材料总质量4 kg,其中尾砂257 4.92 g,C料305.08 g,海水112 0 g,按照步骤“搅拌-灌模-脱模-养护-测试”进行试验.实验结果为:料浆坍落度为26.92 cm;料浆泌水率为7.40%(90 min);7 d、14 d和28 d不同龄期充填体强度平均为0.98 MPa、1.61 MPa和1.91 MPa,见图 7.同时根据式(9)可计算7 d和14 d龄期充填体理论强度为1.08 MPa和1.66 MPa.可见,充填配比响应面优化结果和实验结论基本吻合,采用响应面-满意度函数法优化矿山充填材料配比是行之有效的.
|
图 7 不同龄期充填体单轴抗压强度 Figure 7 Uniaxial compressive strength of filling body at different curing time |
1) 海水对充填体强度、料浆坍落度和泌水率影响不显著,可作为尾砂胶结充填用水来源.
2) 砂灰比对充填体强度影响极显著;坍落度受料浆质量浓度、砂灰比影响较显著;砂灰比和料浆质量浓度及其交互作用对泌水率的影响均极为显著.尾砂胶结充填最优配比为:制浆水性为海水,砂灰比为8.44:01,料浆质量浓度为72%,相应的响应量预测结果为:充填强度2.00 MPa,料浆塌落度27.15 cm,料浆泌水率7.35%,与验证实验结果基本一致.
3) 需要说明的是,充填材料还包括减水剂、早凝剂、早强剂等各类添加剂,充填性能参数还包括扩散度、粘度、屈服应力、充填成本等等,今后研究将考虑更多影响因素和目标响应量以进一步提高本文结论的可靠度.
| [1] |
刘同有, 韩斌, 王小卫. 镍闪速炉水淬渣胶结充填配合比优化选择与分析[J].
中国矿业, 2000, 9(6): 19-22.
LIU Tongyou, HAN Bin, WANG Xiaowei. Utilization of nickel flash-smelting furnace slag as material for cemented stowing[J]. China Mine Magazine, 2000, 9(6): 19-22. |
| [2] |
周科平, 古德生. 安庆铜矿尾砂胶结充填灰砂配比的遗传优化设计[J].
金属矿山, 2001(7): 11-13.
ZHOU Keping, GU Desheng. Genetic optimization design of the cement-sand ratio of tailings consolidated filling in Anqing copper mine[J]. Metal Mine, 2001(7): 11-13. |
| [3] |
李夕兵, 刘志祥. 高阶段尾砂胶结充填体力学研究与博弈树配比优化[J].
安全与环境学报, 2004, 4(4): 87-90.
LI Xibing, LIU Zhixiang. On mechanics of high consolidated tailings backfill and cement-tailing ratios optimization with game tree[J]. Journal of Safety and Environment, 2004, 4(4): 87-90. |
| [4] |
王新民, 徐东升. 胶结充填料优化配比研究及强度预测[J].
现代矿业, 2006, 25(12): 20-23.
WANG Xinmin, XU Dongsheng. Research on optimization proportioning of cemented filling material and strength forecasting[J]. Modern Mining, 2006, 25(12): 20-23. |
| [5] |
CHANG Qingliang, ZHOU Huaqiang, HOU Chaojiong. Using particle swarm optimization algorithm in an artificial neutral network to forecast the strength of paste filling material[J].
Journal of China University of Mining and Technology, 2008, 18(4): 551-555.
DOI: 10.1016/S1006-1266(08)60292-8 |
| [6] |
张钦礼, 李谢平, 杨伟. 基于BP网络的某矿山充填料浆配比优化[J].
中南大学学报(自然科学版), 2013, 44(7): 2867-2874.
ZHANG Qinli, LI Xieping, YANG Wei. Optimization of filling slurry ratio in a mine based on back-propagation neural network[J]. Journal of Central South University (Science and Technology), 2013, 44(7): 2867-2874. |
| [7] |
艾纯明, 吴爱祥, 王洪江, 等. 泵送剂改善膏体输送性能及配比优化[J].
科技导报, 2016, 34(2): 210-214.
AI Chunming, WU Aixiang, WANG Hongjiang, et al. Optimization of mix proportion of paste based on uniform design[J]. Science & Technology Review, 2016, 34(2): 210-214. DOI: 10.3981/j.issn.1000-7857.2016.2.035 |
| [8] |
韩斌, 刘超, 孙伟, 等. 废石破碎胶结充填配比优选及在寒冷气候条件下的应用[J].
中南大学学报(自然科学版), 2015, 46(11): 4195-4203.
HAN Bin, LIU Chao, SUN Wei, et al. Optimized mix ratio of crushed waste rocks in cementing backfill and its application in extreme cold weatherk[J]. Journal of Central South University (Science and Technology), 2015, 46(11): 4195-4203. DOI: 10.11817/j.issn.1672-7207.2015.11.029 |
| [9] |
CUI Mingyi, HU Hua. Realizing of optimization of binder backfill material under certain strength with fuzzy sets[J].
Journal of China University of Mining and Technology, 2001, 11(2): 147-149.
|
| [10] |
FALL M, BENZAAZOUA M. Modeling the effect of sulphate on strength development of paste backfill and binder mixture optimization[J].
Cement and Concrete Research, 2005, 35(2): 301-314.
DOI: 10.1016/j.cemconres.2004.05.020 |
| [11] |
LIU Zhixiang, DANG Wengang, LIU Qingling, et al. Optimization of clay material mixture ratio and filling process in gypsum mine goaf[J].
International Journal of Mining Science and Technology, 2013, 23(3): 337-342.
DOI: 10.1016/j.ijmst.2013.05.018 |
| [12] |
谢广祥. 巷旁充填材料的优化选择[J].
矿山压力与顶板管理, 1995(1): 49-52.
XIE Guangxiang. Optimization of filling materials next to roadway[J]. Ground Pressure and Strata Control, 1995(1): 49-52. |
| [13] |
刘浪. 矿山充填膏体配比优化与流动特性研究[D]. 长沙: 中南大学, 2013.
LIU Lang. Research on proportion optimization and flow characteristic of backfill paste in mine sites[D]. Changsha: Central South University, 2013. |
| [14] |
李典, 冯国瑞, 郭玉霞, 等. 基于响应面法的充填体强度增长规律分析[J].
煤炭学报, 2016, 41(2): 392-398.
LI Dian, FENG Guorui, GUO Yuxia, et al. Analysis on the strength increase law of filling material based on response surface method[J]. Journal of China Society, 2016, 41(2): 392-398. |
| [15] |
CANDIOTI L V, DE ZAN M M, CAMARA M S, et al. Experimental design and multiple response optimization. Using the desirability function in analytical methods development[J].
Talanta, 2014, 124(124): 123-138.
|
| [16] |
BOX G E P, WILSON K G. On the experimental attainment of optimum conditions[J].
Journal of Royal Statistics Society, 1951, 23(1): 1-45.
|
| [17] |
GEORGE D, RONALD S. Simultaneous optimization of several response variables[J].
Journal of quality technology, 1980, 12(4): 214-219.
|
| [18] |
赵国彦, 马举, 彭康, 等. 基于响应面法的高寒矿山充填配比优化[J].
北京科技大学学报, 2013, 35(5): 559-565.
ZHAO Guoyan, MA Ju, PENG Kang, et al. Mix ratio optimization of alpine mine backfill based on the response surface method[J]. Journal of University of Science and Technology Beijing, 2013, 35(5): 559-565. |
| [19] |
KESIMAL A, YILMAZ B, ERCIKDI B, et al. Effect of properties of tailings and binder on the short-and long-term strength and stability of cemented paste backfill[J].
Materials Letters, 2005, 59(28): 3703-3709.
DOI: 10.1016/j.matlet.2005.06.042 |
| [20] |
ALDHAFEERI Z, FALL M, POKHAREL M, et al. Temperature dependence of the reactivity of cemented paste backfill[J].
Applied Geochemistry, 2016, 72(9): 10-19.
|
| [21] |
MITCHELL R J, OLSEN R S, SMITH J D. Model studies on cemented tailings used in mine backfill[J].
Canadian Geotechnical Journal, 1982, 19(1): 14-28.
DOI: 10.1139/t82-002 |
| [22] |
蔡嗣经.
矿山充填力学基础[M]. 2版. 北京: 冶金工业出版社, 2009: 188-194.
CAI Sijing. Foundation of mine filling mechanics[M]. 2th ed. Beijing: Metallurgical Industry Press, 2009: 188-194. |
| [23] |
刘志祥, 李夕兵, 戴塔根, 等. 尾砂胶结充填体损伤模型及与岩体的匹配分析[J].
岩土力学, 2006, 27(9): 1442-1446.
LIU Zhixiang, LI Xibing, DAI Tagen, et al. On damage model of cemented tailings backfill and its match with rock mass[J]. Rock and Soil Mechanics, 2006, 27(9): 1442-1446. |
| [24] |
FALL M, BENZAAZOUA M, SAA E G. Mix proportioning of underground cemented tailings backfill[J].
Tunnelling and Underground Space Technology, 2008, 23(1): 80-90.
DOI: 10.1016/j.tust.2006.08.005 |
 2017, Vol. 49
2017, Vol. 49


