载波相位观测量因其高精度被广泛应用在全球卫星导航系统(Global Navigation Satellite System, GNSS)中,但只有当准确解算出整周模糊度,利用载波相位观测量进行定位才变得有意义.差分定位原理主要依靠载波相位和伪距双差可以消除相关误差,但当接收机间距离超过10 km时,该误差处理策略失效[1].随距离增加的大气层延迟误差残差及缺乏足够的数据冗余度去解决整周模糊度是制约其基线长度的一个重要因素[2].对于中长基线,电离层与对流层在经过站间、星间双差后的残差都应该作为一未知参数被考虑[3],但这会加重整周模糊度求解模型的病态性,造成模糊度固定失败.卡尔加里大学利用几种观测量线性组合包括双差宽巷组合和电离层无关线性组合及卡尔加里大学提出的模型,消除电离层和对流层误差对中长基线下整周模糊度求解的影响[4];部分学者利用三频观测数据,通过电离层无关组合消除电离层延迟误差对整周模糊度求解的影响[5-7];除了上述方法还可以利用Thai电离层地图解决RTK中模型中电离层误差问题[8];对于对流层误差,最常用的方法是通过经验模型求解,弗罗茨瓦夫大学针对波兰地区研究了两种对流层延迟误差模型,并对其在单基线和多基线场景下的精度进行了研究分析[9];对于快速精密定位常见的有两种对流层延迟估计模型[10];近些年来,随着CORS系统等地面基站的建设,多基站辅助解决大气误差策略应运而生,利用网络基站通过插值得到网络电离层延迟修正量[11],但插值过程的误差是不可避免的,因此发展了一系列方法,如对天顶对流层参数限制提出一种正则化方法[12],利用经验对流层模型GT2生成一个高精度的有先验参数的对流层延迟,改善传统网络RTK模型中整周模糊度求解方程的病态性;利用2个基站对用户进行相对精密定位[13],其中一个基站离用户基站非常近,可以看做零基线,其中零基线的基站跟用户站有着相似的电离层及对流层延迟.将已知基线长度、不同基线之间整周模糊度的关系以及相似的电离层对流层延迟等已知条件充分应用到相对精密定位中,改善整周模糊度的固定情况以及最终的定位精度;科廷大学提出了利用多系统提高中长基线整周模糊度固定率的方法[14-15],更多利用多系统组合数据提高精密定位精度的研究见文献[16-18].
为满足单一系统,没有足够的观测网络数据情况时的实时定位需求,本文提出了单系统、单基线条件下的一种双频非组合实时精密定位技术,采用双频双差模型,消除卫星钟差和接收机钟差等与距离无关的相关误差的影响,同时减弱诸如轨道误差、大气折射误差等系统性误差的影响,对于对流层延迟误差,本文利用Saastamoinen模型估计后对原始观测量进行补偿,对于影响整周模糊度解算的主要误差电离层双差误差则设为未知参数,最后通过扩展卡尔曼滤波器进行用户位置求解.文中单独处理两频率上的观测量数据,有效避免了观测值组合过程所引起的观测噪声.
1 数学模型 1.1 双频双差基础模型| $ \begin{array}{l} \mathit{\Phi }_{1,{\rm{ur}}}^{ij} = \rho _{{\rm{ur}}}^{ij} + \delta \rho _{{\rm{ur}}}^{ij} + T_{{\rm{ur}}}^{ij} - I_{{\rm{ur}}}^{ij} + {\lambda _1}N_{1,{\rm{ur}}}^{ij} + M_{\mathit{\Phi }1,{\rm{ur}}}^{ij} + \\ \;\;\;\;\;\;\;\;\;\;\;\varepsilon _{\mathit{\Phi }1,{\rm{ur}}}^{ij} \end{array} $ |
| $ \begin{array}{l} \mathit{\Phi }_{2,{\rm{ur}}}^{ij} = \rho _{{\rm{ur}}}^{ij} + \delta \rho _{{\rm{ur}}}^{ij} + T_{{\rm{ur}}}^{ij} - \left( {f_1^2/f_2^2} \right)I_{{\rm{ur}}}^{ij} + {\lambda _2}N_{2,{\rm{ur}}}^{ij} + \\ \;\;\;\;\;\;\;\;\;\;\;M_{\mathit{\Phi }1,{\rm{ur}}}^{ij} + \varepsilon _{\mathit{\Phi }2,{\rm{ur}}}^{ij} \end{array} $ |
| $ P_{1,{\rm{ur}}}^{ij} = \rho _{{\rm{ur}}}^{ij} + \delta \rho _{{\rm{ur}}}^{ij} + T_{{\rm{ur}}}^{ij} + I_{{\rm{ur}}}^{ij} + M_{\mathit{P}1,{\rm{ur}}}^{ij} + \varepsilon _{\mathit{P}1,{\rm{ur}}}^{ij} $ |
| $ \begin{array}{l} P_{2,{\rm{ur}}}^{ij} = \rho _{{\rm{ur}}}^{ij} + \delta \rho _{{\rm{ur}}}^{ij} + T_{{\rm{ur}}}^{ij} + \left( {f_1^2/f_2^2} \right)I_{{\rm{ur}}}^{ij} + M_{\mathit{P}2,{\rm{ur}}}^{ij} + \\ \;\;\;\;\;\;\;\;\;\;\varepsilon _{\text{P}2,{\rm{ur}}}^{ij}. \end{array} $ | (1) |
式(1)为双频双差的基础模型,其中,i,j为卫星号,u,r分别代表用户和基准站,Φn, urij,Pn, urij分别为频率n上的双差载波相位观测量和双差码观测量,ρurij为卫星到用户和基站间几何距离的双差观测量,δρurij为卫星轨道误差造成的距离误差双差,Turij为双差对流层延迟误差,Iurij为双差电离层延迟误差,f1,f2分别为载波L1及L2频率,λ1,λ2分别为载波L1及L2波长,N1, urij,N2, urij为载波L1及L2的双差整周模糊度,MΦ, urij,MP, urij分别为载波相位观测量和伪距观测量对应的双差后的多径误差.站间-星间双差的应用,有效减少了定位模型未知数的个数,而双频数据的应用则有效提高了观测量的冗余度,为单历元单基线精密定位提供了基础保障.
1.2 误差处理策略高精度RTK定位主要依据载波相位观测量,为提高整周模糊度解算的准确性,必须设法解决式(1)中影响定位结果的各个误差.对于短基线而言,在经过站间及星间双差后,认为消除或近似消除了卫星钟差、接收机钟差、轨道误差、对流层延迟误差、电离层延迟误差等,但如果用户和基站间基线长度超过10 km,有些误差经过双差后的残差需要分析、考虑,尤其是与距离相关的一些误差,如电离层误差、对流层误差及卫星轨道误差,本文的误差处理策略主要考虑了这三种误差的处理方法.
1.2.1 卫星轨道误差卫星轨道误差对最终定位结果的影响随基线长度的增加而增加见下式.
| $ \left| {\frac{{{\rm{d}}b}}{b}} \right| = \left| {\frac{{{\rm{d}}\rho }}{\rho }} \right|. $ | (2) |
式中: dρ为卫星轨道误差,ρ为卫星与接收机间距离,db为因卫星轨道误差对用户定位结果造成的误差,b为基线长度.卫星到接收机间的距离大约为20 000 km,而中长基线的基线长度从10~300 km间不等.对于卫星轨道误差,有些单位提供了不同精度的轨道产品,对于IGS产品的精度如表 1[19].
| 表 1 IGS产品精度表 Table 1 The precision of IGS products |
根据表 1和式(2),在相对定位中采用广播星历时,由卫星轨道误差造成的定位误差在基线长度小于200 km时,不足1 cm,此时,卫星轨道误差可以忽略;当基线长度为300 km时,定位误差则为1.5 cm,此时可以采用卫星轨道改进方法,进一步减少卫星星历误差.本文中,用户与基站的距离小200 km,因此忽略卫星轨道误差及由其引起的距离误差双差δρurij.
1.2.2 对流层延迟误差对流层天顶延迟总量由90%的干延迟分量和10%的湿延迟分量构成[20],对流层延迟误差通常表示为天顶方向的对流层折射量与仰角的映射函数之积,如式
| $ T\left( e \right) = mh\left( e \right) \times zh + mw\left( e \right) \times zw. $ | (3) |
式中: e为天顶角,zh, zw分别为对流层的干湿分量,mh, mw分别为干湿分量的仰角映射函数.关于对流层天顶延迟量相关模型,见参考文献[21-23].
对于基线长度超过50 km的用户,应将双差对流层残余作为未知参数考虑,但这会加重整周模糊度求解模型的病态性[12].因此对于对流层延迟本文采用模型估计方法,尽量降低对流层延迟的误差干扰.对流层天顶延迟量采用Saastamoinen模型估计[24],得到对流层天顶延迟的干延迟分量和由水蒸气引起的湿延迟分量,映射函数采用GMF[25].对于对流层延迟误差,本文直接在原始观测量上进行补偿,从而降低定位模型中的未知参数个数,增加模型方程观测量冗余度.
1.2.3 电离层延迟误差电离层延迟误差是影响用户定位的主要误差源之一,不同测站的电离层延迟误差不同,同一测站不同观测方向上的电离层延迟误差也不同.一般对于短基线用户而言,其电离层误差与基站误差近似认为相等,因此可以通过差分技术消除,但当用户基线超过10 km后,电离层差分残余误差将对定位结果造成较大误差.
为了消除中长基线的电离层延迟误差,许多学者提出了利用电离层无关组合消除电离层延迟误差,但双频电离层无关组合会使得测量噪声增加,由误差传播定律,伪距观测量的无电离层组合观测值的观测噪声为单频率上双差伪距噪声的2.978倍[26],并且因为组合观测量的波长太短,造成短时间内模糊度固定困难[27],因此该方法大部分基于网络基站或三频数据条件下[4-7].针对单基线单系统双频数据条件下中长基线的实时精密定位,本文将电离层延迟站间-星间双差残差值设为未知参数,假设用户和接收机在频率fn(n=1, 2)上同时观测到m颗卫星,则选定参考星后,对电离层延迟误差做站间-星间差分处理,得到m-1个双差电离层延迟量作为扩展卡尔曼的未知状态向量求解.
1.2.4 多径误差由公式(1),除了卫星轨道误差、对流层延迟误差、电离层延迟误差,用户在进行了站间-星间双差后,还存在多径误差.本文中对多径误差不作重点研究,假设接收机处于空旷区域,因此对于文中所提的双频非组合实时精密定位方法,从建模到利用实际数据进行验证,均没有考虑多径误差.
1.3 单基线双频非组合模型 1.3.1 EKF建模及求解EKF是通过线性化处理来实现非线性滤波估计,是用高斯分布来逼近系统状态的后验概率密度.相对于处理非线性滤波的粒子波波器等,在计算速度上,EKF具有明显的优势.本文采用EKF对式(1)中的双频双差模型进行求解,首先利用泰勒展开式对非线性函数进行线性化处理,然后再在标准卡尔曼滤波框架下进行递归滤波,包括测量更新和时间更新两个过程.线性化后的双差非组合定位的状态预测方程和测量方程如式:
| $ {\mathit{\boldsymbol{X}}_k} = {\mathit{\boldsymbol{F}}_{k,k - 1}}{\mathit{\boldsymbol{X}}_{k - 1}} + {\mathit{\boldsymbol{W}}_k}, $ | (4) |
| $ {\mathit{\boldsymbol{y}}_k} = {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{X}}_k} + {\mathit{\boldsymbol{e}}_k}. $ | (5) |
式中: Xk为k时刻状态向量,yk为k时刻观测值,Fk, k-1为第k-1时刻到k时刻的状态转移矩阵,Wk为状态模型噪声,ek为测量噪声,假设状态模型噪声Wk和测量噪声ek互为不相关的白噪声序列,其协方差矩阵分别为Qw和Re.假设1号卫星为选定的参考卫星,则未知状态向量Xk为
| $ {\mathit{\boldsymbol{X}}_k} = {\left[ {{r_x},{r_y},{r_z},{\nu _x},{\nu _y},{\nu _z},I_{{\rm{ur}}}^{12}, \cdots ,I_{{\rm{ur}}}^{1m},N_{1,{\rm{ur}}}^{12}, \cdots ,N_{2,{\rm{ur}}}^{1m}} \right]^{\rm{T}}}. $ | (6) |
式中:rx, ry, rz为WGS-84坐标系下x, y, z三轴位置参数,νx, νy, νz为相应的三轴速度参数,Iur12, …, Iur1m为电离层延迟双差值,Nn, ur12, …, Nn, ur1m为频率n上的整周模糊度双差值.观测向量y如式
| $ {\mathit{\boldsymbol{y}}_k} = {\left( {\nabla \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_1^{\rm{T}},\nabla \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_2^{\rm{T}},\nabla \mathit{\boldsymbol{P}}_1^{\rm{T}},\nabla \mathit{\boldsymbol{P}}_2^{\rm{T}}} \right)^{\rm{T}}}. $ | (7) |
其中:
| $ \begin{array}{l} \nabla {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_n} = {\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{n,{\rm{ur}}}^{12},\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{n,{\rm{ur}}}^{13}, \cdots ,\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{n,{\rm{ur}}}^{1m}} \right)^{\rm{T}}},n = 1,2;\\ \nabla {\mathit{\boldsymbol{P}}_n} = {\left( {\mathit{\boldsymbol{P}}_{n,{\rm{ur}}}^{12},\mathit{\boldsymbol{P}}_{n,{\rm{ur}}}^{13}, \cdots ,\mathit{\boldsymbol{P}}_{n,{\rm{ur}}}^{1m}} \right)^{\rm{T}}},n = 1,2. \end{array} $ | (8) |
测量模型向量b(x)、观测矩阵Hg为:
| $ \mathit{\boldsymbol{b}}\left( x \right) = {\left( {\mathit{\boldsymbol{b}}_{\Phi ,1}^{\rm{T}},\mathit{\boldsymbol{b}}_{\Phi ,2}^{\rm{T}},\mathit{\boldsymbol{b}}_{{\rm{P}},1}^{\rm{T}},\mathit{\boldsymbol{b}}_{{\rm{P}},2}^{\rm{T}}} \right)^{\rm{T}}}. $ | (9) |
| $ {\mathit{\boldsymbol{b}}_{\Phi ,n}} = \left[ {\begin{array}{*{20}{c}} {\rho _{{\rm{ur}}}^{12} + {\mu _n}I_{{\rm{ur}}}^{12} + {\lambda _n}N_{n{\rm{,ur}}}^{12}}\\ {\rho _{{\rm{ur}}}^{13} + {\mu _n}I_{{\rm{ur}}}^{13} + {\lambda _n}N_{n{\rm{,ur}}}^{13}}\\ \vdots \\ {\rho _{{\rm{ur}}}^{1m} + {\mu _n}I_{{\rm{ur}}}^{1m} + {\lambda _n}N_{n{\rm{,ur}}}^{1m}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{b}}_{{\rm{P}},n}} = \left[ {\begin{array}{*{20}{c}} {\rho _{{\rm{ur}}}^{12} - {\mu _n}I_{{\rm{ur}}}^{12}}\\ {\rho _{{\rm{ur}}}^{13} - {\mu _n}I_{{\rm{ur}}}^{13}}\\ \vdots \\ {\rho _{{\rm{ur}}}^{1m} + {\mu _n}I_{{\rm{ur}}}^{1m}} \end{array}} \right],{\mathit{\boldsymbol{\mu }}_n} = \left[ {1,\frac{{f_1^2}}{{f_2^2}}} \right], $ | (10) |
| $ {\mathit{\boldsymbol{H}}_g} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{S}}_{\rm{s}}}{\mathit{\boldsymbol{G}}_{\rm{g}}}}&\mathit{\boldsymbol{0}}&{{\mu _1}\mathit{\boldsymbol{E}}}&{{\lambda _1}{\mathit{\boldsymbol{E}}_0}}&\mathit{\boldsymbol{0}}\\ {{\mathit{\boldsymbol{S}}_{\rm{s}}}{\mathit{\boldsymbol{G}}_{\rm{g}}}}&\mathit{\boldsymbol{0}}&{{\mu _2}\mathit{\boldsymbol{E}}}&\mathit{\boldsymbol{0}}&{{\lambda _2}{\mathit{\boldsymbol{E}}_0}}\\ {{\mathit{\boldsymbol{S}}_{\rm{s}}}{\mathit{\boldsymbol{G}}_{\rm{g}}}}&\mathit{\boldsymbol{0}}&{ - {\mu _1}\mathit{\boldsymbol{E}}}&\mathit{\boldsymbol{0}}&\mathit{\boldsymbol{0}}\\ {{\mathit{\boldsymbol{S}}_{\rm{s}}}{\mathit{\boldsymbol{G}}_{\rm{g}}}}&\mathit{\boldsymbol{0}}&{ - {\mu _2}\mathit{\boldsymbol{E}}}&\mathit{\boldsymbol{0}}&\mathit{\boldsymbol{0}} \end{array}} \right]. $ | (11) |
其中: Ss为星间单差矩阵,Gg为用户-卫星方向余弦向量,E0为单位矩阵,具体如式(12)到式(15).
| $ {\mathit{\boldsymbol{S}}_{\rm{s}}} = \left[ {\begin{array}{*{20}{c}} { - 1}&1&0& \cdots &0\\ { - 1}&0&1& \cdots &0\\ \vdots&\vdots&\vdots&\vdots&\vdots \\ { - 1}&0&0& \cdots &0 \end{array}} \right], $ | (12) |
| $ \begin{array}{l} {\mathit{\boldsymbol{G}}_{\rm{g}}} = {\left( {\mathit{\boldsymbol{e}}_{\rm{u}}^1,\mathit{\boldsymbol{e}}_{\rm{u}}^2, \cdots ,\mathit{\boldsymbol{e}}_{\rm{u}}^m} \right)^{\rm{T}}} = \\ \;\;\;\;\;\;\;\;{\left[ {\begin{array}{*{20}{c}} {\frac{{\widehat {{x_{\rm{u}}}} - {x^1}}}{{\widehat {\rho _{\rm{u}}^1}}}}&{\frac{{\widehat {{y_{\rm{u}}}} - {y^1}}}{{\widehat {\rho _{\rm{u}}^1}}}}&{\frac{{\widehat {{{\rm{z}}_{\rm{u}}}} - {z^1}}}{{\widehat {\rho _{\rm{u}}^1}}}}\\ {\frac{{\widehat {{x_{\rm{u}}}} - {x^2}}}{{\widehat {\rho _{\rm{u}}^2}}}}&{\frac{{\widehat {{y_{\rm{u}}}} - {y^2}}}{{\widehat {\rho _{\rm{u}}^2}}}}&{\frac{{\widehat {{{\rm{z}}_{\rm{u}}}} - {z^2}}}{{\widehat {\rho _{\rm{u}}^2}}}}\\ \vdots&\vdots&\vdots \\ {\frac{{\widehat {{x_{\rm{u}}}} - {x^m}}}{{\widehat {\rho _{\rm{u}}^m}}}}&{\frac{{\widehat {{y_{\rm{u}}}} - {y^m}}}{{\widehat {\rho _{\rm{u}}^m}}}}&{\frac{{\widehat {{{\rm{z}}_{\rm{u}}}} - {z^m}}}{{\widehat {\rho _{\rm{u}}^m}}}} \end{array}} \right]^{\rm{T}}}, \end{array} $ | (13) |
| $ \widehat {\rho _{\rm{u}}^{\rm{i}}} = \sqrt {{{\left( {\widehat {{x_{\rm{u}}}} - {x^{\rm{i}}}} \right)}^2} + {{\left( {\widehat {{y_{\rm{u}}}} - {y^{\rm{i}}}} \right)}^2} + {{\left( {\widehat {{z_{\rm{u}}}} - {z^{\rm{i}}}} \right)}^2}} , $ | (14) |
| $ {\mathit{\boldsymbol{E}}_0} = \left[ {\begin{array}{*{20}{c}} 1&0& \cdots &0\\ 0&1& \cdots &0\\ \vdots&\vdots&\vdots&\vdots \\ 0&0& \cdots &1 \end{array}} \right]. $ | (15) |
测量误差协方差矩阵Re描述测量过程中的误差,具体如式
| $ {\mathit{\boldsymbol{R}}_{\rm{e}}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{D}}{\mathit{\boldsymbol{R}}_{\mathit{\Phi },1}}{\mathit{\boldsymbol{D}}^{\rm{T}}}}&\mathit{\boldsymbol{0}}& \cdots &\mathit{\boldsymbol{0}}\\ \mathit{\boldsymbol{0}}&{\mathit{\boldsymbol{D}}{\mathit{\boldsymbol{R}}_{\mathit{\Phi },2}}{\mathit{\boldsymbol{D}}^{\rm{T}}}}& \cdots &\mathit{\boldsymbol{0}}\\ \vdots&\vdots &{\mathit{\boldsymbol{D}}{\mathit{\boldsymbol{R}}_{\mathit{P},1}}{\mathit{\boldsymbol{D}}^{\rm{T}}}}& \vdots \\ \mathit{\boldsymbol{0}}&\mathit{\boldsymbol{0}}& \cdots &{\mathit{\boldsymbol{D}}{\mathit{\boldsymbol{R}}_{\mathit{P},2}}{\mathit{\boldsymbol{D}}^{\rm{T}}}} \end{array}} \right]. $ | (16) |
其中: D为站间-星间双差矩阵,RΦ, n为频率n上的非差相位观测值的协方差矩阵,RP, n为频率n上的非差伪距观测值的协方差矩阵.
利用第k-1个历元的得到的状态向量对应的方差协方差矩阵P及过程噪声协方差矩阵计算第k个历元的状态向量对应的协方差矩阵,计算求得卡尔曼滤波器增益K,进而得到状态向量在第k个历元的的预测结果,如式:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat X}}}_k} = {{\mathit{\boldsymbol{\hat X}}}_{k,k - 1}} + {\mathit{\boldsymbol{K}}_k}\left( {{\mathit{\boldsymbol{y}}_k} - \mathit{\boldsymbol{b}}\left( {{{\mathit{\boldsymbol{\hat X}}}_{k,k - 1}}} \right)} \right)}\\ {{\mathit{\boldsymbol{P}}_k} = \left( {\mathit{\boldsymbol{E}} - {\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{H}}_{{\rm{g}},k}}} \right){\mathit{\boldsymbol{P}}_{k,k - 1}}}\\ {{\mathit{\boldsymbol{K}}_k} = {\mathit{\boldsymbol{P}}_{k,k - 1}}\mathit{\boldsymbol{H}}_{{\rm{g}},k}^{\rm{T}}{{\left( {{\mathit{\boldsymbol{H}}_{{\rm{g}},k}}{\mathit{\boldsymbol{P}}_{k,k - 1}}\mathit{\boldsymbol{H}}_{{\rm{g}},k}^{\rm{T}} + {\mathit{\boldsymbol{R}}_{{\rm{e}},k}}} \right)}^{ - 1}}} \end{array} $ | (17) |
式(17)为标准卡尔曼滤波器的测量更新过程.再按式(18)进行时间更新过程,为第k-1个历元求解做准备.
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat X}}}_{k + 1,k}} = \mathit{\boldsymbol{F}}_k^{k + 1}{{\mathit{\boldsymbol{\hat X}}}_k}}\\ {{\mathit{\boldsymbol{P}}_{k + 1,k}} = \mathit{\boldsymbol{F}}_k^{k + 1}{\mathit{\boldsymbol{P}}_k}\mathit{\boldsymbol{F}}_k^{k + 1,{\rm{T}}} + \mathit{\boldsymbol{Q}}_{{\rm{w}},k}^{k + 1},} \end{array} $ | (18) |
其中:
| $ {\mathit{\boldsymbol{F}}_k} = \left[ {\begin{array}{*{20}{c}} 1&0&0&\tau &0&0& \cdots &0\\ 0&1&0&0&\tau &0& \cdots &0\\ 0&0&1&0&0&\tau&\cdots &0\\ 0&0&0&1&0&0& \cdots &0\\ 0&0&0&0&1&0& \cdots &0\\ 0&0&0&0&0&1& \cdots &0\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots \\ 0&0&0&0&0&0& \cdots &1 \end{array}} \right], $ | (19) |
| $ {\mathit{\boldsymbol{Q}}_{\rm{w}}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{q}}_r}}&\mathit{\boldsymbol{0}}&\mathit{\boldsymbol{0}}&\mathit{\boldsymbol{0}}\\ \mathit{\boldsymbol{0}}&{{\mathit{\boldsymbol{q}}_v}}&\mathit{\boldsymbol{0}}&\mathit{\boldsymbol{0}}\\ \mathit{\boldsymbol{0}}&\mathit{\boldsymbol{0}}&{{\mathit{\boldsymbol{q}}_{\rm{I}}}}&\mathit{\boldsymbol{0}}\\ \mathit{\boldsymbol{0}}&\mathit{\boldsymbol{0}}&\mathit{\boldsymbol{0}}&{{\mathit{\boldsymbol{q}}_{\rm{N}}}} \end{array}} \right]. $ | (20) |
式中:τ为相邻两历元间的时间间隔,qr、qν、qI、qN分别为位置、速度、电离层延迟及整周模糊度的过程噪声协方差矩阵,共同构成矩阵过程噪声方差协方差矩阵Qw.为了避免因过度依赖模型而造成的滤波结果发散现象,利用Qw矩阵调节状态协方差矩阵P,避免P变得太小或者为0而导致的滤波器失效.根据卡尔曼滤波原理,最终的滤波结果是由模型状态预测值及观测值进行加权更新得到的,如果观测精度较高,则增加其权重,使得滤波结果倾向于观测结果,如果观测精度较低,则增加状态预测值对滤波结果的贡献.
在利用EKF得到L1及L2两个频率上的双差整周模糊度的浮点解及其方差协方差矩阵后,利用LAMBDA算法进行双差整周模糊度的固定,得到用户最后定位结果,关于LAMBDA算法具体见文献[28-29].
1.3.2 状态向量变换矩阵状态向量变换矩阵是指状态向量由上个历元到本历元的转换矩阵.在实际的定位解算过程中,由于时间或空间上的差异,会导致基准站与用户端观测到的公共卫星减少或增加,从而使实时整周模糊度向量与上个历元的双差模糊度解向量N1, ur12, …, N2, ur1m不一致,为了确保滤波的连续性和传递的准确性,需要根据共视卫星的变化情况,对电离层及模糊度向量进行相应更新.共视卫星的变化情况主要分为两种:
1) 参考卫星不变,其它共视卫星增加或减少.如果当前历元丢失非参考星,则将该卫星对应的整周模糊度项及电离层延迟项去掉,同时需去掉对应状态向量方差协方差矩阵P的相关行和列;如果当前历元增加非参考星,则构建该非参考星的站间-星间双差载波相位观测量,利用原有的已知双差模糊度向量及相应卫星的观测量,求出该时刻的基线向量,进而求得新增卫星的双差模糊度向量,如公式(21),或者直接利用其伪距和载波相位观测量,初始化其双差模糊度向量,如公式(22),对于双差电离层延迟项,则直接赋予其0的初值,同时将方差协方差矩阵P相关行和列元素置为0,如式(23).
| $ \nabla {\mathit{\boldsymbol{N}}_{{\rm{new}}}} = {\mathit{\boldsymbol{H}}_{{\rm{new}}}}{\mathit{\boldsymbol{b}}_{{\rm{ur}}}} - {\mathit{\boldsymbol{y}}_{\mathit{\Phi ,}{\rm{new}}}}, $ | (21) |
| $ \nabla {\mathit{\boldsymbol{N}}_{{\rm{new}}}} = \left( {\nabla {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{n,{\rm{new}}}} - \nabla {\mathit{\boldsymbol{P}}_{n,{\rm{new}}}}} \right)/\lambda ,\lambda = \left[ {{\lambda _1},{\lambda _2}} \right], $ | (22) |
| $ \nabla {\mathit{\boldsymbol{I}}_{{\rm{new}}}} = 0. $ | (23) |
2) 参考星改变.新历元数据在解算前,需要检测参考卫星较上个历元是否发生变换,若依据高度角最大原则,假设第k+1个历元参考星发生了变化,则需要变换矩阵Tk, N将第k个历元中以参考星p得到的双差模糊度解向量映射至新参考卫星pnew,具体如公式(24),对于双差电离层延迟项,利用变换矩阵Tk, I将第k个历元中以参考星p得到的双差电离层延迟量映射至新参考卫星pnew,如式(25),其中,Tk, N和Tk, I为单位阵对应新参考卫星的列统一减去1得到,由对应状态向量中的位置、速度形成的单位阵,结合Tk, N和Tk, I共同构成从第k个历元到第k+1个历元的状态解向量的变换矩阵Tk, 根据Tk,利用对第k+1个历元对应的状态向量方差协方差矩阵Pk+1, N, new进行更新,具体如式子(26).
| $ \nabla {\mathit{\boldsymbol{N}}_{k + 1,{\rm{new}}}} = {\mathit{\boldsymbol{T}}_{k,{\rm{N}}}}\nabla {\mathit{\boldsymbol{N}}_k}, $ | (24) |
| $ \nabla {\mathit{\boldsymbol{I}}_{k + 1,{\rm{new}}}} = {\mathit{\boldsymbol{T}}_{k,{\rm{I}}}}\nabla {\mathit{\boldsymbol{I}}_k}, $ | (25) |
| $ \nabla {\mathit{\boldsymbol{P}}_{k + 1,\mathit{I},{\rm{new}}}} = {\mathit{\boldsymbol{T}}_k}{\mathit{\boldsymbol{P}}_{k,{\rm{I}}}}\mathit{\boldsymbol{T}}_k^{\rm{T}}. $ | (26) |
为验证本文提出的单基线双频非组合实时精密定位方法的性能,利用4组不同基线长度的实际数据对其进行了考察.本次实验所采用的数据为2016年5月1日UNAVCO-PBO机构位于美国加利福尼亚州圣阿尔多、圣米格尔、科林加、Huasna及德拉诺的基站采集的数据,接收机采用TRIMBLE NETRS,天线类型为TRM29659.00,连续采集24 h数据,采样间隔为30 s,共2 880个历元,各组基线的具体情况如表 2所示.
| 表 2 实验数据 Table 2 The experimental data |
本次实验中的4组基线的基站接收机均位于空旷地带,可以忽略多径误差,对流层延迟误差已通过建模对原始观测量进行了补偿,因此,双差双频非组合定位模型中的主要误差为电离层延迟误差. 4组实验中,在利用扩展卡尔曼滤波器对进行状态参数估计时,状态向量中的位置参数初始值取单点定位得到的结果,对应的初始标准差设置为10 m,电离层延迟参数初始值设为0,因文中处理的最长基线为135.6 km,对应的初始标准差值统一设置为0.1 m,当基线长度更长时,需要适当调整初始标准差值,否则会影响模糊度快速固定,双差整周模糊度初始值可由双差载波相位观测值和双差伪距观测值得到,对应的标准差设为20周.文中同时利用了载波相位观测量和伪距观测量,这两种观测量的精度差别较大,因此采用随机加权模型进行调整,其中载波相位观测量对应的观测噪声标准差设为0.009 m,伪距观测量对应的观测噪声标准差设为0.9 m,两观测量内部的不同卫星-基站双差观测量采用等权模式.
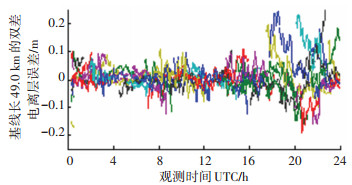
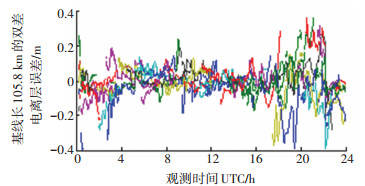
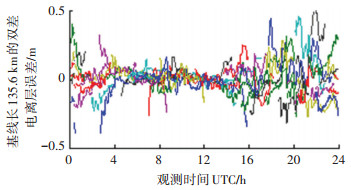
图 1~4为实验A、B、C、D根据本文所建立的实时定位模型估计出的双差电离层延迟误差,其中,图中横坐标为观测时间,纵坐标为L1载波对应的双差电离层延迟误差.

|
图 1 A组数据估计出的L1载波对应的双差电离层误差 Figure 1 Residual double difference ionospheric delay on L1 of data A |
|
图 2 B组数据估计出的L1载波对应的双差电离层误差 Figure 2 Residual double difference ionospheric delay on L1 of data B |
|
图 3 C组数据估计出的L1载波对应的双差电离层误差 Figure 3 Residual double difference ionospheric delay on L1 of data C |
|
图 4 D组数据估计出的L1载波对应的双差电离层误差 Figure 4 Residual double difference ionospheric delay on L1 of data D |
不同的颜色代表不同共视卫星对的双差电离层延迟,横坐标为观测时间,以小时为单位,对应UTC(GMT)时间0点到24点,即本地时间16点到第二天16点,图中后半段对应白天中午的电离层延迟,因此波动较大.从图中可以看出,当基线长度仅为20.7 km时,双差后的电离层延迟残差高的能达到10 cm,这对于厘米级的精密定位是不能容忍的,并且随着基线长度的增加,双差电离层延迟残差越来越大,当基线长度为135.6 km时,达到50 cm.
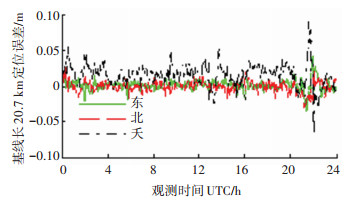
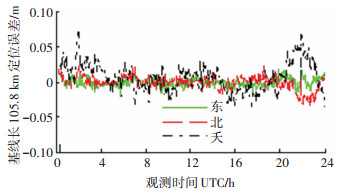
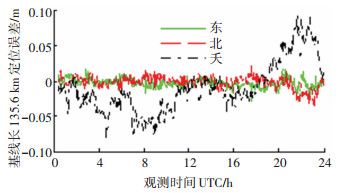
图 5~8为实验A、B、C、D的三维定位误差,其中横坐标为横坐标为观测时间,以小时为单位,对应UTC(GMT)时间0点到24点,即本地时间16点到第二天16点,纵坐标为定位误差,以米为单位,图中不同的颜色及线型分别代表东向、北向及天向误差.
|
图 5 A组数据三维定位误差 Figure 5 The positioning errors of data A |

|
图 6 B组数据三维定位误差 Figure 6 The positioning errors of data B |
|
图 7 C组数据三维定位误差 Figure 7 The positioning errors of data C |
|
图 8 D组数据三维定位误差 Figure 8 The positioning errors of data D |
表 3给出了本次实验中4组基线数据的详细定位结果.当用户与基站间的基线长度为20.7 km时,利用本文提出的实时精密定位方法,整周模糊度固定率可达98.8%,每次整周模糊度固定时间开销约为0.015 s,在利用CEP95准则统计下的东北天定位误差均为厘米级,RMS误差东向和北向达毫米级,天向为厘米级;随着用户与基站间基线长度增加,整周模糊度固定率逐渐下降,当基线长度为135.6 km时,整周模糊度固定率为97.3%,此时,CEP95准则下东北天三个方向上的误差仍为厘米级,RMS误差为厘米级.
| 表 3 整周模糊度固定率、定位结果统计比较 Table 3 Results of the experiments |
本文在单系统、单基线及双频数据条件下,提出了一种适用于中长基线的双频非组合实时精密定位方法.该方法以载波相位、伪距的站间-星间双差为基础模型,通过分析中长基线条件下主要双差残余误差量,提出相应误差处理策略,建立精密定位解算模型.为了避免引起观测矩阵秩亏,将主要误差源双差电离层延迟作为未知量,而对对流层延迟则利用Saastamoinen模型在原始观测量上进行补偿.该方法充分利用了载波相位和伪距双频观测量数据,通过随机模型调整两种观测量数据的权重,以降低低精度伪距观测量的应用带来的定位误差,最后利用扩展卡尔曼滤波器实现定位,并通过实时建立当前历元与上个历元的状态变换矩阵,保证扩展卡尔曼滤波的连续性和传递的准确性.通过4组基线实验验证了文中基于扩展卡尔曼滤波的双频非组合实时精密定位方法的有效性,基线长度达135.6 km时,该方法仍能实现厘米级的实时定位.该方法单独处理两频率上的观测量,有效避免了观测值组合过程所引起的观测噪声,是中长基线条件下单基线实时精密定位的另一种思路.
| [1] |
PAZIEWSKI J, WIELGOSZ P. Assessment of GPS+ Galileo and multi-frequency Galileo single-epoch precise positioning with network corrections[J].
GPS Solutions, 2014, 18(4): 571-579.
DOI: 10.1007/s10291-013-0355-3 |
| [2] |
KASHANI I, GREJNER D, WIELGOSZ P. Toward instantaneous network based real time kinematic GPS over 100 km distance[J].
Navigation, 2005, 52(4): 239-245.
DOI: 10.1002/j.2161-4296.2005.tb00366.x |
| [3] |
WIELGOSZ P, KASHANI I, GREJNER D. Analysis of long-range network RTK during a severe ionospheric storm[J].
Journal of Geodesy, 2005, 79(9): 524-531.
DOI: 10.1007/s00190-005-0003-y |
| [4] |
WANG D, GAO C, PAN S. Single-epoch integer ambiguity resolution for long-baseline RTK with ionosphere and troposphere estimation[C]// SUN J, JIAO W, WU H, et al. Lecture Notes in Electrical Engineering. Berlin Heidelberg: Springer, 2013: 125-137. DOI:10.1007/978-3-642-37398-5_12.
|
| [5] |
ODIJK D, TEUNISSEN P, TIBERIUS C. Triple-frequency ionosphere-free phase combinations for ambiguity resolution[C]// ASKILDT M. Proc. of the ENC-GNSS 2002. Copenhagen, Denmark: The European Navigation Conference press, 2002: 27-30.
|
| [6] |
WANG K, ROTHACHER M. Ambiguity resolution for triple-frequency geometry-free and ionosphere-free combination tested with real data[J].
Journal of Geodesy, 2013, 87(6): 539-553.
DOI: 10.1007/s00190-013-0630-7 |
| [7] |
ODIJK D. Ionosphere-free phase combinations for modernized GPS[J].
Journal of surveying engineering, 2003, 129(4): 165-173.
DOI: 10.1061/(ASCE)0733-9453(2003)129:4(165) |
| [8] |
CHAROENKALUNYUTA T, SATIRAPOD C. Effect of Thai ionospheric Maps (THIM) model on the performance of network based RTK GPS in Thailand[J].
Survey Review, 2014, 46(334): 1-6.
DOI: 10.1179/1752270613Y.0000000055 |
| [9] |
HADAS T, KAPLON J, BOSY J, et al. Near-real-time regional troposphere models for the GNSS precise point positioning technique[J].
Measurement Science and Technology, 2013, 24(5): 055003.
DOI: 10.1088/0957-0233/24/5/055003 |
| [10] |
WIELGOSZ P, KRUKOWSKA M, PAZIEWSKI J, et al. Performance of ZTD models derived in near real-time from GBAS and meteorological data in GPS fast-static positioning[J].
Measurement Science and Technology, 2013, 24(12): 125802.
DOI: 10.1088/0957-0233/24/12/125802 |
| [11] |
HU G, ABBEY D A, CASTLEDEN N, et al. An approach for instantaneous ambiguity resolution for medium-to long-range multiple reference station networks[J].
GPS Solutions, 2005, 9(1): 1-11.
DOI: 10.1007/s10291-004-0120-8 |
| [12] |
PAN S G, MENG X, WANG S L, et al. Ambiguity resolution with double troposphere parameter restriction for long range reference stations in NRTK System[J].
Survey Review, 2015, 47(345): 429-437.
DOI: 10.1179/1752270614Y.0000000144 |
| [13] |
PAZIEWSKI J. Precise GNSS single epoch positioning with multiple receiver configuration for medium-length baselines: methodology and performance analysis[J].
Measurement Science and Technology, 2015, 26(3): 035002.
DOI: 10.1088/0957-0233/26/3/035002 |
| [14] |
ODIJK D, ARORA B S, TEUNISSEN P J G. Predicting the success rate of long-baseline GPS+ Galileo (partial) ambiguity resolution[J].
Journal of Navigation, 2014, 67(3): 385-401.
DOI: 10.1017/S037346331400006X |
| [15] |
ODOLINSKI R, TEUNISSEN P J G, ODIJK D. Combined GPS+ BDS+ Galileo+ QZSS for long baseline RTK positioning[J].
Measurement Science and Technology, 2015, 26(4): 045801.
DOI: 10.1088/0957-0233/26/4/045801 |
| [16] |
PAZIEWSKI J, STEPNIAK K. New on-line system for automatic postprocessing of fast-static and kinematic GNSS data[C]// CYGAS D, TOLLAZZI T. International conference on environmental engineering (ICEE) selected papers. Vilnius, Lithuania: Vilnius Gediminas Technical University Press Technika, 2014:1-7. DOI: 10.3846/enviro.2014.235.
|
| [17] |
KHODABANDEH A, TEUNISSEN P J G. Array-based satellite phase bias sensing: theory and GPS/BeiDou/QZSS results[J].
Measurement Science and Technology, 2014, 25(9): 095801.
DOI: 10.1088/0957-0233/25/9/095801 |
| [18] |
PAZIEWSKI J, WIELGOSZ P. Accounting for Galileo-GPS inter-system biases in precise satellite positioning[J].
Journal of Geodesy, 2015, 89(1): 81-93.
DOI: 10.1007/s00190-014-0763-3 |
| [19] |
International GNSS Service. GPS satellite ephemerides / Satellite & Station Clocks[OL]. [2017-04-06]. http://www.igs.org/productsl.
|
| [20] |
WIELGOSZ P, PAZIEWSKI J, KRANKOWSKI A, et al. Results of the application of tropospheric corrections from different troposphere models for precise GPS rapid static positioning[J].
Acta Geophysica, 2012, 60(4): 1236-1257.
DOI: 10.2478/s11600-011-0078-1 |
| [21] |
BOHM J, MOLLER G, SCHINDELEGGER M, et al. Development of an improved empirical model for slant delays in the troposphere (GPT2w)[J].
GPS Solutions, 2015, 19(3): 433-441.
DOI: 10.1007/s10291-014-0403-7 |
| [22] |
LI W, YUAN Y B, OU J K, et al. A new global zenith tropospheric delay model IGG trop for GNSS applications[J].
Chinese Science Bulletin, 2012, 57(17): 2132.
DOI: 10.1007/s11434-012-5010-9 |
| [23] |
JIN S G, LUO O, REN C. Effects of physical correlations on long-distance GPS positioning and zenith tropospheric delay estimates[J].
Advances in Space Research, 2010, 46(2): 190-195.
DOI: 10.1016/j.asr.2010.01.017 |
| [24] |
SAASTAMOINEN J. Contributions to the theory of atmospheric refraction[J].
Bulletin Géodésique (1946-1975), 1973, 107(1): 13-34.
DOI: 10.1007/BF02522083 |
| [25] |
BOHM J, NIELL A, TREGONING P, et al. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data[J].
Geophysical Research Letters, 2006, 33(7): 1-4.
DOI: 10.1029/2005GL025546 |
| [26] |
唐卫明, 刘经南, 施闯, 等. 三步法确定网络RTK基准站双差模糊度[J].
武汉大学学报(信息科学版), 2007, 32(4): 305-308.
TANG W M, LIU J N, SHI C, et al. Threesteps method to determine double difference ambiguities resolution of network RTK reference station[J]. Geomatics and information science of Wuhan university, 2007, 32(4): 305-308. DOI: 10.3321/j.issn:1671-8860.2007.04.007 |
| [27] |
BETZ J W.
Engineering satellite-based navigation and timing: global navigation satellite systems, Signals, and Receivers[M]. Hoboken, New Jersey: John Wiley & Sons, 2015: 520-529.
|
| [28] |
TEUNISSEN P J G. The least-squares ambiguity decorrelation adjustment: a method for fast GPS integer ambiguity estimation[J].
Journal of geodesy, 1995, 70(1-2): 65-82.
DOI: 10.1007/BF00863419 |
| [29] |
WANG J, STEWART M P, TSAKIRI M. A discrimination test procedure for ambiguity resolution on-the-fly[J].
Journal of Geodesy, 1998, 72(11): 644-653.
DOI: 10.1007/s001900050204 |
 2017, Vol. 49
2017, Vol. 49


