非均质系统有着异于均质系统的结构动力学特性,结构的各阶振型、固有频率、阻尼等均与材料属性关系密切.目前,非均质组合系统广泛存在于船舶制造领域,主要表现为钢-复合材料的组合结构形式,国外已积极推进潜艇大型承力构件、非承力构件上的复合材料应用研究,法国“凯旋”级上60%非耐压结构都采用了结构功能一体化的声学复合材料,美国海军在声呐导流罩、透声窗、消声瓦、推进装置等局部也已实现了复合材料的实艇应用[1].
由机械振动引起的潜艇低频辐射噪声线谱,构成了潜艇的“声纹”[2],将复合材料运用在结构设计中,可以改变声辐射的特征信号.已有研究在声固耦合模型基础上,分析了机械结构板件声辐射贡献度,利用高阻尼材料进行了分布式的优化设计[3].对于阻尼性能优越复合材料,其组合结构具有显著的自噪声抑制特性.但在试验测试时,往往难以直接确定组合结构中各阶主要参与振动或噪声辐射的子系统组成.常用的模态识别方法均是通过结构测试得到有限个频响函数,并据此计算出结构总振型[4],再判别谱线峰值频率下所对应的主导振动子系统组成,然而实际结构一般较为复杂,通过试验得到完整结构的总振动、局部振动分布规律时常难以实现.
此外,对一般结构进行模态分析时,需将结构固定在基座或支撑构件上,试件与支撑构件均会不同程度的参与振动,为试件的模态振型、阻尼参数识别等带来了困难.郭雪莲[5]等对航空发动机叶片高频模态阻尼测试方法进行了描述,引入能量传递率的概念以辨识叶片的主导振动模态,为高频阻尼识别提供了解决方案.本文对组合系统振动时所表征阻尼规律进行理论分析,计算了钢-复合材料组合结构的损耗因子,将其与结构主导振动子系统的能量占比进行对比.通过试验测试验证了依据阻尼大小辨识组合结构主导振动方法的可行性.
1 非均质系统动力学及阻尼耗散机理 1.1 非均质系统的主从振动模式任何一个复杂多自由度系统均可以抽象成若干个子系统组成,一般将所关心的子系统称为主系统,其余则称为从系统,各系统间的振动是相互耦合的,主从系统的确定也是辩证的[6].对于两自由度无阻尼自由振动系统,如图 1所示,若两自由度间存在耦合,则动力学方程为
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_{11}}}&{{\mathit{\boldsymbol{M}}_{12}}}\\ {{\mathit{\boldsymbol{M}}_{21}}}&{{\mathit{\boldsymbol{M}}_{22}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\ddot x}}}_1}}\\ {{\mathit{\boldsymbol{x}}_2}} \end{array}} \right\} + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_{11}}}&{{\mathit{\boldsymbol{M}}_{12}}}\\ {{\mathit{\boldsymbol{M}}_{21}}}&{{\mathit{\boldsymbol{M}}_{22}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_1}}\\ {{\mathit{\boldsymbol{x}}_2}} \end{array}} \right\} = \left\{ \begin{array}{l} 0\\ 0 \end{array} \right\}. $ | (1) |
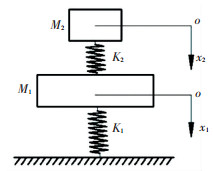
|
图 1 主从系统示意图 Figure 1 Master-slave system diagram |
该线性齐次代数方程组的非零解条件为
| $ D\left( {{\omega ^2}} \right) = \left| {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{K}}_{11}} - {\mathit{\boldsymbol{\omega }}^2}{\mathit{\boldsymbol{M}}_{11}}}&{{\mathit{\boldsymbol{K}}_{12}} - {\mathit{\boldsymbol{\omega }}^2}{\mathit{\boldsymbol{M}}_{12}}}\\ {{\mathit{\boldsymbol{K}}_{21}} - {\mathit{\boldsymbol{\omega }}^2}{\mathit{\boldsymbol{M}}_{21}}}&{{\mathit{\boldsymbol{K}}_{22}} - {\mathit{\boldsymbol{\omega }}^2}{\mathit{\boldsymbol{M}}_{22}}} \end{array}} \right| = 0. $ | (2) |
当主从系统单独存在时,固有频率为
| $ \left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\omega }}_{01}}}\\ {{\mathit{\boldsymbol{\omega }}_{02}}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {\sqrt {{\mathit{\boldsymbol{K}}_1}/{\mathit{\boldsymbol{M}}_1}} }\\ {\sqrt {{\mathit{\boldsymbol{K}}_2}/{\mathit{\boldsymbol{M}}_2}} } \end{array}} \right\}. $ | (3) |
式中: M、K分别为系统的质量、刚度矩阵,x、
| $ D\left( {{\omega ^2}} \right) = {Z^2} - \left[ {1 + \left( {1 + a} \right)\gamma } \right]Z + \gamma = 0, $ |
式中: Z=ω2/ω0i2(i=1, 2)为主从系统的无因次固有频率(平方值);a=M2/M1为从系统与主系统的质量比;γ=ω022/ω012为频率错开系数.求解得
| $ {Z_{1,2}} = \frac{{1 + \left( {1 + a} \right)\gamma \mp \sqrt {{{\left[ {1 + \left( {1 + a} \right)\gamma } \right]}^2} - 4\gamma } }}{2}. $ | (4) |
对于不同的频率错开系数γ,存在:当γ=0时,主从系统之间不发生联系,系统的两个固有频率即为二者的单独的固有频率;当γ=1时,主从系统耦合显著,且
| $ {Z_{1,2}} = \frac{{2 + a \mp \sqrt {a\left( {4 + a} \right)} }}{2}. $ | (5) |
当γ=∞时,主、从系统质量相互刚性连接.
按不同材料将系统进行主从系统分类,即使不考虑阻尼影响,子系统间的耦合影响也已不可忽视,在工程中需要从测试信号中,需要对子系统的主导振动进行辨识.
1.2 非均质系统的能量损耗特征描述根据能量耗散机理的阻尼直接描述,复刚度是包含有阻尼因素在内的刚度表达[7],为
| $ {\mathit{\boldsymbol{K}}^ * } = \mathit{\boldsymbol{K}}\left( {1 + j\eta } \right), $ | (6) |
则有阻尼的多自由度系统,存在
| $ \left[ \mathit{\boldsymbol{M}} \right]\left\{ {\mathit{\boldsymbol{\ddot x}}} \right\} + \left[ {\mathit{\boldsymbol{K}}\left( {1 + j\eta } \right)} \right]\left\{ \mathit{\boldsymbol{x}} \right\} = \left\{ \mathit{\boldsymbol{F}} \right\}. $ | (7) |
式中: η为损耗因子,表示位移对力或应变对应力的滞后;F为载荷向量.对于由多个子系统组成的系统,其中第i个子系统若有耗能,则损耗因子为
| $ {\eta _i} = \Delta {U_i}/{U_i}. $ | (8) |
n个子系统中有m个子系统在振动中损耗能量,则系统的总损耗因子为
| $ \eta = \frac{{\Delta {U_{{\rm{total}}}}}}{{{U_{{\rm{total}}}}}} = \frac{{\sum\limits_{j = 1}^m {\Delta {U_j}} }}{{\sum\limits_{i = 1}^n {{U_i}} }} = \frac{{\sum\limits_{j = 1}^m {{\eta _j}{U_j}} }}{{\sum\limits_{i = 1}^n {{U_i}} }}. $ | (9) |
式中ΔUi、Ui分别为第i个子系统损耗、储存能量.
1.3 各子系统能量耗散成分分析统计能量分析中将系统总损耗因子分为子系统的内损耗因子和子系统间的耦合损耗因子两部分[8],即并不是各子系统损耗因子的线性组合,但系统总体损耗能量是各子系统能耗的线性叠加,如式(9).
形成阻尼的机理有很多,在实际问题分析时很难将所有机理都考虑在内.一般情况下,结构第i个子系统的内损耗因子ηi主要由结构损耗因子ηis、声辐射损耗因子ηir和边界损耗因子ηib三类独立成分组成,分别对应于系统本身的材料阻尼、流体介质阻尼和系统边界连接阻尼.可表示为
| $ {\eta _i} = {\eta _{i{\rm{s}}}} + {\eta _{i{\rm{r}}}} + {\eta _{i{\rm{b}}}}. $ | (10) |
对于均质材料结构,假设在刚性一体化连接下无边界损耗,且不计声辐射损耗时,将结构细分为无限个子系统后,令β为材料损耗因子,第i个子系统内损耗因子存在关系
| $ {\eta _i} = {\eta _{is}} = {\beta _i}. $ | (11) |
按式(9)可得到系统第q阶模态内损耗因子为
| $ {\eta ^{\left( q \right)}} = \frac{{\sum\limits_{j = 1}^m {{\eta _j}U_j^{\left( q \right)}} }}{{\sum\limits_{i = 1}^n {U_i^{\left( q \right)}} }} = \frac{{\sum\limits_{j = 1}^m {{\beta _j}U_j^{\left( q \right)}} }}{{\sum\limits_{i = 1}^n {U_i^{\left( q \right)}} }}\xrightarrow[{m = n}]{{{\beta _j} = \beta }}\beta \frac{{\sum\limits_{j = 1}^m {U_j^{\left( q \right)}} }}{{\sum\limits_{i = 1}^n {U_i^{\left( q \right)}} }} = \beta . $ | (12) |
可见,对于真空状态下均质材料组成的刚性连接结构,其系统内损耗因子与材料损耗因子相等;
对于非均质的组合结构,即使不计边界损耗与声辐射损耗,系统第q阶模态内损耗因子为
| $ {\eta ^{\left( q \right)}} = \frac{{\sum\limits_{j = 1}^m {{\eta _j}U_j^{\left( q \right)}} }}{{\sum\limits_{i = 1}^n {U_i^{\left( q \right)}} }} = \frac{{\sum\limits_{j = 1}^m {{\beta _j}U_j^{\left( q \right)}} }}{{\sum\limits_{i = 1}^n {U_i^{\left( q \right)}} }}\xrightarrow[{m = n}]{{{\beta _j}\;互不相等}}\frac{{\sum\limits_{j = 1}^m {{\beta _j}U_j^{\left( q \right)}} }}{{\sum\limits_{i = 1}^n {U_i^{\left( q \right)}} }}. $ | (13) |
可见,非均质系统的内损耗因子还与子系统的材料构成、结构形式等相关,在全频段上不仅受材料的频变特性影响,还随振型而变化(即参与耗能的子系统组合不同).
2 非均质组合系统损耗特征数值分析 2.1 测试结构及有限元模型描述对玻璃钢、结构钢壳板与钢工装的组合结构进行测试,相关参数见表 1.工装为钢材,其内腔体尺寸为600 mm×600 mm×500 mm,结构见图 2.针对上述测试系统建立有限元模型,壳板单元采用实体单元建模,计算时考虑纤维铺层方向、角度和厚度等,工装采用壳单元建模,工装底部刚性固支.
| 表 1 壳板结构及材料性能参数 Table 1 Shell structure and material performance parameters |

|
1—上盖板; 2—壳板模型; 3—加强筋; 4—底座 图 2 工装模型 Figure 2 Tooling model |
为获得精确的材料损耗因子参数,首先利用DMA粘弹仪对玻璃钢、结构钢的试件进行材料损耗因子测试,得到指定温-频下的材料损耗因子曲线(10 ℃下50~1 000 Hz频段),如图 3.纤维增强材料与普通粘弹性材料不同,其玻璃化温度较高,频域内损耗因子极大值出现在极低频率处,且在50~1 000 Hz频段内损耗因子βf呈现随频率增大而略有减小的规律,处于0.007~0.008 5之间;钢材的损耗因子βs很低,处于0.000 1附近,约为玻纤增强树脂的1/80左右.对二者数据进行拟合,取该频段内的βf≈ 0.008、βs≈0.000 1,以简化下节理论分析计算.

|
图 3 壳板的材料损耗因子曲线 Figure 3 Material loss factor curves of shell plate |
已有文献[9]给出,复特征值法通过有阻尼结构的正交模态来求解,所得特征值和特征向量均为复数,且特征向量是正交的,可解耦动力方程.建立有阻尼结构的有限元模型并引入材料阻尼,利用MSC.Nastran中的SOL 107模块得到阻尼结构的固有频率和模态结构损耗因子[3].
复特征值的定义为:
| $ p = \alpha + i\omega . $ | (14) |
式中: α是阻尼结构衰减率的度量,ω是结构的圆频率.所得结构损耗因子ηs=-2α/|ω|.该系统结构损耗因子考虑了子系统的材料特性、构成形式等因素以及子系统间耦合效果,利于总体损耗的描述.
进行子系统能量占比理论分析时,未将子系统与流体介质耦合作用下的声辐射损耗因子ηir和边界非刚性一体化连接影响下的边界损耗因子ηib考虑在内,利用复特征值法计算得到组合系统的模态结构损耗因子ηis,探究了各子系统对该损耗因子的贡献规律.
将所测试系统按照板单元、工装分为两个子系统,即子系统1、2.仿真建模时将壳板与工装间的节点刚性连接,总损耗因子为:
| $ \eta = \frac{{{\eta _1}{U_1} + {\eta _2}{U_2}}}{{{U_1} + {U_2}}}. $ | (15) |
式中: U1、U2分别为子系统1、2的储存能量;η1、η2分别为子系统1、2独立存在时的损耗因子,由式(11)、(12)可知,存在η1=βf、η2=βs;η可由复特征值法计算得到.则:
| $ \frac{{{U_1}}}{{{U_2}}} = \frac{{\eta - {\eta _1}}}{{{\eta _2} - \eta }}. $ | (16) |
测试时主要关心壳板的振动,然而经模态计算发现,对于由玻璃钢-工装组合的结构系统,仅对玻璃钢板模态提取分析时,相似壳板振型却存在多个阶次的模态固有频率,如表 2所示. 表 2中第一行给出了固支方形壳板的理论振动模态振型(前6阶),第二、三行分别给出了对应第一行的理论振型下,壳板、工装主导参与振动的系统总振动模态及阶次.
| 表 2 玻璃钢壳板-工装组合系统壳板相似振型对比图 Table 2 Fiber glass shell plate-tooling combination system vibration pattern diagram |
对于仿真计算,可以从系统总体模态振型图中直接获得所关心的(壳板主导)振动模态阶次,而在试验测试时,往往仅会在壳板上布置测点,所得振型图也只能反映组合系统中壳板振动那一部分.若不针对上述情况进一步分析,则无法从多个模态结果中识别壳板主导振动的阶次,因此需要剔除由工装大量参与振动下的模态阶次.
本文根据复特征值法数值计算得到结构钢、玻璃钢壳板与工装组合下各阶固有频率、模态损耗因子,结合式(16)理论分析得到玻璃钢壳板-工装系统的各阶振动能量中子系统能量占比,对比结果如表 3和图 4~5所示.
| 表 3 系统模态参数及子系统能量占比结果 Table 3 System modal parameters and subsystem energy accounting results |
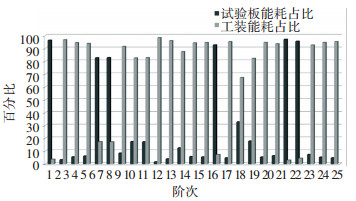
|
图 4 各阶模态下的子系统能量占比(玻璃钢壳板) Figure 4 The energy ratio ofsubsystems in each mode (fiber glass) |
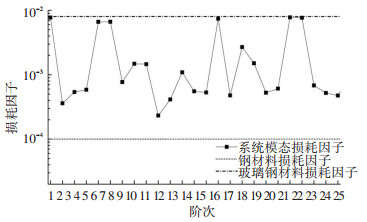
|
图 5 系统各阶模态损耗因子(玻璃钢壳板) Figure 5 Modular loss factor of the system (fiber glass) |
由表 3可见,在不计系统的边界损耗和声辐射损耗的情况下,由钢板-工装所构成的模型,其模态损耗因子与钢的材料损耗因子相同,不受振型和结构形式的影响;由玻璃钢板-工装所构成的钢-复合材料组合结构,其模态损耗因子随振型、频率而变,主要由于参与振动的子系统耗能占比不同,各子系统能量损耗能力存在差异.
进一步结合表 3中数据对图 4~5进行分析. 图 4可见,玻璃钢壳板子系统在组合系统模态的第1、5、6、15、21、22阶中振动能量占比较大,在振动中起主导作用,而与上述壳板振型相似的第2、3、4、12、7、11阶组合系统振动模态中,工装参与振动的能量占比却很大.据此,与图 5作对比分析可见,当壳板主导振动时,组合系统模态内损耗因子接近于玻璃钢的材料损耗因子βf;而当工装主导振动时,组合系统模态内损耗因子接近于钢的材料损耗因子βs.
在不计边界和声辐射损耗时,均质系统的各阶模态内损耗因子η(q)与材料损耗因子相同;非均质系统的各阶模态内损耗因子η(q)则同时由材料损耗和振型所决定,且组合系统的η(q)数值上接近于主导振动子系统的材料损耗因子,介于各子系统材料损耗因子的极(大/小)值之间.根据这一原则可实现对复杂非均质系统中主导振动子系统的识别.
3 主导振动子结构的测试识别 3.1 测试环境及方法对图 2所示的实际结构进行测试,用盖板与螺钉将壳板与工装紧固约束连接,模态参数识别采用多点激励多点拾振法(以辨别结构的模态重根),激励形式为力锤作用下的脉冲激励,板正面均布121个激励点,背面均布9个加速度响应拾振点.激振点、拾振点布置见图 6.
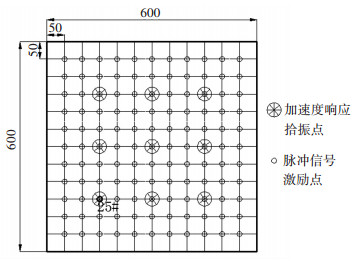
|
图 6 壳板测点布置 Figure 6 Shell plate measuring point layout |
利用DHDAS信号采集仪中的Polylscf法对结构进行分析,该方法是国际最新发展并流行的基于传递函数的模态分析方法,可在模态较密集的系统、FRF数据受到严重噪声污染的情况下仍建立清晰的稳态图,较高精度地识别出模态固有频率、阻尼和振型.
3.2 响应频谱及模态识别结果分析以玻璃钢壳板数值计算及试验测试结果为例,相似板单元振型确实对应存在多个固有频率和阻尼参数组合,即相似局部壳板振动形式下,存在多个阶次的系统总振动模态,需要对该系统下的壳板主导振动模态进行判断.
根据图 6所示的测点编号,取25#点激励下,9个响应拾振点的频响函数包络线进行分析,以将各谱线峰值集中在一条曲线中,如图 7所示(其中数字标出了要进行判别的峰值,带星号的是玻璃钢板主导振动的峰值).
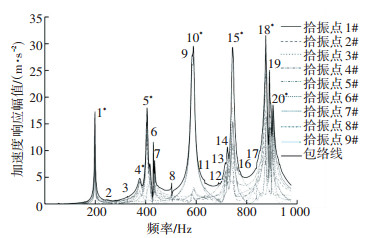
|
图 7 系统频响函数包络线(玻璃钢板) Figure 7 System frequency response envelope (fiber glass) |
图 7中的谱线峰值进行模态识别和阻尼比计算,壳板主导振动辨识结果见表 4所示.其中,第1阶与第2阶、第3阶与第4阶、第9阶与第10阶等均各自具有相似的板单元振型(见表 2分析),但第2、3、9阶与第6、7、8、11等阶次模态参数类似,其模态阻尼比均较小,谱峰能量较小,判断该响应峰值为工装主导参与振动情况下的板单元局部振动,反之,第1、4、5、10、14、15、18、20阶均为玻璃钢壳板主导振动.
| 表 4 玻璃钢壳板主导振动模态内损耗因子 Table 4 The loss factor of the dominant vibration mode of fiber glass shell plate |
经测试发现,该组合系统的模态内损耗因子ηi测试结果较模态结构损耗因子ηis增大许多,主要在于实际模型中试验板与工装采用了螺钉连接,两个子系统间存在边界损耗ηib,同时空气中的振动还存在声辐射损耗ηir.张永杰[10]等对钢板在空气中的声辐射损耗因子进了分析,本文结合该研究,利用统计能量法对玻璃钢壳板的系统模型完成了声辐射损耗因子ηir计算,并基于DMA材料损耗因子实测曲线数据,计算该组合系统结构损耗因子ηis,得到以玻璃钢壳板主导振动的前8阶损耗因子见表 4,以及系统在50~1 000 Hz频段下的损耗因子组成如图 8所示.

|
图 8 玻璃钢壳板主导振动下模态内损耗因子组成对比 Figure 8 Comparison of loss factor composition in the dominant vibration mode of glass fiber shell plate |
图 8可知,玻璃钢板的系统内损耗因子ηi主要由ηis和ηib所组成,且二者占比相当;试验中空气声辐射损耗因子ηir与ηi相差1~2个数量级,对ηi的贡献几乎可以忽略;此外测试所得ηib在研究频段内较为接近,均在0.006~0.008区间内,在进行研究时,实际结构的边界损耗不容忽视.
4 结论根据工程运用的实际需求,本文分析了常见钢-复合材料组合结构的振动模式,利用主从振动等理论对非均质组合系统振动特性及其能量耗散规律进行了描述,结合统计能量原理中关于系统损耗因子的分类,经计算指出,在不计边界损耗与声辐射损耗情况下:
1) 均质材料的组合结构,其系统内损耗因子与材料损耗因子相等;
2) 非均质材料的组合结构,系统内损耗因子还与子系统的组成相关,且在频域上受材料的频变特性和振型影响.
进一步对组合系统振动中的子系统振动能量占比,及其损耗组成规律进行分析.认为在排除声辐射损耗和边界损耗影响后,非均质组合系统的内损耗因子ηi数值上接近于其主导振动子系统的材料损耗因子,介于各子系统材料损耗因子的极(大/小)值之间.由于复合材料的材料损耗因子较钢材至少高出几十倍,一般易于从损耗因子的量值上判断出主导振动的子系统.
这种运用阻尼量值来辨识非均质系统中主导振动子系统的方法简单快速,为复杂系统的模态识别提供了技术支持.
| [1] |
陈锋, 齐国英, 赖鸣, 等. 国外新型核潜艇技术特征研究[J].
舰船科学技术, 2014, 36(9): 153-157.
CHEN Feng, QI Guoying, LAI Ming, et al. Research on technical characteristic of foreign new generation nuclear submarine[J]. Ship Science and Technology, 2014, 36(9): 153-157. |
| [2] |
夏齐强, 陈志坚. 降低加肋双层圆柱壳辐射噪声线谱的结构声学设计[J].
声学学报, 2014, 39(5): 613-622.
XIA Qiqiang, CHEN Zhijian. Structural-acoustic design to depress line spectrum of radiation noise from double cylindrical ring stiffened shell[J]. ACTA ACUSTICA, 2014, 39(5): 613-622. |
| [3] |
张俊红, 李忠鹏, 毕凤容, 等. 基于板件贡献分析的装载机驾驶室低噪声设计[J].
振动、测试与诊断, 2016, 36(3): 568-574.
ZHANG Junhong, LI Zhongpeng, BI Fengrong, et al. Low noise optimization design of loader cab based on panel contribution analysis[J]. Journal of Vibration, Measurement and Diagnosis, 2016, 36(3): 568-574. |
| [4] |
李德葆, 陆秋海.
实验模态分析及其应用[M]. 北京: 科学出版社, 2001: 58-67.
|
| [5] |
郭雪莲, 范雨, 李琳. 航空发动机叶片高频模态阻尼的实验测试方法[J].
航空动力学报, 2014, 29(9): 2104-2112.
GUO Xuelian, FAN Yu, LI Lin. Experimental test method for high-frequency modal damping of turbo machinery blades[J]. Journal of Aerospace Power, 2014, 29(9): 2104-2112. |
| [6] |
金咸定.
船体振动学[M]. 上海: 上海交通大学出版社, 1987: 122-125.
|
| [7] |
戴德沛.
阻尼减振降噪技术[M]. 西安: 西安交通大学出版社, 1986: 38-40.
|
| [8] |
姚德源, 王其政.
统计能量分析原理及其应用[M]. 北京: 北京理工大学出版社, 1995: 68-79.
|
| [9] |
邹经湘, 李强. 在非比例阻尼情况下识别模态参数[J].
哈尔滨工业大学学报, 1985, special: 91-98.
ZOU Jingxiang, LI Qiang. Identifying modal parameters in case of non-proportional damping[J]. Journal of Harbin Institute of Technology, 1985, special: 91-98. |
| [10] |
张永杰, 肖健, 韦冰峰, 等. 一种新的基于脉冲激励的内损耗因子获取方法[J].
振动与冲击, 2014, 32(12): 161-164.
ZHANG Yongjie, XIAO Jian, WEI Bingfeng, et al. A new method for estimating damping loss factor based on multi-pulse excitation[J]. Journal of Vibration and Shock, 2014, 32(12): 161-164. |
 2017, Vol. 49
2017, Vol. 49