多轴循环应力-应变关系是指材料在多轴载荷下应力-应变响应的变化关系.目前主要有两种方法来描述这种变化关系[1]:一种是经验公式法,另一种是循环本构模型.经验公式法是基于全量理论来描述多轴循环应力-应变关系.这种方法简单、实用、方便.但是,经验公式法仅仅能较好地描述几种典型多轴加载下的应力-应变关系.因此,各国研究者更多的是基于增量理论,利用循环本构模型来描述材料的应力-应变关系.
20世纪60年代以来,人们提出了众多基于增量理论的循环本构模型,但不论何种模型,大都由三个基本部分组成[2]:屈服准则;流动规律;硬化规律.对于屈服准则和流动规律,各模型基本都相同.而硬化规律随着加载方式的逐渐复杂,被不断修正,从最初的线性硬化规律逐渐发展到非线性硬化规律. Armstrong等[3](A-F模型)在随动强化律的基础上,通过引入一个动态恢复项使随动强化率具有非线性特征,建立了著名的动力恢复模型. Chaboche等[4]提出非线性硬化规律可以用一系列的背应力分量来表示,对A-F模型进行修正.杨显杰等[5]定义材料的屈服面和极限面分别遵循不同的演化规律,通过引入加载路径的非比例度,提出一个可考虑材料循环强化/软化效应、塑性应变历史效应和非比例循环加载效应的双曲面模型. Döring等[6]分析发现Jiang模型[7]不能很好的反映材料的非比例附加强化现象,通过引入Tanaka非比例度因子[8],对Jiang模型进行修正. Khutia等[9]也通过引入Tanaka非比例度因子[8]对Chen等修正的Ohno-Wang模型[10]进行了进一步修正,并利用304不锈钢的试验结果对修正模型进行验证. Meggiolaro等[11]对Tanaka非比例度因子进行瞬态响应修正,并引入到Jiang模型中,较好地描述了316L不锈钢的非比例附加强化现象. Gates等[12]基于Tanaka非比例度因子提出一个新的瞬态硬化准则,并利用该准则对Zhang-Jinag模型[13]进行修正,修正模型较好地描述多种复杂载荷路径下2024-T3铝合金的非比例附加强化现象. Wu等[14]利用Tanaka非比例度因子[8],在退化的2维偏应力-应变空间中量化了塑性应变对广义塑性模量的影响,所建多轴本构关系可以体现三种强化效应. Shamsaei等[15]利用304L不锈钢和1050QT合金钢系统研究了多种复杂非比例加载路径下材料的附加强化效应,通过验证发现Tanaka非比例度因子[10]可较好地反映材料的非比例附加强化现象.虽然Tanaka非比例度因子应用较为广泛,但是该因子中的材料常数需要借助相关多轴疲劳试验予以确定[16].
Itoh等[17]引入一个新的非比例度因子,建立一个新的循环本构模型,该模型可以描述材料的非比例附加强化现象,且只含有6个材料常数,便于计算.但是,利用多种复杂多轴加载下6061-T6铝合金的试验结果对模型进行验证发现,模型中的附加强化系数对模型的计算精度影响较大,而合理地确定附加强化系数,就需要借助材料的多轴疲劳试验数据,给模型的进一步应用带来不便. Kowalewski等[18]建立一个三曲面本构模型,并利用新模型较好地描述了2024铝合金的单/多轴应力-应变响应.但是,该模型的材料常数较多且大多需要借助试验予以确定,而Kowalewski等[18]未给出这些材料常数的具体确定方法. Madrigal等[19]通过定义应力空间相邻加载点的距离方程,建立一个新的多轴本构模型.但是,该距离方程也需要借助多轴疲劳试验予以确定.概括来讲,对于建立在A-F模型[3]基础上,塑性模量通过一致性条件得到的耦合类本构模型,至少存在以下三方面的问题:模型中材料参数较多,计算繁琐;需要较多的附加单轴及多轴疲劳试验来确定模型中的材料常数;模型过于复杂,不利于工程应用.
为克服现有本构模型的上述缺点,本文在A-F模型背应力演化方程的基础上,通过引入非比例度因子和附加强化系数,构建一个新的背应力演化方程.然后,通过一致性条件建立塑性模量方程与背应力之间的关系.同时,利用最小法向应变范围,提出一种计算非比例度因子的新方法.利用多种多轴加载路径下S460N钢和304L不锈钢的试验结果对模型进行了验证,预测结果与试验结果吻合良好.
1 多轴循环本构模型的描述一个完整的循环塑性本构模型一般由屈服准则、流动规律和硬化规律三部分组成.在弹性范围内,应力可利用Hooke定律由应变确定,但在循环塑性变形过程中,应力-应变取决于加载历史,应力-应变通常利用增量理论来确定.
1.1 屈服准则对于复杂应力状态,材料是否进入塑性状态,一方面和这些应力分量有关,另一方面与材料的力学性能有关.就大多数金属材料而言,恒温下受到循环加载时,应当主要考虑加载历史对应力-应变响应的影响.本文定义屈服条件服从von-Mises屈服准则
| $ {F_i}\left( {\mathit{\boldsymbol{s}},\mathit{\boldsymbol{\alpha }},k} \right) = \left( {\mathit{\boldsymbol{s}} - \mathit{\boldsymbol{\alpha }}} \right):\left( {\mathit{\boldsymbol{s}} - \mathit{\boldsymbol{\alpha }}} \right) - 2{k^2}. $ | (1) |
式中: s为偏应力张量,α为背应力张量,k为单剪状态下的屈服强度,张量之间的“:”表示张量的点积.
1.2 流动规律根据小变形理论,总应变增量dεt由弹性应变增量dεe和塑性应变增量dεp两部分组成
| $ {\rm{d}}{\mathit{\boldsymbol{\varepsilon }}_{\rm{t}}} = {\rm{d}}{\mathit{\boldsymbol{\varepsilon }}_{\rm{e}}} + {\rm{d}}{\mathit{\boldsymbol{\varepsilon }}_{\rm{p}}}. $ | (2) |
式中弹性应变增量dεe可由Hooke定律求得
| $ {\rm{d}}{\mathit{\boldsymbol{\varepsilon }}_{\rm{e}}} = \frac{{1 + {\nu _e}}}{E}\left[ {{\rm{d}}\sigma - \frac{{{\nu _e}}}{{1 + {\nu _e}}}\left( {{\rm{d}}\mathit{\boldsymbol{\sigma }}:\mathit{\boldsymbol{I}}} \right)\mathit{\boldsymbol{I}}} \right]. $ | (3) |
式中:E为弹性模量,νe为弹性泊松比,dσ为应力增量张量,I为二阶单位张量.塑性应变增量dεp可由流动规律求得[2, 7]:
| $ {\rm{d}}{\varepsilon _{\rm{p}}} = \frac{1}{H}\left\langle {{\rm{d}}\mathit{\boldsymbol{s}}:\mathit{\boldsymbol{n}}} \right\rangle \mathit{\boldsymbol{n}}, $ | (4) |
其中:
| $ H = \frac{{\mathit{\boldsymbol{n}}:{\rm{d}}\mathit{\boldsymbol{\alpha }}}}{{{\rm{d}}p}}, $ | (5) |
| $ {\rm{d}}p = \sqrt {{\rm{d}}{\mathit{\boldsymbol{\varepsilon }}_{\rm{p}}}:{\rm{d}}{\mathit{\boldsymbol{\varepsilon }}_{\rm{p}}}} , $ | (6) |
| $ \mathit{\boldsymbol{n}} = \frac{{\mathit{\boldsymbol{s}} - \mathit{\boldsymbol{\alpha }}}}{{\left\| {\mathit{\boldsymbol{s}} - \mathit{\boldsymbol{\alpha }}} \right\|}}, $ | (7) |
| $ {\rm{d}}\mathit{\boldsymbol{s}} = 2G{\rm{d}}\mathit{\boldsymbol{e}} = 2G\left[ {{\rm{d}}{\varepsilon _{\rm{t}}} - {\rm{d}}{\varepsilon _{\rm{p}}} - \frac{1}{3}\left( {{\rm{d}}{\varepsilon _{\rm{t}}}:\mathit{\boldsymbol{I}}} \right)\mathit{\boldsymbol{I}}} \right]. $ | (8) |
式中:“〈〉”为MacCauley括号,“‖‖”为张量函数的模,de为偏弹性应变增量,G为剪切模量.
由式(4)可知,当ds:n>0时,材料产生塑性变形.由式(4)~(8),可得
| $ {\rm{d}}{\mathit{\boldsymbol{\varepsilon }}_{\rm{p}}} = \frac{{2G}}{{2G + H}}\left( {{\rm{d}}{\mathit{\boldsymbol{\varepsilon }}_{\rm{t}}}:\mathit{\boldsymbol{n}}} \right)\mathit{\boldsymbol{n}}. $ | (9) |
对于控制应力加载,塑性应变增量可用式(4)进行计算.对于控制应变加载,与式(4)相比,塑性应变增量利用式(9)进行计算更为方便.
1.3 硬化规律Jiang等[20]将A-F模型中的背应力演化方程重新表述为
| $ {\rm{d}}{\mathit{\boldsymbol{\alpha}}} = cr\left( {\mathit{\boldsymbol{n}} - \frac{\mathit{\boldsymbol{\alpha }}}{r}} \right){\rm{d}}p. $ | (10) |
式中c和r都是材料常数.
在A-F模型中,材料常数c和r的确定方法繁琐,而且在非比例加载下,利用单轴疲劳试验数据确定的材料常数并不能很好地反映材料的附加强化现象.为此,本文引入附加强化系数和非比例度因子对A-F模型的背应力演化方程进行进一步修正.
Socie等[2]指出,多轴加载下,材料的应力-应变关系可用Ramberg-Osgood公式为
| $ {\sigma _{{\rm{eq}}}} = \left( {1 + {\alpha _{{\rm{np}}}}{f_{{\rm{np}}}}} \right)K'{\left( {{\varepsilon _{{\rm{eq,p}}}}} \right)^{n'}}. $ | (11) |
此时,材料的塑性模量为
| $ H = {\left( {1 + {\alpha _{{\rm{np}}}}{f_{{\rm{np}}}}} \right)^{\frac{1}{{n'}}}}{{K'}^{\frac{1}{{n'}}}}n'\sigma _{{\rm{eq}}}^{\frac{{n' - 1}}{{n'}}}. $ | (12) |
式中:σeq为von-Mises等效应力,εeq, p为von-Mises等效塑性应变,K′为循环强度系数,n′为循环应变硬化指数,fnp为非比例度因子.附加强化系数αnp定义为[1]
| $ {\alpha _{np}} = \frac{{\sigma _{{\rm{OP}}}^a}}{{\sigma _{{\rm{IP}}}^a}} - 1. $ | (13) |
式中: σOPa为非比例圆路径加载(fnp=1)下的等效应力幅值;σIPa为相同等效应变时,比例加载路径(fnp=0)下的等效应力幅值.
将式(10)代入式(5),可得
| $ H = cr\left( {1 - \frac{{\mathit{\boldsymbol{\alpha }}:\mathit{\boldsymbol{n}}}}{r}} \right). $ | (14) |
由式(14)中求出cr后代入式(10),可得
| $ {\rm{d}}\alpha = \frac{H}{{1 - \frac{{\mathit{\boldsymbol{\alpha }}:\mathit{\boldsymbol{n}}}}{r}}}\left( {\mathit{\boldsymbol{n}} - \frac{\mathit{\boldsymbol{\alpha }}}{r}} \right){\rm{d}}p. $ | (15) |
将式(12)代入式(15),可得背应力演化方程为
| $ {\rm{d}}\mathit{\boldsymbol{\alpha }} = \frac{{{{\left( {1 + {\alpha _{np}}{f_{np}}} \right)}^{\frac{1}{{n'}}}}{{K'}^{\frac{1}{{n'}}}}n'\sigma _{{\rm{eq}}}^{\frac{{n' - 1}}{{n'}}}}}{{1 - \frac{{\mathit{\boldsymbol{\alpha }}:\mathit{\boldsymbol{n}}}}{r}}}\left( {\mathit{\boldsymbol{n}} - \frac{\mathit{\boldsymbol{\alpha }}}{r}} \right){\rm{d}}p. $ | (16) |
试验验证发现,当r取值远大于材料的屈服面半径时,r取值对材料应力-应变响应的计算结果影响不大.因此,本文中将材料常数r取为K′.
根据一致性条件可知,单轴循环加载下,式(16)确定的塑性模量方程退化为由Ramberg-Osgood曲线确定的单轴塑性模量方程.
1.4 非比例度因子用K′代替式(16)中的材料常数r后,除了K′和n′,式(16)中不含有额外的材料常数.但是,在计算过程中,需要确定不同加载路径下的非比例度因子fnp,以反映加载路径非比例程度对材料循环应力-应变的影响.因此,进一步建立fnp的计算公式.
拉扭加载下,与薄壁圆管试件轴向夹角为α的平面上的法向应变εn, α和剪切应变γα分别为[21]:
| $ {\varepsilon _{n,\alpha }} = \frac{{1 - {\nu _{{\rm{eff}}}}}}{2}{\varepsilon _x} + \frac{{1 - {\nu _{{\rm{eff}}}}}}{2}{\varepsilon _x}\cos 2\alpha + \frac{1}{2}{\gamma _{xy}}\sin 2\alpha , $ | (17) |
| $ {\gamma _\alpha } = - \left( {1 + {\nu _{{\rm{eff}}}}} \right){\varepsilon _x}\sin 2\alpha + {\gamma _{xy}}\cos 2\alpha . $ | (18) |
式中νeff为等效泊松比,可将其取为0.5[2].
以正弦波加载为例,在控制应变下对薄壁圆管试件施加的轴向应变εx和剪切应变γxy为:
| $ {\varepsilon _x} = \frac{{\Delta {\varepsilon _{{\rm{app}}}}}}{2}\sin \omega t, $ | (19) |
| $ {\gamma _{xy}} = \frac{{\Delta {\gamma _{{\rm{app}}}}}}{2}\sin \left( {\omega t - \varphi } \right). $ | (20) |
式中: Δεapp和Δγapp分别为施加的轴向和剪切应变范围,φ为载荷间的相位差.
由式(17)~(20)可得,与薄壁圆管试件轴向夹角为α的平面上的法向应变范围Δεn, α和剪切应变范围Δγα分别为[21]:
| $ \begin{array}{l} \Delta {\varepsilon _{n,\alpha }} = \frac{1}{2}\Delta {\varepsilon _{{\rm{app}}}}\left\{ {{{\left[ {\lambda \sin 2\alpha \sin \varphi } \right]}^2} + \left[ {2\left( {1 + } \right.} \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\;{\left. {{{\left. {\left. {{\nu _{{\rm{eff}}}}} \right){{\cos }^2}\alpha - 2{\nu _{{\rm{eff}}}} + \lambda \sin 2\alpha \cos \varphi } \right]}^2}} \right\}^{0.5}}, \end{array} $ | (21) |
| $ \begin{array}{l} \Delta {\gamma _\alpha } = \Delta {\varepsilon _{{\rm{app}}}}\left\{ {{{\left[ {\lambda \cos 2\alpha \sin \varphi } \right]}^2} + \left[ {\lambda \cos 2\alpha \cos \varphi - } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;{\left. {{{\left. {\left( {1 + {\nu _{{\rm{eff}}}}} \right)\sin 2\alpha } \right]}^2}} \right\}^{0.5}}. \end{array} $ | (22) |
式中λ(=Δγapp/Δεapp)为应变比.
利用式(21),图 1为等效应变范围为1.2%、应变比为
| $ {f_{{\rm{np}}}} = \frac{{{{\left( {\Delta {\varepsilon _{n,\alpha }}} \right)}_{\min }}}}{{\max \left( {{{\left( {\Delta {\varepsilon _{n,\alpha }}} \right)}_{\min }}} \right)}}. $ | (23) |

|
图 1 不同相位差下各平面的法向应变范围(正弦波) Figure 1 The normal strain range, Δεn, α, of each plane under different phase delays (sinusoidal wave) |
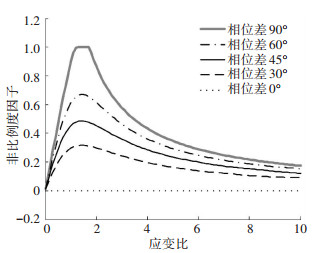
图 2所示为正弦波加载下,不同相位差时的非比例度因子fnp与应变比λ之间的关系.由图可见,比例加载下,由式(23)计算得到的非比例度因子恒等于零;非比例加载下,fnp随应变比λ的增加,先增大后减小,当应变比λ趋近于零(单轴加载)或无穷大(纯扭转加载)时,fnp趋近于零.与之相比,相位差无法描述相位差相同,应变比不同时加载路径的非比例程度.因此,本文定义的非比例度因子克服利用相位差描述加载路径非比例程度的这一不足.另外,由图 2还可发现,最大非比例度因子fnp并非出现在某一应变比下,而是出现在应变比λ=1.5附近的一个区间段内.当相位差为90°时,Ellyin等[22]通过试验发现应变比λ=1时加载路径的非比例程度最大.而Kanazawa等[23]和Benallal等[24]发现应变比λ分别为1.5和
|
图 2 非比例度因子fnp随应变比λ的变化 Figure 2 Correlation between the nonproportionality factor, fnp, and the strain ratio, λ |
当加载波形为正弦波且轴向应变εx和剪切应变γxy的加载频率相同时,可直接利用式(21)和式(23)来计算加载路径的fnp.对于一般的多轴加载情形,利用式(23)计算fnp的具体步骤如下:
1) 根据输入的轴向应变εx和剪切应变γxy,确定加载路径形状;
2) 对于一个加载周期,以微小的时间步长Δt,将εx和γxy进行离散;
3) 计算不同时刻,第i个平面(αi)上的法向应变:
| $ \begin{array}{l} {\varepsilon _{n,{\alpha _i}}}\left( j \right) = \left( {\frac{{1 - {\nu _{{\rm{eff}}}}}}{2} + \frac{{1 + {\nu _{{\rm{eff}}}}}}{2}\cos 2{\alpha _i}} \right){\varepsilon _x}\left( {j\Delta t} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}{\gamma _{xy}}\left( {j\Delta t} \right)\sin 2{\alpha _i}\;\;\;\;j = 1,2, \cdots ,q. \end{array} $ | (24) |
式中q表示一个循环内离散的载荷步数.
4) 计算第i个平面(αi)上的法向应变范围:
| $ \Delta {\varepsilon _{n,{\alpha _i}}} = \max \left( {{\varepsilon _{n,{\alpha _i}}}\left( j \right)} \right) - \min \left( {{\varepsilon _{n,{\alpha _i}}}\left( j \right)} \right). $ | (25) |
5) 让i在[0°, 180°)内以1°为步长变化,计算各平面上的法向应变范围.比较各平面上法向应变范围的大小,确定最小法向应变范围(Δεn, α)min的值;
6) 利用式(21)计算相同等效应变时,圆路径加载对应的最小法向应变范围,即max((Δεn, α)min);
7) 利用式(23)计算加载路径的fnp.
本文定义的非比例度因子(式(23))是以正弦波加载为例进行分析得出,为说明式(23)的合理性,利用上述步骤,分别计算等效应变范围为1.2%、应变比为
|
图 3 不同相位差下各平面的法向应变范围(三角波) Figure 3 The normal strain range, Δεn, α, of each plane under different phase delays (triangle wave) |
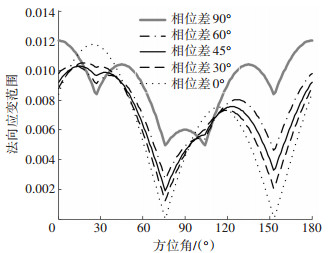
由图 3可见,三角波加载时,相同等效应变、不同相位差下的最小法向应变范围((Δεn, α)min)仍然随着相位差的增大而增大,与正弦波加载时观察到的现象一致.因此,利用(Δεn, α)min描述加载路径的非比例度是合理的.
为进一步验证本文所提方法合理性,利用式(23)计算文献[25]中14种加载路径(具体加载路径形状见文献[25])的非比例度因子,并将计算值与测量值的对比列于图 4.由图 4可见,所提方法可以较好的计算加载路径的非比例度因子.

|
图 4 非比例度因子计算值与测量值的对比 Figure 4 Measured fnp vs. predicted fnp |
选用文献[25-26]中S460N钢和304不锈钢在不同加载路径下稳态应力-应变响应的试验数据来验证所建循环塑性本构模型的预测精度和可靠性.
2.1 S460N钢试验数据取自文献[26].整个试验在室温下进行,为控制应变加载试验,应变比λ(=γa/εa)等于
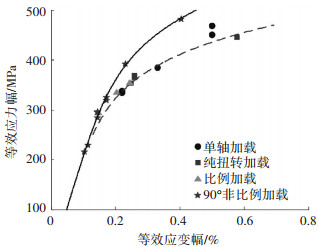
图 6显示的是非比例圆路径和比例加载路径(包括单轴和纯扭转加载)下,S460N钢的等效应力-等效应变关系.由图 6可见,非比例加载路径下S460N钢存在附加强化现象.根据附加强化系数αnp的定义(式(13)),由图 6可以确定S460N钢的αnp为0.3.利用式(23)计算得到各加载路径下的fnp见表 1.
|
图 6 比例(包括单轴和纯扭转)和非比例加载下S460N钢的多轴循环力学行为[26] Figure 6 Multiaxial cyclic behavior of S460N steel under proportional (including uniaxial and torsional) and non-proportional loadings[26] |
| 表 1 各加载路径下的fnp Table 1 Value of fnp for each loading path |
不同加载路径下S460N钢稳态循环应力-应变响应的试验结果与预测结果的比较见图 7.由图 7可见不同加载路径下,模型的预测结果与试验结果吻合较好,表明通过引入非比例度因子和附加强化系数来反映材料的非比例附加强化效应是合理的.

|
图 7 S460N钢稳态应力-应变响应试验结果与预测结果的比较(εa=0.173% and γa=0.3%) Figure 7 Experimental vs. calculated stress responses for S460N steel (εa= 0.173% and γa= 0.3%) |
试验数据取自文献[25].与S460N钢类似,整个试验也在室温下进行,为控制应变加载试验,应变比λ等于
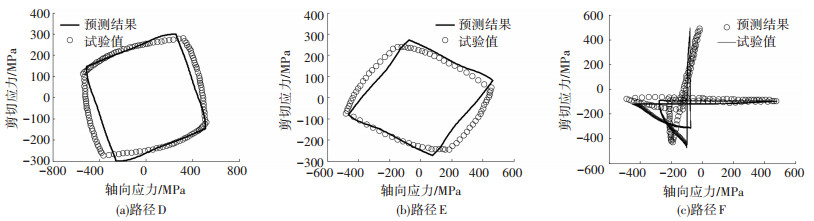
对于图 5中加载路径D、E和F,304不锈钢稳态循环应力-应变响应的试验结果与预测结果的比较见图 8.由图 8可见,不同加载路径下,模型的预测结果与试验结果吻合良好.
|
图 8 304不锈钢稳态应力-应变响应试验结果与预测结果的比较(εa=0.4% and γa=0.695%) Figure 8 Experimental vs. calculated stress responses for S460N steel (εa= 0.4% and γa= 0.695%) |
大量试验结果表明,在相同等效应变下,构件非比例加载路径下的疲劳寿命要远小于比例加载路径下的疲劳寿命.从微观角度讲,非比例加载路径下应变主轴连续旋转,导致多滑移系开动,阻碍材料内部形成稳定的位错结构,从而产生非比例附加强化现象,这是导致非比例加载下疲劳寿命降低的主要原因[28].因此,为合理的预测构件的疲劳寿命,在模拟材料的应力-应变响应时,需要考虑非比例附加强化效应的影响.本文所建模型中,通过引入非比例度因子和附加强化系数,从加载路径和材料本身两个方面来考虑非比例附加强化效应的影响.
由前面的分析可知,在计算过程中,本文利用S460N钢多轴圆路径和比例加载路径下的试验结果来计算材料的附加强化系数.在缺少试验数据的情况下,为了仍然可以利用所建模型模拟材料的稳态应力-应变响应,需要建立附加强化系数的估算公式. Borodii等[29]通过分析25种材料的试验结果,建立如下经验公式来计算材料的附加强化系数:
| $ {\text{lg}}\left| {{\alpha _{np}}} \right| = 0.705\left( {\frac{{{S_u}}}{{{S_y}}} - 1} \right) - 1.22. $ | (26) |
式中Su和Sy分别是材料的抗拉强度和屈服强度.由上式可知,在缺少试验数据时,利用材料的抗拉强度和屈服强度就可以对附加强化系数进行估算.
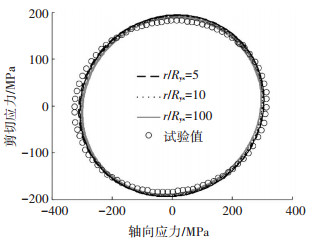
由式(11)可见,在背应力演化方程中含有一个材料常数r.为研究r取值对本构模型计算结果的影响,利用圆路径加载下S460N钢的试验结果对所建模型进行分析(见图 9).分析过程中,材料屈服面半径Rys(=
|
图 9 r取值对路径C预测结果的影响 Figure 9 The predicted stress response for Path C, showing the influence of r |
材料手册中容易查找到材料的常规力学参量,但是对于循环强度系数K′和循环应变硬化指数n′,很多材料在手册中并未给出.为解决这一问题,Li等[30]利用121种合金钢的试验数据建立了K′和n′的估算公式:
| $ K' = \left\{ \begin{array}{l} 1.21{S_u} + 555,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{S_u}/{S_y} \ge 1.4;\\ 3.63 \times {10^{ - 4}}{\left( {{S_u}} \right)^2} + 0.68{S_u} + 570,\;\;1.2 < {S_u}/{S_y} < 1.4;\\ 2.16 \times {10^{ - 4}}{\left( {{S_u}} \right)^{2.1}} + 728,\;\;\;\;\;\;\;\;\;\;\;\;\;{S_u}/{S_y} \le 1.4. \end{array} \right. $ | (27) |
| $ n' = \frac{{\lg \left( {K'} \right) - \lg \left[ {0.089{{\left( {1 + \psi } \right)}^{1.35}}S_u^{1.35}{{\left( { - \frac{{0.002}}{{\ln \left( {1 + \psi } \right)}}} \right)}^{0.216}} + 120} \right]}}{{\lg 500}}. $ | (28) |
式中ψ为材料的断面收缩率.
根据上述估算公式(式(26)~(28)),在缺少试验数据时,仅仅利用常规力学参量即可由本文所建本构模型来模拟多轴载荷下材料的稳态循环应力-应变响应,便于工程应用.
4 结论1) 建立一个新的考虑非比例附加强化效应的稳态循环塑性本构模型.应用新模型时,仅仅需要3个独立的常规力学参量和2个疲劳参数.而且,在缺少疲劳试验数据时,结合文献[29-30]中的估算公式,仅仅利用常规力学参量便可由所建模型来模拟多轴载荷下材料的稳态循环应力-应变响应,便于工程应用.
2) 新模型中引入的非比例度因子和附加强化系数,从加载路径和材料本身两个方面来考虑非比例附加强化效应对稳态循环应力-应变响应的影响.
3) 利用最小法向应变范围,提出一种计算加载路径非比例程度的新方法.该方法克服了利用载荷间相位差无法描述相位差相同,应变比不同时加载路径非比例程度的不足.
需要说明的是,所建模型适用于塑性不可压金属材料小变形范围内的稳态循环应力-应变响应特性分析,并假设材料为各向同性且处于自然无变形状态.
| [1] |
SHAMSAEI N, FATEMI A. Effect of microstructure and hardness on non-proportional cyclic hardening coefficient and predictions[J].
Materials Science and Engineering A, 2010, 527: 3015-3024.
DOI: 10.1016/j.msea.2010.01.056 |
| [2] |
SOCIE D, MARQUIS G.
Multiaxial fatigue[M]. Warrendale: Society of Automotive Engineers Inc., 2000: 53-67.
|
| [3] |
ARMSTRONG P J, FREDERICK C O. A mathematicalrepresentation of the multiaxial Bauschinger effect: RD/B/N731[R]. Berkely: Central Electricity Generating Board, Berkely Nuclear Laboratories, 1966.
|
| [4] |
CHABOCHE J L. On some modifications of kinematic hardening to improvethe description of ratcheting effects[J].
International Journal of Plasticity, 1991, 7: 661-678.
DOI: 10.1016/0749-6419(91)90050-9 |
| [5] |
杨显杰, 高庆, 孙训方. 循环塑性双曲面多轴本构模型研究[J].
力学学报, 1993, 25(5): 569-574.
YANG Xianjie, GAO Qing, SUN Xunfang. A study on twosurface multiaxial constitutive model of cyclic plasticity[J]. Acta Mechanica Sinica, 1993, 25(5): 569-574. |
| [6] |
DORING R, HOFFMEYER J, SEEGER T, et al. A plasticity model for calculating stress-strain sequences under multiaxial nonproportional cyclic loading[J].
Computational Materials Science, 2003, 28: 587-596.
DOI: 10.1016/j.commatsci.2003.08.015 |
| [7] |
JIANG Y, SEHITOGLU H. Modeling of cyclicratcheting plasticity, Part Ⅰ: Development of constitutive relations[J].
Journal of Applied Mechanics, 1996, 63: 720-725.
DOI: 10.1115/1.2823355 |
| [8] |
TANAKA E. A nonproportionality parameter and a cyclic viscoplastic constitutive model taking into account amplitude dependence and memory effects of isotropic hardening[J].
European Journal of Mechanics A/Solids, 1994, 13: 155-173.
|
| [9] |
KHUTIA N, DEY P P, HASSAN T. An improved nonproportional cyclic plasticity model for multiaxial low-cycle fatigue and ratchetingresponses of 304 stainless steel[J].
Mechanics of Materials, 2015, 91: 12-25.
DOI: 10.1016/j.mechmat.2015.05.011 |
| [10] |
CHEN X, JIAO R. Modified kinematic hardening rule for multiaxial ratcheting prediction[J].
International Journal of Plasticity, 2004, 20: 871-898.
DOI: 10.1016/j.ijplas.2003.05.005 |
| [11] |
MEGGIOLARO M A, WU H, CASTRO J T P. Nonproportional hardening models for predicting mean and peak stress evolution in multiaxial fatigue using Tanaka's incremental plasticity concepts[J].
International Journal of Fatigue, 2016, 82: 146-157.
DOI: 10.1016/j.ijfatigue.2015.07.027 |
| [12] |
GATES N R, FATEMI A. A simplified cyclic plasticity model for calculating stress-strain response under multiaxial nonproportional loading[J].
European Journal of Mechanics A/Solids, 2016, 59: 344-355.
DOI: 10.1016/j.euromechsol.2016.05.001 |
| [13] |
ZHANG J, JIANG Y. Constitutive modeling of cyclic plasticity deformation of a pure polycrystalline copper[J].
International Journal of Plasticity, 2008, 24(10): 1890-1915.
DOI: 10.1016/j.ijplas.2008.02.008 |
| [14] |
WU H, MEGGIOLARO M A, CASTRO J T P. Computational implementation of a non-linear kinematic hardening formulation for tension-torsion multiaxial fatiguecalculations[J].
International Journal of Fatigue, 2016, 91: 304-312.
DOI: 10.1016/j.ijfatigue.2016.01.005 |
| [15] |
SHAMSAEI N, FATEMI A, SOCIE D F. Multiaxial cyclic deformation and non-proportional hardening employing discriminating load paths[J].
International Journal of Plasticity, 2010, 26: 1680-1701.
DOI: 10.1016/j.ijplas.2010.02.006 |
| [16] |
KRISHNA S, HASSAN T, NACEURI B, et al. Macro versus micro-scale constitutive models in simulating proportional and nonproportional cyclic and ratcheting responses of stainless steel 304[J].
International Journal of Plasticity, 2009, 25: 1910-1949.
DOI: 10.1016/j.ijplas.2008.12.009 |
| [17] |
ITOH T, KAMEOKA M, OBATAYA Y. A new model for describing astable cyclic stress-strain relationship under nonproportional loading on activation state of slip systems[J].
Fatigue & Fracture of Engineering Materials and Structures, 2004, 27: 957-967.
DOI: 10.1111/j.1460-2695.00818.x |
| [18] |
KOWALEWSKI Z L, SZYMCZAK T, MACIEJEWSKI J. Material effects during monotonic-cyclic loading[J].
International Journal of Solids and Structures, 2014, 51: 740-753.
DOI: 10.1016/j.ijsolstr.2013.10.040 |
| [19] |
MADRIGAL C, NAVARRO A, CHAVES V. Biaxial cyclic plasticity experiments and application of a constitutive model forcyclically stable material behaviour[J].
International Journal of Fatigue, 2016, 83: 240-252.
DOI: 10.1016/j.ijfatigue.2015.10.019 |
| [20] |
JIANG Y, KURATH P. Characteristics of the Armstrong Frederick type plastic models[J].
International Journal of Plasticity, 1996, 12(3): 387-415.
DOI: 10.1016/S0749-6419(96)00013-7 |
| [21] |
LI J, LI C W, QIAO Y J, et al. Fatigue life prediction for some metallic materials under constant amplitude multiaxial loading[J].
International Journal of Fatigue, 2014, 68: 10-23.
DOI: 10.1016/j.ijfatigue.2014.06.009 |
| [22] |
ELLYIN F, X IA, Z. A rate-independent constitutive model for transient nonproportional loading[J].
Journal of Mechanics of Physics and Solids, 1989, 37: 71-91.
DOI: 10.1016/0022-5096(87)90005-6 |
| [23] |
KANAZAWA K, MILLER K J, BROWN M W. Low cycle fatigue under out of phase loading conditions[J].
Journal of Engineering Materials and Technology, 1977, 99: 222-228.
DOI: 10.1115/1.3443523 |
| [24] |
BENALLAL A, MARQUIS D. Constitutive equations for non-proportional cyclic elasto-viscoplasticity[J].
Journal of Engineering Materials and Technology, 1987, 109: 326-336.
DOI: 10.1115/1.3225985 |
| [25] |
ITOH T, SAKANE M, OHNAMI M, et al. Non-proportional low cycle fatigue criterion for type 304 stainless steel[J].
Journal of Engineering Materials and Technology, 1995, 117: 285-292.
DOI: 10.1115/1.2804541 |
| [26] |
HOFFMEYER J, DORING R, SEEGER T, et al. Deformation behaviour, short crack growth and fatigue lives under multiaxial nonproportional loading[J].
International Journal of Fatigue, 2006, 28: 508-520.
DOI: 10.1016/j.ijfatigue.2005.05.014 |
| [27] |
JIANG Y, OTT W, BAUM C, et al. Fatigue life predictions by integrating EVICD fatigue damage model and an advanced cyclic plasticity theory[J].
International Journal of Plasticity, 2009, 25: 780-801.
DOI: 10.1016/j.ijplas.2008.06.007 |
| [28] |
朱正宇, 何国球, 张卫华, 等. 非比例载荷下多轴疲劳微观机理的研究进展[J].
同济大学学报(自然科学版), 2006, 34(11): 1510-1514.
ZHU Zhengyu, HE Guoqiu, ZHANG Weihua, et al. Recent advances in micromechanisms of multiaxial fatigue under nonproportional loading[J]. Journal of Tongji University (Natural Science), 2006, 34(11): 1510-1514. DOI: 10.3321/j.issn:0253-374X.2006.11.018 |
| [29] |
BORODII M V, SHUKAEV S M. Additional cyclic strain hardening and its relation to materialstructure, mechanical characteristics, and lifetime[J].
International Journal of Fatigue, 2007, 29: 1184-1191.
DOI: 10.1016/j.ijfatigue.2006.06.014 |
| [30] |
LI J, ZHANG Z P, LI CW. An improved method for estimation of Ramberg-Osgood curves of steels from monotonic tensile properties[J].
Fatigue & Fracture of Engineering Materials and Structures, 2016, 39: 412-426.
DOI: 10.1111/ffe.12366 |
 2017, Vol. 49
2017, Vol. 49