雷达散射截面[1-4](Radar cross section, RCS)是衡量隐身飞机隐身性能的最主要指标.描述飞机隐身程度的传统方法主要是求取目标的RCS均值,但是此值并不能给出足够充分的信息.为此,外场缩比模型测试[5]和电磁仿真软件计算成为当前计算飞机全空域各个角度RCS的两个最主要途径.在忽略测试和仿真环境误差的情况下,目标RCS与视角、频率[6]和极化等密切相关,意味着同一目标在不同条件下所测RCS是存在差异的,如何准确评价飞机重点角域[7]隐身性能,是目前研究的主要方向.
本文借鉴文献[8-10]中对实测数据进行处理的移动平滑算法,对HH极化和VV极化方式下获取的0°周向RCS数据进行平滑,去除了突兀“毛刺”,从而降低极化引起的起伏误差.并参考文献[11-14]中以雷达探测概率为基础,评估飞机各角域隐身性能的研究方法,对移动平滑处理的RCS数据进行探测概率求解,意图更为全面和客观地评估飞机重点角域的隐身性能.
1 问题描述目标的RCS与视角、频率和极化方式等密切相关,因而导致数据的来源和获取产生较大起伏及误差.尤其是属于快起伏目标的隐身飞机,起伏差异性尤为明显.因此,单纯利用目标的RCS起伏特性很难准确评估飞机各个角域的隐身性能,在此,需要对所测RCS数据进行处理才能达到评估目的.
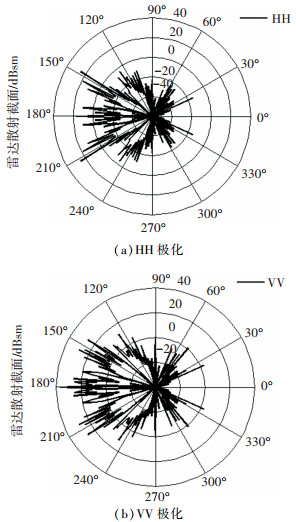
考虑图 1(a)和图 1(b)所示的RCS起伏变化情况. 图 1(a)和图 1(b)分别是某型隐身飞机在水平极化(HH)和垂直极化(VV)模式下,俯仰角为0°的周向散射分布图,照射频率为5.8 GHz.
|
图 1 RCS的周向分布 Figure 1 Circumferential distribution of RCS |
1) 极化方式不同,飞机RCS在周向各个角域的起伏变化分布不同,图 1(a)、(b)中宽角域和窄角域内的RCS分布很不相同,机身尾向和机翼前后缘的“突峰”较多,机身尾向存在一个角域较宽的强散射区,头向是窄角域的弱散射区.在周向范围内的RCS分布变化都很敏感,存在明显的突兀“毛刺”,
2) 不同极化方式下,机体同一角域的RCS起伏产生误差,很难利用单一极化的RCS起伏描述飞机的隐身性能.且RCS均值只能概括飞机的整体隐身性能,很难给出可靠的可探测性结果,故无法为实战提供有效的战场信息.
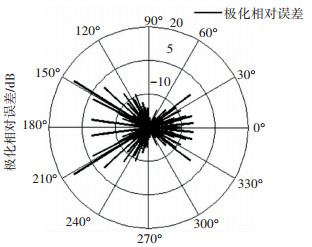
3) 定义水平极化和垂直极化的差值为RCS的极化相对误差,即Δσ=σHH-σVV,具体如图 2所示.
|
图 2 RCS极化相对误差 Figure 2 Relative error of RCS polarization |
图 2中RCS极化相对误差的存在给飞机各个角域部位的隐身性能评估带来困难.因此,利用传统的移动平滑算法能够通过相应的平滑与滤波处理减少极化相对误差的影响,以及单脉冲检测和非相参积累检测能够相对客观地解决隐身飞机的可探测性问题,结合二者能够给出较为客观和可靠的评估结果.
2 移动平滑模型一般地,隐身飞行器的目标RCS经电磁计算获得的测量数据为σi, i=1, 2, …, M,通常可以用多项式(1)表示为
| $ {\sigma _i} = s\left( i \right) + u\left( i \right),\;\;\;\;i = 1,2, \cdots ,M. $ | (1) |
式中: u(i)为零均值等方差相互独立且平稳的白噪声;s(i)是s阶多项式,用一组时间函数的多项式族{sτ(i), τ=0, 1, …, s}的线性组合表示为
| $ s\left( i \right) = \sum\limits_{\tau = 0}^s {{\kappa _\tau }{s_\tau }\left( i \right)} . $ | (2) |
式中: κτ为多项式族的系数,则用矩阵形式表示式(1)为
| $ \mathit{\boldsymbol{\sigma }} = \mathit{\boldsymbol{S\kappa }} + \mathit{\boldsymbol{u}}. $ | (3) |
其中各矩阵向量具体为:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{S}} = {\left( {{s_\tau }\left( 1 \right),{s_\tau }\left( 2 \right), \cdots ,{s_\tau }\left( M \right)} \right)^{\rm{T}}};\\ \mathit{\boldsymbol{\kappa }} = {\left( {{\kappa _0},{\kappa _1}, \cdots ,{\kappa _s}} \right)^{\rm{T}}};\\ \mathit{\boldsymbol{\sigma }} = {\left( {{\sigma _1},{\sigma _2},\cdots,{\sigma _M}} \right)^{\rm{T}}};\\ \mathit{\boldsymbol{u}} = {\left( {{u_1},{u_2},\cdots,{u_M}} \right)^{\rm{T}}}. \end{array} \right. $ | (4) |
将式(3)变换后,可得多项式族的系数.
| $ \mathit{\boldsymbol{\kappa }} = {\left( {{\mathit{\boldsymbol{S}}^{\rm{T}}}\mathit{\boldsymbol{S}}} \right)^{ - 1}}{\mathit{\boldsymbol{S}}^{\rm{T}}}\mathit{\boldsymbol{\sigma }}. $ | (5) |
依据最小二乘法原理求κτ的最小二乘估计,即通过求函数
| $ F = \sum\limits_{i = 1}^M {{{\left( {\sum\limits_{\tau = 0}^s {{\kappa _\tau }{s_\tau }\left( i \right) - {\sigma _i}} } \right)}^2}} . $ | (6) |
使其偏微分方程满足
| $ {\kappa _\tau } = \sum\limits_{i = 1}^M {\frac{{{\sigma _i}{s_\tau }\left( i \right)}}{{\varphi \left( {M,\tau } \right)}}.} $ | (7) |
其中,定义
| $ \hat \sigma \left( i \right) = \sum\limits_{\tau = 0}^s {{\kappa _\tau }{s_\tau }\left( i \right)} . $ | (8) |
计算σi在M+δ(δ为滤波位置点)处的L阶(L≥0的整数)微分的最优线性无偏估计值,得
| $ \hat \sigma _{M + \delta }^{\left( L \right)} = \sum\limits_{\tau = L}^s {{\kappa _\tau }s_\tau ^{\left( L \right)}\left( {M + \delta } \right)} = \sum\limits_{\tau = L}^s {\sum\limits_{i = 1}^M {\frac{{{\sigma _i}{s_\tau }\left( i \right)s_\tau ^{\left( L \right)}\left( {M + \delta } \right)}}{{\varphi \left( {M,\tau } \right)}}} } . $ | (9) |
令
| $ {W_{M - i}} = \sum\limits_{\tau = L}^s {\frac{{{s_\tau }\left( i \right)s_\tau ^{\left( L \right)}\left( {M + \delta } \right)}}{{\varphi \left( {M,\tau } \right)}}} . $ | (10) |
当等时间采样间隔为t时,
| $ {W_{M - i,t}} = \frac{1}{{{t^L}}}\sum\limits_{\tau = L}^s {\frac{{{s_\tau }\left( i \right)s_\tau ^{\left( L \right)}\left( {M + \delta } \right)}}{{\varphi \left( {M,\tau } \right)}}} . $ | (11) |
| $ \hat \sigma _{M + \delta }^{\left( L \right)} = \sum\limits_{i = 1}^M {{W_{M - i}}{\sigma _i}.} $ | (12) |
此处,δ<0是数据平滑的基本条件,在动态测量里,主要利用中心平滑技术求取该值.即δ=-(M-1)/2.
式(12)中,WM-i是平滑处理的权系数,其与最优无偏估计值多项式族的阶数s、微分阶数L、采样点的个数M以及滤波位置点δ有关.当上述变量在给定情况下,WM-i是能够被确定的变量,当作一个“窗口”.
移动平滑就是采取固定数量的观测值设计“窗口”尺寸,然后通过移动“窗口”的方法对整个观测数据进行平滑处理.从算法建立过程可以看出,移动平滑即是对测量得到的目标RCS数据进行s阶多项式拟合,进而获得权系数WM-i, …, W0,以作为平滑“窗口”存贮起来.在对后面的处理中,针对一个“新”的测量数据和“旧”的M-1个数据,只需把存贮的多项式权系数和相应的数据平滑处理序列相乘相加,即能完成对新数据的估值,以此顺时移动“窗口”,曲线全部拟合为止,即可得到目标RCS数据的平滑处理结果,其拟合值表达式为
| $ \hat \sigma _{M + \delta }^{\left( L \right)}\left( {M + \delta + l} \right) = \sum\limits_{i = 1}^M {{W_{M - i}}{\sigma _{i + l}}} . $ | (13) |
式中l为移动步长,是整数.当l=1时,为逐点移动法.
3 探测概率模型幅度变化、相位未知的起伏信号的最佳检测方式是单脉冲检测和非相参积累检测[14].对于隐身飞机一类的快起伏目标,回波的起伏将明显破坏相邻回波信号的相位相参性,故一般不采用相参积累检测.文献[11, 15]对起伏目标单脉冲检测和非相参积累检测均进行了较为详细的建模和仿真.
3.1 单脉冲检测雷达接收到的回波信号中,只有噪声信号时,起伏目标回波信号的包络r(t)的概率密度函数分布为
| $ p\left( r \right) = r\exp \left( { - \frac{{{r^2}}}{2}} \right). $ | (14) |
则虚警概率为
| $ {P_{{\rm{fa}}}} = \int_{{V_{\rm{T}}}}^\infty {p\left( r \right){\rm{d}}r} = \exp \left( { - \frac{{V_{\rm{T}}^2}}{2}} \right). $ | (15) |
检测门限VT为
| $ {V_{\rm{T}}} = \sqrt {2\ln \frac{1}{{{P_{{\rm{fa}}}}}}} . $ | (16) |
存在目标信号时,目标回波信号的包络r(t)的概率密度分布为
| $ p\left( r \right) = r\exp \left( { - \frac{{{r^2} + \varepsilon }}{2}} \right){I_0}\left( {r\sqrt \varepsilon } \right). $ | (17) |
式中:ε=2E/N0是信号的峰值信噪比,E为信号总能量,N0为噪声信号的单边功率谱密度,I0(x)为零阶第一类修正贝塞尔函数.则探测概率为
| $ {P_{\rm{d}}} = \int_{{V_{\rm{T}}}}^\infty {r\exp \left( { - \frac{{{r^2} + \varepsilon }}{2}} \right){I_0}\left( {r\sqrt \varepsilon } \right){\rm{d}}r} . $ | (18) |
起伏目标的回波信号幅度A是具有某种概率密度分布p(A)的函数变量.目前,多采用SwelingⅠ-Ⅳ分布模型、对数正态分布模型以及卡方分布模型等对p(A)近似拟合,但始终无法准确描述快起伏目标的回波起伏特点,本文将直接采用目标RCS的实测原始数据的概率密度分布进行数值计算,以保留回波信号的真实性.由此,探测概率进一步深化为
| $ {P_{\rm{d}}} = \int_0^\infty {\int_{{V_{\rm{T}}}}^\infty {p\left( A \right)r\exp \left( { - \frac{{{r^2} + \varepsilon }}{2}} \right){I_0}\left( {r\sqrt \varepsilon } \right){\rm{d}}r{\rm{d}}A} } . $ | (19) |
非相参积累在包络检波后进行,通常使用平方律检波器进行检波.对第n个脉冲的平方律检波器的输出正比于器输入的平方,则定义平方律检波器输出端的变量yn为
| $ \left\{ \begin{array}{l} {y_n} = \frac{{r_n^2}}{2};\\ {\varepsilon _n} = \frac{{2{E_n}}}{{{N_0}}}. \end{array} \right. $ | (20) |
式中: εn为每个脉冲的峰值信噪比,En是第n个脉冲的信号总能量.根据式(17)中回波信号的包络r(t)的概率密度函数,可知变量yn概率密度函数为
| $ p\left( {{y_n}} \right) = p\left( {{r_n}} \right)\left| {\frac{{{\rm{d}}{r_n}}}{{{\rm{d}}{y_n}}}} \right| = \exp \left( { - \left( {{y_n} + \frac{{{\varepsilon _n}}}{2}} \right)} \right){{\rm{I}}_0}\left( {\sqrt {2{y_n}{\varepsilon _n}} } \right). $ | (21) |
对N个脉冲的非相参积累的实现可表示为
| $ x = \sum\limits_{n = 1}^N {{y_n}} . $ | (22) |
由于各个随机变量yn是相互独立的,变量x的概率密度函数为
| $ \begin{array}{l} p\left( x \right) = p\left( {{y_1}} \right) * p\left( {{y_2}} \right) * \cdots * p\left( {{y_n}} \right) = \\ {\left( {\frac{{2x}}{{N{\varepsilon _n}}}} \right)^{\frac{{N - 1}}{2}}}{I_{N - 1}}\sqrt {2N{\varepsilon _n}} \exp \left( { - x - \frac{{N{\varepsilon _n}}}{2}} \right). \end{array} $ | (23) |
其中IN-1是N-1阶修正贝塞尔函数,算子*表示卷积.则非相参积累检测的探测概率为
| $ \begin{array}{l} {P_{\rm{d}}} = \int_{{V_{\rm{T}}}}^\infty {p\left( x \right){\rm{d}}x} = \int_{{V_{\rm{T}}}}^\infty {{{\left( {\frac{{2x}}{{N{\varepsilon _n}}}} \right)}^{\frac{{N - 1}}{2}}}{I_{N - 1}}\left( {\sqrt {2N{\varepsilon _n}} } \right)} \\ \;\;\;\;\;\;\;\;\exp \left( { - x - \frac{{N{\varepsilon _n}}}{2}} \right){\rm{d}}x. \end{array} $ | (24) |
式中: VT为检测门限,由虚警概率Pfa确定,与幅度起伏特性无关.
设εn=0,即可得到只有噪声时回波信号的概率密度函数,根据虚警概率的定义最终得到Pfa与门限V′T的关系式为
| $ {P_{{\rm{fa}}}} = \int_{{V_{\rm{T}}}}^\infty {p\left( x \right){\rm{d}}x} = \int_{{V_{\rm{T}}}}^\infty {\frac{{{x^{N - 1}}\exp \left( { - x} \right)}}{{\left( {N - 1} \right)!}}{\rm{d}}x} $ | (25) |
至此,联合式(20)~式(25)即可完整解决起伏回波信号的非相参脉冲积累的检测问题.
3.3 探测概率误差利用上述探测概率模型,定义探测概率误差ΔPd,一是检验HH极化和VV极化的RCS数据在求取探测概率后,存在的差异性程度;二是检验求解移动平滑后,两种RCS极化相对误差所引起的雷达探测概率的具体差异,以使平滑处理和飞机的可探测性能达到最佳.鉴于此,将两种极化RCS数据的雷达探测概率的差值求取绝对值后,定义探测概率误差函数为
| $ \Delta {P_{\rm{d}}} = \left| {P_{\rm{d}}^{{\rm{HH}}} - P_{\rm{d}}^{{\rm{VV}}}} \right|. $ | (26) |
式中: PdHH是HH极化方式下RCS数据的雷达探测概率;PdVV是VV极化方式下RCS数据的雷达探测概率.
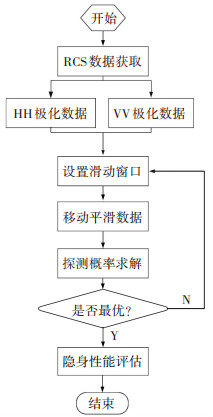
4 仿真分析图 3给出飞机隐身性评估的仿真验证流程.
|
图 3 隐身性能评估的仿真流程图 Figure 3 Simulation process of stealth performance evaluation |
仿真验证流程为:首先,借助电磁软件获取HH极化和VV极化的飞机0°周向RCS数据;其次,设置滑动窗口尺寸,对数据平滑处理;然后,求取平滑数据的非相参积累探测概率,比较分析能否有效评估飞机的可探测性;最后,确定平滑效果最好的窗口尺寸以及最佳的非相参积累检测效果,对飞机的隐身性能进行最佳评估。
4.1 移动平滑处理为检验移动平滑模型的可行性,对HH极化和VV极化的0°周向RCS数据进行平滑曲线拟合,平滑窗口W= 1,5,10,15,20,如图 4所示.

|
图 4 不同窗口平滑处理的RCS Figure 4 The smooth RCS of different window |
图 4表明:1)移动平滑能够有效去除RCS数据中的“尖峰”和“毛刺”,HH极化和VV极化的数据拟合曲线随着窗口尺寸的变大而趋于一致;但是窗口尺寸变大,RCS原始数据包含的信息特征失真度将越高,可能会对某些角域的隐身性能造成不客观的评价.因此,选择合适的平滑窗口是隐身性能评价的关键一步;2)根据平滑结果,对飞机的重点隐身角域形成初步的评估.其中,0~60°和300°~360°分别为隐身飞机头向左侧和右侧的重点隐身区域,域内RCS均值小,性能好;60°~120°和240°~300°分别是飞机左侧和右侧的隐身区域,域内RCS起伏误差大,两个突兀“峰值”较明显;120°~165°和195°~240°是飞机左后方和右后方的隐身区域,域内RCS起伏小,均值相对较大;165°~195°是飞机尾向隐身区域,域内隐身较差,突兀峰值RCS大.
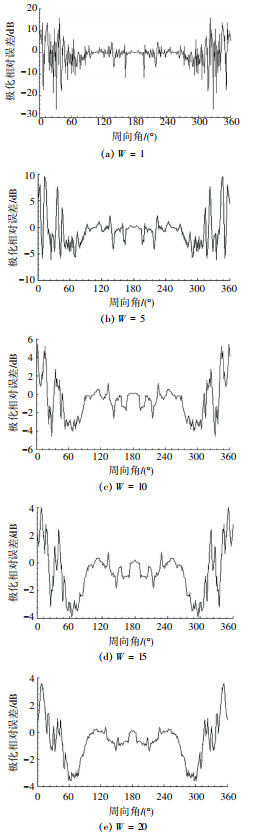
结合相对极化误差定义,图 5(a)~(e)给出了不同平滑窗口处理的RCS极化相对误差结果.
|
图 5 不同窗口平滑处理的RCS极化相对误差 Figure 5 The smooth RCS relative error of different window |
分析图 5可知,移动平滑窗口尺寸越大, RCS极化相对误差的平滑效果越好,W= 1时,HH极化和VV极化所测的数据起伏误差在-40~20 dB范围,而W= 15及W= 20时,RCS极化相对误差的误差范围缩小为-5~5 dB范围.因此,移动平滑能够有效去除“毛刺”,但平滑窗口尺寸不易过大,一是平滑窗口尺寸过大,易使原始数据信息失真,二是窗口过大平滑效果趋于稳定,处理效果减弱.
为减小极化方式对RCS数据的影响,在平滑处理的基础上,主要以雷达探测概率为基础,对飞机各个角域的隐身性能进行评价.依据现役雷达的性能参数,结合防空实战化需求,雷达基本参数设置如表 1所示.
| 表 1 雷达参数设置 Table 1 Radar parameters setting |
根据目标测试数据,可以得到回波信号幅度A的PDF,即p(A).结合表 1所设定的雷达参数,得到给定Pfa和SNR条件下的单脉冲探测概率,目前单脉冲探测概率的积分运算主要依据Marcum和Parl等建立的简单数值算法来近似求解.
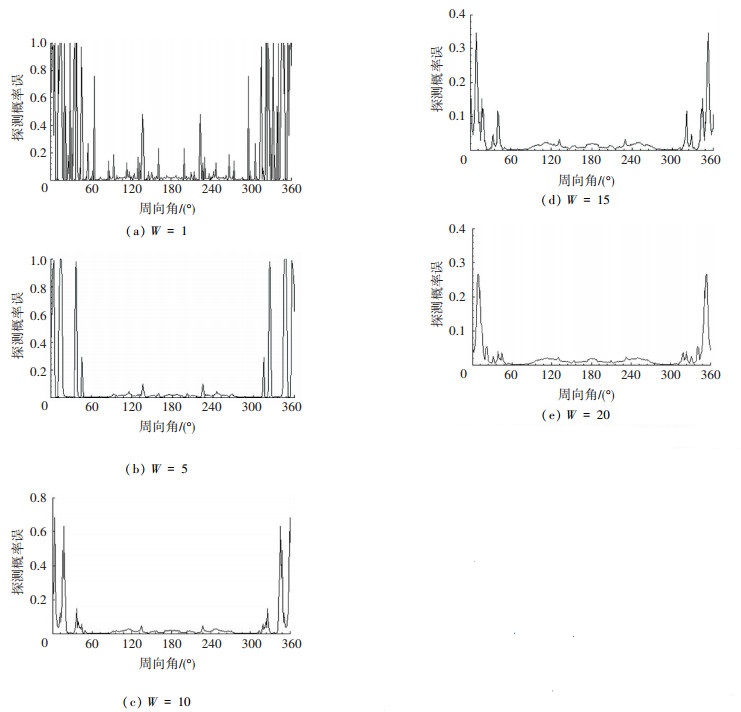
利用HH极化和VV极化不同平滑程度处理的RCS数据,可以得到不同平滑窗口的探测概率误差,图 6(a)~(e)所示,能够有效地显示平滑后RCS极化相对误差的缩减程度以及飞机重点部位的隐身性能.
|
图 6 不同平滑窗口的探测概率误差 Figure 6 The detection probability error of different smooth window |
由图 6(a)~(e)可知,取不同的平滑窗口,得到的探测概率误差差异明显.原始实测数据(W= 1)的RCS极化相对误差明显集中在0~60°和300°~360°,域内探测概率误差起伏较大,因此飞机在这些区域的隐身性能评估将存在较大误差,但随着平滑窗口的增加,误差逐渐减小,不同极化方式的RCS数据经平滑处理后拟合曲线契合度较高,此时对飞机该角域的评估更具说服性.此外,移动平滑需重点考虑原始RCS数据的保真度,不能过度平滑而使飞机重点角域的隐身特性失真.
为此,提出非相参脉冲积累,通过积累检测与移动平滑相结合的方式对HH极化和VV极化的原始实测数据进行处理,评价飞机的隐身性能,力求取得更加客观的结论.
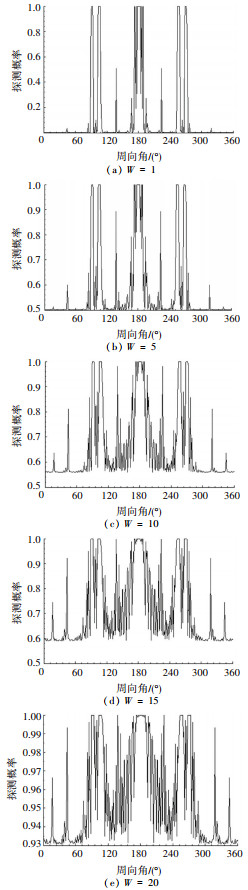
4.3 非相参积累检测依据3.2小节中已经对非相参积累检测原理以及数值近似计算公式.本小节在单脉冲检测的基础上,采用MATLAB编程对脉冲积累数N分别为1,5,15,20,25时HH极化和VV极化的原始实测数据的非相参积累探测概率进行了仿真计算,见图 7(a)~(e)和图 8(a)~(e)所示.
|
图 7 HH极化数据的非相参积累检测 Figure 7 The incoherent integration detection of HH polarization data |
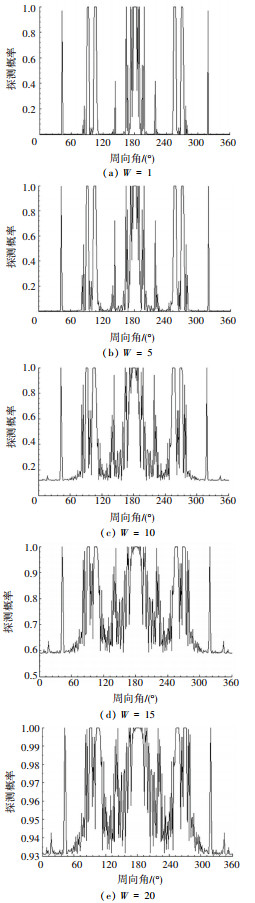
|
图 8 VV极化数据的非相参积累检测 Figure 8 The incoherent integration detection of VV polarization data |
1) 非相参脉冲积累能够显著提高雷达的检测性能.积累脉冲数增加,雷达探测概率整体提升,但不改变飞机各个角域的可探测性能,能将HH极化和VV极化产生的探测概率误差更加明显的呈现出来.例如,单脉冲检测(N= 1)时,0~90°和270°~360°的角域范围内,雷达探测性能较低,域内探测概率的差异性无法有效呈现;而非相参脉冲积累(N= 10, 15, 20)时,雷达探测性能提高,0~90°和270°~360°的域内探测概率差异性能够有效体现.
2) 非相参积累检测能够将探测概率误差最大化,有助于移动平滑过程中准确判断拟合曲线的误差,进而客观评价飞机的隐身性能.
通过对HH极化和VV极化的原始实测RCS数据的单脉冲探测概率和非相参积累探测概率进行仿真求解,发现移动平滑算法能够有效去噪,雷达探测概率亦能够评估的飞机隐身性能.基于此,需要求解移动平滑窗口尺寸和非相参积累脉冲数的最优组合解(W, N).
4.4 滑动窗口及非相参积累脉冲的最优组合解最优组合解的求解原则为:一是使平滑处理的RCS极化相对误差范围最小,但前提是原始数据反映的信息不能失真,从新添加的图 5可以看出,滑动窗口到达一定尺寸时,平滑处理效果基本保持不变,而原始数据反映的信息特征消失.二是为评估飞机的隐身性能,非相参积累探测概率较小或较大,都会使某些角域的探测概率基本降为0或达到100%以上,很难反映各个角域可探测性能的差异,因此,最好的非相参积累探测概率应该是尽可能将各个角域的概率误差信息都能反映出来.只要两者的处理效果达到最优,才能对各个角域的隐身性能进行合理的评估.
用数学模型表示上述约束条件为:
| $ {\text{s.t}} = \left\{ \begin{array}{l} \min \left( {\Delta {P_{\rm{d}}}} \right),\\ \min \left( {\Delta \sigma } \right),\\ W \in \left[ {1,20} \right],\\ N \in \left[ {1,20} \right]. \end{array} \right. $ | (27) |
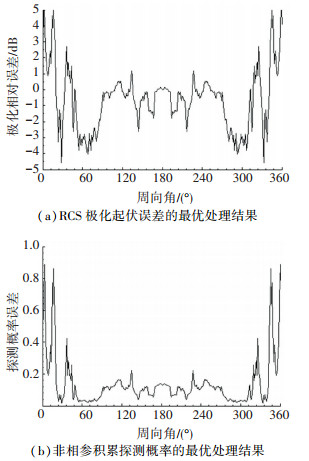
在3小节中,滑动窗口W=1, 5, 10, 15, 20, 非相参积累脉冲数N=1, 5, 10, 15, 20.暂不考虑滑动窗口尺寸和非相参积累脉冲数的具体设置时,共W×N=25种组合.因此,采用遍历比较法进行仿真求解,得到的最优组合解为(10, 10).其中,相应的RCS极化相对误差和探测概率误差如图 9(a)、(b).
|
图 9 最优处理的误差结果 Figure 9 Error results of the optimal processing |
分析图 9可知,移动平滑窗口W= 10时,极化引起的起伏误差已经缩减至-5~5 dB范围,有效去除了突兀“毛刺”和“峰值”的影响;非相参积累脉冲数N= 10时,飞机周向的雷达探测概率误差较小,除0~20°和340°~360°角域误差概率几乎在50%以上,其他角域的误差概率均在40%以下,有效提高了雷达对飞机的可探测性以及衡量评估的可行性.
基于此,对原始实测的不同极化RCS数据进行最优处理,得到仿真结果如图 10(a)、(b)所示,分别是HH极化和VV极化周向范围内重点角域的雷达探测概率.
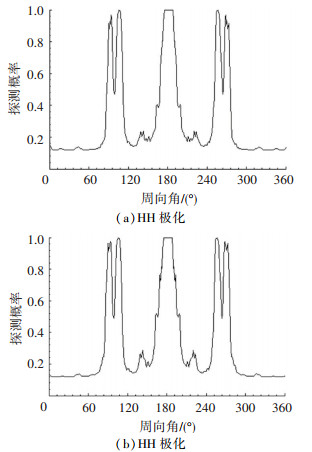
|
图 10 最优处理得到的雷达探测概率 Figure 10 Radar detection probability of the optimal processing |
比较图 7(c)和图 8(c)中N= 10时,HH极化和VV极化的飞机周向的雷达探测概率,并结合图 10可知:
1) 图 7和图 8中,HH极化和VV极化的雷达探测概率在同一角域区别很大,起伏明显,“毛刺”较多,无法准确评估飞机各个角域的可探测性;相比图 10,经过最优处理,HH极化和VV极化的雷达探测概率在各个角域基本趋于吻合,能够得到最佳的评估效果.
2) 图 10可知,飞机在侧向75°~120°、240°~285°以及150°~210°的角域范围内,RCS起伏较大,探测概率高,易被雷达搜索发现;在0~60°、300°~360°以及120°~150°和210°~240°角域范围内,RCS起伏小,隐身性能较好,雷达发现的概率小.
3) 移动平滑能够有效去噪,减小极化引起的起伏影响;而雷达探测概率能够有效衡量飞机的可探测性,给出信息量足够的评估效果.
5 结论本文结合移动平滑算法和探测概率模型,提出了一种评估不同极化方式下飞机重点角域隐身性能的可行方法.利用移动平滑算法处理RCS数据降低了极化引起的相对起伏误差,并求取了雷达探测概率以衡量飞机的可探测性能.所得结论如下:
1) 移动平滑能够有效降低RCS极化相对误差,但窗口尺寸过小,不足以去除“毛刺”;窗口尺寸过大,RCS拟合曲线失真,失去平滑价值.
2) 雷达探测概率能够提供完整信息以衡量飞机重点角域的可探测性能.且非相参积累脉冲越高,可探测性能越好,更能有效评估飞机的隐身性能;同时也提高了极化引起的探测概率误差,大大制约了评估价值和方法的可靠性.
3) 移动平滑窗口和非相参积累脉冲的最优组合解为(10,10)时,飞机隐身性能的评估效果达到最佳.
| [1] |
PERSSON B, NORSELL M. On modeling RCS of aircraft for flightsimulation[J].
IEEE Antennas & Propagation Magazine, 2014, 56(4): 34-43.
|
| [2] |
YUE Kuizhi, LIU Wenlin, LI Guanxiong, et al. Numerical simulation of RCS for carrier electronic warfare airplanes[J].
Chinese Journal of Aeronautics, 2015, 28(2): 545-555.
DOI: 10.1016/j.cja.2015.01.0041000-9361 |
| [3] |
YUE Kuizhi, GAO Yong, LI Guanxiong, et al. Conceptual design and RCS performance research of shipborne early warning aircraft[J].
Journal of Systems Engineering and Electronics, 2014, 25(6): 968-976.
DOI: 10.1109/JSEE.2014.00111 |
| [4] |
岳奎志, 贾忠湖, 姬金祖, 等. 舰载电子战飞机RCS特性数值模拟[J].
系统工程与电子技术, 2014, 36(5): 852-858.
YUE Kuizhi, JIA Zhonghu, JI Jinzu, et al. Numerical simulation on the RCS of carrier-based electronic warfare aircraft[J]. Systems Engineering and Electronics, 2014, 36(5): 852-858. DOI: 10.3969/j.issn.1001-506X.2014.05.07 |
| [5] |
肖志河, 高超, 白杨, 等. 飞行器雷达隐身测试评估技术及发展[J].
北京航空航天大学学报, 2015, 41(10): 1873-1879.
XIAO Zhihe, GAO Chao, BAI Yang, et al. Aircraft radar stealth test and evaluation technology and progress[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(10): 1873-1879. DOI: 10.13710/j.bh.1001-5965.2015.0220 |
| [6] |
刘战合, 黄沛霖, 武哲. 飞行器目标频率响应散射特性[J].
航空学报, 2009, 30(4): 643-648.
LIU Zhanhe, HUANG Peilin, WU Zhe. Frequency response scattering characteristic of aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(4): 643-648. |
| [7] |
岳奎志, 孙聪, 姬金祖. 双立尾对战斗机隐身特性的数值模拟[J].
北京航空航天大学学报, 2014, 40(2): 160-165.
YUE Kuizhi, SUN Cong, JI Jinzu. Numerical simulation on the stealth characteristics of twin-vertical-tails for fighter[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(2): 160-165. |
| [8] |
郑奕, 张晓林. 移动平滑算法在无人机遥测数据处理中的应用[J].
北京航空航天大学学报, 2003, 29(4): 350-353.
ZHENG Yi, ZHANG Xiaolin. Moving-polynomial smoother algorithms for telemetry flight-test data processing of pilotless helicopter[J]. Journal of Beijing University of Aeronautics and Astronautics, 2003, 29(4): 350-353. |
| [9] |
陆正刚, 王恒亮, 张宝安. 车轮实测型面数据平滑处理方法[J].
振动.测试与诊断, 2013, 33(6): 943-949.
LU Zhenggang, WANG Hengliang, ZHANG Baoan. Methods for smoothing of wheel measured profile data[J]. Journal of Vibration, Measurement & . Diagnosis, 2013, 33(6): 943-949. |
| [10] |
高自娟, 朱玉全, 陈耿. 基于变尺度滑动窗口的流数据聚类算法[J].
计算机应用研究, 2011, 28(2): 551-553.
GAO Zijuan, ZHU Yuquan, CHEN Geng. Streaming data cluster algorithm based on changeable sliding window[J]. Application Research of Computers, 2011, 28(2): 551-553. DOI: 10.3969/j.issn1001-3695.2011.02.040 |
| [11] |
陈世春, 黄沛霖, 姬金祖. 从探测概率的角度评价飞机的隐身性能[J].
航空学报, 2015, 36(4): 1150-1161.
CHEN Shichun, HUANG Peilin, JI Jinzu. Evaluating aircraft's stealth performance from the perspective of detection probability[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(4): 1150-1161. DOI: 10.7527/S1000-6893.2014.0187 |
| [12] |
YI Mingxiu, WANG Lifeng, HUANG Jun. Active cancellation analysis based on the radar detectionprobability[J].
Aerospace Science and Technology, 2015, 46: 273-281.
DOI: 10.1016/j.ast.2015.07.018 |
| [13] |
ALJAROUDI A, FHAN F, AKINTURK A, et al. Probability of detection and false detection for subsea leakdetection systems: model and analysis[J].
Journal of Failure Analysis and Prevention, 2015, 15(6): 873-882.
DOI: 10.1007/s11668-015-0033-6 |
| [14] |
LI Ying, WU Zhe, HUANG Peilin, et al. A new method for analyzing integrated stealth ability of penetration aircraft[J].
Chinese Journal of Aeronautics, 2010, 23(2): 187-193.
DOI: 10.1016/S1000-9361(09)60203-X |
| [15] |
MAHAFZA B R, ELSHERBENI A Z. 雷达系统设计MATLAB仿真[M]. 朱国富, 黄晓涛, 黎向阳, 等, 译. 北京: 电子工业出版社, 2009: 52-82.
MAHAFZA B R, ELSHERBENI A Z. MATLAB simulations for radar system design[M]. ZHU Guofu, HUANG Xiaotao, LI Xiangyang, et al, translated. Beijing: Publishing House of Electronics Industry, 2009:52-82. |
 2017, Vol. 49
2017, Vol. 49


