引用本文

王星星, 叶继红. 多层强边柱冷成型钢结构体系抗震性能分析[J]. 哈尔滨工业大学学报, 2017, 49(12): 16-23. DOI: 10.11918/j.issn.0367-6234.201701036. 复制到剪切板

WANG Xingxing, YE Jihong. Seismic analysis on mid-rise cold-formed steel structure with reinforced end studs[J]. Journal of Harbin Institute of Technology, 2017, 49(12): 16-23. DOI: 10.11918/j.issn.0367-6234.201701036. 复制到剪切板

基金项目

国家自然科学基金(51538002)

作者简介

王星星(1986—)，女，博士研究生;
叶继红(1967—)，女，教授，博士生导师

通信作者

叶继红, jhye@cumt.edu.cn

文章历史

收稿日期: 2017-01-09

Abstract Full text Figures/Tables PDF

多层强边柱冷成型钢结构体系抗震性能分析

王星星¹, 叶继红²

1. 东南大学土木工程学院，南京 210096;
2. 深部岩土力学与地下工程国家重点实验室(中国矿业大学)，江苏徐州 221116

收稿日期: 2017-01-09

基金项目: 国家自然科学基金(51538002)

作者简介: 王星星(1986—)，女，博士研究生;
叶继红(1967—)，女，教授，博士生导师

通信作者: 叶继红, jhye@cumt.edu.cn

摘要: 多层强边柱冷成型钢结构能够促进低层冷成型钢结构向多层住宅结构体系的发展.为了分析多层强边柱冷成型钢住宅结构体系在地震作用下的动力特性，本文提出了该类结构的主要抗侧构件强边柱冷成型钢组合墙体可以考虑节点实际连接性能的简化计算模型，进而得到整体结构抗震计算模型；根据作者前期开展的墙体抗剪试验结果并结合国外规范，提出此类结构在地震作用下的侧向变形验算指标；对整体结构进行抗震性能研究.结果表明：考虑节点连接的等代拉压杆模型能够准确预测此类结构的实际受力特性；将1/300和1/75分别作为此类结构在多遇和罕遇地震作用下的层间位移角限值是安全可靠的；在9度罕遇地震作用下，此类结构不会发生倒塌破坏；进行此类结构设计时，不宜采用两个方向刚度差异过大的抗剪墙体组合，同时应重点加强结构沿墙体开洞率较大方向的墙体抗剪强度；在特别高烈度地区进行此类结构设计时，应兼顾墙体抗剪强度和墙体边柱的竖向承载能力，避免结构因墙体边柱的压屈破坏而导致整体结构失效.

关键词: 多层冷成型钢结构方钢管混凝土强边柱抗侧设计指标抗震性能简化计算

Seismic analysis on mid-rise cold-formed steel structure with reinforced end studs

WANG Xingxing¹, YE Jihong²

1. School of Civil Engineering, Southeast University, Nanjing 210096, China;
2. State Key Laboratory for Geomechanics & Deep Underground Engineering (China University of Mining and Technology), Xuzhou 221116, Jiangsu, China

Abstract: Mid-rise cold-formed steel (CFS) structure with reinforced end studs can promote the development of mid-rise CFS residential buildings from low-rise ones. To analyze the dynamic characteristics of mid-rise CFS residential structures with reinforced end studs under earthquakes, a simplified calculation model of CFS shear wall with reinforced end studs, which is the main lateral load-bearing structural component of the structure, was proposed. The proposed model could consider the real behavior of beam-column joint, and then the seismic calculation model of the whole structure was further obtained. Lateral design objectives for the structure under earthquake were proposed according to abroad specification and previous shear wall test results that performed by authors, and seismic analysis on a mid-rise CFS structure with reinforced end studs was carried out. The results show that equivalent-bracing model considering the mechanical behavior of beam-column joint can precisely predict the seismic performance of the structure. It is safe and reliable that 1/300 and 1/75 being taken as the elastic and inelastic storey drift limits of the structure under frequent and severe earthquake, respectively. Mid-rise CFS structure with reinforced end studs will not collapse under severe earthquake with a degree of 9. It is not suitable to adopt shear wall combination with large difference in stiffness between two directions, and the shear strength of the walls along the direction with larger opening rate should be strengthened emphatically. In areas of particularly high seismicity, both shear strength of the wall and vertical bearing capacity of end studs should be taken into account to avoid overall failure, which is caused by end studs' buckling.

Key words: mid-rise CFS structure concrete-filled rectangular steel tube column lateral design objectives seismic performance simplified calculation

冷成型钢房屋住宅结构具有轻质高强、环保节能、施工快捷等优点.在北美、欧洲、日本等地，三层以下别墅及公寓类型房屋已为人们所接受并广泛使用^[1].中国人口众多，土地资源紧缺，将冷成型钢住宅结构从低层发展到多层具有现实意义.

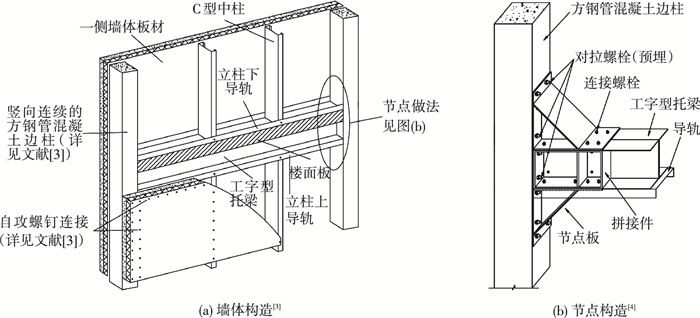
冷成型钢组合墙体是冷成型钢结构的主要承重及抗侧构件.传统双拼C型边柱组合墙体无论是抗剪强度还是竖向稳定性均难以满足多层住宅结构的要求，不能直接应用于多层冷成型钢结构^[2].为此，作者提出了以竖向连续布置的方钢管混凝土柱作为墙体边柱的强边柱冷成型钢组合墙体，并在梁柱连接位置设置具有一定弯矩传递能力的加强型节点(见图 1)^[3-4].试验研究结果表明，方钢管混凝土边柱改善了传统双拼C型边柱底部的压屈破坏，保证了结构的竖向稳定性，同时解决了传统冷成型钢结构的上、下层不连续问题，提高了结构整体抗侧性能，同时由于柱内混凝土对螺钉倾斜的抑制作用，墙体本身抗剪强度明显提高；此外，由加强型节点连接的强边柱冷成型钢组合墙体骨架在加载后期形成了除墙板外的第二道安全防线，大大提高了多层冷成型钢房屋住宅结构的安全性能^[5].

图 1 典型强边柱冷成型钢组合墙体 Figure 1 Typical CFS shear wall with reinforced end studs

考虑到足尺模型试验成本高、周期长，精细化有限元分析方法又具有建模过程繁琐、计算耗时等缺点，目前国内外在冷成型钢整体结构抗震性能方面的主要研究手段大多为等代拉压杆法，且结构简化分析模型将节点的连接等效为理想铰接，而考虑节点真实连接条件下建立冷成型钢结构整体分析模型的研究目前尚属空白^[6].此外，基于性能的抗震设计在混凝土结构和普通钢结构中的应用已经过漫长的考验，其在冷成型钢结构中的应用还有待进一步研究^[7].因此，研究能反映冷成型钢整体结构实际受力特性的简化计算方法，并给出结构抗震设计指标是将多层强边柱冷成型钢房屋住宅结构体系推广应用的前提.

本文首先对强边柱冷成型钢组合墙体的简化计算模型展开研究，根据文献[5]试验结果对该模型进行验证，为多层强边柱冷成型钢整体结构的简化计算提供基础.其次，根据作者前期开展的墙体抗剪试验结果并结合现有规范，提出地震作用下多层强边柱冷成型钢房屋住宅结构的侧向变形验算指标.最后，对多层强边柱冷成型钢房屋住宅结构进行抗震计算，分析影响结构抗震性能的关键因素，并初步考察此类结构在大震作用下的抗倒塌能力.

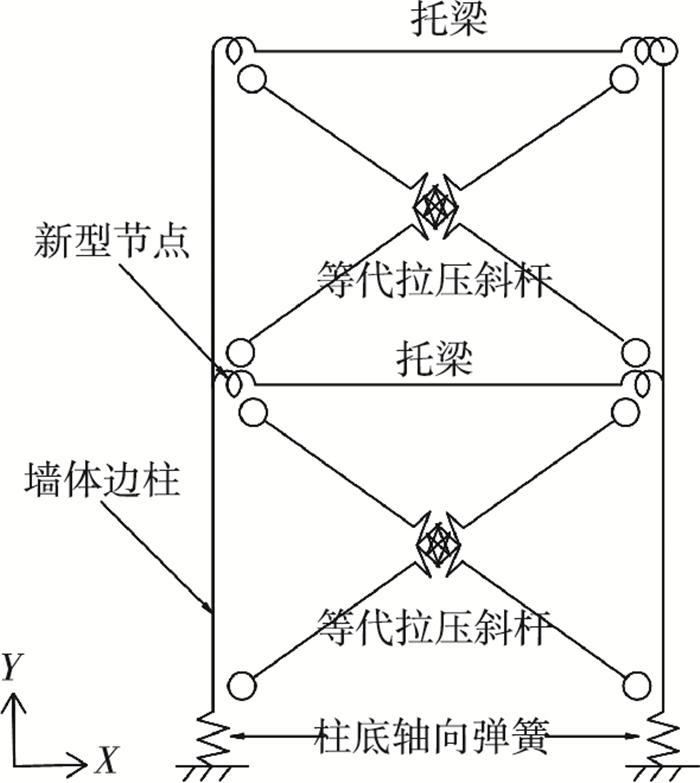
1 强边柱冷成型钢组合墙体简化计算模型 1.1 简化方法

图 2为强边柱冷成型钢组合墙体简化计算模型.该模型基于以下简化方法：

图 2 强边柱冷成型钢组合墙体简化计算模型 Figure 2 Simplified calculation model of CFS shear wall with reinforced end studs

1) 将各层楼面托梁简化为刚性杆，并在楼面托梁与方钢管混凝土边柱的连接节点设置转动弹簧以考虑节点连接性能.其中，方钢管混凝土边柱采用杆单元模拟，按等效抗弯刚度原则定义其材性；转动弹簧的弯矩-转角本构根据节点连接性能试验确定.

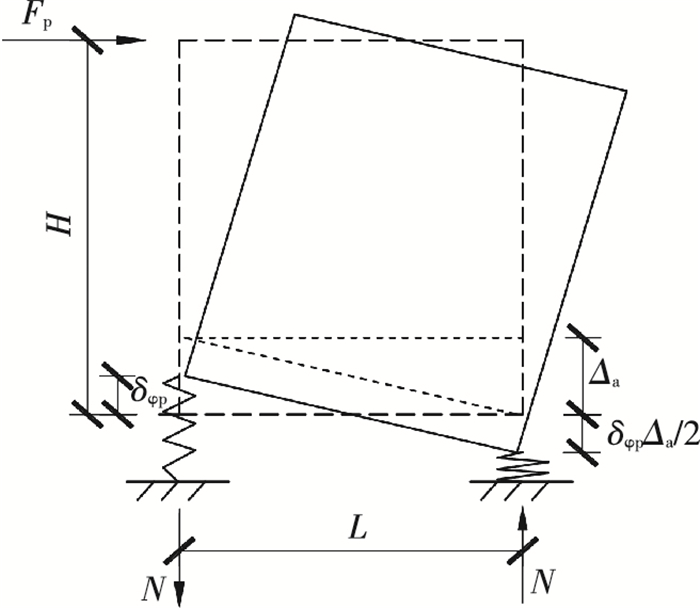
2) 由于边柱与基础之间采用抗拔连接件有效连接，故约束边柱底部的转动自由度和X向平动自由度，通过设置沿Y向的轴向弹簧以考虑方钢管混凝土边柱可能发生的压屈破坏.其中，柱底轴向弹簧的拉压刚度(k_Spring)根据墙体抗剪承载力F_p及其对应的墙体竖向相对变形Δ_a确定，见图 3和式(1)；如果方钢管混凝土边柱未发生压屈破坏，则其轴向弹簧的拉压刚度取为无穷大.

图 3 柱底轴向弹簧刚度的确定 Figure 3 Stiffness determination of the axial spring

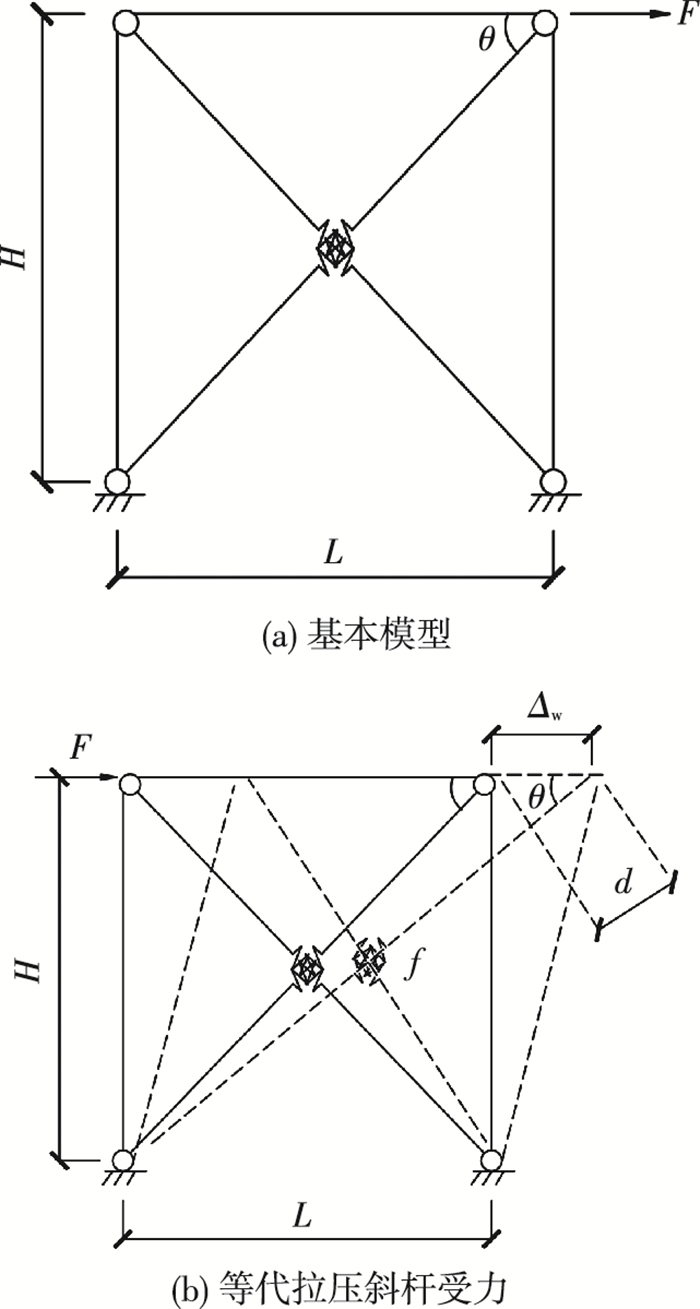
3) 将各层墙板及中柱耦合简化为带有非线性弹簧单元的等代拉压斜杆，拉压斜杆主要抵抗水平荷载，非线性弹簧单元的恢复力特性根据墙体荷载-位移曲线按式(2)、(3)进行转换，见图 4.其中，强边柱冷成型钢组合墙体的荷载-位移曲线可采用足尺抗剪试验、精细化有限元模拟^[8]及分段函数滞回模型^[9]等方法确定.

$ {{k}_{\rm{Spring}}}=\frac{2{{F}_{\rm{p}}}H}{L{{\mathit{\Delta }}_{\rm{a}}}~}, $

(1)

图 4 冷成型钢组合墙体受力示意 Figure 4 Force diagram of CFS shear wall

式中：Δ_a为墙体两侧竖向相对变形；H、L分别为墙体高度和宽度.

$ f=F/2\rm{cos } \ \theta, $

(2)

$ d={{\mathit{\Delta }}_{\rm{w}}}\cdot \rm{cos}~\theta . $

(3)

式中：f、d为非线性弹簧单元的轴力和变形，分别与墙体的荷载F和位移Δ_w对应；θ为等效拉压斜杆与托梁之间的夹角.

1.2 算例验证

采用Opensees有限元程序建立墙体简化计算模型，对文献[5]中两层强边柱冷成型钢组合墙体试件进行计算.其中，试件宽度为3.6 m，各层墙体高度为3 m；边柱截面为□140 mm×140 mm×1.5 mm，内灌C_b20细石混凝土；各层楼面托梁为两根背靠背的冷弯U型钢(截面规格U260 mm×50 mm×1.5 mm)，通过在腹板上用双排自攻螺钉连接成工字型截面.

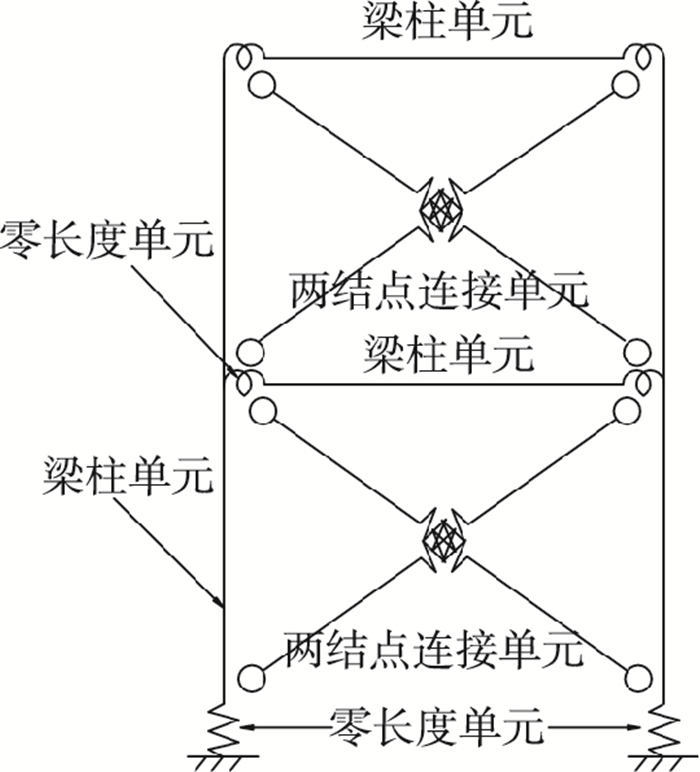
如图 5所示，选用两结点连接单元(two node link element)模拟等代拉压斜杆；方钢管混凝土边柱和各层楼面托梁均由弹性梁柱单元(elastic beam-column element)模拟；节点转动弹簧和边柱底部轴向弹簧均由零长度单元(zero-Length element)模拟.等代拉压斜杆的恢复力特性和节点转动弹簧的弯矩-转角本构均通过Pinching4材料模型^[8]定义，且考虑到墙体和节点的正反向加载曲线基本对称，仅定义正向加载的恢复力特性参数.表 1为墙体简化计算模型中各单元输入参数取值.其中，非线性弹簧单元的骨架曲线输入参数根据文献[2]中单层140型墙体抗剪试验结果按式(2)、(3)确定；根据楼板平面内刚性假定，将楼面托梁的弹性模量放大10 000倍以模拟刚性杆；由于试验过程中墙体边柱基本未出现压屈现象，因此将柱底弹簧的轴向刚度取为无穷大.

图 5 墙体简化计算模型 Figure 5 Simplified calculation model of the wall

表 1 墙体简化计算模型各单元输入参数 Table 1 Input parameters of the simplified calculation model

对模型施加边界约束后，采用倒三角制度施加水平循环位移，位移级差与文献[5]试验加载制度一致，取为5 mm.图 6为水平荷载作用下，两层墙体各层剪力-位移滞回曲线和底层剪力-位移骨架曲线的简化计算结果与试验结果对比.可以看出，墙体简化模型的各层剪力-位移滞回曲线和底层剪力-位移骨架曲线的计算结果能充分体现出墙体的非线性特性和滞回特征.

图 6 双层墙体荷载-位移曲线 Figure 6 Load-displacement curves of the wall

表 2列出了底层墙体简化计算结果与试验结果^[5]对比，包括抗剪强度Q_1s、屈服剪力Q_1y、屈服位移Δ_1y、墙体位移达到1/300层高时对应的剪力Q₃₀₀以及剪力达到峰值时，各层墙体顶部相对于地面的水平位移Δ_wm.对比得出，计算结果与试验值的相对误差在9%以内，说明本文墙体简化计算模型中各单元类型选取合理、参数定义准确，可以准确预测多层冷成型钢结构体系的实际受力特性.

表 2 两层墙体简化计算结果与试验结果对比 Table 2 Comparisons between the calculated and test results of the wall

2 地震作用下多层强边柱冷成型钢房屋住宅结构侧向变形验算指标

中国JGJ 227—2011《低层冷弯薄壁型钢房屋建筑技术规程》规定，冷成型钢房屋每个主轴方向的水平荷载可根据对应方向上各有效抗剪墙的抗剪刚度大小按比例分配，楼面和屋面通过构造保证其在自身平面内具有足够的刚度^[10].因此，本文假定冷成型钢结构楼面为刚性楼面，当抗剪墙体在建筑平面、竖向分布均匀时，不考虑地震作用下平面扭转效应，同一楼层各剪力墙层间位移相同，并应满足以下变形要求：

1) 多遇水平地震作用下抗侧墙体的弹性层间位移角θ_e应满足：

$ {{\theta }_{\rm{e}}}=\frac{{{Q}_{\rm{e}}}}{{{K}_{\rm{e}}}H}\le [{{\theta }_{\rm{e}}}]. $

(4)

式中：Q_e和K_e分别为多遇水平地震作用下各抗侧墙体的层间总剪力和总抗侧刚度；H为层高；[θ_e]为多遇水平地震作用下弹性层间位移角限值.

作者前期开展的强边柱冷成型钢组合墙体抗剪试验研究结果表明^[2]，墙体剪切变形达到1/300层高时的水平荷载F₃₀₀平均为抗剪承载力F_p的64.5%，该值与墙体荷载-位移骨架曲线由线性向非线性转变的拐点处荷载(约0.6 F_p)十分接近，且平均低于屈服荷载约15.3%，墙体仍处于弹性阶段.因此，本文建议将强边柱冷成型钢组合墙体在多遇地震作用下的层间位移角限值[θ_e]取为1/300 rad.

2) 罕遇水平地震作用下抗侧墙体的弹塑性层间位移角θ_p应满足：

$ {{\theta }_{\rm{p}}}=\frac{{{Q}_{\rm{p}}}}{{{K}_{\rm{p}}}H}\le [{{\theta }_{\rm{p}}}]. $

(5)

式中:Q_p和K_p分别为罕遇水平地震作用下各抗侧墙体的层间总剪力和总抗侧刚度；[θ_p]为罕遇水平地震作用下弹塑性层间位移角限值.

根据文献[2]试验结果，对强边柱冷成型钢组合墙体水平力下降至峰值的85%时的位移角进行统计分析，得到墙体的极限位移角均值为1/55 rad.由于冷成型钢结构在材料、构件和结构体系等方面与常规钢结构不同，故无法直接套用其弹塑性变形限值.因此，本文参照日本规范《薄板輕量形鋼造建築物設計の手引き》^[11]对传统冷成型钢结构的弹塑性变形限值规定，充分考虑强边柱冷成型钢组合墙体较之普通双拼C型边柱组合墙体对冷成型钢结构抗倒塌能力的提升，建议将强边柱冷成型钢组合墙体在罕遇地震作用下的弹塑性层间位移角限值[θ_p]取为1/75 rad.

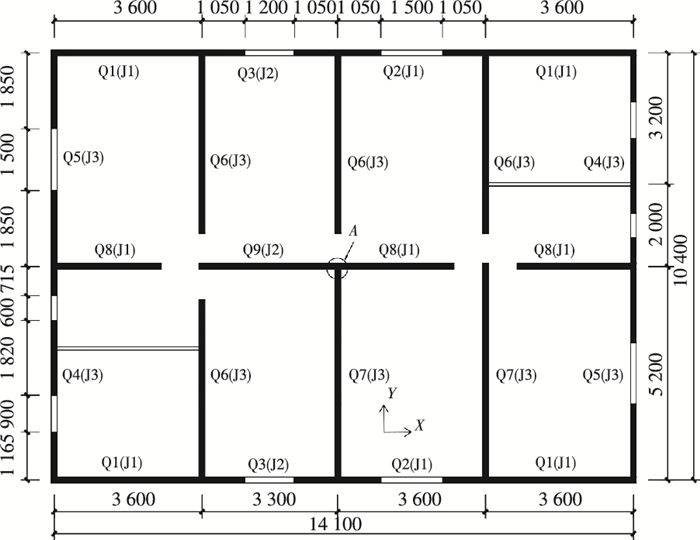
3 多层强边柱冷成型钢房屋住宅结构抗震性能分析 3.1 结构概况

某6层冷成型钢结构住宅，平面尺寸为14.1 m×10.4 m，层高3 m.标准层平面见图 7，各层墙体尺寸及开洞情况一致.抗剪墙体(Q1~Q9)的边柱均为140型方钢管混凝土柱，且方钢管混凝土柱与楼面托梁导轨之间设置加强型梁柱节点.结构采用能够保证平面内刚性的新型组合楼盖^[12]：托梁截面尺寸为255 mm×50 mm×15 mm×1.5 mm，托梁导轨截面尺寸为260 mm×50 mm×1.5 mm，吊顶采用石膏玻镁板.屋盖做法同楼盖，楼盖、屋盖、内外墙及隔墙均采用50 mm岩棉保温层，立柱间距和楼盖托梁间距均为600 mm.

图 7 标准层平面(虚线表示非承重隔墙) Figure 7 Dwelling plan view (Dotted line for a non-load-bearing partition)

各墙体构造及其非线性弹簧单元恢复力特性输入参数见表 3.由于构造相同，抗剪墙体Q₁和Q₂的恢复力特性参数根据文献[2]试验结果确定，如1.2节所述；其余抗剪墙体的恢复力特性参数按分段函数滞回模型方法^[9]确定；不考虑隔墙抗剪作用.

表 3 各墙体构造及非线性弹簧单元恢复力特性输入参数 Table 3 Configurations and input parameters of each shear wall

墙体编号	中柱型号	b×h/m	d₁~d₄/mm	f₁~f₄/kN	r_d, r_f, u_f	a_{K1, 2}, a_{K3, 4}, a_{K, limit}	a_{D1, 2}, a_{D3, 4}, a_{D, limit}	a_{F1, 2}, a_{F3, 4}, a_{F, limit}
Q1	C140^c	—	2.8, 6.2, 23.6, 39.2	32.9, 54.5, 82.4, 70.0	0.1, 0.25, 0.1	0.55, 1.5, 0.55	0.5, 1.5, 0.1	0.5, 1.5, 0.1
Q2	C140	1.5×1.5	3.8, 13.0, 27.8, 44.4	28.6, 55.8, 71. 5, 60.7	0.1, 0.25, 0.05	0.5, 1.1, 0.65	0.45, 1.5, 0.15	0.4, 1.5, 0.2
Q3	C140	1.2×1.5	3.7, 12.5, 26.9, 106.0	27.2, 53.1, 68.0, 4.8	0.1, 0.25, 0.05	0.45, 1.5, 0.85	0.5, 1.5, 0.1	0.5, 1.5, 0.2
Q4	C140	0.9×1.2 &0.6×1.2	3.9, 10.5, 22.6, 66.6	29.1, 55.9, 72.7, 11.0	0.3, 0.3, 0.05	0.55, 1.3, 0.4	0.45, 1.5, 0.15	0.5, 1.5, 0.1
Q5	C140	1.5×1.5	3.8, 11.0, 21.1, 100.0	30.9, 54.3, 68.1, 5.8	0.1, 0.25, 0.05	0.5, 1.1, 0.65	0.45, 1.5, 0.15	0.4, 1.5, 0.2
Q6	C89 ^c	1.0×2.4	3.1, 7.0, 26.1, 124.1	27.2, 53.1, 68.0, 4.76	0.1, 0.25, 0.05	0.55, 1.5, 0.55	0.5, 1.5, 0.1	0.5, 1.5, 0.2
Q7	C89 ^c	—	3.3, 9.3, 20.0, 59.0	26.4, 50.8, 66.1, 10.0	0.1, 0.2, 0.05	0.55, 1.3, 0.4	0.45, 1.5, 0.15	0.5, 1.5, 0.1
Q8	C140 ^c	1.0×2.4	2.8, 6.2, 19.6, 100.0	33.0, 58.5, 86.3, 5.0	0.1, 0.2, 0.05	0.5, 1.2, 0.75	0.5, 1.5, 0.1	0.5, 1.5, 0.2
Q9	C140	—	2.7, 5.9, 18.9, 96.0	31.4, 55.6, 82.1, 4.8	0.1, 0.25, 0.05	0.45, 1.4, 0.6	0.5, 1.5, 0.1	0.5, 1.5, 0.2
注：墙体编号见图 7；C140型龙骨截面尺寸为140 mm×50 mm×13 mm×1.2 mm，C89型龙骨截面尺寸为89 mm×50 mm×13 mm×0.9 mm，^“c”表示双拼C型柱；墙板布置：Q1~Q5为ALC&玻镁板(BMB)//岩棉//石膏板(GWB)&BMB，Q6~Q9为GWB&BMB//岩棉//GWB&BMB，其中GWB和BMB的厚度均为12 mm，ALC板厚度为50 mm；b和h分别为洞口宽度和高度；其余各符号含义同表 1.

表 3 各墙体构造及非线性弹簧单元恢复力特性输入参数 Table 3 Configurations and input parameters of each shear wall

将各抗剪墙体(Q1~Q9)按照1.1节所述方法进行简化，并按照结构中墙体的实际位置进行集成，可得到如图 8所示的结构空间简化力学模型.其中，各节点弯矩-转角本构的确定方法如1.2节所述，其骨架曲线输入参数具体取值见表 4；节点滞回特性参数取值同表 1；由于试验过程中140型方钢管混凝土边柱基本未出现压屈现象，因此将各抗剪墙体柱底弹簧的轴向刚度取为无穷大.采用刚性面模拟楼板，各层质量以集中质量的形式加在楼板标高处的各柱单元顶端.因此将柱底弹簧的轴向刚度取为无穷大.

图 8 结构空间简化计算模型 Figure 8 The overall calculation model of mid-rise CFS structure

表 4 节点弯矩-转角骨架曲线输入参数 Table 4 Input parameters of joints' moment-rotation skeleton curves

根据美国规范计算自振周期的近似公式计算^[13]，可以得到6层冷成型钢结构(H=18 m)的自振周期

$ \mathit{T}=0.05{{\mathit{H}}^{3/4}}=0.437\ \rm{s}\rm{.} $

(6)

与式(6)相比，简化模型计算所得结构主振型(横向)的自振周期T₁=0.463 s，二者比较接近.

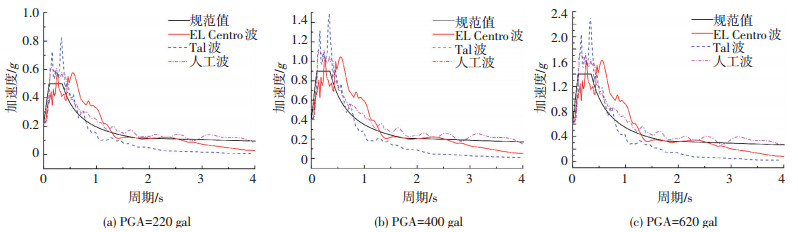
3.2 非线性时程分析 3.2.1 地震波选取

本文非线性时程分析用地震波的详细信息如表 5所示，加速度反应谱如图 9所示.将地震加速度时程按X方向和Y方向输入计算整体结构的响应，研究结构在7度、8度、9度多遇和罕遇地震作用下的变形和内力.参考文献[14]，结构阻尼比取5%.对结构进行弹塑性时程分析之前，将重力荷载代表值以集中荷载的形式施加到各层柱顶节点，作为后续非线性时程分析的初始条件.

表 5 地震波记录 Table 5 Earthquake records

图 9 地震波反应谱(ζ=5%^[14]) Figure 9 Earthquake spectrum(ζ=5%^[14])

3.2.2 结构变形分析

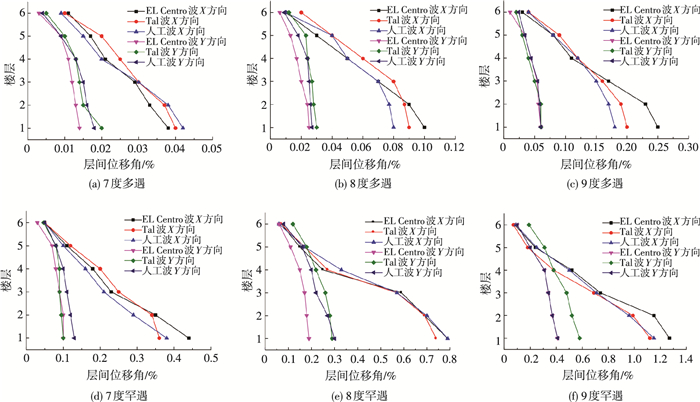
本文从顶点位移和层间位移角两个方面分析结构的变形响应.其中，根据刚性楼面假定，取各楼层4个角点在自由度方向的水平位移平均值代表刚性楼板的水平位移，取相邻楼层水平位移平均值的差值为层间位移计算值.图 10为整体模型在不同地震烈度下各楼层的层间位移角分布，表 6为结构在两个加载方向的顶点位移(图 7中A点)最大值A_m和层间位移角幅值D_m.可以看出，结构层间位移角在不同地震波作用下的总体变化趋势一致，最大层间位移角均发生在结构底层；在多遇地震作用下，结构的层间位移角幅值D_m均小于其变形限值(1/300 rad)要求.对比结构在两个加载方向的响应可以得出，与墙体开洞率较大的X方向相比，结构在抗剪墙分布较密且开洞率较小的Y方向的变形明显偏低.由此可以得出，在此类冷成型钢结构设计过程中应该合理布置抗剪墙体，对于门窗洞口布置较多的地方，应采取加强措施.

图 10 各楼层层间位移角 Figure 10 Story drift ratio

表 6 结构顶点位移最大值A_m/mm和层间位移角幅值D_m /% Table 6 Maximum displacements A_m/mm of point A and the amplitudes D_m /% of story drift ratio

对比表 6中结构在罕遇地震作用下的层间位移角幅值可以得出，结构在X、Y两个方向的层间位移角均满足弹塑性变形限值要求，并远小于国外规范(FEMA 356)^[15]对密肋式结构的抗倒塌变形限值要求，结构不会发生倒塌破坏.由此可以得出，采用1/75 rad作为多层强边柱冷成型钢结构的弹塑性变形限值，结构的强震安全性可得到保证.

3.2.3 墙体内力分析

将各抗剪墙体非线性弹簧单元的最大内力计算值f_pc与表 3中对应屈服强度f₂进行对比，可以得到结构各层抗剪墙体的屈服情况.由于结构在多遇地震作用下未出现墙体屈服，因此本文主要列出结构在7~9度罕遇地震下的抗剪墙体屈服情况，见表 7.对比得出，抗剪墙体的布置情况对结构的抗震性能影响显著；在不同烈度地震作用下，相对于布置较密的Y方向抗剪墙体(Q4~Q7)，结构X方向的抗剪墙体(Q1~Q3、Q8~Q9)内力较大，墙体的屈服数量较多，其中在9度罕遇地震作用下，底层抗剪墙体全部屈服，且随着地震烈度的增加，抗剪墙体屈服现象持续发展至第3层，而结构Y方向的抗剪墙体仍处于弹性阶段.

表 7 非线性弹簧单元最大内力f_pc/kN及1~3层抗剪墙体屈服数量n₁, n₂, n₃ Table 7 The maximum internal force f_pc/kN of nonlinear spring elements and the number n₁, n₂, n₃ of yield shear walls of stories 1~3, respectively

项目内容		EL Centro波			Tal波			人工波
项目内容		7度罕遇	8度罕遇	9度罕遇	7度罕遇	8度罕遇	9度罕遇	7度罕遇	8度罕遇	9度罕遇
f_pc	Q1	50.5	64.7	75.1	52.5	60.2	73.6	54.0	62.9	73.8
	Q2	43.0	54.8	64.2	38.0	47.9	63.1	40.1	51.3	64.2
	Q3	42.4	53.9	63.6	37.5	54.2	61.9	39.7	53.2	58.8
	Q4	20.3	38.3	48.2	23.9	50.7	45.5	24.1	48.4	48.2
	Q5	19.2	36.6	48.0	23.1	43.7	45.3	23.3	47.8	48.0
	Q6	20.4	36.8	42.7	22.7	46.5	43.1	26.4	42.7	42.7
	Q7	18.9	31.4	30.7	26.4	30.1	35.5	18.5	36.2	30.7
	Q8	60.7	68.0	76.1	57.0	63.5	78.0	58.8	69.8	78.5
	Q9	60.1	66.4	75.3	56.8	65.9	77.4	58.2	69.4	77.6
	(n₁, n₂, n₃)	(4, 0, 0)	(10, 6, 0)	(12, 12, 8)	(2, 0, 0)	(10, 6, 0)	(12, 10, 8)	(4, 0, 0)	(10, 6, 0)	(12, 10, 8)

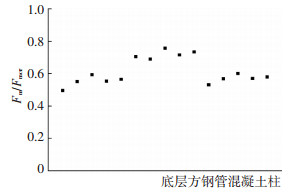
表 8为结构X方向底层抗剪墙体的非线性弹簧单元最大内力f_pc(见表 7)与其屈服强度f₂和峰值力f₃(见表 3)的比值.可以看出，在7度罕遇地震作用下，仅抗剪墙体Q8和Q9达到其屈服强度f₂；当地震烈度达到8度罕遇时，大多数抗剪墙体屈服，且与开洞率较大的抗剪墙体Q2和Q3相比，未开洞或开洞较小的抗剪墙体Q1和Q8、Q9(位于结构X方向)的最大内力f_pc均远远超出其屈服强度f₂.当地震烈度达到9度罕遇时，抗剪墙体全部屈服，结构P-Δ效应加剧，但各抗剪墙体的最大内力f_pc平均低于其峰值力f₃ 8%，未达到其破坏荷载^[16]，结构不会发生倒塌破坏.方钢管混凝土柱的表现也很出色，9度罕遇时，各抗剪墙体边柱的单元内力F_m均未达到其临界压屈荷载F_mcr(见图 11)，边柱未发生压屈破坏，从而形成了除墙板外的第二道安全防线、提高了结构的抗倒塌能力.因此除了合理布置抗剪墙体和加强组合墙体的抗剪强度外，还应提高方钢管混凝土边柱的竖向承载能力，避免结构因墙体边柱的压屈破坏而导致整体结构失效，从而保证整体结构在特大震作用下的安全性.

表 8 X向底层抗剪墙体的非线性弹簧单元内力对比 Table 8 Comparisons of the internal force of bottom shear walls along X directio

图 11 底层方钢管混凝土柱的F_m/F_mcr Figure 11 The ratio of F_m to F_mcr of bottom concrete-filled rectangular steel tube columns

4 结论

1) 考虑节点连接性能的等代拉压杆模型能够准确体现强边柱冷成型钢组合墙体的抗侧性能，可用于预测整体结构的实际受力特性.

2) 采用1/300作为多层冷成型钢房屋住宅结构在多遇地震作用下的层间位移角限值安全可靠；在罕遇地震作用下，采用1/75 rad作为多层冷成型钢结构的弹塑性层间位移角限值，结构的强震安全性可得到保证.

3) 在9度罕遇地震作用下，多层强边柱冷成型钢结构的变形仍满足弹塑性变形限值要求，且底层各抗剪墙体的非线性弹簧单元最大内力平均低于其峰值力8%，同时方钢管混凝土边柱形成了除墙板外的第二道安全防线，结构不会发生倒塌破坏.

4) 进行多层强边柱冷成型钢结构设计时，不宜采用两个方向刚度差异过大的抗剪墙体组合，同时应重点加强结构沿墙体开洞率较大方向的墙体抗剪强度.在特别高烈度地区进行多层冷成型钢房屋住宅结构设计时，应兼顾墙体抗剪强度和墙体边柱的竖向承载能力，避免结构因墙体边柱的压屈破坏而导致整体结构失效，从而保证结构在特别高烈度区的抗倒塌能力.

参考文献

[1]	CHEN Wei, YE Jihong, BAI Yu, et al. Full-scale fire experiments on load-bearing cold-formed steel walls lined with different panels[J]. Journal of constructional steel research, 2012, 79: 242-254. DOI: 10.1016/j.jcsr.2012.07.031
[2]	WANG Xingxing, YE Jinghong. Reversed cyclic performance of cold-formed steel shear walls with reinforced end studs[J]. Journal of constructional steel research, 2015, 113: 28-42. DOI: 10.1016/j.jcsr.2015.05.012
[3]	叶继红, 陈伟. 多层冷成型钢住宅结构: ZL101509274[P]. 2011-05-25.
[4]	叶继红, 王星星, 冯若强, 陈伟. 冷成型钢房屋梁与方钢管混凝土柱的连接节点及连接方法: ZL201410525115. 2[P]. 2016-05-04.
[5]	WANG Xingxing, YE Jihong. Cyclic testing of two-and three-story CFS shear-walls with reinforced end studs[J]. Journal of Construction Steel Research, 2016, 121: 13-28. DOI: 10.1016/j.jcsr.2015.12.028
[6]	FÜLÖP L A, DUBINA D. Performance of wall-stud cold-formed shear panels under monotonic and cyclic loading Part Ⅱ: Numerical modeling and performance analysis[J]. Thin-Walled Structures, 2004, 42: 339-349. DOI: 10.1016/S0263-8231(03)00064-8
[7]	LANDOLFO R, FIORINO L, CORTE G D. Seismic behaviour of sheathed cold-formed structures: physical tests[J]. Journal of structure engineering, ASCE, 2006, 132(4): 570-581. DOI: 10.1061/(ASCE_0733-9445(2006)132:4(570)
[8]	BUONOPANE S G, BIAN G, TUNT H, et al. Computationally efficient fastener-based models of cold-formed steel shear walls with wood sheathing[J]. Journal of constructional steel research, 2015, 110: 137-148. DOI: 10.1016/j.jcsr.2015.03.008
[9]	YE Jihong, WANG Xingxing. Piecewise function hysteretic model for cold-formed steel shear walls with reinforced end studs[J]. Applied sciences, 2017, 7(1): 94. DOI: 10.3390/app7010094
[10]	低层冷弯薄壁型钢房屋建筑技术规程: JGJ 227—2011[S]. 北京: 中国建筑工业出版社, 2011.
[11]	日本钢铁联盟. 薄板輕量形鋼造建築物設計の手引き. [S]. 东京: 技报堂出版社, 2001.
[12]	陈伟, 叶继红, 汪正流. 一种预制装配轻钢耐火组合楼盖结构: ZL201310439815. 5[P]. 2015-07-29.
[13]	American Society of Civil Engineers. Minimum design loads for buildings and other structures: SEI 7-10[S]. Virginia: American Society of Civil Engineers, 2010.
[14]	DUBINA D. Behavior and performance of cold-formed steel-framed houses under seismic action[J]. Journal of Constructional Steel Research, 2008, 64(7): 896-913. DOI: 10.1016/j.jcsr.2008.01.029
[15]	American Society of Civil Engineers. Prestandard and commentary for the seismic rehabilitation of buildings: FEMA 356[S]. Virginia: American Society of Civil Engineers, 2000.
[16]	建筑抗震试验方法规程: JGJ 101—96[S]. 北京: 中国建筑工业出版社, 1997.