2. 鞍钢股份产品发展部, 辽宁 鞍山 114009;
3. 哈尔滨工业大学 土木工程学院, 哈尔滨 150090)
2. Product Development Department, Anshan Iron & Steel, Anshan 114009, Liaoning, China;
3. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China
中国钢结构发展迅速,在民用建筑、工业厂房以及特种结构当中扮演着极为重要的角色.为了实现合理经济的结构优化设计,众多研究人员从结构体系和材料性能入手进行了深入的研究[1].由于钢结构构件内部内力分布不均匀,基于最大受力截面设计的等厚度等截面构件是不合理的,因此,基于单个构件截面的优化设计即是一种简单有效的实现途径.为了满足设计强度要求并减少用钢量,常采用变截面构件,即通过截面尺寸变化实现沿构件长度(跨度)方向上截面设计力矩与采用需求力矩大值相同.现阶段,国内外研究和应用较多的是截面高度和宽度变化的构件,前者主要运用于轻型门式钢架钢梁、吊车梁以及悬臂式雨棚结构当中;后者用于钢框架结构跨度较大的受弯构件当中[2].近年来,纵向变厚度钢板的出现,为变截面构件的实现提供了新的方法.由于钢板自身形式的变革,大大节省了加工安装费用,使其适用范围更广,设计更加灵活.
纵向变厚度钢板(longitudinally profiled steel plate,简称LP钢板)[3-4]厚度沿轧制方向连续变化,用户可根据需求定制各种厚度变化形式和范围,并且在日本和欧洲诸国的造船及桥梁结构中获得大量应用.LP钢板几何尺寸变化以及轧制工艺的特殊性,使得各个厚度处材料性能不同于传统等厚度钢板[5].材料性能以及厚度变化导致的构件各截面惯性矩及强度的不同极大的影响构件受力性能,需要进行深入研究.国外学者对LP钢板的研究开始于20世纪80年代[3],文献[5-6]对LP钢板材料性能进行试验,得到强度随厚度增加非线性下降的规律;文献[7-8]对使用LP钢板构件的极限承载力及受压翼缘局部稳定问题进行了试验研究,建议在桥梁结构主梁翼缘中使用LP钢板;文献[9]采用有限元模拟的方法对三边简支边界条件下单楔形LP钢板的受力性能进行分析,研究其应力分布情况;文献[10]对考虑初始缺陷的LP钢板作翼缘的工字形截面梁的受力性能进行了模拟分析,分析了板件宽厚比变化对极限强度的影响;文献[11-12]采用翼缘增厚型节点(使用LP钢板)与普通节点和翼缘增强型节点的对比试验,对比塑性变形能力;文献[13-15]对在柱脚使用LP钢板的箱型柱进行了循环加载试验,研究厚度变化率及变化长度对抗震性能的影响.目前,国外研究主要由日本学者进行,试验研究较少,多为有限元分析,且缺少有关受弯构件变形性能的研究.中国有关LP钢板的研究仍处于起步阶段,限制了LP钢板的应用与推广.
本文通过对2根LP钢板作翼缘的焊接工型截面梁和2根等厚度钢板作翼缘的焊接工型截面梁进行变形性能试验研究,探究简支边界条件下翼缘厚度变化和不同内力分布对应的厚度变化形式(单点加载和两点加载)对构件变形性能的影响,着重研究构件荷载-位移关系.将试验结果与ANSYS分析结果进行对比,验证有限元模型的正确性,为进一步参数化分析和变形设计提供依据.
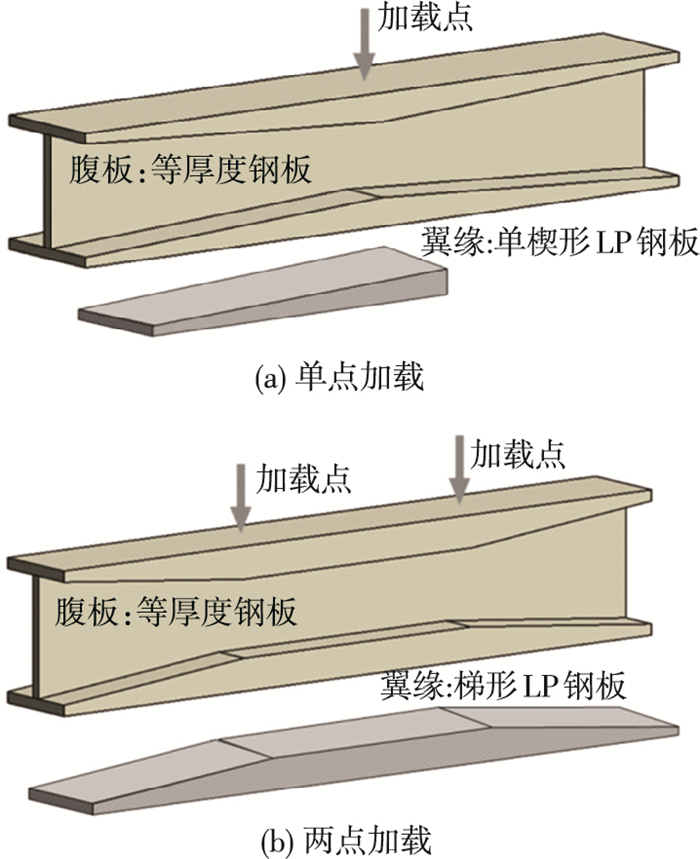
1 试验概况 1.1 试件设计翼缘纵向变厚度工型截面梁采用LP钢板作翼缘,根据梁的内力分布,设计翼缘厚度形状,单点加载和两点加载情况下翼缘纵向变厚度工型截面简支梁见图 1.
|
图 1 翼缘纵向变厚度工型截面简支梁示意 Figure 1 Diagram of I-section beams with LP flanges |
试件为2根翼缘纵向变厚度工型截面梁(BS-1、BD-1)与2根等厚度工型截面梁(BS-2、BD-2):BS-1(两块单楔形LP板对称焊接翼缘)和BS-2在跨中施加集中荷载,用钢量基本相同,BS-1跨中截面全截面屈服荷载提高37.88%;BD-1(梯形LP板翼缘)和BD-2施加两点对称集中荷载,最大受力截面尺寸相同,BD-1用钢量节省9.59 %.试件编号及实测尺寸如表 1所示,其中,L为试件的实际长度,取上下翼缘测量长度的平均值;L0为梁跨度;Lb为两点加载纯弯段长度;B为翼缘宽度,取试件纵向5个测量结果的平均值;H为截面高度,取左、右两端测量结果的平均值;t为板件厚度,取5个测量结果的平均值;α为翼缘厚度变化率.为保证加载过程中支座夹持稳固,在梁跨度方向上两端各增加200 mm延伸段;在支座及加载点处设置加劲肋,厚度均为12 mm.
| 表 1 构件实测尺寸及用钢量 Table 1 Measured sizes and steel volumes of test specimens |
试验所用材料为鞍钢生产的Q345GJC等级纵向变厚度钢板及相同等级的等厚度钢板,其中所用变厚度钢板见图 1.根据GB/T 228—2002《金属材料室温拉伸试验方法》和GB/T 2975—1998《钢及钢产品力学性能试验取样位置及试样制备》中的相关规定,在清华大学结构实验室内进行常温拉伸试验,为了解LP钢板板件性能随厚度变化趋势并确定强度范围,取3个代表厚度沿垂直于轧制方向取样(试件本身厚度变化可忽略),每组取3~4个试件,试验结果见表 2.LP1为试件BS-1翼缘钢板,LP2为试件BD-1翼缘钢板,P1、P2分别为腹板钢板和等厚度翼缘钢板,其中,E为弹性模量,fy为屈服强度,fu为抗拉强度;由于试件采用80 mm标距非比例试样,由GB/T 17600.1—1998《钢的伸长率换算》换算得到比例试样断后伸长率A.可以看出,LP钢板不同厚度处强度不同,随着厚度增加而减小,且强度高于同等厚度等厚度钢板;部分试验值超过YB 4104—2000《高层建筑结构用钢板》的规定范围.
| 表 2 钢板拉伸试验结果 Table 2 Tensile test results of steel plates |
为了使有限元模型更加接近实际试件,在试验开始前采用文献[16-17]中的方法分别测量整体几何初始缺陷和局部几何初始缺陷,具体测量结果如表 3所示,符号含义同前.本文均匀选取7个点或者截面进行测量,前者取偏离两端截面中心相连所成纵轴线方向距离的最大值,后者取偏离翼缘和腹板理论平面距离的最大值.可见,几何初始缺陷满足GB 50205—2001《钢结构工程施工质量验收规范》的要求(翼缘板垂直度≤B/100且不应大于3,腹板≤Hw/200,整体弯曲矢高≤L/100且不应大于10 mm).
| 表 3 构件几何初始缺陷 Table 3 Geometric initial imperfection of specimens |
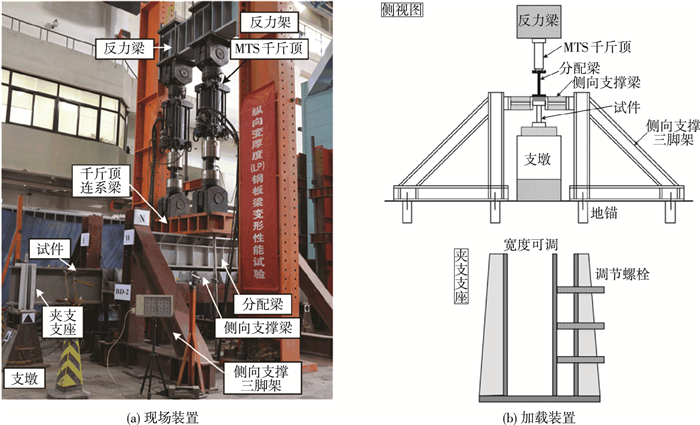
试验在清华大学结构试验室500 t试验机上进行,采用两个150 t MTS千斤顶协同控制加载,见图 2(a).BD-1和BD-2加载时采用分配梁平均分配力于对称两点,并在分配梁与试件上翼缘接触处放置滚轴,以防止摩擦力限制梁的变形.为了避免构件发生侧向整体失稳,采用如图 2(b)所示的侧向支撑装置,约束构件上翼缘的侧向位移.为构件与设备安装方便以及减少摩擦影响,侧向支撑装置与构件之间设置10 mm以内的空隙.由于设备限制,侧向支撑装置长度为3 400 mm,用于约束试件跨中对称部分.支座采用夹支支座,如图 2(b)所示,构件与支座底板接触处设置滚轴,使梁在主平面内可以自由转动,同时限制端部截面扭转变形.
|
图 2 试验加载装置 Figure 2 Diagram of experimental setup |
正式加载前通过施加预估承载力的5%~10%,以消除试验装置之间以及装置与试件之间的空隙,并检查测点和通道.加载过程中采用IMP数据采集系统记录实时荷载、应变以及位移数据,并由计算机直接记录.为研究试验构件的变形性能,本文试件按照GB 50017—201X《钢结构设计规程》(报批稿)建议的S1级塑性截面进行设计,板件宽厚比满足S1级截面要求,即可达全截面塑性,保证塑性铰具有塑性设计要求的转动能力,且在转动过程中承载力不降低.因此,本文在构件出现明显局部屈曲时停止加载,均取停止加载点变形为极限变形,对应荷载为极限荷载.
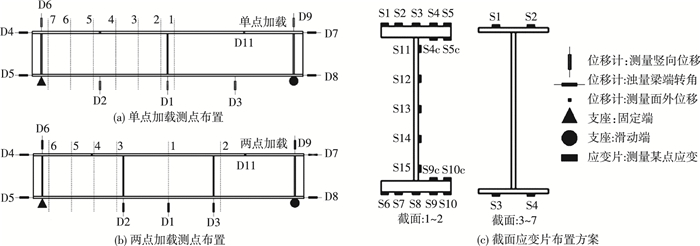
1.5 试验量测方案本次试验主要测量内容包括:1)构件变形性能评价曲线:荷载位移曲线,弯矩转角曲线;2)沿腹板高度方向应变分布;3)沿构件跨度方向上翼缘应变分布.试件荷载通过千斤顶力传感器进行测定,构件测点布置如图 3所示.单点加载构件,布置11个位移计,编号D1~D11,如图 3(a)所示,D1测量构件跨中下翼缘竖向位移,D2和D3测量构件四分之一跨度处下翼缘竖向位移,D4和D7分别测量构件两端上翼缘水平位移,D5和D8分别测量构件两端下翼缘水平位移,D6和D9分别测量两端支座处竖向沉降;此外,由于侧向支撑梁仅可约束梁中部3 400 mm,因此在侧向约束南北两侧10 mm位置设置位移计D10和D11,测量上翼缘侧向约束外侧侧向位移,检验侧向约束的作用;共布置58个应变片,其中,截面1和截面2分别距离跨中150 mm,距加载头外侧50 mm,为局部屈曲最可能发生的截面,截面2~7之间500 mm等距分布,截面7距离支座150 mm,以测定沿翼缘厚度变化方向上应变分布,见图 3(c).两点加载测点布置与单点加载相近,将位移计D2和D3调整得到加载点下方,见图(b);因为纯弯段内力分布相同,仅选择跨中截面布置应变片,共54个应变片.
|
图 3 试件测点布置 Figure 3 Arrangement of testing points |
图 4(a)为全部构件的破坏形态,可以看出4根构件在平面外均有一定程度的扭转,但由于侧向支撑的约束未发生整体失稳.4根构件均发生明显的板件局部屈曲,如图 4所示.BS-1加载点北侧(固定端一侧)上翼缘发生明显屈曲,伴随腹板鼓突,同时下翼缘跨中焊缝出现约10 mm长裂纹,如若继续加载,下翼缘焊缝裂纹将扩展至下翼缘断裂.主要原因是焊缝焊接质量较差,实际运用中,如采用单楔形LP钢板焊接翼缘应采用全熔透等强焊缝并保证焊缝质量,也可直接采用双向变厚度LP钢板.BS-2同样在加载点北侧发生明显局部屈曲,屈曲现象较BS-1更加明显.BD-1在北侧加载点外侧上翼缘和腹板发生局部屈曲,BD-2跨中上翼缘出现局部屈曲现象.

|
图 4 试件破坏形态 Figure 4 Failure modes |
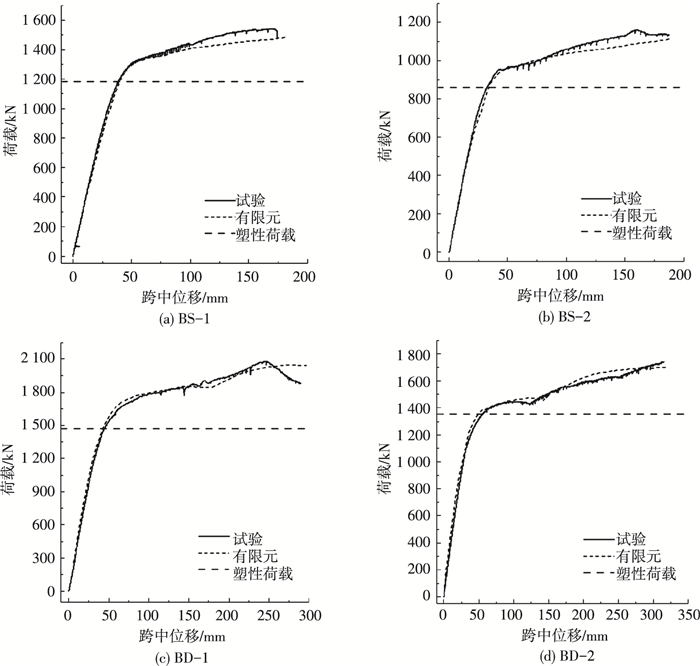
根据构件下翼缘跨中位移计数据和试验加载点总荷载整理得到构件跨中下翼缘竖向位移和总荷载的关系曲线见图 5,水平线代表构件根据实测材性数据计算得到的全截面塑性荷载(全截面屈服荷载).根据构件梁端位移计数据和试验加载点总荷载可以得到弯矩-梁端转角关系曲线,基本形状和规律与图 5相同,篇幅限制不再列出.可以看出,曲线较为平稳且屈服后承载力持续上升,图 5(b)中曲线波动是由于加载设备的不稳定性导致,图 5(c)曲线由于北侧加载点附近板件明显屈曲表现出明显下降段,曲线整体表现出类似于Q345钢材本构曲线相同的强化特性,且试件实际承载力均超过全截面塑性荷载.
|
图 5 构件荷载-位移曲线 Figure 5 Load-displacement curves of specimens |
由于不同构件实测材料力学性能和几何尺寸不同,尤其是变厚度构件刚度与等厚度构件完全不同,为了更好说明构件的荷载-位移关系相对于构件本身性能的关系,将荷载P和位移Δ均转化为无量纲量.其中,标准化荷载=P/Pp,标准化位移=Δ/Δp,Pp为理论计算得到的全截面屈服荷载,Δp为假定刚度与初始刚度相同计算得到的塑性位移,其中翼缘纵向变厚度构件位移采用文献[18-19]中的理论公式进行计算.
汇总4根构件极限承载力及变形性能如表 4所示,其中Pu、Δu分别为极限荷载与对应极限位移,
| 表 4 构件极限荷载及变形能力 Table 4 The ultimate load and deformation capacity |
延性在结构抗震设计中是一个非常重要的指标,通常使用延性系数来表示,本文采用位移延性系数RΔ=Δu/Δp作为构件延性的宏观表达.由表 4可以看出,所有构件跨中竖向位移均达到了塑性位移,且位移延性系数RΔ均达到5倍以上.试验终止时刻变厚度构件延性相对较差,单点加载和两点加载情况下,相比等厚度构件位移延性系数RΔ降低22.47%和26.63%.
由于加载装置限制,单点加载构件最终跨中位移为200 mm左右,两点加载构件最终跨中位移为300 mm左右,除BD-1外其余构件承载力未出现明显下降段,说明构件实际具有更大变形能力.综上,可以认为试验构件变形能力已达到密实截面的要求.
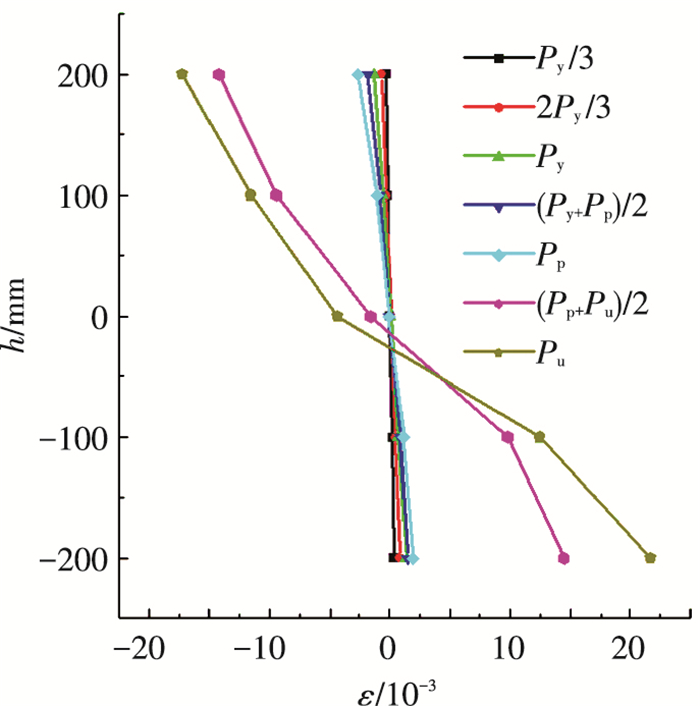
2.3 荷载-应变曲线 2.3.1 沿截面高度腹板应变分布根据构件腹板应变片数据和荷载数据整理得到构件在荷载分别为Py/3、2Py/3、Py、(Py+Pp)/2、Pp、(Pp+Pu)/2、Pu时的应变分布(Py、Pp、Pu分别为屈服荷载、塑性荷载和极限荷载),选取每个构件屈曲明显腹板应变随截面高度分布如图 6所示,其中,横坐标为应变片所测应变;纵坐标为应变片测点到横截面强轴的距离,单位为mm.
|
图 6 沿截面高度腹板应变分布(BS-2) Figure 6 Web strain distribution along the sectionheight (BS-2) |
可以看出构件腹板应变分布随加载过程的变化,屈服荷载前完全为直线,满足平截面假定,达到塑性荷载时直线开始出现弯折,达到极限荷载之前和达到极限荷载时,已不满足平截面假定.
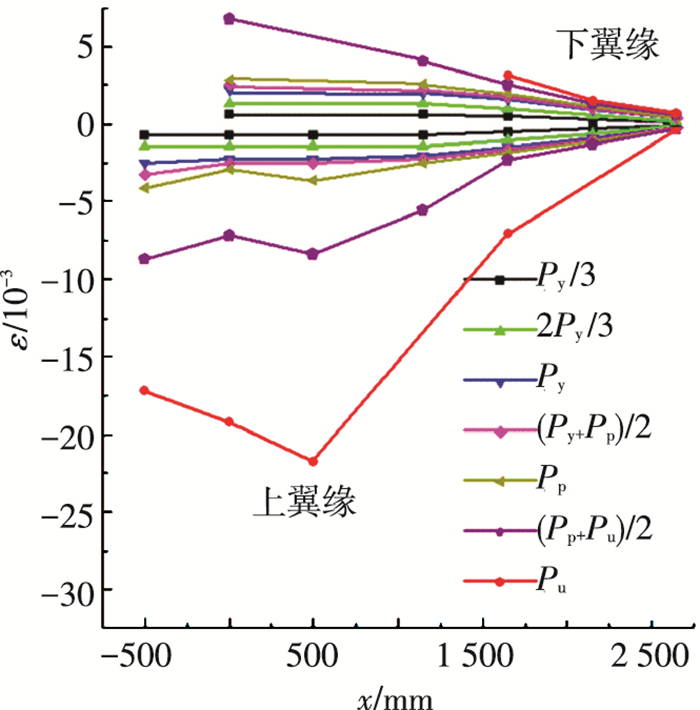
2.3.2 沿梁跨度方向翼缘应变分布根据沿梁跨度方向布置的应变片,同样可以整理得到构件在荷载分别为Py/3、2Py/3、Py、(Py+Pp)/2、Pp、(Pp+Pu)/2、Pu时的应变分布,见图 7.其中,横坐标为应变片测点到跨中的距离,单位为mm;纵坐标为应变片所测应变.
|
图 7 沿梁跨度方向翼缘应变分布(BD-1) Figure 7 Flange strain distribution along beam span (BD-1) |
可以看出,沿梁跨度方向翼缘应变随荷载增加的变化过程,当荷载小于屈服荷载之前,应变基本上呈线性分布,随着荷载增加,应变分布脱离线性,单点加载跨中部分和两点加载纯弯段部分,应变极大,形成了明显塑性铰,且发生局部屈曲板件处应变较大.除此之外,由于上翼缘受压导致局部屈曲的存在,使得上下翼缘应变分布并不完全对称.
2.4 无约束段面外位移由侧向支撑外侧布置的位移计测量数据可以看出,由于试件与侧向支撑之间的间隙,使得构件无约束部分在加载过程中并非没有加载面外的位移,且随加载过程不断变化,但是变化范围很小,基本上在±10 mm范围内,与侧向支撑与构件之间所留间隙范围相同,说明侧向支撑对全构件起到了约束作用,有效防止了整体失稳的发生.
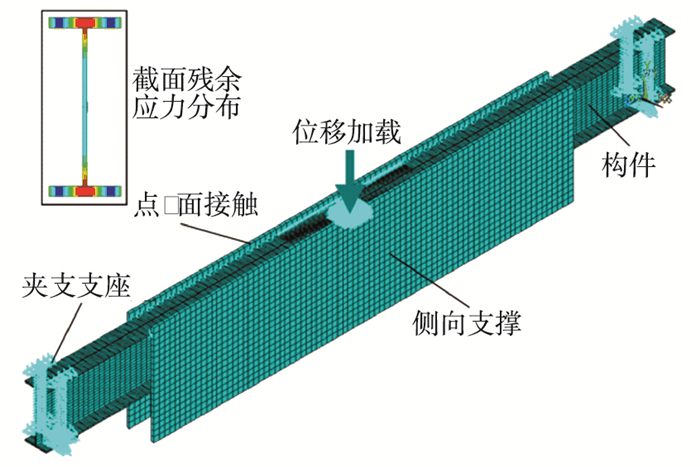
3 有限元验证 3.1 有限元模型本文采用通用有限元软件ANSYS对4根试验构件进行数值模拟,模型模拟构件、夹支支座、垫板以及侧向支撑梁,通过点-面接触单元模拟构件上翼缘与侧向支撑板之间的摩擦关系,均采用SOLID185实体单元,并采用位移加载,加密跨中网格,见图 8.
|
图 8 有限元模型 Figure 8 The finite element model |
由于LP钢板强度沿纵向变化,将翼缘划分为长度为200 mm的小段,分别输入基于实际数据线性插值得到各段材性数据.采用一阶特征值屈曲模态对理想模型节点坐标进行更新,变化幅值为实测初始缺陷值.残余应力模型采用文献[20]中的统一分布模型,截面残余应力分布见图 8.
3.2 与试验结果对比分析有限元计算得到的荷载-位移关系曲线见图 5,对比承载力结果如表 5所示,其中Ftest为试验极限承载力,FFEA为有限元计算得到的试验极限位移Δu对应承载力.
| 表 5 试验值与有限元分析结果对比 Table 5 Comparison between test and FEA results |
可以看出,在达到理论塑性荷载前及超过塑性荷载一定范围时,有限元试验结果与试验结果基本一致,但是由于试验中构件变形较大时会发生侧向支撑允许范围内的扭转,并与侧向支撑接触,在构件继续向下变形的过程中产生摩擦,而且摩擦力随着荷载的增大而增大,且对接触面积十分敏感,因此,曲线强化段模拟略差,但相对误差不超过5 %.建议在进一步参数化分析中,采用理想侧向约束边界条件.
4 结论本文对2根翼缘纵向变厚度工型截面梁和2根等厚度工型截面梁进行了静力加载试验,研究了单点加载和两点加载情况下翼缘纵向变厚度工型截面简支梁的变形性能,与等厚度梁进行了对比,并采用ANSYS进行了数值模拟,获得以下结论:
1) 在有效侧向支撑约束条件下,按照GB 50017—201X《钢结构设计规范》中S1级塑性截面设计的翼缘纵向变厚度工型截面简支梁与等厚度工型截面梁一样,且均在极大变形情况下,发生局部屈曲.
2) 4根构件均达到了全截面屈服荷载Pp,且全截面屈服后进入强化阶段.由于材料强度提高使得翼缘纵向变厚度梁不仅可以在保证承载力的情况下大大减少用钢量,而且可以获得更大的强度储备;在材料强度和最大受力截面相同的情况下,可保证构件承载力不降低.
3) 4根构件跨中竖向位移均达到了塑性位移,且位移延性系数RΔ均达到5倍以上.虽然试验终止时刻翼缘纵向变厚度构件的延性与等厚度梁相比较差,但是也可以达到密实截面的变形要求,满足塑性设计要求.
4) 考虑侧向支撑摩擦的有限元模型与试验曲线吻合良好,但建议在进一步参数分析中使用理想侧向约束.
| [1] |
沈祖炎, 温东辉, 李元齐. 中国建筑钢结构技术发展现状及展望[J].
建筑结构, 2009, 39(9): 15-25.
SHEN Zuyan, WEN Donghui, LI Yuanqi. State-of-the-art: Technical progress of steel building structures in China[J]. Building Structure, 2009, 39(9): 15-25. |
| [2] |
姚文聪. 梭形变截面工字形简支钢梁的整体稳定分析[D]. 长沙: 湖南大学, 2010.
YAO Wencong. Overall stability analysis of tapered simply-supported I-beams[D]. Changsha: Hunan University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10532-2010238159.htm |
| [3] |
刘晓玲, 王元清, 王玉银, 等. 纵向变厚度(LP)钢板的工程应用和研究进展[J].
工业建筑, 2015, 45(S): 1027-1035.
LIU Xiaoling, WANG Yuanqing, WANG Yuyin, et al. Review of structural application and research of longitudinally profiled steel plate (LP steel plate)[J]. Industrial building, 2015, 45(S): 1027-1035. |
| [4] |
OKANO S. High performance steels for bridge construction and examples of their application[J].
Welding International, 2008, 22(11): 746-754.
DOI: 10.1080/09507110802550224 |
| [5] |
王元清, 刘晓玲, 刘明, 等. 纵向变厚度钢板力学性能试验研究[J].
钢结构, 2017, 32(4): 16-21.
WANG Yuanqing, LIU Xiaoling, LIU Ming, et al. Experimental research of mechanical properties of longitudinally profiled steel plate[J]. Steel Structure, 2017, 32(4): 16-21. |
| [6] |
RICHTER K, SCHMACKPFEFFER H. Longitudinally profiled plates cut costs[J].
Joining & Materials, 2008, 11: 270-273.
|
| [7] |
MURAKAMI S, NOBUO N. Ultimate strength evaluation of tapered plate in compression[C]//Proc. 5th International Colloquium on Stability and Ductility of Steel Structures. Nagoya:[s.n.], 1997: 133-140.
|
| [8] |
村上茂之, 西村宣男, 崛田毅. 自由突出テーパープレートの圧縮強度[J].
構造工学論文集, 1997, 34: 107-116.
MURAKAMI S, NISHIMURA N, HOTTA T. Ultimate strength of outstanding tapered plates incompression[J]. Journal of Structural Engineering, 1997, 34: 107-116. |
| [9] |
村山峻一朗, 大谷礼央, 永藤壽宮. LP鋼板における力学的挙動特性について: 中部支部研究発表会I-031[R]. [S. l. ]: 日本土木学会, 2009.
|
| [10] |
松野健太, 永藤壽宮. 初期不整を有する LP鋼板のI形断面における挙動特性: 中部支部研究発表会I-019[R]. [S. l. ]: 日本土木学会, 2012.
|
| [11] |
井川大裕, 坂井悠佑, 吹田啓一郎, 等. 変厚鋼板の材料特性と柱梁接合部試験体について: 変厚鋼板を梁フランジに用いた増厚梁端接合部の塑性変形能力その1: 学術講演梗概集22527[R]. 関東: 日本建築学会, 2011.
IKAWA D, SAKAI Y, SUITA K, et al. Plastic deformation capacity ofmoment frame connection with the thickness of beam flanges increased near the connection region Part 1-Mechanical properties of steel plate with variable thickness: Collection of Academic Dissertation 22527[R]. Kanto: Architectural Institute of Japan, 2011. |
| [12] |
井川大裕, 坂井悠佑, 吹田啓一郎, 等. 柱梁接合部の載荷実験: 変厚鋼板を梁フランジに用いた増厚梁端接合部の塑性変形能力その 2: 学術講演梗概集22527[R]. 関東: 日本建築学会, 2011.
IKAWA D, SAKAI Y, SUITA K, et al. Plastic deformation capacity ofmoment frame connection with the thickness of beam flanges increased near the connection region Part 2-Loading test of beam to column connection: Collection of Academic Dissertation 22528[R]. Kanto: Architectural Institute of Japan, 2011. |
| [13] |
AOKI T, TAKAKU T, FUKUMOTO Y, et al. Experimental investigation for seismic performance of framed structures having longitudinally profiled plates[J].
Journal of Constructional Steel Research, 2008, 64(7): 875-881.
|
| [14] |
FUKUMOTO Y, UENOYA M, NAKAMURA M, et al. Cyclic performance of stiffened square box columns with thickness tapered plates[J].
Journal of Steel and Structures, 2003, 3(2): 107-15.
|
| [15] |
王星堯. LP鋼板柱耐震行為之研究[D]. 台北: 國立台灣科技大學, 2013.
WANG Xingyao. Steel bridge columns with longitudinally profiled steel plate for seismic resistance[D]. Taipei: National Taiwan University of Science and Technology, 2013. |
| [16] |
施刚, 班慧勇, 石永久, 等. 结构构件整体几何初始缺陷测量方法: CN102288081A[P]. 2011-12-21.
SHI Gang, BAN Huiyong, SHI yongjiu, et al.Overall geometric imperfection measuring method of structure members: CN102288081A[P]. 2011-12-21. |
| [17] |
王元清, 袁焕鑫, 石永久. 一种连续量测结构构件局部几何初始缺陷的装置: CN103063172A[P]. 2013-04-24.
WANG Yuanqing, YUAN huanxin, SHI yongjiu. A device for local geometric imperfection measurement of structure members: CN103063172A[P]. 2013-04-24. |
| [18] |
王元清, 刘晓玲, 王玉银, 等. 单点加载翼缘纵向变厚度工型截面简支梁变形解析解法[J].
沈阳建筑大学学报(自然科学版), 2016, 32(4): 577-583.
WANG Yuanqing, LIU Xiaoling, WANG Yuyin, et al. Theoretical deformation solution of I-section beam with longitudinally variable thickness flanges under single point loading[J]. Journal of Shenyang Jianzhu University (Natural Science), 2016, 32(4): 577-583. DOI: 10.11717/j.issn:2095-1922.2016.04.01 |
| [19] |
王元清, 刘晓玲, 王玉银, 等. 两点加载翼缘纵向变厚度工型截面简支梁变形的解析解法[J].
应用力学学报, 2016, 33(6): 976-981.
WANG Yuanqing, LIU Xiaoling, WANG Yuyin, et al. Theoretical deformation solution of I-section beam with longitudinally variable thickness flanges under two point loading[J]. Chinese Journal of Applied Mechanics, 2016, 33(6): 976-981. |
| [20] |
班慧勇, 施刚, 石永久. 高强钢焊接构件工字形横截面残余应力试验及同一分部模型研究[J].
工程力学, 2014, 31(8): 83-91.
BAN Huiyong, SHI Gang, SHI Yongjiu. Experimental and unified model investigations on residual stress within high strength steel welded I-sections[J]. Engineering Mechanics, 2014, 31(8): 83-91. |
 2017, Vol. 49
2017, Vol. 49


