2. 土木工程智能防灾减灾工信部重点实验室(哈尔滨工业大学),哈尔滨 150090
2. Key Laboratory of Smart Prevention and Mitigation of Civil Engineering Disasters(Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China
作为楼盖结构的平板网架多应用于会议厅、室内运动场等建筑中,承担较大荷载,且跨度较大.如果在地震中发生破坏甚至倒塌,其上部非结构构件也将严重破坏,经济损失巨大,修复费用高.因此保障网架结构楼盖的地震安全、减轻结构的预期损伤具有重要意义.
网架结构地震易损性的研究除了能够评估结构的抗震性能,为基于性能的抗震设计和结构风险评估奠定基础外,还可以为网架结构灾后维修及加固的决策方案提供建议[1].
国内外学者对于网架结构的抗震设计理论已经开展了系列基础研究,包括计算方法的讨论[2]、线弹性分析及考虑材料非线性的响应等[3],一些研究者还结合较为精细的模型研究了网架结构的强震连续倒塌机理[4].而结构的地震易损性研究最早开始于核电领域[5],随后,在建筑结构[6]和桥梁工程[7]中逐步发展应用,且已经有学者应用该理论研究了单层网壳结构的地震易损性[8],这也为本文的研究方法提供了重要参考.
本文选取应用广泛的正放四角锥平板网架楼盖(orthogonal pyramid space grid, OPSG)结构,首先基于ANSYS软件分析了结构的强震全过程响应,考察了网架结构的破坏模式,提出了适用于正放四角锥平板网架结构的地震损伤程度指标和灾害等级划分标准.然后讨论了结构参数的敏感性和地震波对结构响应的影响,进而开展基于结构-地震动样本的地震易损性研究.
1 正放四角锥平板网架的强震响应 1.1 有限元建模本文网架结构的支承形式为周边三向铰接,网架平面为正方形,边长(跨度L)分别取48 m、72 m及96 m.网架结构杆件设计满足常规设计要求,网架取均布恒荷载5.0 kN/m2和活荷载2.5 kN/m2,抗震设防烈度为8度.本文不考虑混凝土楼板与网架的耦合作用,仅考虑混凝土楼板质量的影响.钢材采用Q235B级钢材,网架结构的所有杆件均按照满应力的设计原则确定截面,且结构刚度满足《空间网格结构技术规程》的要求;杆件设计中控制应力为215 MPa,控制位移为L/250.从静力分析结果来看,结构的强度和刚度均充分利用,其中72 m跨度的网架结构已达到设计限值.
除特殊说明外,将网架结构用以下代号表示:
WJ48_33_24_5025:48—跨度48m;33—网格尺寸3 m×3 m;24—网架高度2.4 m;5025—楼面静载5.0 kN/m2,活载2.5 kN/m2.模型WJ72_45_36_5025和WJ96_66_48_5025同理.
分析中钢材本构采用双线性随动强化模型,重力荷载代表值取为1.0恒载+0.5活载,采用集中质量法将均布荷载等效成质量单元施加在节点上.根据以上原则建立基于ANSYS的动力有限元模型,如图 1所示.

|
图 1 正放四角锥平板网架结构有限元模型 Figure 1 Finite element model of OPSG |
参照文献[9]对网壳结构强震响应的研究,采用基于多重响应的全荷载域动力时程分析方法.考察的结构响应取结构最大节点位移、结构屈服杆件比例及结构最大塑性应变.
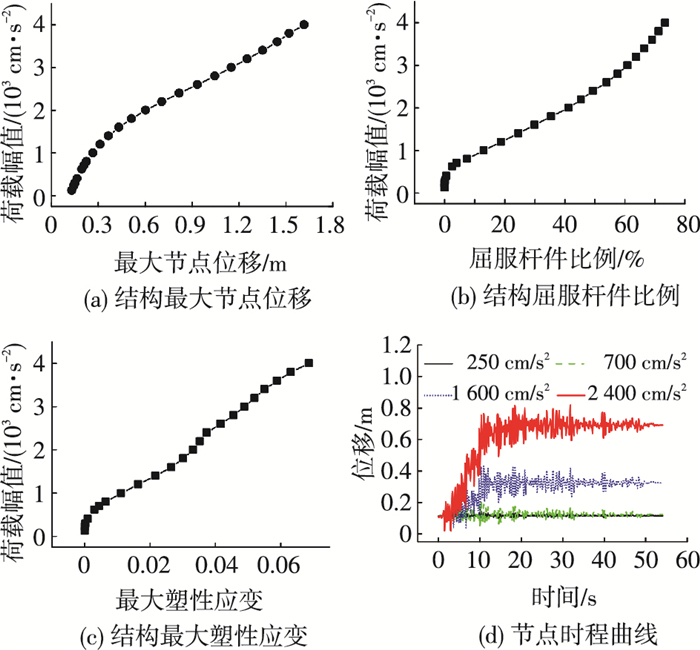
本节仅以WJ48_33 _24_5025模型受三向TAFT地震作用为例,通过ANSYS有限元计算获得了各结构响应的全荷载域曲线,并将其列于图 2中.
|
图 2 网架WJ48_33_24_5025在三向TAFT地震作用下响应曲线 Figure 2 Response curves of WJ48_33_24_5025 under TAFT in three directions |
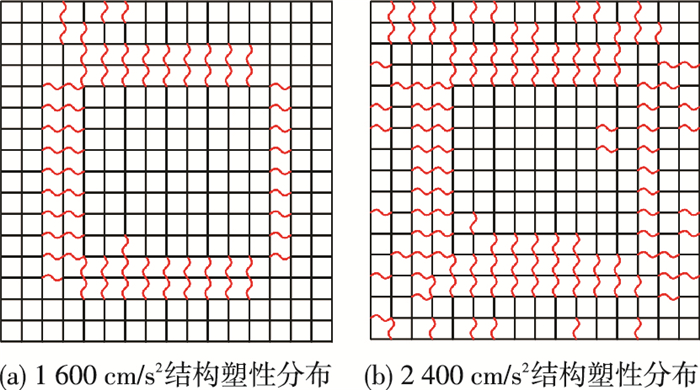
从图 2(a)~(c)中可以看到地震荷载幅值在250 cm/s2前,结构一直处于弹性状态,结构中没有进入塑性的杆件;荷载幅值处于250 cm/s2~700 cm/s2时,结构的塑性发展仍然很浅,位移曲线也基本保持线性变化,结构的整体刚度基本不变;随地震强度继续增大,结构塑性发展逐渐加深,可以看到位移曲线斜率减小很快,即结构的整体刚度在迅速降低;荷载幅值为1 600 cm/s2时,节点最大位移达到0.43 m,屈服杆件比例为30%(屈服杆件分布见图 3(a)),再观察图 2(d)中节点位移时程曲线,节点振动平衡位置发生较大偏移.当荷载幅值达到2 400 cm/s2时,结构刚度严重弱化,结构位移达到0.82 m(约为跨度的1/58),屈服杆件比例也已经超过50%(见图 3(b)),尽管结构没有塌陷,但是如此大的位移已能使楼面板及附属结构严重破坏,此时结构的变形呈倒锥形(见图 4).
|
注:图中弯曲线表示塑性发展程度较深的杆件,由于上弦层、腹杆层和下弦层分布基本一致,仅以上弦层为例. 图 3 网架WJ48_33_24_5025在三向TAFT地震作用下结构塑性分布 Figure 3 Plasticity distribution of WJ48_33_24_5025 under TAFT in three directions |

|
图 4 荷载幅值2 400 cm/s2时的最大变形图(放大5倍) Figure 4 The maximum deformation map under 2 400 cm/s2 |
据以上分析发现,由于平板网架是受弯结构体系,结构的破坏属于整体强度破坏,不存在局部结构失稳破坏现象;结构破坏前塑性发展较为深入,有明显的变形作为预兆,属于延性破坏.
2 参数敏感性分析参数敏感性分析是从定量的角度研究有关参数发生变化时对某个关键指标的影响程度.方法可分为局部敏感性分析和全局敏感性分析[10],其中前者关注的是局部参数变化对输出结果的影响,而后者的重心是在所有参数共同随机变化的情况下观察某一个输出结果的变化趋势.本文利用局部敏感性方法对网架结构各参数开展敏感性分析,为后续地震易损性分析中的Monte-Carlo抽样提供依据.
2.1 结构随机参数及其概率分布模型在实际工程中,网架材料或构件的加工误差、施工误差等都是随机量,随机误差导致结构参数的不确定性.本节选取以下5个参数作为考察对象,各参数的概率分布模型、变异系数等信息见表 1.每个参数在其主要分布区间内(即5%~95%分位值,参数变化范围)均匀选取计算值.
| 表 1 结构参数概率分布模型 Table 1 Distribution model of structure parameters |
选取TAFT地震记录三向输入,分别计算220、1 000和1 600 cm/s2三种幅值下的结构响应.比较分析结构响应对各参数的敏感性.
分析发现各响应的敏感性规律基本一致,以下分析均以结构最大节点位移变化曲线为例.
1) 钢材屈服强度:
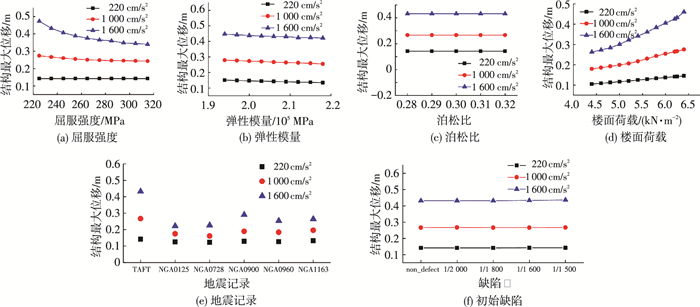
如图 5(a)所示,当荷载幅值为220 cm/s2时,结构响应保持不变,这是因为结构处于弹性阶段;当荷载幅值处于1 000 cm/s2和1 600 cm/s2时,结构响应随着屈服强度的增加有明显减小趋势.因此,钢材屈服强度对结构响应的影响不可忽略,在后续分析中应将其视作随机性因素处理.
|
图 5 结构响应随各参数的变化 Figure 5 Structure response changes as parameters change |
2) 钢材弹性模量:
如图 5(b)所示,在三种荷载幅值作用下各响应参数几乎没有变化,即结构响应对弹性模量的敏感性小,后续分析可将其视为确定性因素.
3) 泊松比:
如图 5(c)所示,结构响应随泊松比变化保持不变,即不具有敏感性,应将其视为确定性因素.
4) 楼面荷载(1.0恒荷载+0.5活荷载):
如图 5(d)所示,随着楼面荷载的逐渐增加,结构响应也明显增大,即敏感性显著,应作为随机性因素处理.
2.3 地震动和初始几何缺陷的敏感性分析本节选取6条地震记录,地震动的影响如图 5(e)所示.在小荷载幅值作用下影响程度不显著,而在大幅值作用下结构响应的变化程度较大,不可忽略.因此后续分析中应将其视为随机性因素.
实际工程中的网架存在缺陷,本文选取了L/1 500、L/1 600、L/1 800和L/2 000四种结构初始缺陷(缺陷为特征值屈曲缺陷)进行计算.结果见图 5(f),可以看出在各种荷载幅值作用下,结构响应随缺陷的增加没有变化,即网架是一种缺陷不敏感体系.分析原因如下:正放四角锥平板网架是受弯结构体系,受力机理同混凝土双向楼板,结构沿径向不受轴力作用,初始几何缺陷不会引起较明显的二阶效应.因此,后续分析中将初始几何缺陷视为确定性因素并统一设定为L/1 500.
3 地震易损性分析 3.1 结构损伤程度指标GB/T 24335—2009《建(构)筑物地震破坏等级划分》[13]对结构在地震作用下的破坏状态作了详细的划分,这些破坏状态的定义与目前国外对于结构破坏状态的定义基本相同[14].参考这些标准,并根据本文第1节中正放四角锥平板网架在强震作用下的响应特征,提出了适用于正放四角锥平板网架的损伤等级划分(表 2).根据网架结构杆件的塑性发展程度和刚度削弱程度给出了相应的判别界限.
| 表 2 正放四角锥平板网架结构地震损伤等级划分 Table 2 Damage grades of orthogonal pyramid space grid under earthquakes |
为了定量表示结构的损伤状态,很多学者开展了相关研究.例如文献[15]研究了仅考虑结构变形的单参数损伤模型,文献[16]提出了非线性组合形式的双参数地震损伤模型,文献[17]提出以结构平均塑性应变,结构最大节点位移和结构塑性发展程度等多种结构响应指标综合获得的损伤因子DS来定义结构的损伤程度等.本文根据网架结构的特殊情况,选择仅考虑位移的单参数损伤模型.这是因为节点最大位移、结构屈服杆件比例和结构最大塑性应变等指标的发展趋势相同且相互协调.
参考文献[17],定义结构损伤因子DS表示网架的损伤程度(如式(1)所示),其中当DS=0时表示结构完好,当DS=1时表示结构破坏失效.
| $ {{D}_{\rm{S}}}=\frac{{{d}_{\rm{m}}}-{{d}_{\rm{e}}}}{L/100}. $ | (1) |
式中:DS为结构损伤因子;L为网架跨度;dm为结构最大节点位移;de为材料出现塑性屈服时刻的结构最大节点位移,即弹性极限位移.
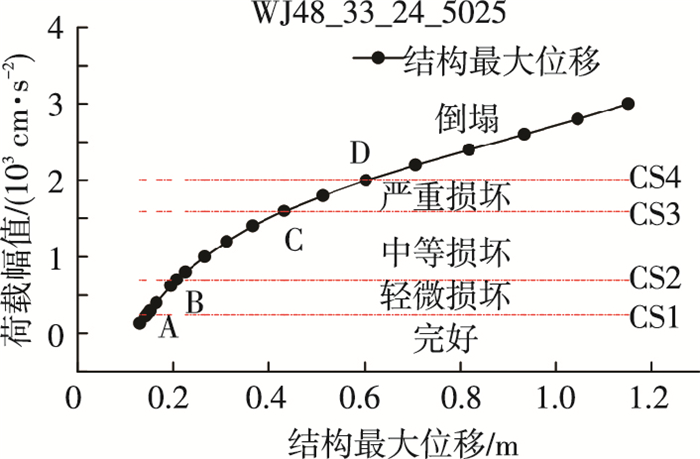
根据表 2的划分原则,以WJ48_33_24_5025网架结构在TAFT三维地震作用下结构最大节点位移曲线为例,在图 6中标出了各损伤等级对应的响应范围及4个临界状态(CS1、CS2、CS3以及CS4),并计算得出各临界状态对应的损伤因子,如表 3所示.
|
图 6 网架地震损伤等级划分示意 Figure 6 Sketch of damage grades |
| 表 3 WJ48_33_24_5025各临界状态下的结构响应及损伤因子 Table 3 Structural responses and damage factors of WJ48_33_24_5025 at each critical state |
将3个结构的损伤因子统一列于表 4中,最终给出各界限的建议取值和各损伤等级的建议取值范围.因此正放四角锥平板网架结构各个损伤等级对应的损伤因子建议取值范围见表 5.
| 表 4 损伤因子建议取值 Table 4 Suggested values of damage factors |
| 表 5 损伤等级对应的损伤因子建议取值范围 Table 5 Suggested damage factor ranges of damage grades |
结构地震易损性是指结构在某一给定危险性水平的地震作用下地震需求Sd达到或超过结构抗力Sc的条件概率(如式(2)所示),与结构形式、施工质量和结构所在场地有关,是结构的本身属性.
| $ {{P}_{\rm{f}}}=P\left[\frac{{{S}_{\rm{d}}}}{{{S}_{\rm{c}}}}\ge 1 \right], $ | (2) |
式中Pf是某一给定状态下的失效概率.
地震需求和结构抗力均服从对数正态分布[18],即可将失效概率表示为
| $ {{P}_{\rm{f}}}=P\left[\frac{{{S}_{\rm{d}}}}{{{S}_{\rm{c}}}}\ge 1 \right]=1-\mathit{\Phi }\left( \frac{{\rm{ln}}\left( 1 \right)-\lambda }{\zeta } \right)~=\mathit{\Phi }\left(\frac{\lambda }{\zeta }\right), $ | (3) |
式中λ表示ln(Sd/Sc)的平均值,ζ表示ln(Sd/Sc)的标准值.
网架结构地震易损性分析的基本步骤如下:
1) 选择网架结构模型并抽样生成一定数量的结构样本,同时选择一定数量的地震记录.
2) 组成一定数量的结构-地震动样本.
3) 通过有限元软件计算得出每个样本的结构响应.
4) 以地震峰值加速度为自变量,对得到的结构响应数据进行回归分析.
5) 由回归分析结果得到结构响应与地震幅值之间的概率关系式,并绘制易损性曲线.
3.3 地震易损性算例分析仍以WJ48_33_24_5025结构为例:
根据参数敏感性分析,将泊松比、弹性模量和初始几何缺陷作为确定性因素并择其标准值参与计算,屈服强度和楼面荷载作为随机因素参与Monte-Carlo抽样产生计算样本,同时随机选取20条地震记录,所选择地震动属于远场地震动,震级大,断层距小,场地类别为Ⅱ类场地.最终形成结构-地震动样本20组.
利用ANSYS程序对每组样本进行增量动力分析,并从每组样本的计算结果中均匀选取10个结果数据.其中数据包括结构最大位移dm和结构弹性极限位移de,并计算出对应的dm/de和DS.
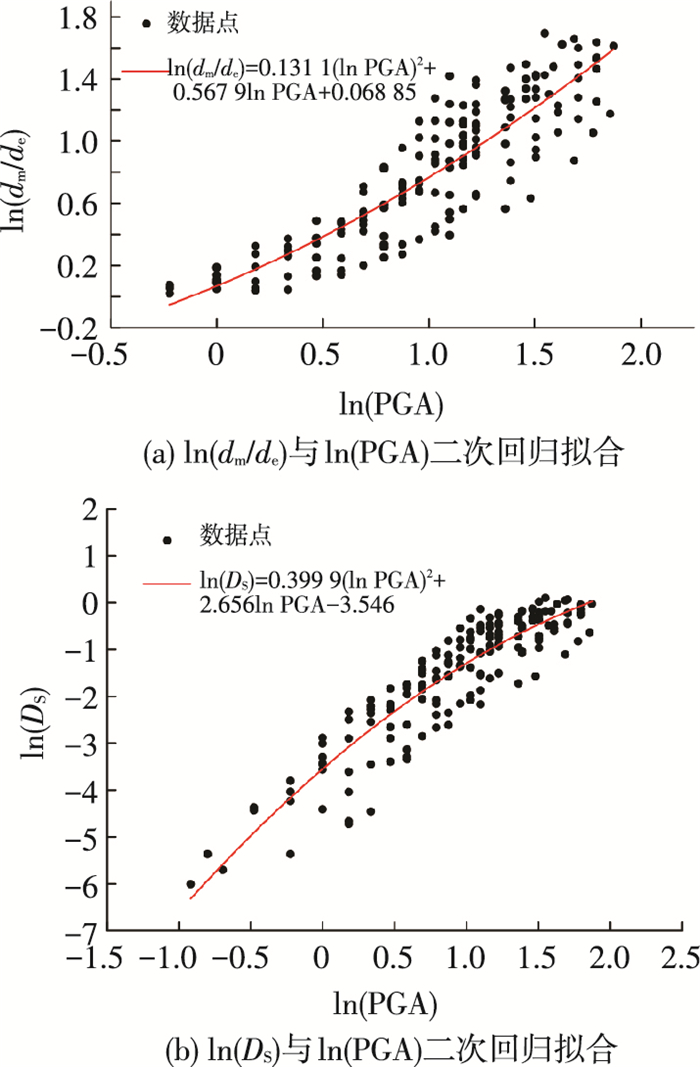
对上述数据进行二次回归处理,得到如图 7所示的结构响应与地震峰值加速度之间的关系曲线.
|
图 7 网架WJ48_33_24_5025结果回归处理 Figure 7 Quadratic regression for the results of WJ48_33_24_5025 |
从而得到正放四角锥平板网架结构地震易损性曲线的表达式:
| $ {{P}_{\rm{f}}}\left( 0 \right)=\mathit{\Phi }\left[\frac{{{\lambda }_{0}}}{{{\zeta }_{0}}} \right]~=\mathit{\Phi }\left[\frac{0.113\ 1{{\left( \ln \ \rm{PGA} \right)}^{2}}+0.567\ 9\ln \ \rm{PGA}+0.068\ 85}{0.216\ 1} \right]. $ | (4) |
| $ {{P}_{\rm{f}}}\left( 0.1 \right)=\mathit{\Phi }\left[\frac{{{\lambda }_{0.1}}}{{{\zeta }_{0.1}}} \right]~=\mathit{\Phi }\left[\frac{-0.399\ 9{{\left( \ln \ \rm{PGA} \right)}^{2}}+2.656\ln \ \rm{PGA}-3.546-\ln \left( 0.1 \right)}{0.539\ 1} \right]. $ | (5) |
| $ {{P}_{\rm{f}}}\left( 0.5 \right)=\mathit{\Phi }\left[\frac{{{\lambda }_{0.5}}}{{{\zeta }_{0.5}}} \right]~=\mathit{\Phi }\left[\frac{-0.399\ 9{{\left( \ln \ \rm{PGA} \right)}^{2}}+2.656\ln \ \rm{PGA}-3.546-\ln \left( 0.5 \right)}{0.539\ 1} \right]. $ | (6) |
| $ {{P}_{\rm{f}}}\left( 1.0 \right)=\mathit{\Phi }\left[\frac{{{\lambda }_{1.0}}}{{{\zeta }_{1.0}}} \right]~=\mathit{\Phi }\left[\frac{-0.399\ 9{{\left( \ln \ \rm{PGA} \right)}^{2}}+2.656\ln \ \rm{PGA}-3.546}{0.539\ 1} \right]. $ | (7) |
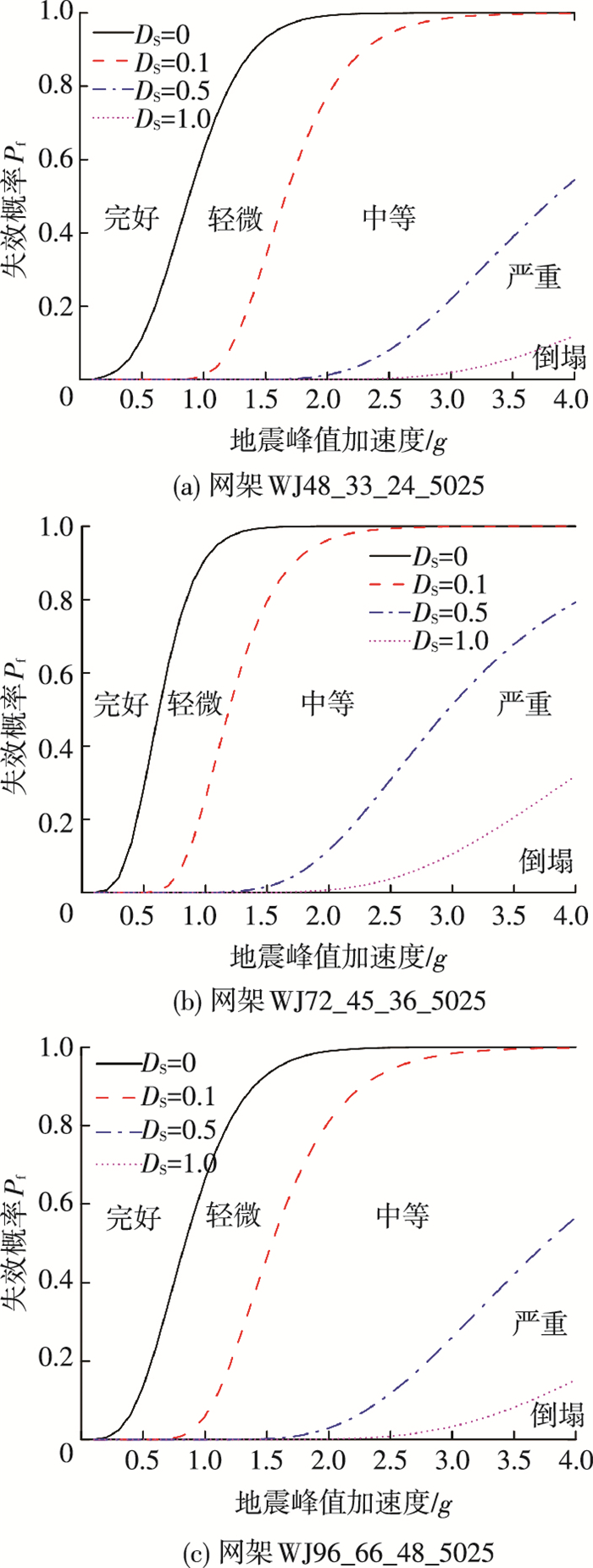
根据式(4)~(7)可以绘制出WJ48_33_24_5025网架结构的地震易损性曲线见图 8(a).根据曲线可以看到,结构在峰值加速度为0.40g(8度罕遇)时保证完好的概率仍有95%,而且即使出现0.62g(9度罕遇)强烈地震时,结构保证完好的概率仍能达到79%.据此可以得出WJ48_33_24_5025网架结构抗震性能良好的结论.
|
图 8 地震易损性曲线 Figure 8 Seismic fragility curves |
同理,对于72 m跨度和96 m跨度的网架结构,分析方法和步骤一致,对应的地震易损性曲线如图 8(b)和8(c)所示.根据易损性曲线可知,与48 m跨度的网架结构相类似,这两个结构的抗震性能也都很好.
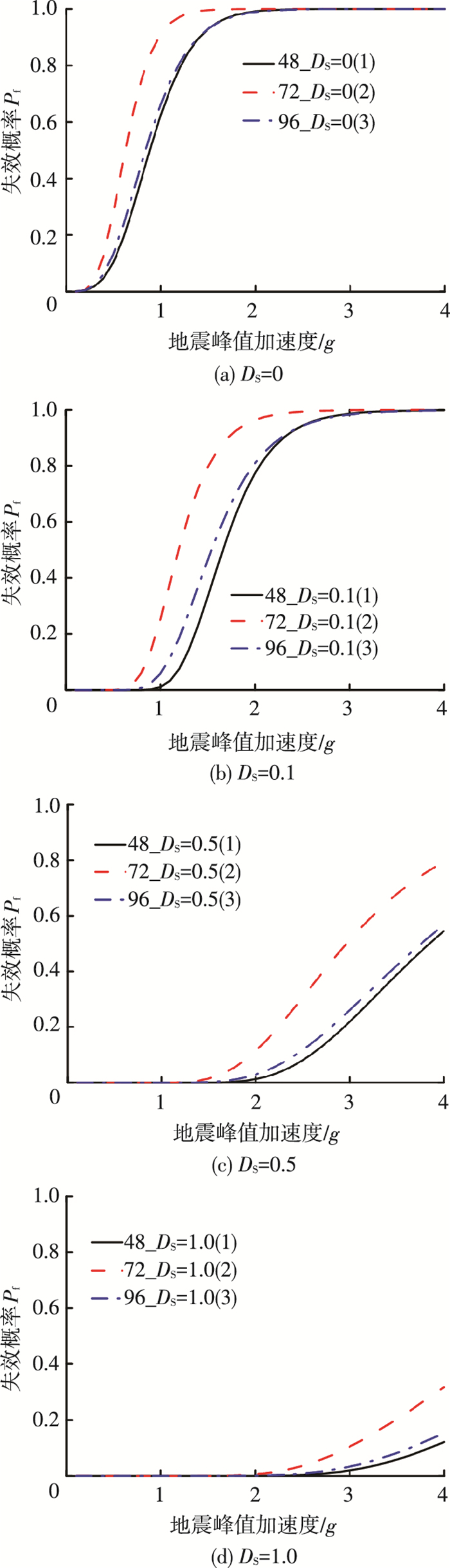
将3个结构的地震易损性曲线进行对比(图 9).从图中可以发现:4种破坏状态下结构(1)、(3)的曲线比较接近,结构(2)曲线均处于(1)、(3)的上方,即72 m跨度网架结构的失效概率略高于其他两种跨度结构.原因是进行网架结构静力设计时,72 m跨度网架结构已达到设计限值,因此结构的地震易损性应与截面选择有很大关系.从图中还可以看出,结构失效概率没有随网架跨度的增加而增大,所以结构的地震易损性基本与网架跨度无关.
|
图 9 易损性曲线比较 Figure 9 Comparison of seismic fragility curves |
1) 根据结构全荷载域时程分析发现,由于平板网架是受弯结构体系,其破坏属于整体强度破坏,且有明显的预兆,是典型的延性破坏.
2)参数敏感性分析表明网架结构响应对屈服强度、楼面荷载及地震记录较敏感,而对弹性模量、泊松比及初始几何缺陷等因素不敏感.
3) 提出了适用于网架结构的损伤等级划分标准及性能水准,建立了基于位移的结构损伤模型和损伤程度指标.
4) 开展了结构地震易损性研究,发现网架结构具有良好的抗震性能,且结构地震易损性基本与跨度无关、与杆件截面选择有较大关系.
| [1] |
吕大刚, 李骁鹏, 王光远. 基于可靠度和性能的结构整体地震易损性分析[J].
自然灾害学报, 2006(2): 107-114.
LV Dagang, LI Xiaopeng, WANG Guangyuan. Global seismic fragility analysis of structures based on reliability and performance[J]. Journal of Natural Disasters, 2006(2): 107-114. |
| [2] |
崔振亚. 网架结构设计中的几个问题[J].
力学学报, 1974(4): 163-167.
CUI Zhenya. Several problems in the design of grid structure[J]. Chinese Journal of Theoretical and Applied Mechanics, 1974(4): 163-167. |
| [3] |
王策, 沈世钊. 网架结构非线性动力反应及倒塌分析[J].
哈尔滨建筑工程学院学报, 1993, 26(6): 38-43.
WANG Ce, SHEN Shizhao. Nonlinear dynamic response and collapse analysis of grid structures[J]. Journal of Harbin University of Civil Engineering, 1993, 26(6): 38-43. |
| [4] |
张卫中. 网架结构在强震作用下的倒塌破坏机理研究[D]. 北京: 北京工业大学, 2012.
ZHANG Weizhong. The collapse mechanism study of grid structures subjected to strong-earthquake[D]. Beijing: Beijing University of Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10005-1012036897.htm |
| [5] |
GHIOCEL D M, WILSON P R, THOMAS G G, et al. Seismic response and fragility evaluation for an Eastern US NPP including soil-structure interaction effects[J].
Reliability Engineering and System Safety, 1988, 62: 197-214.
|
| [6] |
吕大刚, 于晓辉, 陈志恒. 钢筋混凝土框架结构侧向倒塌地震易损性分析[J].
哈尔滨工业大学学报, 2011, 43(6): 1-5.
LÜ Dagang, YU Xiaohui, CHEN Zhiheng. Lateral seismic collapse fragility analysis of RC frame structures[J]. Journal of Harbin Institute of Technology, 2011, 43(6): 1-5. |
| [7] |
HWANGH, 刘晶波. 地震作用下钢筋混凝土桥梁结构易损性分析[J].
土木工程学报, 2004, 37(6): 47-51.
HWANG H, LIU Jingbo. Seismic fragility analysis of reinforced concrete bridges[J]. China Civil Engineering Journal, 2004, 37(6): 47-51. |
| [8] |
高广艳. 单层球面网壳结构地震概率风险评估研究[D]. 哈尔滨: 哈尔滨工业大学, 2012.
GAO Guangyan. Research of seismic probability risk assessment for single-layer reticulated domes[D]. Harbin: Harbin Institute of Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10213-1013037957.htm |
| [9] |
范峰, 支旭东, 沈世钊.
网壳结构强震失效机理[M]. 北京: 科学出版社, 2014.
FAN Feng, ZHI Xudong, SHEN Shizhao. Failure mechanism of reticulated shells under earthquake[M]. Beijing: Science Press Ltd., 2014. |
| [10] |
田雨, 雷晓辉, 蒋云钟, 等. 水文模型参数敏感性分析方法研究评述[J].
水文, 2010(4): 9-12, 62.
TIAN Yu, LEI Xiaohui, JIANG Yunzhong, et al. Review on parameters sensitivity analysis methods of hydrological model[J]. Hydrology, 2010(4): 9-12, 62. |
| [11] |
戴国欣, 李龙春, 夏正中, 等. 建筑结构钢新材性参数的统计与分析[J].
建筑结构, 2000(4): 31-32.
DAI Guoxin, LI Longchun, XIA Zhengzhong, et al. Statistics and analysis of new material parameters of building structural steel[J]. Building Structure, 2000(4): 31-32. |
| [12] |
王丹. 钢框架结构的地震易损性及概率风险分析[D]. 哈尔滨: 哈尔滨工业大学, 2006.
WANG Dan. Seismic fragility analysis and probabilistic risk analysis of steel frame structures[D]. Harbin: Harbin Institute of Technology, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10213-2007034625.htm |
| [13] |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 建(构)筑物地震破坏等级划分: GB/T 24335—2009[S]. 南京: 凤凰出版社, 2009.
General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of the People's Republic of China. Classification of earthquake damage to buildings and special structures:GB/T 24335—2009[S]. Nanjing: Phoenix Publishing House, 2009. |
| [14] |
Applied Technology Council. Seismic performance assessment of buildings: report NO. FEMA P-58-1[R]. Washington:[s.n.], 2012,
|
| [15] |
POWELL G H, ALLAHABADI R. Seismic damage prediction by deterministic methods: Concepts and procedures[J].
Earthquake and Structural Dynamics, 1988, 16(5): 719-734.
DOI: 10.1002/(ISSN)1096-9845 |
| [16] |
欧进萍, 牛荻涛, 王光远. 多层非线性抗震钢结构的模型动力可靠性分析与设计[J].
地震工程与工程振动, 1990, 10(4): 27-37.
OU Jinping, NIU Ditao, WANG Guangyuan. Dynamics reliability analysis and design of multi-layer nonlinear seismic steel structure model[J]. Earthquake Engineering and Engineering Vibration, 1990, 10(4): 27-37. |
| [17] |
支旭东, 吴金妹, 范峰, 等. 考虑材料损伤累积单层柱面网壳在强震下的失效研究[J].
计算力学学报, 2008, 25(6): 770-775.
ZHI Xudong, WU Jinmei, FAN Feng, et al. Study on failure of single-layer cylindrical reticulated shells under strong earthquake considering material damage[J]. Chinese Journal of Computational Mechanics, 2008, 25(6): 770-775. |
| [18] |
李文博. 基于IDA方法的RC框架结构地震易损性分析研究[D]. 西安: 西安建筑科技大学, 2012.
LI Wenbo. Study on seismic fragility analysis of RC frame structures based on the IDA method[D]. Xi'an: Xi'an University of Architecture and Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10703-1012046055.htm |
 2017, Vol. 49
2017, Vol. 49


