2. 土木工程防灾国家重点实验室(同济大学),上海 200092
2. State Key Laboratory of Disaster Reduction in Civil Engineering (Tongji University), Shanghai 200092, China
在地震反应过程中,阻尼是影响反应结果的重要因素[1-2].为进行强震下结构的弹塑性时程反应分析,需要构建相应的阻尼矩阵.在各种阻尼模型中,Rayleigh阻尼由于计算简便而得到广泛应用.
采用矩阵表达,Rayleigh阻尼矩阵C可表达为质量矩阵M和刚度矩阵K的线性组合,即
| $ \mathit{\boldsymbol{C}}=\alpha \mathit{\boldsymbol{M}}+\beta \mathit{\boldsymbol{K}}, $ | (1) |
式中α和β分别为质量和刚度比例阻尼系数.α和β这两个系数可以通过指定两个参考频率(ωi和ωj)及其阻尼比(ζi*和ζj*)进行计算.显然,Rayleigh阻尼除两阶参考频率的阻尼比外,其他各阶模态的阻尼比有一定的误差存在.因此,所构造的Rayleigh阻尼是否合理依赖于选取的两个参考频率是否合理.在结构地震反应分析时,Rayleigh阻尼参考频率的选取有三类常用方法.
第一类方法是直接从结构的动力特性角度选择参考频率.Idriss等[3]直接利用体系基频ω1建立阻尼矩阵,此时所构造的Rayleigh阻尼高估了除基频以外的所有阻尼,从而导致结构动力反应偏小[4].对于简单的建筑结构,常用两个低阶自振频率作为参考频率[5].但对复杂结构而言,对结构有显著贡献的模态数目多达几百阶[6].此时,如果用两个低阶模态建立Rayleigh阻尼矩阵将使结构高阶模态的阻尼比偏大,从而导致低估结构的地震反应.Chopra[7]定性的指出,选择的两阶参考频率应使对结构反应有显著贡献模态的阻尼比取值合理.Clough等[8]建议ωi=ω1,ωj从对结构动力反应有显著贡献的高阶振型中选取.Youssef等[9]的计算结果表明,最优参考频率的阶数随土层深度变化而变化.
第二类方法是令ωi=ω1,第二个参考频率ωj由地震波的频谱特性进行确定.Hudson等[10]令ωj为地震波卓越频率ωe和结构基频的奇数倍.即
| $ {{\omega }_{\mathit{j}}}\rm{=}\mathit{n}{{\omega }_{\rm{1}}}, $ | (2) |
式中n为大于ωe/ω1的奇数.楼梦麟等[11]建议以输入地震波加速度反应谱的峰值频率作为ωj进行深覆盖土层的地震反应计算.
第三类方法采用优化算法直接得到Rayleigh阻尼系数.杨大彬等[12]以振型的峰值应变能系数作为权重函数,建立了加权最小二乘法.潘旦光等[13-14]分别以结构峰值位移误差和基底剪力误差最小为目标函数,提出了一种求解Rayleigh阻尼系数的优化求解方法.
为比较上述三类Rayleigh阻尼系数计算方法的特点及对结构动力反应的影响.本文将以大跨网壳结构水平方向和竖向地震反应为例,讨论不同方法所得阻尼矩阵对网壳顶点位移及基底剪力的影响.除此以外,本文还从Rayleigh阻尼构建角度讨论了地震波主要频率成分及其选取范围的问题.
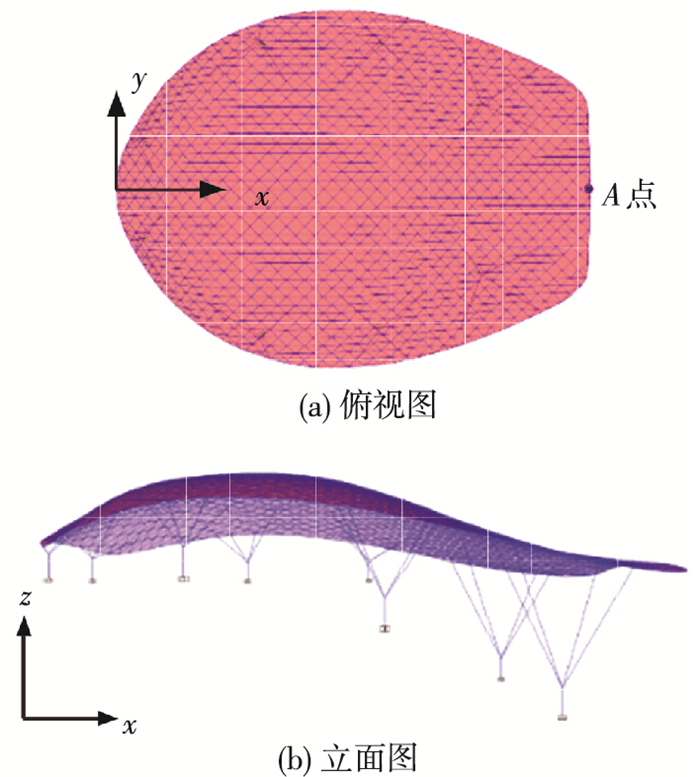
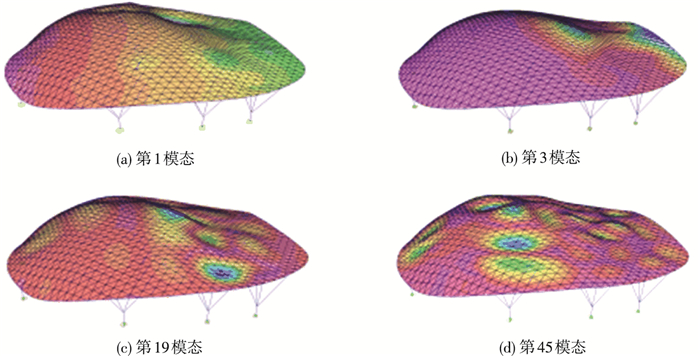
1 大跨网壳有限元模型及输入地震波 1.1 有限元模型结构计算模型如图 1所示,上部为85.2 m长,61.8 m宽单层网壳结构,下部由8组支架支撑整个结构.结构平面关于x轴对称,关于y轴不对称,z为竖向坐标.结构主要构件如下:网壳内部杆件和环梁分别为300 mm×50 mm×8 mm×12 mm和1 000 mm×600 mm×30 mm×30 mm的空心方管,下部斜撑和底柱分别为300 mm×20 mm和800 mm×35 mm的空心圆管.所有杆件材料为Q235,采用梁单元进行建模.模型的模态特征如表 1所示.表中ry和rz分别表示y和z方向的振型参与质量比,sy和sz分别表示y和z方向的累积振型参与质量比.部分典型模态图如图 2所示.并设各阶模态的阻尼比为0.02.
|
图 1 网壳有限元模型 Figure 1 Finite element model of reticulated shell |
| 表 1 固有频率及振型参与质量比 Table 1 Natural frequencies and modal participation mass ratios |
|
图 2 部分模态图 Figure 2 Part of mode shapes |
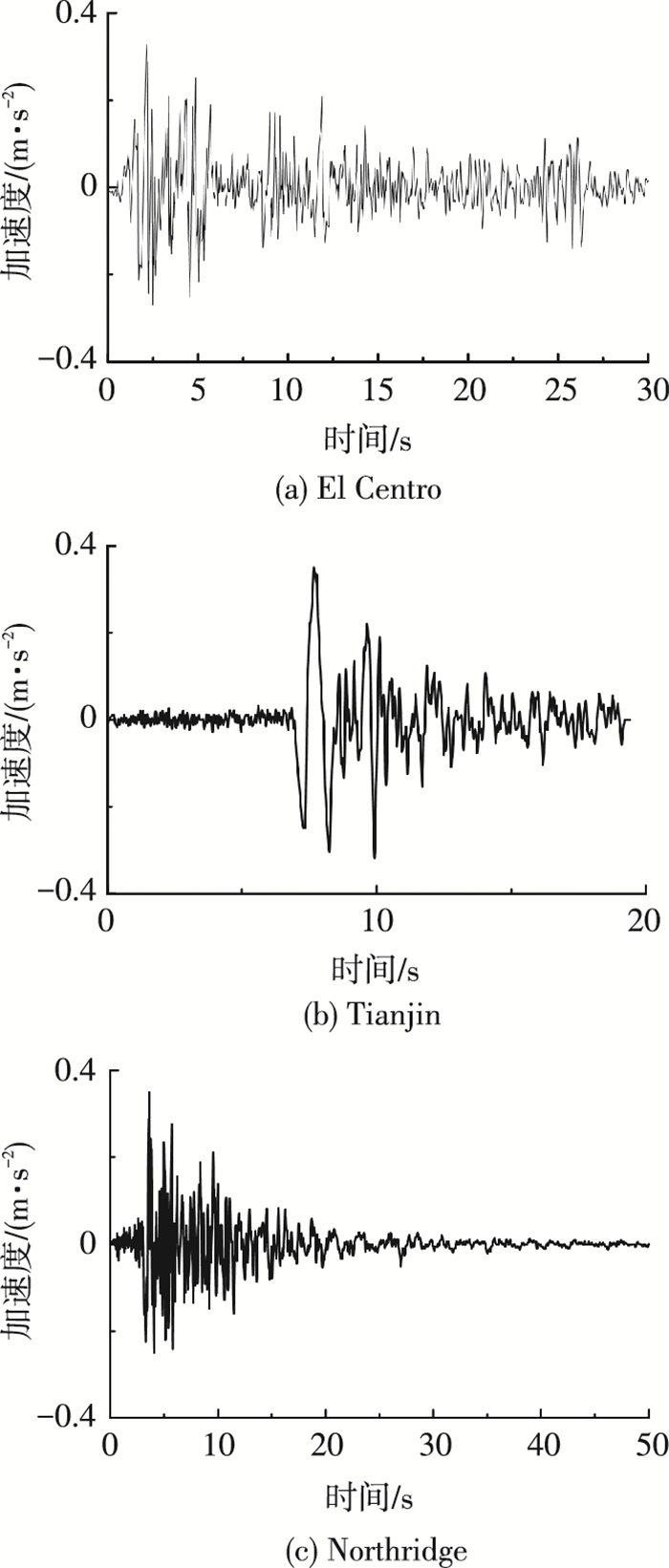
为比较不同类型地震波对Rayleigh阻尼系数计算的影响,选用表 2中的3条不同场地类型地震波分别作为柱根部的水平和竖向地震输入.输入地震波的加速度时程如图 3所示,加速度时程的幅值统一调整为0.35 m/s2.
| 表 2 地震波 Table 2 Earthquake waves |
|
图 3 地震波加速度时程 Figure 3 Acceleration histories of earthquake waves |
由模态分析可知,单层网壳结构在y方向(水平)地震输入时,前45阶模态的振型参与质量即超过90%,第一阶模态的反应贡献具有绝对统治地位.对于z方向(竖向)地震输入时,前205阶模态的振型参与质量超过90%,第三阶模态的反应贡献最大,但不具有统治地位.对于水平地震反应,结构的显著贡献模态少;而竖向地震反应,结构的显著贡献模态多,且没有具有绝对统治地位的模态.同时,在水平地震反应时,结构的第一个显著贡献模态的频率小于大部分地震波的卓越频率,而竖向地震反应时,结构的第一个显著贡献模态的频率高于部分地震波的卓越频率,因此,讨论y方向和z方向的地震反应,相当于讨论了两种结构类型下Rayleigh阻尼系数的计算问题.不同方法计算阻尼系数的差别在于两个参考频率选取的不同,为此,下面讨论单层网壳结构y方向和z方向地震反应时三类方法所得的参考频率及对结构地震反应的影响.
2.1 第一类方法对于y方向地震输入,一种是根据经验选择ωi=ω1和ωj=ω19(记为i=1 & j=19),另一种是直接令ωi=ω1和ωj=ω2(i=1 & j=2).对于z方向地震输入,分别考虑两种组合ωi=ω3和ωj=ω45(i=3 & j=45)及ωi=ω1和ωj=ω2(i=1 & j=2).并在后面的讨论中将这种方法称为传统方法.
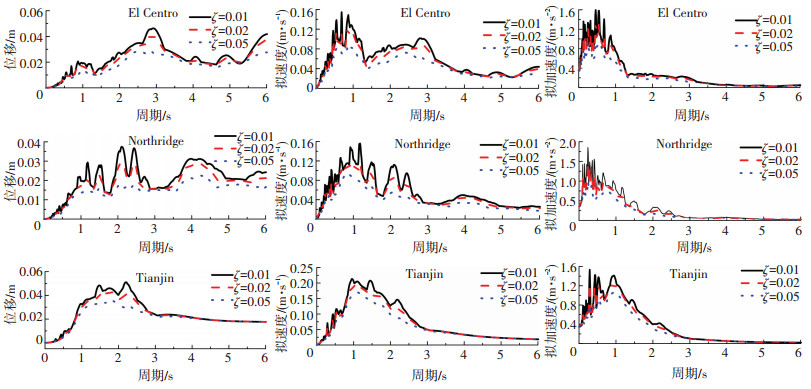
2.2 第二类方法在第二类方法中,y方向和z方向地震输入的第一个参考频率分别选为ω1和ω3.第二个参考频率可基于反应谱和Fourier谱进行选择.图 4为3条地震波的位移、拟速度和拟加速度反应谱.
|
图 4 地震波反应谱 Figure 4 Response spectra of earthquake waves |
在利用反应谱选择Rayleigh阻尼第二个参考频率时,常直接选取反应谱峰值频率[15].但这种方法存在的一个问题是:当结构的基频高于反应谱峰值频率时,构建的Rayleigh阻尼将使所有的高阶模态阻尼比大于真实的阻尼比,从而使计算结果偏小,这一点在位移反应谱中尤其明显,因为位移反应谱的峰值常出现在长周期.譬如,自振周期在0~6 s范围内,El Centro、Northridge和Tianjin波的位移反应谱峰值频率分别为0.352、0.410和0.568 Hz,这些峰值频率都小于基频,此时,都无法构造出合理的Rayleigh阻尼.事实上,反应谱反映的是在一个确定地震波作用下不同自振周期单自由度体系的最大反应,然后,以一定组合规则得到结构的反应.结构高阶模态的周期Ti都是小于基频周期T1的,即Ti<T1 (i=1, 2, …).因此,[0, T1]区间的反应谱才参与结构反应的计算.从这个角度看,以[0, T1]区间内反应谱的峰值频率作为第二个参考频率更合理.表 4和表 5中列出的拟加速度反应谱峰值频率fRa、拟速度反应谱峰值频率fRv和位移反应谱峰值频率fRd都是指[0, T1]区间内的峰值频率.
| 表 4 y方向地震输入下的参考频率 Table 4 eference frequencies under the y direction seismic input |
| 表 5 z方向地震输入下的参考频率 Table 5 Reference frequencies under the z direction seismic inpu |
考虑到多自由度体系是一系列单自由度体系反应的叠加,因此,部分学者将地震波的主要频率定义为反应谱形心的频率[15].反应谱的形心频率fRg-i定义如下
| $ \frac{1}{{{f}_{{\rm{Rg}}-i}}}=\frac{\int_{0}^{{{T}_{\rm{R}}}}{T{{S}_{i}}\left( \zeta, T \right)\rm{d}\mathit{T}}}{\int_{0}^{{{T}_{\rm{R}}}}{{{S}_{i}}\left( \zeta, T \right)\rm{d}\mathit{T}}}, $ | (3) |
式中:Si(ζ, T)为反应谱,i分别取位移、拟速度和拟加速度.显然fRg-i是积分范围TR的函数.图 5为不同地震波反应谱fRg-i随积分区间变化的曲线.由图可知,随着积分区间的增加,形心点的频率逐步降低.这是长周期部分反应谱影响的必然结果.由于只有[0, T1]区间的反应谱参与结构反应的计算,因此,计算形心频率的反应谱范围定义为[0, T1]更合理.表 4和表 5中列出拟加速度反应谱形心频率fRg-a、拟速度反应谱形心频率fRg-v和位移反应谱形心频率fRg-d都是指[0, T1]基本区间不同地震波反应谱的形心频率.

|
图 5 反应谱形心频率 Figure 5 Centroid frequencies of response spectra |
图 6为不同地震波Fourier谱.Fourier谱表明地震波中含有哪些频率分量,及哪些频率分量振幅大.因此,将分量振幅最大的频率称为卓越频率,并记为Fourier谱峰值频率fF.实际地震波的Fourier谱呈剧烈起伏的锯齿状,为避免Fourier谱中个别尖刺的影响,常将平滑化方法所得的峰值频率作为地震波卓越频率.本文将平滑化后Fourier谱的峰值频率记为fP.图 6中的平滑化曲线是采用矩形脉冲窗的结果,窗的带宽取为1.2 Hz.
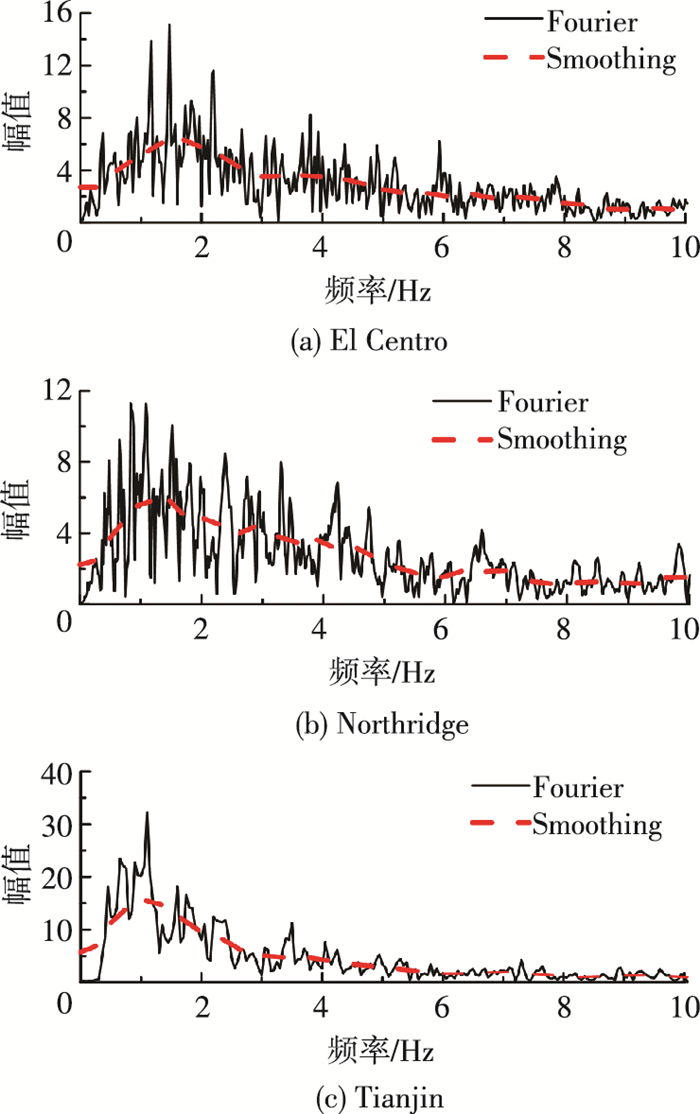
|
图 6 地震波Fourier谱 Figure 6 Fourier spectra of earthquake waves |
在得到地震波的卓越频率后,可采用式(2)计算Rayleigh阻尼系数.当ωe取为Fourier谱的峰值频率fF时,称为Ⅰ-1方法;当ωe取为平滑化Fourier谱的峰值频率fP时,称为Ⅰ-2方法.且当ωe<ω1时,令n=1.
2.3 第三类方法对于第三类方法,以文献[14]提出的约束优化解法作为对比.该方法首先建立代数方程组:
| $ \left[{\begin{array}{*{20}{c}} \mathit{\boldsymbol{G}}&{{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_s}}\\ {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_s^{\rm{T}}}&0 \end{array}} \right]\left\{ \begin{array}{l} \mathit{\boldsymbol{a}}\\ \lambda \end{array} \right\} = \left\{ \begin{array}{l} \mathit{\boldsymbol{H}}\\ \zeta _s^ * \end{array} \right\}, $ | (4) |
式中:G= ΩwΩT,H= Ωwy,w=[wij],wij=ρijMiMjS′a×(ζi, ωi)S′a(ζj, ωj),y={ζ1*, ζ2*, …, ζN*}T,ζi*(i=1, 2, …, N)是指各阶模态的精确阻尼比.
Ω=[Ω1, Ω2, …, ΩN],a={α β}T为Rayleigh阻尼系数组成的向量,Ωi=0.5{ωi-1 ωi}T(i=1, 2, …, N)中的ωi为结构的第i阶固有频率,y方向和z方向激振下N分别取为45和205.S′a(ζn*, ωn)为拟加速度反应谱关于阻尼的导数,Mi为第i阶模态的振型参与质量百分比,Ωs=0.5{ωs-1 ωs}T是指约束第s阶的模态阻尼比等于ζs*.对于y方向和z方向地震输入,约束模态分别取为ω1和ω3.
根据以上讨论,共形成12种Rayleigh阻尼系数的计算方法,其中传统方法在算例比较时,采用两种频率组合.表 3列出了各种计算方法的简化名称和所对应的类型.下面讨论各种方法所得Rayleigh阻尼对单层网壳结构地震反应的影响.
| 表 3 Rayleigh阻尼系数计算方法 Table 3 Estimation methods of Rayleigh damping coefficients |
为比较不同方法的计算误差,进行结构的线弹性地震反应分析.同时,以前300阶模态振型分解时程分析方法的计算结果为精确解,记为r*,采用Rayleigh阻尼模型所得的近似解记为r,则Rayleigh阻尼模型计算结果的相对误差为
| $ \mathit{e} = \frac{{\left| r \right| - \left| {{r^ * }} \right|}}{{\left| {{r^ * }} \right|}} \times 100\% . $ | (5) |
在m条地震波作用下,各反应量的平均误差可采用以下两式进行统计:
| $ {{\mathit{\bar e}}_{\rm{r}}} = \frac{1}{m}\sum\limits_{i = 1}^m {{e_i}, \;} {{\mathit{\bar e}}_{\rm{a}}} = \frac{1}{m}\sum\limits_{i = 1}^m {\left| {{e_i}} \right|.} $ | (6) |
式中:er用于度量不同方法所得计算结果是偏大还是偏小,而ea用来表示这个方法的计算精度.
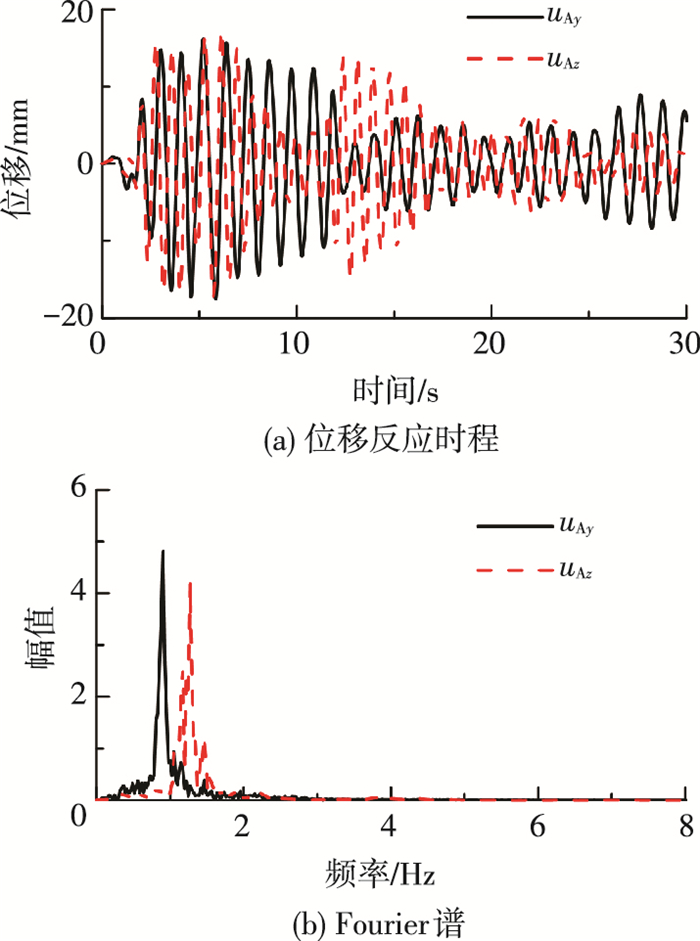
3.2 不同Rayleigh阻尼模型计算误差El Centro、Northridge和Tianjin三条地震波分别沿y方向(水平)和z方向(竖向)输入下,前述12种方法的参考频率如表 4和表 5所示.在y方向地震输入时,仅统计y方向的地震反应,z方向地震输入时,仅统计z方向的地震反应.图 1中A点的位移计算误差和基底剪力误差如表 6~9所示.El Centro波作用下A点位移反应的精确解及其Fourier谱如图 7所示,基底剪力的精确解及其Fourier谱如图 8所示.表和图中的uAy和uAz分别表示A点的y方向和z方向的位移.Fy和Fz分别表示y方向和z方向的基底剪力.
| 表 6 y方向地震输入下uAy的相对误差 Table 6 The relative error of displacement uAy under the y direction seismic input |
| 表 7 z方向地震输入下uAz的相对误差 Table 7 The relative error of displacement uAz under the z direction seismic input |
| 表 8 y方向地震输入下基底剪力Fy的相对误差 Table 8 The relative error of base shear Fy under the y direction seismic input |
| 表 9 z方向地震输入下基底剪力Fz的相对误差 Table 9 The relative error of base shear Fz under the z direction seismic input |
|
图 7 Centro波作用下A点的位移反应时程及Fourier谱 Figure 7 Time histories and Fourier spectra of point A displacement under the El Centro wave |

|
图 8 Centro波作用下基底剪力反应时程及Fourier谱 Figure 8 Time histories and Fourier spectra of base reactions under the El Centro wave |
由计算结果可看出:
1) 除i=1 & j=2组合的传统方法进行竖向地震反应计算外,其余方法所得A点位移uAy和uAz的平均误差基本相同.对于y方向地震输入,观察表 1和图 7的结果可以发现,第一模态的位移反应远大于其他模态的反应.对于z方向地震输入,虽然第三模态的振型参与质量的优势不是特别明显,但是,uAz的Fourier谱表明,第三模态的位移反应具有绝对主导地位.此时,对于Rayleigh阻尼矩阵而言,当y方向地震输入时,只要ζ1=ζ1*;当z方向地震输入时,只要ζ3=ζ3*;uAy和uAz的计算精度即可满足精度要求.而任意选择前两阶模态组合计算Rayleigh阻尼系数,进行z方向地震反应计算,计算误差大且偏小.
2) 对于基底剪力Fy和Fz,以fRv、fRd、fRg-v、fRg-d为第二参考频率的计算结果都偏小.对比反应谱的峰值频率和形心频率可以发现fRa>fRv>fRd,以及fRg-a>fRg-v>fRg-d.这是由于反应谱在大于2 Hz区域为加速度敏感区,小于0.3 Hz为位移敏感区,中间区段为速度敏感区[7].而由图 8基底剪力的Fourier谱可知,高阶模态对基底剪力的反应也有显著贡献.譬如f19=2.905 Hz和f45=4.443 Hz模态的反应分别对Fy和Fz有显著影响,而基于速度反应谱的fRv、fRg-v和位移反应谱的fRd、fRg-d的第二个参考频都远小于f19和f45,导致这两阶模态的阻尼比偏大而低估了高阶模态的反应.基于加速度反应谱峰值频率和形心频率的计算误差相对较小.
3) fF作为第二个参考频的计算结果偏小.这是由于Fourier谱和拟速度反应谱类似,因此,fF和fRv的计算结果也类似.以平滑化的峰值频率fP作为第二个参考频的计算结果要略优于fF的计算结果,但无法改变计算结果偏小的特点.同时,当fF或fP小于结构的基频时,直接用卓越频率作为第二个参考频率的计算误差更大.这是由于这种方法除基频的阻尼比外,其余模态的阻尼比都大于精确解而导致计算结果偏小.因此,对于地震波卓越频率小于结构基频的地震波,采用地震波卓越频率作为参考频率不合理.
4)Ⅰ-2方法的平均误差小于Ⅰ-1方法,这表明采用平滑化Fourier谱所得卓越频率进行Idriss方法[10]第二个频率的计算更合理.而且,由于fF易受Fourier谱中个别低频尖刺的影响,而使计算结果离散性大.同时,当地震波的卓越频率小于结构的基频时,此时,Idriss方法实际上就是基于基频建立阻尼矩阵,Rayleigh阻尼高估了高阶模态的阻尼比,由此使结构的地震反应偏小,因此,当地震波的卓越频率小于结构的基频时,Ⅰ-1和Ⅰ-2方法都是不合理的.当地震波的卓越频率大于结构的基频时,可采用Ⅰ-2方法建立Rayleigh阻尼.
5) 对于优化方法,无论是y方向地震输入还是z方向地震输入,由于优化算法中考虑了结构动力特性、地震波频率特性的影响,因此,对于两个方向的地震输入和所有地震波的计算结果误差都小且稳定.而且,优化方法是直接得到Rayleigh阻尼系数,避免了人为选择两阶参考频率的任意性,适用于不同工程结构的Rayleigh阻尼构建.
6) 对于传统方法,本文所选的y方向和z方向的频率组合i=1 & j=19和i=3 & j=45实际上和优化分析方法的频率基本相同,因此,对于富有经验的计算人员,直接选取两阶合理的参考频率用于Rayleigh阻尼计算也是可行的.但是,任意选择前两阶模态进行Rayleigh阻尼计算所得计算结果偏小,且绝对误差最大,是不合理的计算方法.
4 结论在大型复杂结构的非线性地震反应分析时,常需建立Rayleigh阻尼矩阵进行直接积分法计算.由于参与结构振动的模态多且复杂,因此,如何选取合理的参考频率是一个需要仔细斟酌的事情.本文以一个长85.2 m,宽61.8 m的大跨屋盖为例,对比分析了12种国内外Rayleigh阻尼系数计算方法对计算结果的影响,由理论分析和数值计算可得出以下结论:
1) 对于第一类方法,工程技术人员如果对结构的动力反应有充分认识,可直接指定两阶参考频率.但是,任意选择前两阶模态进行Rayleigh阻尼计算,易造成计算结果偏小,是不合理的计算方法.
2) 对于第二类方法,建议采用[0, T1]区间的拟加速度反应谱峰值频率或形心频率、Ⅰ-2方法作为Rayleigh阻尼系数计算的第二个参考频率.
3) 优化方法所得Rayleigh阻尼系数是综合考虑结构的动力特性、输入地震波频谱特性的综合结果,直接得到Rayleigh阻尼系数,避免了基于经验指定两阶频率的任意性,且计算误差较小,适合于工程结构的计算与分析.
| [1] |
沈聚敏, 周锡元, 高小旺.
抗震工程学[M]. 北京: 中国建筑工业出版社, 2002.
SHEN Jumin, ZHOU Xiyuan, GAO Xiaowang. Earthquake engineering[M]. Beijing: China Architecture & Building Press, 2002. |
| [2] |
翟长海, 谢礼立, 张茂花. 阻尼对工程结构等延性地震抗力谱的影响分析[J].
哈尔滨工业大学学报, 2007, 38(10): 1705-1708.
ZHAI Changhai, XIE Lili, ZHANG Maohua. Influence analysis damping on constant-ductility seismic resistance spectra for seismic design of structures[J]. Journal of Harbin institute of technology, 2007, 38(10): 1705-1708. |
| [3] |
IDRISS I M, LYSMER J, HWANG R, et al. Quad 4: a computer program for evaluating the seismic response of soil structures by variable damping finite element procedures[R]. Berkeley: University of California, 1973.
|
| [4] |
邹德高, 徐斌, 孔宪京. 瑞利阻尼系数确定方法对高土石坝地震反应的影响研究[J].
岩土力学, 2011, 32(3): 797-803.
ZOU Degao, XU Bin, KONG Xianjing. Study of influence of different methods for calculating Rayleigh damping coefficient on high earth-rock dam seismic response[J]. Rock and Soil Mechanics, 2011, 32(3): 797-803. |
| [5] |
周国良, 李小军, 刘必灯, 等. 大质量法在多点激励分析中的应用、误差分析与改进[J].
工程力学, 2011, 28(1): 48-54.
ZHOU Guoliang, LI Xiaojun, LIU Bideng, et al. Error analysis and improvements of large mass method used in multi-support seismic excitation analysis[J]. Engineering Mechanics, 2011, 28(1): 48-54. DOI: 10.6052/j.issn.1000-4750.2009.07.0456 |
| [6] |
潘旦光, 靳国豪, 高莉莉. 大跨斜拉桥Rayleigh阻尼系数的约束优化解[J].
振动与冲击, 2014, 33(16): 34-41.
PAN Danguang, JIN Guohao, GAO Lili. Constraint optimal solution of Rayleigh damping coefficients for long-span cable-stayed bridges[J]. Journal of Vibration and Shock, 2014, 33(16): 34-41. |
| [7] |
CHOPRA A K.
Dynamics of structures: theory and applications to earthquake engineering[M]. New Jersey: Englewood Cliffs, Prentice-Hall, 1995.
|
| [8] |
CLOUGH R W, PENZIEN J.
Dynamics of structures[M]. New York: Mc-Graw Hill Inc, 1993.
|
| [9] |
YOUSSEF M A, HASHASH D P. Viscous damping formulation and high frequency motion propagation in nonlinear site response analysis[J].
Soil Dynamics and Earthquake Engineering, 2001, 22: 611-624.
|
| [10] |
HUDSON M, IDRISS I M, BEIKAE M. User manual for QUAD4m: A computer program to evaluate the seismic response of soil structures using finite element procedures and incorporating a compliantbase[D]: Berkeley: University of California, 1994.
|
| [11] |
楼梦麟, 邵新刚. 应用通用程序计算深覆盖土层地震反应的几个问题[J].
振动与冲击, 2015, 34(4): 63-68, 109.
LOU Menglin, SHAO Xin'gang. Several problems in seismic response calculation of soil layer with deep deposit using general software[J]. Journal of Vibration and shock, 2015, 34(4): 63-68, 109. |
| [12] |
YANG Dabin, ZHANG Yigang, WU Jinzhi. Computation of Rayleigh damping coefficients in seismic time-history analysis of spatial structures[J].
Journal of the International Association for Shell and Spatial Structures, 2010, 51(2): 125-135.
|
| [13] |
潘旦光. 直接确定Rayleigh阻尼系数的一种优化方法[J].
工程力学, 2013, 30(9): 16-21.
PAN Danguang. An optimization method for the direct determination of Rayleigh damping coefficients[J]. Engineering Mechanics, 2013, 30(9): 16-21. |
| [14] |
PAN D G, CHEN G D, GAO L L. A constrained optimal Rayleigh damping coefficients for structures with closely-spaced natural frequencies in seismic analysis[J].
Advances in Structural Engineering, 2017, 20(1): 81-95.
DOI: 10.1177/1369433216646007 |
| [15] |
楼梦麟, 邵新刚. 深覆盖土层Rayleigh阻尼建模问题讨论[J].
岩土工程学报, 2013, 35(7): 1272-1279.
LOU Menglin, SHAO Xingang. Discussion on modeling issues of Rayleigh damping matrix in soil layer with deep deposit[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(7): 1272-1279. |
 2017, Vol. 49
2017, Vol. 49


