2. 哈尔滨工业大学 土木工程学院,哈尔滨 150090
2. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China
螺栓球节点是一种常用的空间网格结构节点形式,其工厂化生产、安装速度快等特点符合装配式建筑的要求,在工程设计与施工中得到了广泛的应用.但是由于螺栓球节点的组成构件较多,在实际安装中容易存在诸多施工缺陷,如高强螺栓拧入长度不足、杆件初始弯曲等[1].其中高强螺栓拧入长度不足是一种较为常见的施工缺陷,规范《空间网格结构技术规程》[2]中要求高强螺栓的拧入长度在1.1倍螺栓直径左右,实际工程中由于构件质量和安装缺陷等原因常常不能满足规范要求的拧入长度,因此造成的工程事故不在少数.1995年天津某地毯厂网架发生坍塌,对事故原因进行分析发现部分高强螺栓的拧入长度不足,导致高强螺栓发生螺纹破坏而从螺栓球中拔出[3].2005年内蒙古某公司发电厂汽机间网架在施工过程中未按要求架设临时支撑,使网架产生较大变形,导致高强螺栓与螺栓孔对接偏差较大,高强螺栓存在假拧紧情况,因此造成坍塌事故[4].可见,高强螺栓拧入长度不足对螺栓球节点的受力性能影响较大,对结构安全性造成严重的影响.以往的研究主要关注螺栓球节点的半刚性[5-6]及其在单层网壳结构中的适用性[7-8],对高强螺栓拧入长度不足下的节点受力性能研究较少.在数值模拟方面,Chenaghlou等[9]曾建立了螺栓球节点有限元分析模型,但对节点的螺纹部分未做精细化建模,在螺纹传力上与实际情况有一定差距.因此,有必要建立带有螺纹的螺栓球节点精细化模型来研究高强螺栓拧入长度不足对节点受力性能的影响.
本文首先建立带有螺纹的螺栓球节点精细化有限元模型,对现有节点试验进行模拟分析,验证模拟方法的准确性.通过改变螺纹的啮合数模拟高强螺栓拧入长度不足的施工缺陷,对M20、M24、M27三种高强螺栓规格对应节点的力学性能及其工作破坏机理进行研究,给出高强螺栓拧入长度对螺栓球节点力学性能影响规律,为螺栓球节点的施工控制及相似结构的安全性能评估提供技术参考.
1 节点精细化模拟方法及分析方案 1.1 模型建立节点模型基于ANSYS平台建立,构件材料按规范《钢网架螺栓球节点用高强度螺栓》[10]要求选取,螺栓球采用45号圆钢,高强螺栓采用40Cr,套筒、锥头、钢管采用Q235钢,具体材料参数见表 1,本构关系采用双折线随动强化模型.由于螺纹破坏主要为剪切变形且变形较大,故采用3D8节点SOLID185单元来模拟各构件.
| 表 1 材料参数 Table 1 Material parameters |
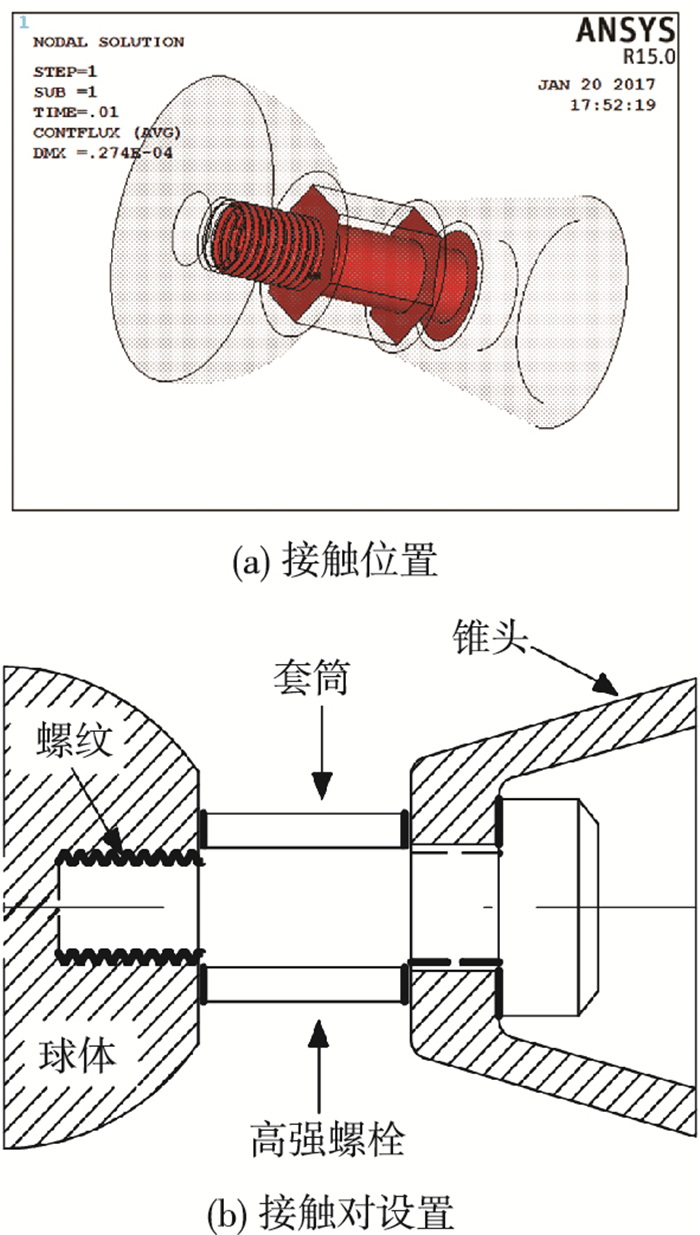
为真实模拟节点各构件之间受力,防止模型因为大变形而发生单元渗透,本文选取ANSYS中提供的面-面接触单元CONTA174和TARGE170来模拟接触面和目标面.接触面设置见图 1,具体接触对设置见表 2.通过改变接触单元实常数来调整接触刚度,减小渗透.例如:通过增大法向接触刚度系数FKN来提高接触刚度,从而保证计算的速度和精确性.
|
图 1 螺栓球节点接触设置 Figure 1 Contact setting of bolt-ball joint |
| 表 2 接触对设置 Table 2 Contact pairs setting |
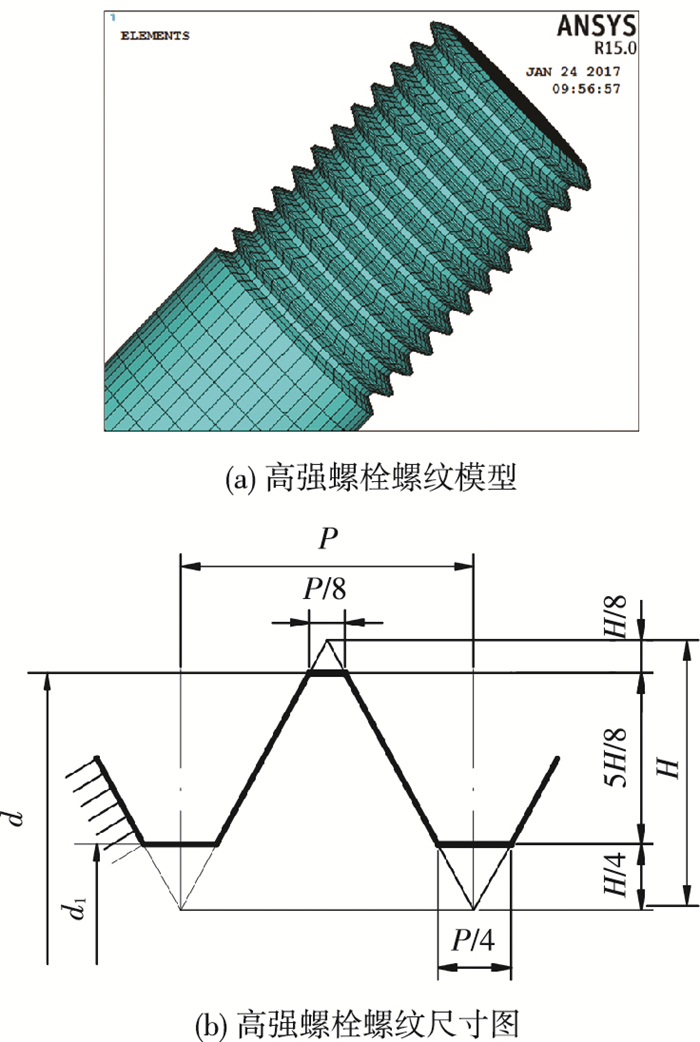
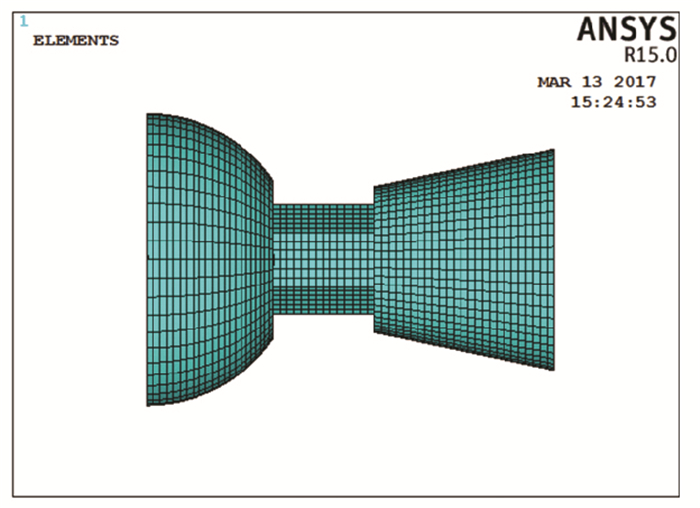
本文按照规范《普通螺纹基本尺寸》[11]规定的螺纹尺寸对高强螺栓的螺纹进行精细化建模见图 2,具体尺寸见表 3, 最终节点精细化模型见图 3.
|
图 2 螺纹图示 Figure 2 Sketch maps of threads |
| 表 3 螺纹参数 Table 3 Threads parameter |
|
图 3 有限元模型 Figure 3 Finite element model |
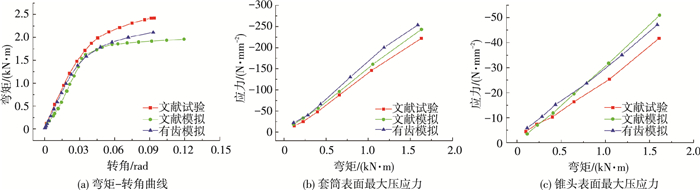
为验证数值模拟的准确性,采用上述精细化模拟方法对文献[12]试验进行分析.以M24螺栓球节点为例,模拟结果与试验结果对比见图 4.模拟结果与试验结果吻合良好,由于可以真实地考虑高强螺栓和螺栓球之间的螺纹啮合传力,本文模型的模拟结果更加贴近试验,能够更好地模拟节点的受力性能.
|
图 4 M24节点模拟与文献试验比对 Figure 4 M24 joint simulations in comparison with literature experiments |
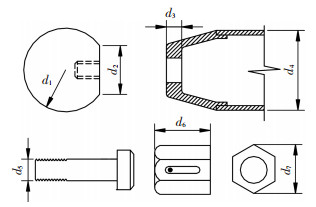
为研究高强螺栓拧入长度不足对节点抗弯性能及抗拉性能的影响,本文对工程中常用的M20、M24、M27三种高强螺栓规格对应的节点进行分析,构件示意见图 5,具体尺寸见表 4.为方便表述,后文对不同拧入长度分析模型的命名方式为:M高强螺栓直径-拧入螺纹数,如M20-9表示M20节点高强螺栓拧入9个螺纹.具体分析方案见表 5.
|
图 5 节点构件尺寸示意 Figure 5 Sketch maps of joint component sizes |
| 表 4 节点尺寸 Table 4 Joints sizes |
| 表 5 分析方案 Table 5 Analysis plans |
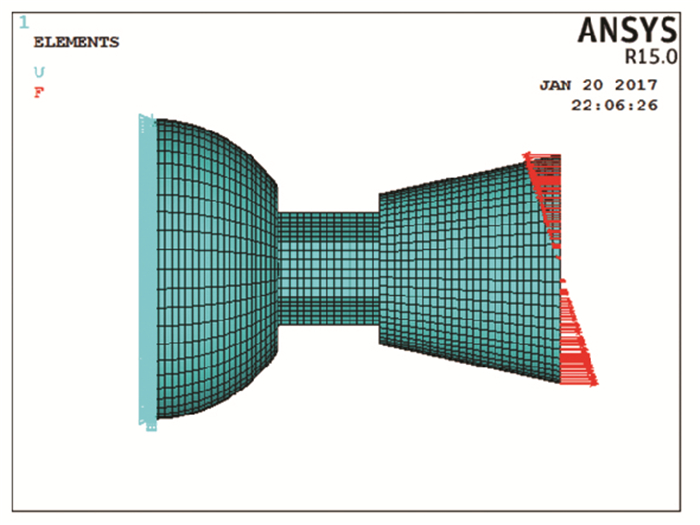
作为典型的半刚性节点,螺栓球节点的抗弯能力已在实际工程中得以应用[13].而高强螺栓拧入长度不足对节点抗弯性能的影响不可忽视,因此,以下将对高强螺栓拧入长度不足时的螺栓球节点抗弯性能进行分析,分析模型见图 6.
|
图 6 有限元模型 Figure 6 Finite element model |
以M20节点为例,通过分析发现,由于高强螺栓拧入长度的不同,螺栓球节点在弯矩作用下存在三种工作及破坏模式.
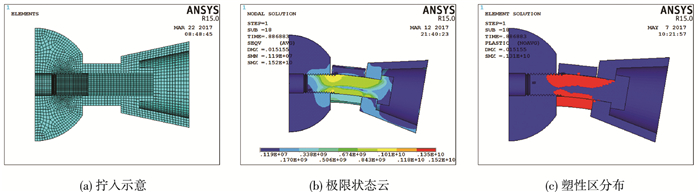
第一种为高强螺栓拧满时(M20-9),其工作机理见图 7.初始阶段套筒与球体、锥头之间闭合无空隙见图 7(a).在弯矩作用下节点由套筒和高强螺栓协同抵抗弯矩.极限状态时各构件变形及应力水平见图 7(b),提取节点塑性区域分布图见图 7(c),由图可知,高强螺栓和套筒大面积进入塑性,节点表现为高强螺栓的弯曲破坏和套筒的受压破坏,节点变形较小.
|
图 7 M20-9节点工作机理示意 Figure 7 M20-9 joints' working principle |
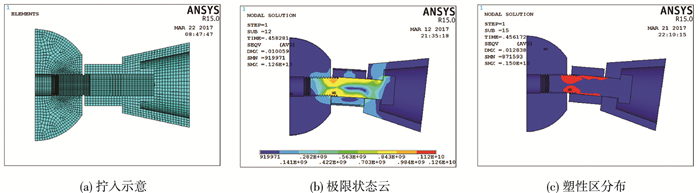
第二种为高强螺栓拧入长度轻度不足时(M20-8),其工作机理见图 8.初始阶段套筒与球体、锥头并无接触件图 8(a),高强螺栓单独抵抗弯矩.当节点转角达到一定程度,套筒与球体、锥头发生接触,高强螺栓与套筒协同工作抵抗弯矩,此时高强螺栓应力较大,套筒应力较小.极限状态时各构件变形及应力水平见图 8(b),提取节点塑性区域分布见图 8(c),高强螺栓大面积进入塑性,节点表现为高强螺栓的弯曲破坏,节点变形相对较大.
|
图 8 M20-8节点工作机理示意 Figure 8 M20-8 joints' working principle |
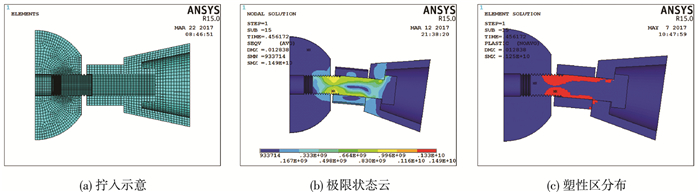
第三种为高强螺栓拧入长度严重不足时(M20-7),其工作机理见图 9.由于高强螺栓拧入长度严重不足见图 9(a),套筒与球体之间间隙较大.随着弯矩的增大,直至节点破坏,套筒亦无法与球体发生接触,全程由高强螺栓自身抵抗弯矩.极限状态时各构件变形及应力水平见图 9(b),提取节点塑性区域分布图见图 9(c),由图可知,高强螺栓大面积进入塑性,最终表现为高强螺栓的弯曲破坏,节点变形最大.
|
图 9 M20-7节点工作机理示意 Figure 9 M20-7 joints' working principle |
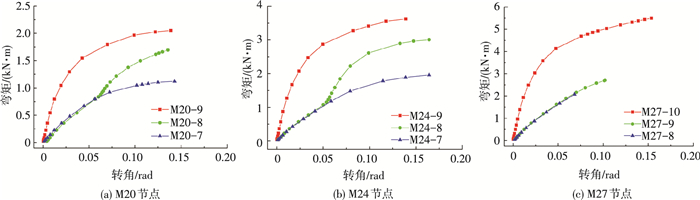
绘制节点弯矩-转角曲线见图 10,可以看出,与其工作模式对应,随着拧入长度的不同螺栓球节点弯矩-转角曲线分三种形式.第一种模式为高强螺栓拧满时,由于套筒与高强螺栓全程协同抵抗弯矩,节点转动刚度较大,其极限承载力最高;第二种模式为拧入长度轻度不足时,高强螺栓首先承受大部分弯矩,节点初始刚度下降.当高强螺栓转角达到一定程度时,套筒与球体、锥头发生接触,套筒与高强螺栓协同抵抗弯矩,节点刚度有一定提升,故弯矩-转角曲线出现明显提升,其承载力相较于第一种模式有所降低;第三种模式为拧入长度严重不足时,由于初始间隙较大,套筒全程未与球体、锥头发生接触,由高强螺栓自身抵抗弯矩,节点初始刚度降低明显,极限承载力最低.且分析可知,M20、M24节点的弯矩-转角曲线出现上述三种模式,而M27节点只出现第一种及第三种模式,即螺纹啮合数减少1个时,M27承载力及刚度下降明显,其抗弯性能对拧入误差更为敏感.
|
图 10 高强螺栓不同拧入长度下弯矩-转角曲线 Figure 10 Moment-rotation curves of high-strength bolts under different inserted depth |
参考文献[14],本文取弹性阶段弯矩与转角呈线性关系的切线斜率为初始刚度Ki,节点达到极限状态时对应的弯矩为极限弯矩Mu.三种节点在不同拧入长度下的初始刚度和极限弯矩见表 6.可以看出,当螺纹啮合数减少1个时,M20、M24节点极限弯矩下降20%左右,M27节点极限弯矩下降50%左右.当螺纹啮合数减少1以上时,三种节点极限弯矩下降较大,均在50%左右.
| 表 6 螺栓球节点弯矩-转角曲线参数分析 Table 6 Analysis on moment-rotation curves of bolt-ball joints |
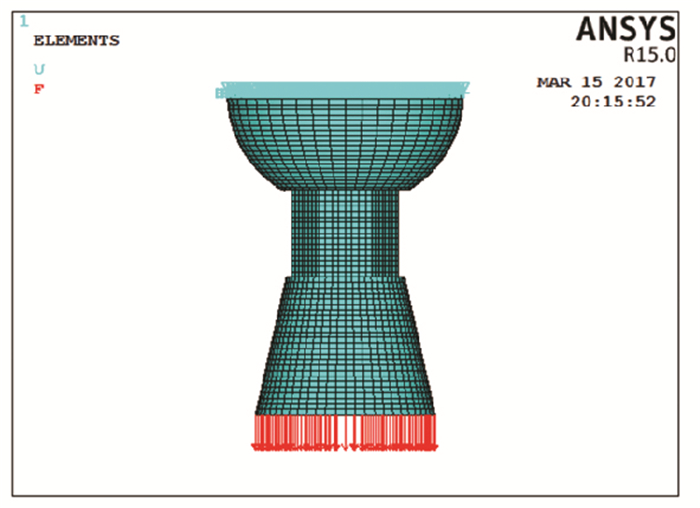
对于螺栓球节点来说,节点受压时主要靠套筒受力,高强螺栓不受力.节点受拉时主要靠高强螺栓与球体啮合部分受力,因此高强螺栓拧入长度不足会对节点抗拉性能产生较大影响[15].以下将对高强螺栓拧入长度不足时节点抗拉性能分析,分析模型见图 11.
|
图 11 有限元模型 Figure 11 Finite element model |
限于篇幅,本文以M20节点为例,通过分析发现,由于高强螺栓拧入长度的不同,螺栓球节点在拉力作用下存在两种工作及破坏模式.
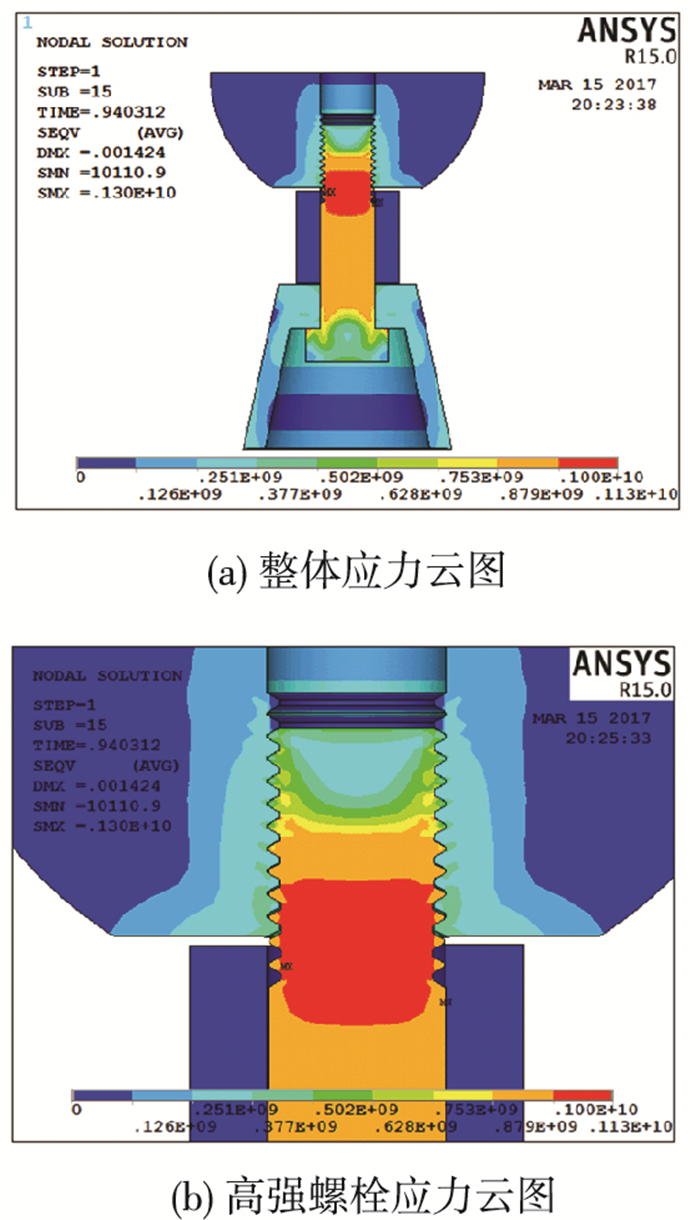
第一种为高强螺栓拧满或轻微不足时的栓杆拉断破坏,以M20-9节点为代表.图 12(a)、(b)为M20-9节点极限状态下的应力云图,可以看出,高强螺栓的栓杆区域完全进入极限状态,其他部分只有局部点应力较高,均未进入极限状态.节点破坏形式表现为高强螺栓的栓杆拉断破坏,为延性破坏,极限荷载为277.32 kN.
|
图 12 M20-9节点模拟云图 Figure 12 Simulated nephograms of M20-9 joint |
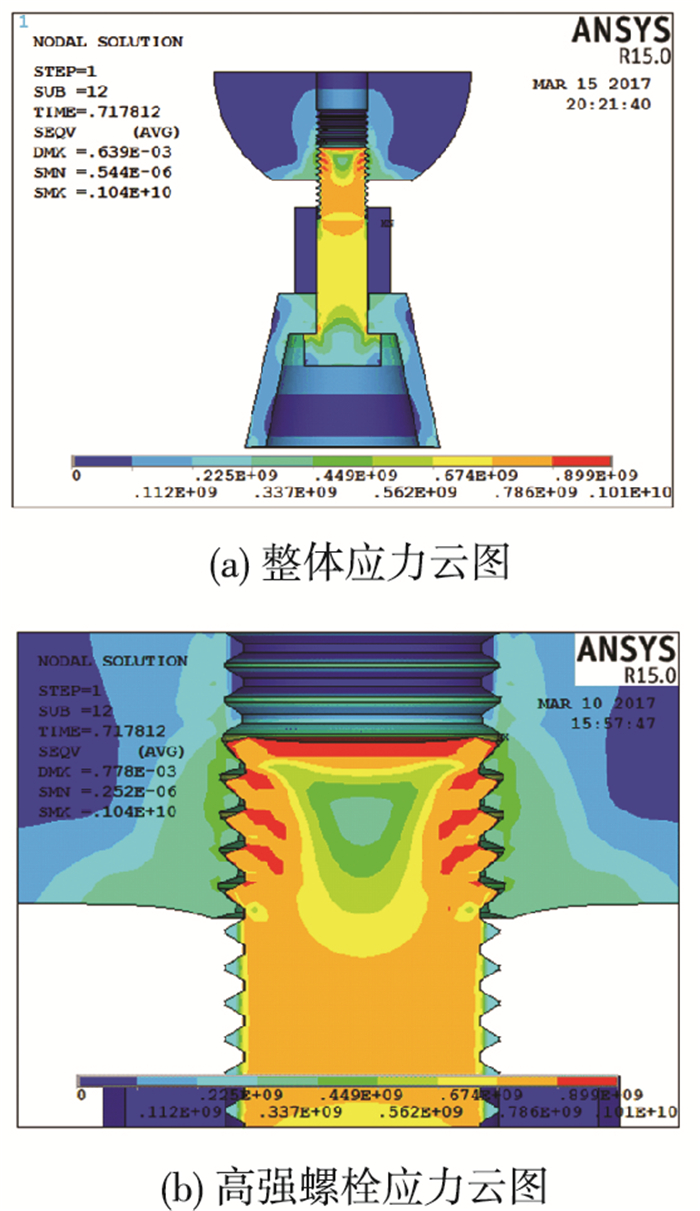
第二种为高强螺栓拧入长度严重不足时的栓杆拔出破坏,以M20-5节点为代表.图 13(a)、(b)为M20-5节点极限状态下的应力云图,可以看出,随着啮合数的减少,各螺纹受力提升较多,最大应力出现在高强螺栓螺纹部分,其余构件均未达到极限状态,这与文献[16-17]中规律相同.节点破坏形式为高强螺栓螺纹失效的栓杆拔出破坏,为脆性破坏,极限承载力降低明显,极限荷载为158.13 kN.
|
图 13 M20-5节点模拟云图 Figure 13 Simulated nephograms of M20-5 joint |
提取三种节点抗拉承载力见表 7,可知三种节点在螺纹啮合数减少的情况下承载力的发展规律相似,当螺纹啮合数减少1个时节点仍发生高强螺栓的栓杆拉断破坏.当螺纹啮合减少2个以上时节点发生高强螺栓螺纹失效的栓杆拔出破坏.
| 表 7 螺栓球节点抗拉承载力分析 Table 7 Analysis on tensile bearing capacity of bolt-ball joints |
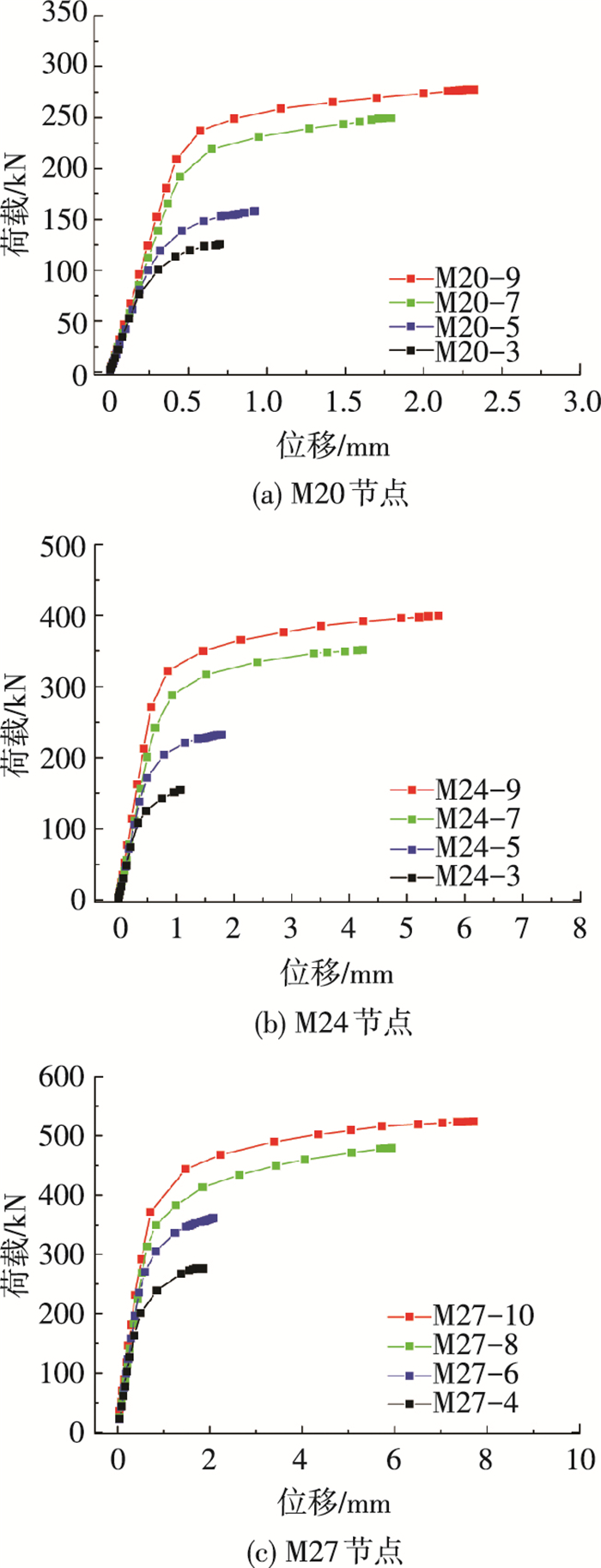
绘制荷载-位移曲线见图 14,随着高强螺栓拧入长度的减少,节点的极限荷载下降明显,节点由延性破坏变成螺纹失效的脆性破坏.施工中应严格控制高强螺栓拧入螺纹个数,避免脆性破坏的发生.
|
图 14 高强螺栓不同拧入长度下位移-荷载曲线 Figure 14 Displacement-load curves of high-strength bolts under different inserted depth |
为了更好描述螺栓球节点抗拉承载力随拧入比例的变化规律,采用线性拟合的方式对承载力与拧入比例进行数据处理,其拟合公式为
| $ y = ax + b. $ |
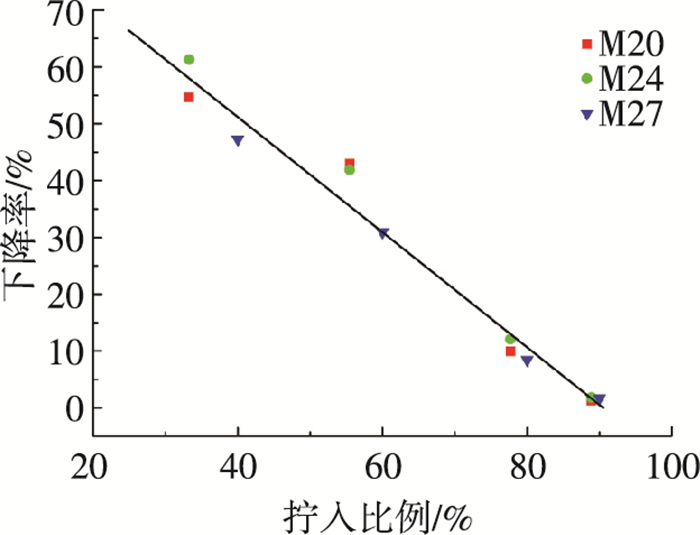
式中:y表示拧入长度不足时螺纹承载力与初始承载力的比值,%;x表示拧入比例,%;a、b为拟合常数.图 15为高强螺栓拧入比例与抗拉承载力之间的线性拟合图, 相关拟合公式的参数值a=-101.285, b=91.679.
|
图 15 高强螺栓拧入比例与抗拉承载力关系曲线 Figure 15 Relation curve of high-strength bolts' inserted proportion and tensile bearing capacity |
为掌握高强螺栓拧入长度不足对螺栓球节点受力性能的影响规律,本文对常用螺栓球节点不同拧入长度下的力学性能进行研究,得到如下结论:
1) 建立了带有螺纹的螺栓球节点精细化模型,并采用精细化模型对已有试验进行模拟分析.结果表明,本文模型可以真实的考虑高强螺栓和螺栓球之间的螺纹啮合传力,能够更好地模拟节点的受力性能,验证了模拟的准确性.
2) 通过模拟发现,随着高强螺栓拧入长度的改变,节点在弯矩作用下主要存在三种工作及破坏模式,与之对应的弯矩-转角曲线也存在三种状态.当螺纹啮合数减少1个时,M20、M24节点极限弯矩下降在20%左右,M27节点极限弯矩下降在50%左右,即螺纹啮合数减少1个时,M27节点承载力及刚度下降更加明显,其抗弯性能对拧入误差更为敏感;当螺纹啮合数减少1个以上时,三种节点极限弯矩下降较大,均在50%左右.高强螺栓拧入长度不足严重降低节点刚度及其极限承载力.
3) 对高强螺栓拧入长度不足下螺栓球节点受拉性能的分析表明,节点主要存在两种工作及破坏模式,当螺纹啮合数减少1个以内时,节点发生高强螺栓栓杆拉断的延性破坏;当螺纹啮合数减少1个以上时,节点发生螺纹失效的脆性破坏.最后,通过线性拟合给出了螺栓球节点抗拉承载力降低比例与高强螺栓拧入比例的关系曲线,可为螺栓球节点拧入长度不足下的承载力快速评估与施工控制提供参考.
| [1] |
杨璐, 王元清, 袁焕鑫, 等. 网架钢结构施工缺陷分析与处理[J].
四川建筑科学研究, 2014, 40(2): 341-344.
YANG Lu, WANG Yuanqing, YUAN Huanxin, et al. Analysis and treatment of construction defects of steel grid structure[J]. Sichuan Building Science, 2014, 40(2): 341-344. |
| [2] |
空间网格结构技术规程: JGJ7—2010[S]. 北京: 中国建筑工业出版社, 2010: 34-35.
Technical specification for space frame structures: JGJ—2010[S]. Beijing: China Architecture & Building Press, 2010:34-35. |
| [3] |
田昱峰, 冯霞. 导致网架事故的设计原因分析[J].
山西建筑, 2007, 33(25): 113-114.
TIAN Yufeng, FENG Xia. Study on the design factors caused the accidents of grid structure[J]. Shanxi Architecture, 2007, 33(25): 113-114. DOI: 10.3969/j.issn.1009-6825.2007.25.069 |
| [4] |
林健. 某螺栓球节点网架厂房坍塌事故分析[D]. 太原: 太原理工大学, 2016.
LIN Jian. The analysis of collapse accident on an industrial workshop with bolt-ball node grid[D]. Taiyuan:Taiyuan University of Technology, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10112-1016714337.htm |
| [5] |
SEE T. Large displacement elastic buckling space structures[D]. England: Cambridge of University, 1983.
|
| [6] |
FATHELBAB F A.The effect of joints on the stability of shallow single layer lattice domes[D]. England: University of Cambridge, 1987.
http://ethos.bl.uk/OrderDetails.do?uin=uk.bl.ethos.233896
|
| [7] |
张传成, 张宝勤, 张爱林. 节点刚度对2008奥运羽毛球热身馆单层网壳稳定性影响研究[J].
世界地震工程, 2007, 23(3): 32-40.
ZHANG Chuancheng, ZHANG Baoqin, ZHANG Ailin. Stability behavior of joint stiffness on the single-layer reticulated shell of badminton arena for 2008 Olympic Games[J]. World Earthquake Engineering, 2007, 23(3): 32-40. |
| [8] |
曹正罡, 陈哲明, 万宗帅, 等. 80 m球径螺栓球节点单层球面网壳稳定性能分析[J].
哈尔滨工业大学学报, 2015, 47(6): 1-8.
CAO Zhenggang, CHEN Zheming, WAN Zongshuai, et al. Analysis of stability of 80 m diameter single-layer reticulated dome with bolt-sphere joints[J]. Journal of Harbin Institute of Technology, 2015, 47(6): 1-8. |
| [9] |
CHENAGHLOU M R. Semi-rigidity of connections in space structures[J]. 1997.
|
| [10] |
钢网架螺栓球节点用高强度螺栓: GB/T 16939—2016[S]. 北京: 中国建筑工业出版社, 2016: 9-10.
High strength bolts for joints of space grid structures: GB/T 16939—2016[S]. Beijing: China Architecture & Building Press, 2016:9-10. |
| [11] |
普通螺纹基本尺寸: GB/T 196—2003[S]. 北京: 中国建筑工业出版社, 2003: 1-4.
General purpose metric screw threads-Basic dimensions:GB/T 196—2003[S]. Beijing: China Architecture & Building Press, 2003:1-4. |
| [12] |
范峰, 马会环, 沈世钊. 半刚性螺栓球节点受力性能理论与试验研究[J].
工程力学, 2009, 26(12): 92-99.
FAN Feng, MA Huihuan, SHEN Shizhao. Numerical simulation and experimental study on mechanical characters of ball-bolt joint system[J]. Engineering Mechanics, 2009, 26(12): 92-99. |
| [13] |
KATO S, MUTOH I, SHOMURA M. Collapse of semi-rigidly jointed reticulated domes with initial geometric imperfections[J].
Journal of Constructional Steel Research, 1998, 48(2): 145-168.
|
| [14] |
王燕, 李华军, 厉见芬. 半刚性梁柱节点连接的初始刚度和结构内力分析[J].
工程力学, 2003, 20(6): 65-69.
WANG Yan, LI Huajun, LI Jianfen. Initial stiffness of semi-rigid beam-to-column connections and structural internal force analysis[J]. Engineering Mechanics, 2003, 20(6): 65-69. |
| [15] |
黄炳生, 付宜东, 陈烨, 等. 螺栓球节点高强度螺栓拧入深度试验研究[J].
建筑钢结构进展, 2016, 18(4): 28-32.
HUANG Bingsheng, FU Yidong, CHEN Ye, et al. Experimental study on the depth of high strength bolt into bolt-sphere joint[J]. Progress in Steel Building Structures, 2016, 18(4): 28-32. |
| [16] |
ZHAO H. A Numerical Method for Load Distribution in Threaded Connections[J].
Journal of Mechanical Design, 1996, 118(2): 274.
DOI: 10.1115/1.2826880 |
| [17] |
陈海平, 曾攀, 方刚, 等. 螺纹副承载的分布规律[J].
机械工程学报, 2010, 46(9): 171-178.
CHEN Haiping, ZENG Pan, FANG Gang, et al. Load distribution of bolted joint[J]. Journal of Mechanical Engineering, 2010, 46(9): 171-178. |
 2017, Vol. 49
2017, Vol. 49


