随着时代的发展,中国的建筑趋于高层、超高层建筑.近年来,中国超高层建筑发展迅速,超高层建筑的竖向构件较多采用钢管混凝土组合结构,钢管混凝土具有承载力高、延性好、耐火性好以及施工简便等优点,应用广泛.随着建筑样式的多样化,有时为满足建筑的需要,会产生异形截面巨型钢管混凝土柱.同时为满足抗震性能要求,异形截面巨型钢管混凝土柱内部被钢板分隔成若干腔体,形成巨型多腔体钢管混凝土柱.天津117大厦,大连国贸中心,北京中国尊等超高层建筑,均采用了异形截面多腔钢管混凝土柱.
目前,对异形截面多腔钢管混凝土柱抗震性能的研究较为欠缺.曹万林等[1-3]对异形截面多腔钢管混凝土柱进行了抗震性能研究,提出了相关构造措施的建议,研究成果表明多腔钢管混凝土柱与单腔钢管混凝土柱相比,具有较好的抗震性能;钢管混凝土的截面构造及钢筋笼的设置对钢管混凝土柱的承载力和延性有较大的影响.张建伟等[4]研究了不同构造措施对八边形截面多腔钢管混凝土柱抗震性能的影响,研究结果表明设置分腔板,竖向肋板及角钢能够显著提高其抗震性能.王丹等[5]进行了T、L形截面钢管混凝土柱的抗震性能试验,研究表明轴压比、钢管壁厚和混凝土强度对承载力有较大影响.林震宇等[6]对L形钢管混凝土柱的抗震性能试验表明设置加劲肋可以提高钢管混凝土柱的延性,且可以延缓钢板的屈曲.荣斌等[7]进行了L形截面方钢管混凝土组合柱受压性能相关研究,并提出了相关计算公式.以上文献对多腔钢管混凝土结构进行了研究,但缺乏对不同腔体具有不同高度时的性能研究,如分叉柱等情况.
为满足上述要求,本文以北京某在建超高层建筑为工程背景,在课题组已完成的异形截面多腔钢管混凝土分叉柱抗震性能试验研究的基础上[8],进行了有限元分析和参数研究,对比分析了不同构造措施、不同钢材及混凝土强度等级等参数对分叉柱抗震性能的影响,为相关工程提供理论依据和设计参考.
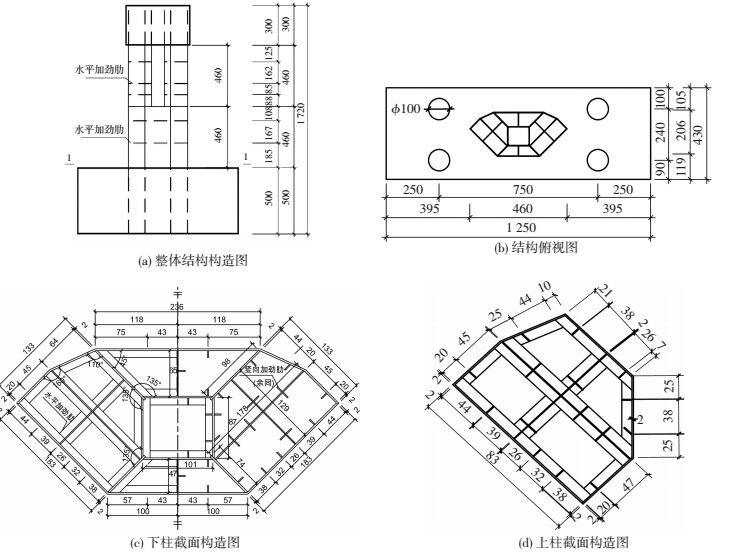
1 试验概况以北京某在建超高层建筑异形截面多腔体钢管混凝土分叉柱为工程参考模型[8],设计了4个1/30尺寸试验模型,如图 1所示.模型编号分别为CFTC1-X、CFTC2-X、CFTC1-Y、CFTC2-Y.“1、2”分别代表钢管厚度为2 mm和3 mm,“X、Y”分别代表钢管混凝土柱沿长轴方向加载、沿短轴方向加载.试件高920 mm,距基础顶面高460 mm处分叉为两根柱,试件的加劲肋横截面尺寸为5 mm×2 mm.模型设计见图 1.模型设计参数及材料力学性能见表 1.
|
图 1 试件模型几何尺寸及构造[8](mm) Figure 1 Details and dimensions of specimens (mm) |
| 表 1 模型设计参数 Table 1 Design parameters of specimens |
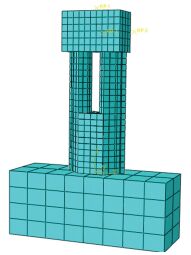
本文采用有限元分析软件ABAQUS进行有限元分析.为准确描述实际构件,模型建立采用全模型的方法.为反应实际构造的特点,钢管混凝土柱的模型中,钢管部分采用三维可变形壳单元,混凝土部分采用三维可变形实体单元,隔板采用三维可变形实体单元,模型示意见图 2.
|
图 2 有限元分析模型 Figure 2 Finite element model |
混凝土采用ABAQUS软件中提供的损伤塑性模型(damaged plasticity), 确定钢材与核心混凝土的应力-应变关系模型,进行钢管混凝土构件的荷载-变形关系曲线全过程分析.核心混凝土本构采用方、矩形钢管混凝土柱考虑约束效应的应力-应变关系表达式[9],并参考文献[10]中的理论分析方法,计算得到分腔钢板、水平隔板和纵向加劲肋的贡献,提高混凝土的峰值强度及峰值应变,修正文献[9]给出的应力-应变关系曲线,从而得到适用于ABAQUS有限元模拟的异形截面多腔钢管约束混凝土本构关系,泊松比取0.2.混凝土参数取值见表 2[11],表中Fb0/fc0为双轴等抗压强度和单轴抗压强度的比值,K为常数,是拉、压子午线上第二应力不变量的比值.
| 表 2 混凝土有限元计算模型参数取值 Table 2 Parameters of concrete finite element models |
钢材采用Q345钢,钢材本构曲线采用三折线模型,为更好模拟钢材实际应力-应变关系[9], 钢材屈服强度、钢材极限强度取实测值,泊松比取0.3.
2.3 界面模拟与荷载施加模型外钢板采用整体建模,分叉面上下分别建模后合并成为一个整体壳结构.钢板与混凝土界面接触采用表面与表面接触(Standard),其中钢板表面为主表面,混凝土表面为从表面,滑移公式为有限滑移.为确保主表面与从表面精确接触,从节点/表面调整选为“只为调整为删除过盈”.接触作用属性中,切向行为摩擦公式采用罚函数,摩擦系数取0.4,法向行为采用硬接触.钢管内部钢板嵌入(embedded)到混凝土中.肋板与钢板绑定,且嵌入混凝土中.
基础底部为固定端,底面设置为完全固定,加载端为自由端.水平荷载采用一次加载,增加2个分析步,第一步施加竖向轴力,轴力大小为900 kN,第二步在加载端施加位移荷载.多、高层结构弹塑性层间位移角限值为1/50[12],为更好模拟钢管混凝土模型破坏以及承载力下降,本文采用1/30弹塑性层间位移角,加载幅值为软件默认值.
2.4 单元的选取与网格划分为更好模拟实际情况,简化计算,钢管部分采用S4R单元[13],网格采用四边形自由化网格划分;肋板部分与混凝土采用C3D8R单元,网格采用六面体结构网格划分,其余部分按软件默认值选择.
按以上步骤建立试件的有限元模型,计算并得出有限元模型的水平荷载F与水平位移U的F-U关系曲线,并与试验得出的F-U关系曲线进行对比,从而验证有限元模拟的合理性与可信性.
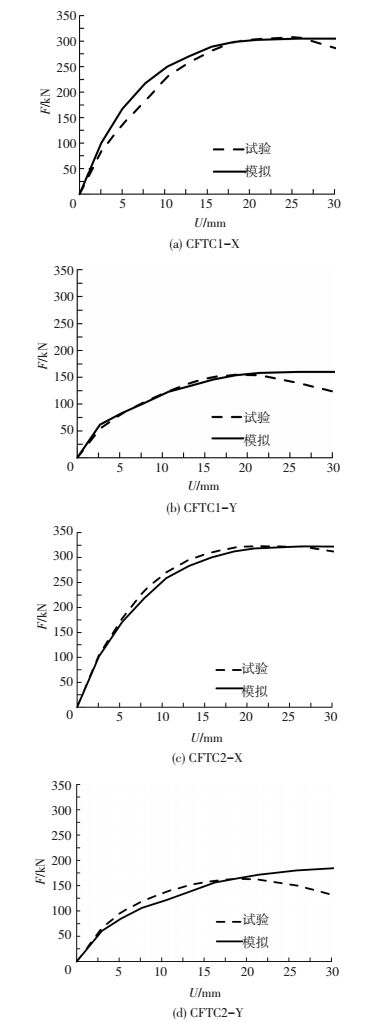
2.5 有限元计算结果根据有限元分析结果,其F-U曲线与试验的正向F-U曲线对比见图 3.
|
图 3 F-U曲线对比 Figure 3 Comparison of F-U curves |
试验得出的正向钢管混凝土分叉柱的骨架曲线与有限元分析得到的钢骨架曲线吻合良好,在试件加载初期,二者刚度基本一致;随着位移增大,试件开裂损伤,曲线开始出现偏移但总体较为吻合.试验得到的峰值荷载在同位移下的有限元分析得到的荷载比值为1.009,有限元分析结果能准确模拟试验结果.
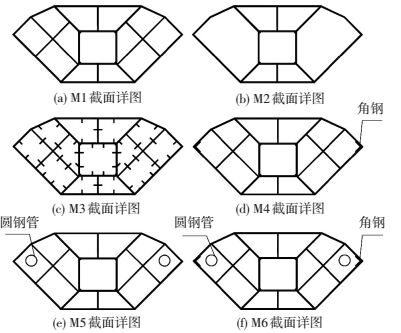
3 参数研究 3.1 不同构造措施对钢管混凝土力学性能的影响 3.1.1 模型设计在试验模型基础上,设计6个有限元分析模型.其不同点在于腔体数量、竖向肋板、角部加角钢、边缘腔体内加钢管等构造措施.模型编号为M1、M2、M3、M4、M5、M6.其中M1为无纵向肋板的13腔体试件,钢板厚2 mm;M2为八边形7腔体试件,钢板厚3 mm,M2与M1用钢量相同;M3为加纵向肋板13腔体试件,钢板厚2 mm;M4为无纵向肋板13腔体试件,设置角钢,除角钢外板厚2 mm,角钢为40 mm×3 mm×920 mm(肢长×厚度×高度);M5为无肋板13腔体,角部腔体内置直径30 mm钢管,钢板和钢管厚为2 mm;M6为加纵向肋板和直径30 mm钢管.模型设计图见图 4,模型设计参数及材料见表 3.
|
图 4 模型截面设计图 Figure 4 Cross section of models |
| 表 3 模型设计参数 Table 3 Parameters of model design |
为更好模拟实际情况并简化计算,钢管部分采用S4R单元,网格采用四边形自由化网格划分;肋板部分与混凝土采用C3D8R单元,网格采用六面体结构网格划分, 其余部分按软件默认值选择.
3.1.3 计算结果1) 不同构造措施对钢管混凝土柱力学性能影响
图 5为模型的F-U曲线,可以看出,M6、M3、M4、M5、M1、M2水平承载力依次降低.M2、M5、M1、M4后期承载力略有下降,其中,M2下降最为明显.这是由于试件M2为7腔体试件,截面构造措施较弱,延性较差,出现了较为明显的下降段.表 4为水平极限荷载计算值.其中Fy为屈服承载力,Fu为极限承载力;Δy为与屈服承载力相对应的极限位移,Δu为与极限承载力相对应的极限位移;μ为延性系数(=Δu/Δy).屈服点为按面积等效法确定.
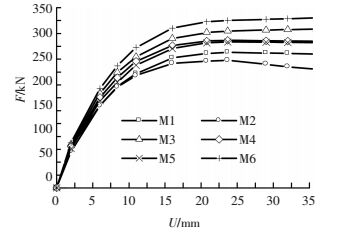
|
图 5 不同构造措施下水平荷载-位移曲线 Figure 5 Curve of F-U with different constructions |
| 表 4 模型水平极限承载力值 Table 4 Ultimate loads of models |
M2与M1相比,极限承载力降低7%,延性降低10%,在等用钢量下,增加腔体数量比增加钢板厚度能更有效地提高分叉柱的抗震性能.分腔钢板可以降低外部钢管的宽厚比,延缓屈曲并提高承载力.
M3与M1相比,极限承载力提高17%,延性提高了18%.表明竖向加劲肋的增设,能有效提高其抗震性能,竖向加劲肋可有效延缓钢板屈曲,提高钢板对混凝土的约束作用,增强混凝土与管壁的拉结性能,加强钢管和混凝土整体性.
M4、M5与M1相比,极限承载力分别提高9%、7%,延性分别提高8%、10%.表明增设角钢或钢管能一定程度提高承载力和延性.M6比M1极限承载力提高25%,且M6提高百分比大致等于M3和M5之和.
2) 应力变化分析
图 6为达到极限承载力时钢材的Mises应力云图.由图可知,当达到极限承载力时,6个模型柱脚钢管受压和受拉屈服(屈服压强为345 MPa),且受压屈服范围明显大于受拉屈服范围,屈服区域由柱底逐渐向上延伸,分叉面处屈服区由分叉处向上下两个方向延伸.M1分腔板屈服范围略低于外部钢管,说明内部分腔板可以延缓钢板屈曲,M2由于分腔少,外部钢管屈曲面积较大;M3纵向肋板与外部钢管屈曲范围相近,但纵向肋板屈曲范围略少于外部钢管,表明纵向肋板能延缓钢管屈曲.M4、M5角钢和钢管屈服范围大致与外部钢管相同,表明添加角钢和钢管能够有效提高柱的承载能力.
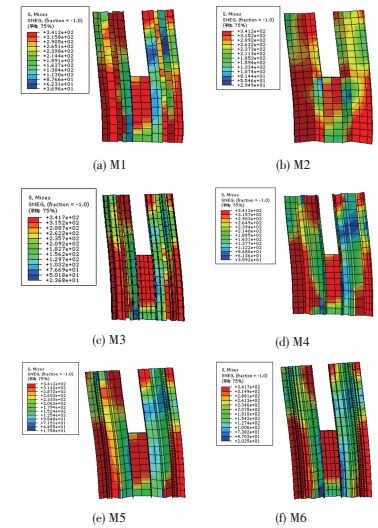
|
图 6 不同构造下钢管Mises应力云图 Figure 6 Mises stress of steel tubes with different construction |
由图 7可知,在极限承载力下,M2中混凝土分担承载力较大,M6中最小;表明在添加肋板和钢管后,钢管混凝土整体性有所提高.分叉柱的截面应力图可以看出,M2受拉区域最小,在增加分腔板、纵向肋板、角钢之后,混凝土受拉面积增加,承载力有所提高.
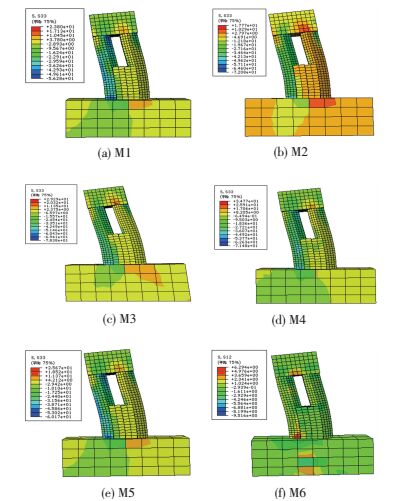
|
图 7 不同构造下混凝土S33应力云图 Figure 7 S33 stress of construction with different construction |
综上所述,钢管混凝土柱在设置纵向肋板,角钢和钢管后,其水平承载力会有所提高,在同时设置纵向肋板和钢管、角钢后,水平极限承载力提高幅度大致为单个构造设置之和.
3.2 不同材料强度等级模型分析 3.2.1 模型设计以试验试件为原型,为研究不同强度材料对该截面形式的多腔钢管混凝土巨型分叉柱的力学性能的影响,坚持模型设计与实际试验相匹配原则,设计6个有限元模型.钢材强度分为Q235、Q345、Q390、Q420.混凝土强度分为C30、C40、C50.钢材强度设计值按照国家标准GB 50017—2003《钢结构设计规范》选取.混凝土本构模型与钢材本构模型根据文献[9]选取.
模型分别编号为H1、H2、H3、H4、H5、H6.其中H1使用Q235钢材, H2为Q345钢材, H3为Q390钢材, H4使用Q420钢材, H5使用C30混凝土, H6使用C50混凝土.模型设计参数见表 5.
| 表 5 模型设计参数 Table 5 Parameters of model design |
图 8为模型的F-U曲线.H4、H3、H2、H1水平承载力依次降低.表 6为模型水平极限承载力计算值.其中Fu为模型极限承载力, Δu为与水平力相对应的极限位移.
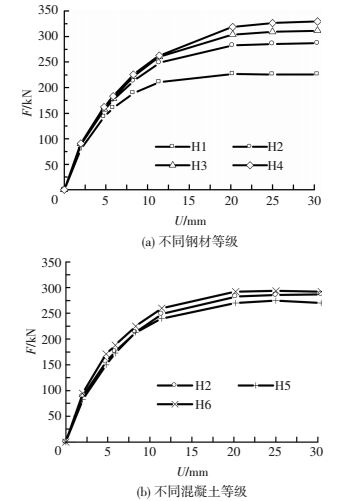
|
图 8 不同材料强度等级模型F-U曲线 Figure 8 F-U curves with different materials |
| 表 6 水平极限承载力 Table 6 Ultimate loads of models |
由表 6可以看出,H2比H1极限承载力提高21%;H3比H2极限承载力提高8%;H4比H3极限承载力提高7%;H5比H2极限承载力降低1%;H6比H2极限承载力提高1%.由图 8可以看出,在水平位移小于10 mm时,H1刚度最小,H2、H3、H4刚度大致相同;达到极限位移后,钢材从Q235提高到Q345的承载力提高幅度最大,当钢材强度再次提高时,极限承载力提高幅度相对较小.可以得出:当混凝土等级为C40时,Q345相对其他钢材而言,性价比最高.当混凝土等级提高时,钢管混凝土柱的承载力和刚度略有提高.同时,混凝土与钢材的不同等级的组合,对后期承载力的下降段即延性有一定影响,设计中需充分考虑混凝土与钢材的强度匹配.
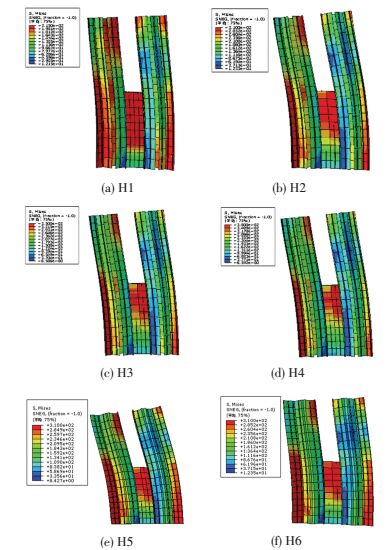
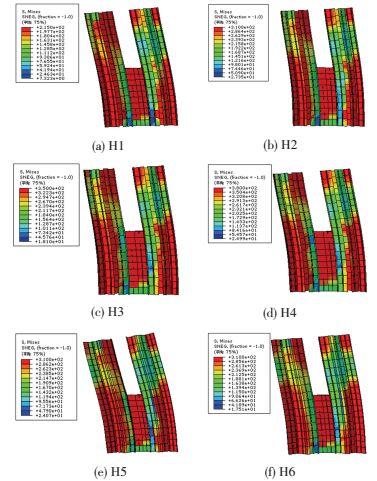
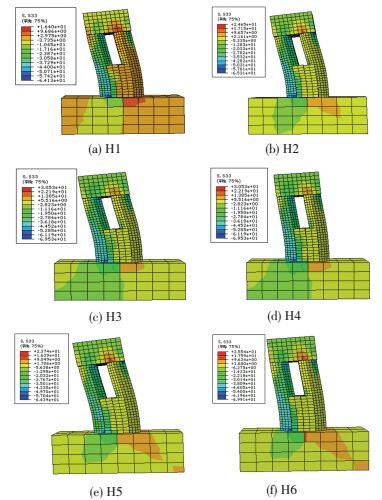
3.2.3 应力分析图 9为位移角为1/100时钢管Mises应力云图.图 10、11为位移角为极限荷载时的应力云图.
|
图 9 位移角为1/100钢管应力Mises云图 Figure 9 Mises stress of steel tube at 1/100 drift ratio |
|
图 10 钢管应力Mises云图 Figure 10 Mises stress nephogram of steel tube |
|
图 11 混凝土沿纵向应力(S33)分布图 Figure 11 S33 stress nephogram of concrete along longitude |
由图 9可知,位移角为1/100时,H1钢管的屈服区域较大,其次为H2,H3、H4屈服区域相近.结合图 10可以看出,此时H1接近极限承载力状态,其他结构承载力仍处于上升段.
由图 10、11可以看出,在达到极限承载力时钢管屈服应力较为接近,混凝土的纵向应力H1明显小于H2、H3、H4,且H3、H4之间应力范围变化不大.在分叉面,当钢管强度等级提高时,混凝土截面受拉区域随着钢管强度等级提高有小幅度的增加.
4 结论1) 基于本文提出的有限元建模方法,所得有限元分析结果与试验结果吻合较好.
2) 适当增加腔体数,设置肋板、角钢和钢管,能够有效提高异形截面钢管混凝土分叉柱抗震性能.
3) 在等用钢量下,增加腔体数量比增加钢板厚度能更有效地提高分叉柱抗震性能.
4) 不同材料强度对异形截面钢管混凝土分叉柱抗震性能有较大影响,在进行其抗震设计时,宜选用强度等级匹配的钢材与混凝土.
| [1] |
曹万林, 彭斌, 王智慧, 等. 底部加强型多腔钢管混凝土巨型柱抗震性能试验研究[J].
地震工程与工程振动, 2012, 32(2): 120-129.
CAO Wanlin, PENG Bin, WANG Zhihui, et al. Experimental research on seismic behavior of bottom strengthened multi-cell CFST mega-columns[J]. Earthquake Engineering & Engineering Dynamics, 2012, 32(2): 120-129. DOI: 10.13197/j.eeev.2012.02.020 |
| [2] |
彭斌, 曹万林, 王智慧, 等. 多腔钢管混凝土柱巨型框架抗震性能试验研究[J].
结构工程师, 2012, 28(3): 128-234.
PENG Bin, CAO Wanlin, WANG Zhihui, et al. Experimental research on seismic behavior of Mega-Frame with Multi-Cell CFST columns[J]. Structural Engineers, 2012, 28(3): 128-234. DOI: 10.15935/j.cnki.jggcs.2012.03.020 |
| [3] |
曹万林, 武海鹏, 王立长, 等. 不同加载方向下五边形截面钢管混凝土巨型柱抗震性能试验研究[J].
建筑结构学报, 2014, 35(1): 69-76.
CAO Wanlin, WU Haipeng, WANG Lichang, et al. Seismic behavior of pentagonal cross-section CFST mega-columns under horizontal loading in different directions[J]. Journal of Building Structures, 2014, 35(1): 69-76. DOI: 10.14006/j.jzjgxb.2014.01.010 |
| [4] |
张建伟, 胡建华, 乔崎云, 等. 不同构造措施对异形截面多腔体钢管混凝土柱的力学性能影响[J].
北京工业大学学报, 2015, 41(8): 1172-1178.
ZHANG Jianwei, HU Jianhua, QIAO Qiyun, et al. Mechanical properties of special-shaped multi-cell CFST columns with different construction measures[J]. Beijing Gongye Daxue Xuebao, 2015, 41(8): 1172-1178. DOI: 10.11936/bjutxb2015010048 |
| [5] |
王丹, 吕西林. T形?L形钢管混凝土柱抗震性能试验研究[J].
建筑结构学报, 2005, 26(4): 39-44, 106.
WANG Dan, Lu Xilin. Experimental study on seismic behavior of concrete-filled steel T-section and L-section columns[J]. Journal of Building Structures, 2005, 26(4): 39-44, 106. DOI: 10.14006/j.jzjgxb.2005.04.006 |
| [6] |
林震宇, 沈祖炎, 罗金辉. 反复荷载作用下L形钢管混凝土柱滞回性能研究[J].
建筑钢结构进展, 2009(2): 12-17.
LIN Zhenyu, SHEN Zuyan, LUO Jinhui. Hysteretic behavior of concrete-filled L-section steel tubular columns under cyclic loading[J]. Progress in Steel Building Structures, 2009(2): 12-17. |
| [7] |
荣彬. 方钢管混凝土柱和L形截面方钢管混凝土组合异形柱研究[D]. 天津: 天津大学, 2005.
RONG Bin.Study on concrete-filled square steel tubular column and L-shaped column composed of concrete-filled square steel tubes[D]. Tianjin: Tianjin University, 2005. https://max.book118.com/html/2017/0704/120298734.shtm |
| [8] |
乔崎云, 李翔宇, 曹万林, 等. 异型截面多腔钢管混凝土分叉柱抗震性能试验研究[J].
地震工程与工程振动, 2016(2): 1-8.
QIAO Qiyun, LI Xiangyu, CAO Wanlin, et al. Study on seismic behavior of complex cross-section multi-cell CFST bifurcated-columns[J]. Earthquake Engineering & Engineering Dynamics, 2016(2): 1-8. DOI: 10.13197/j.eeev.2016.02.1.qiaoqy.001 |
| [9] |
韩林海.
钢管混凝土结构—理论与实践[M]. 第2版. 北京: 科学出版社, 2007: 73-83.
HAN Linhai. Steel Pipe Concrete Structure-Theory and Practice[M]. 2nd ed. Beijing: Science Press, 2007: 73-83. |
| [10] |
武海鹏. 异形截面多腔钢管混凝土柱受力性能试验与理论研究[D]. 北京: 北京工业大学, 2017.
WU Haipeng. Experimental and theoretical investigation on special-shaped CFT columns coupled with multiple cavities[D]. Beijing:Beijing University of Technology, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10005-1012036951.htm |
| [11] |
雷拓, 钱江, 刘成清. 混凝土损伤塑性模型应用研究[J].
结构工程师, 2008(2): 22-27.
LEI Tuo, QIAN Jiang, LIU Chengqing. Application of damaged plasticity model for concrete[J]. Structural Engineers, 2008(2): 22-27. DOI: 10.15935/j.cnki.jggcs.2008.02.010 |
| [12] |
钢结构设计规范: GB 50017—2003 [S]. 北京: 中国建筑工业出版社, 2003.
Code for design of steel structures: GB 50017—2003[S].Beijing:China Architecture & Building Press, 2003. |
| [13] |
郭兰慧, 戎芹, 张素梅. 方钢管混凝土中钢管屈曲承载力研究[J].
哈尔滨工业大学学报, 2011, 43(10): 6-11.
GUO Huilan, RONG Qin, ZHANG Sumei. Study on flexural capacity of steel tube in concrete-filled square steel tube[J]. Journal of Harbin Institute of Technology, 2011, 43(10): 6-11. DOI: 10.11918/j.issn.0367-6234.2011.10.002 |
 2017, Vol. 49
2017, Vol. 49


