2. 同济大学 地下建筑与工程系,上海 200092
2. Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China
楔形桩是一种实用高效的桩形.工程实践及现场试验表明[1],楔形桩型具有承载力大而沉降小的特点.然而,目前楔形单桩和群桩在设计使用时,尚无对应的规范和有效计算方法,这在一定程度上限制了其进一步的推广使用.
国内外学者对单桩的承载性能进行了许多研究:Randolph等[1]假定桩的侧阻与沉降为线性关系,根据剪切位移法提出了均匀土体中单桩和群桩的荷载-沉降计算方法;Norlund[2]和Robinsky等[3]分别利用现场试验和室内试验研究了楔形桩的承载性能,发现楔形摩擦桩比等截面桩承载力更大;陈龙珠等[4]用线弹性-硬化模型表示桩-土相互关系,提出了桩基荷载-沉降曲线的解析算法;Kraft等[5]根据桩侧土体剪应力与剪应变之间的双曲线关系导出了割线剪切模量的表达式; 刘杰等[6]假定楔形桩的桩-土间荷载-沉降关系满足双曲线模型,得到了计算楔形桩荷载-沉降曲线的方法,但其计算参数需要大量现场试桩确定.
在相同荷载作用下,群桩沉降往往比单桩更大,一般将这种桩体之间相互作用引起的效果称为“群桩效应”.Randolph等[7]基于迭代方法提出了考虑群桩沉降相互作用的群桩沉降计算方法;Mylonakis等[8]基于剪切位移法提出了分层土中群桩沉降问题的简便计算方法;Zhang等[9]假定桩侧与桩端土体分别满足双曲线和双折线荷载传递模型,得到了单桩的荷载-沉桩曲线,并在此基础上利用影响系数提出了群桩的荷载-沉降曲线的计算方法;刘杰等[10-11]利用模型试验和理论推导的方法研究了夯实水泥土楔形桩复合地基中群桩的沉降、最佳楔形角以及荷载传递等问题; Lee[12]利用双曲线模型研究了分层土中群桩的沉降问题.
上述研究大多数集中于等截面桩的荷载-沉降关系,对楔形桩的荷载-沉降关系研究较少.此外,国内尚无关于楔形单桩及群桩的规范说明.基于此,本文假定楔形桩桩侧和桩端土体分别满足双曲线和双折线荷载传递模型,得到了楔形单桩荷载沉降曲线计算方法;利用有限差分法求解了楔形桩相互作用的控制微分方程,提出了楔形群桩的荷载-沉降计算方法,并通过与现有试验结果进行对比验证了本文计算方法的有效性.本文提出的楔形单桩及群桩沉降计算方法可以较为合理地预测楔形单桩和群桩在轴向荷载作用下的沉降曲线,具有一定理论与实际意义.
1 楔形单桩荷载-沉降解析 1.1 基本假定1) 桩体为理想圆台体,在同一土层内,桩-土界面参数不变,受荷过程中,桩始终处于弹性变形阶段;
2) 土体为分层土,同一土层内,土的性质均匀;
3) 桩侧土的应力-沉降满足双曲线关系,桩端土的应力-沉降满足双折线关系.
1.2 楔形桩桩侧双曲线型荷载传递模型楔形桩承受竖向荷载时,单位长度桩提供的承载力与其沉降呈现出典型的非线性关系.这其中:双曲线模型既能很好地模拟桩体沿桩长方向承载能力发挥过程,又有参数简单、物理意义明确等特点,故许多学者[5-6, 9]在研究桩-土相互作用时都采用双曲线模型.本文采用双曲线型桩侧荷载传递模型模拟楔形桩桩侧的荷载-沉降关系.如图 1所示,其表达式为

|
图 1 桩侧应力-沉降双曲线模型 Figure 1 Hyperbolic nonlinear relationship between shear stress and settlement at the pile-soil interface |
| $ {\tau _{\rm{s}}}\left( z \right) = \frac{{S\left( z \right)}}{{a + bS\left( z \right)}}. $ | (1) |
式中:τs(z)为z深度处楔形桩桩-土界面的剪应力,S(z)为z深度处桩截面沉降.
由图 1可知,参数a的倒数1/a代表了桩体的初始剪切刚度.由Randolph等[7]提出的桩侧刚度公式为
| $ a\left( z \right) = \frac{{{r_0}\left( z \right)}}{{{G_{\rm{s}}}}}\ln \left[ {\frac{{{r_{\rm{m}}}\left( z \right)}}{{{r_0}\left( z \right)}}} \right]. $ | (2) |
式中:r0(z)为深度z处的桩半径;rm(z)为深度z处桩沉降引起周围土体沉降的影响范围(受影响土体到桩中心的最大水平距离);Gs为土体剪切模量.
分层土中桩的沉降影响范围rm可用式(3)计算[12]:
| $ {r_{\rm{m}}} = 2.5L{\rho _{\rm{m}}}\left( {1 - {\upsilon _{\rm{m}}}} \right). $ | (3) |
ρm为修正系数,其表达式为
| $ {\rho _{\rm{m}}} = \frac{{\sum\limits_{k = 1}^{{m_{\rm{s}}}} {{G_{{\rm{s}}k}}{L_k}} }}{{{G_{{\rm{sm}}}}L}}. $ | (4) |
式中:υm为桩周土的平均泊松比,L为桩长,ms为桩范围内土的层数,Lk为第k层土中桩的长度,Gsk为第k层土的初始剪切模量,Gsm为桩范围内土的最大初始模量.
由图 1可知,参数b的倒数1/b表示桩侧极限阻力τsu.参数b与楔形桩楔形角,土体重度等有关.假设土在破坏时服从摩尔-库伦准则,利用极限状态理论可求得τsu.具体过程如下:
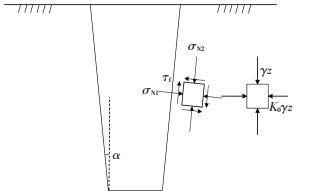
桩顶无荷载时:桩周土体应力状态如图 2右应力状态所示,由于桩-土界面和竖直方向存在一个楔形角,应力旋转之后,桩-土界面上的初始应力为
|
图 2 楔形桩力学计算模型 Figure 2 Mechanical model for the tapered pile |
| $ \left\{ \begin{array}{l} {\sigma _{{\rm{N1}}}} = {\sigma _z}{\sin ^2}\alpha + {\sigma _r}{\cos ^2}\alpha = \gamma z\left( {{{\sin }^2}\alpha + {K_0}{{\cos }^2}\alpha } \right),\\ {\sigma _{{\rm{N2}}}} = {\sigma _r}{\sin ^2}\alpha + {\sigma _z}{\cos ^2}\alpha = \gamma z\left( {{K_0}{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right). \end{array} \right. $ | (5) |
式中:γ为土重度,K0为静止土压力系数,α为楔形角.
极限状态下:外加荷载会同时引起桩-土接触面上正应力和剪应力增大.桩、土相互挤压过程中,垂直于桩-土界面方向的正应力(σN2)变化可以忽略不计.将各项应力代入Mohr-Coulomb屈服方程:
| $ \left( {\frac{{{\sigma _1} + {\sigma _3}}}{2} + c\cot \varphi } \right)\sin \varphi = \frac{{{\sigma _1} - {\sigma _3}}}{2}. $ | (6) |
式中:
桩-土界面正应力、剪应力在竖直方向投影可以得到楔形桩的极限侧阻应力为
| $ {\tau _{{\rm{su}}}} = {{\sigma '}_{{\rm{N1}}}}\left( {\tan \alpha + f} \right). $ | (7) |
联立式(5)、(6)、(7)可得
| $ \begin{array}{*{20}{c}} {{\tau _{{\rm{su}}}} = \gamma z\left( {{K_0}{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right)\left( {\tan \alpha + f} \right) \times }\\ {\frac{{1 + {{\sin }^2}\varphi + 2\sqrt {{{\sin }^2}\varphi - {f^2}{{\cos }^2}\varphi } }}{{4{f^2} + {{\cos }^2}\varphi }}.} \end{array} $ | (8) |
式中:f为桩-土界面摩擦系数,可通过拉拔试验或现场试验数据反演确定[13];φ为桩周土的内摩擦角.
进而,由式(8)可得
| $ b = \frac{1}{{{\tau _{{\rm{su}}}}}}. $ | (9) |
假设桩端土体应力-沉降关系满足双折线模型,如图 3所示.桩端应力τb与桩端沉降之间的关系为

|
图 3 桩端应力-沉降双线模型 Figure 3 Bilinear hardening relationship between shear stress and settlement at the pile tip |
| $ {\tau _{\rm{b}}} = \left\{ {\begin{array}{*{20}{c}} {{k_1}{S_{\rm{b}}},}&{{S_{\rm{b}}} \le {S_{{\rm{bu}}}};}\\ {{k_1}{S_{{\rm{bu}}}} + {k_2}\left( {{S_{\rm{b}}} - {S_{{\rm{bu}}}}} \right),}&{{S_{\rm{b}}} > {S_{{\rm{bu}}}}.} \end{array}} \right. $ | (10) |
式中:k1为桩端初始刚度,k2为桩端硬化阶段的刚度,Sbu为桩端开始硬化时的沉降.
假定桩端为半无限体上的刚性圆盘,则k1为[7]
| $ {k_1} = \frac{{4{G_{{\rm{sb}}}}}}{{{\rm{ \mathsf{ π} }}r\omega \left( {1 - {\upsilon _{\rm{b}}}} \right)}}. $ | (11) |
式中:Gsb为桩端土剪切模量;υb为桩端土的泊松比;r为桩端半径;ω为考虑桩形状与埋深的修正系数.
根据桩端硬化阶段的荷载-沉降关系,k2[9]为
| $ {k_2} = \frac{{\Delta {P_{\rm{t}}}}}{{{A_{\rm{p}}}\left( {\Delta {W_{\rm{t}}} - \frac{{\Delta {P_{\rm{t}}}L}}{{{E_{\rm{p}}}{A_{\rm{p}}}}}} \right)}} = \frac{{{k_{\rm{t}}}}}{{\left( {1 - {k_{\rm{t}}}\frac{L}{{{E_{\rm{p}}}{A_{\rm{p}}}}}} \right){A_{\rm{p}}}}}. $ | (12) |
式中:Ep为桩弹性模量;Ap为桩端面积;kt=ΔPt/ΔWt,即荷载-沉降曲线末段渐近线斜率;Sbu取值和土层性质、土层状态、桩体类型等等因素相关,在实际应用中,可先将试桩结果绘制成桩端沉降-应力关系图,采用双折线拟合反演求出Sbu,利用式(12)计算k2.
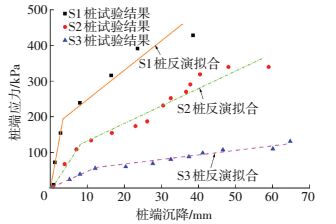
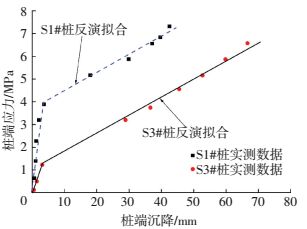
文献[14-15]对桩端承载问题进行过研究,砂土[14]和软土[15]中典型试桩归一化结果与本文反演结果对比见图 4、5.文献[14-15]中的反演结果见表 1;由表 1知Sbu变化范围较大,但在类似土层条件下[15],Sbu、k2反演结果十分接近,因此工程中可以利用类似工程数据进行推算.从图 4、5拟合结果可以看出利用双折线模型能够很好地模拟桩端的应力-沉降关系.
|
图 4 砂土中桩端应力-沉降关系与反演拟合 Figure 4 Comparison between fitted and measured relationship of pile-end stress and settlement in sand |
|
图 5 软土中桩端应力-沉降关系与反演拟合 Figure 5 Comparison between fitted and measured relationship of pile-end stress and settlement in clay |
| 表 1 桩尺寸及Sbu和k2反演结果 Table 1 Pile size and back-analysis value of Sbu and k2 |
楔形单桩在分层土中的荷载-沉降曲线可按以下步骤得到:
1) 如图 6所示,将楔形桩按土层分布情况划分为n个单元,保证每个桩单元所在土层的均一性.

|
图 6 楔形单桩单元划分示意 Figure 6 Element partition of tapered single pile in multilayered soils |
2) 假设桩端沉降Sbn,根据假设的沉降大小,利用式(10)计算τb,并利用式(13)计算Pbn:
| $ {P_{{\rm{b}}n}} = {\rm{ \mathsf{ π} }}{r^2}{\tau _{\rm{b}}}. $ | (13) |
3) 假设第i单元底面的沉降为Sbi,轴力为Pbi;并假设第i单元桩中点部分沉降为Sci,(Sci初值取Sbi).将Sci代入式(1)计算第i单元中点处桩-土界面上的剪应力τsi,则第i单元桩的侧阻力ΔPi为
| $ \Delta {P_i} = 2{\rm{ \mathsf{ π} }}\left( {R - {z_i}\tan \alpha } \right){L_i}{\tau _{{\rm{s}}i}}. $ | (14) |
式中:zi为第i单元中点深度,Li为第i单元桩长.
4) 由力的平衡条件,可得第i单元桩顶部轴力:
| $ {P_{{\rm{t}}i}} = {P_{{\rm{b}}i}} + \Delta {P_i} = {P_{{\rm{b}}i}} + 2{\rm{ \mathsf{ π} }}\left( {R - {z_i}\tan \alpha } \right){L_i}{\tau _{{\rm{s}}i}}. $ | (15) |
5) 假设第i单元桩轴力沿桩长呈线性分布,可利用桩的压缩计算第i单元中点的沉降Sci′:
| $ {{S'}_{{\rm{c}}i}} = {S_{{\rm{b}}i}} + \left( {\frac{{{P_{{\rm{t}}i}} + 3{P_{{\rm{b}}i}}}}{8}} \right)\left[ {\frac{{{L_i}}}{{{E_{\rm{p}}}{\rm{ \mathsf{ π} }}{{\left( {R - {z_i}\tan \alpha } \right)}^2}}}} \right]. $ | (16) |
比较Sci和Sci′,重复步骤3~5直到满足误差要求,否则取Sci=Sci′.
6) 假设在计算第i单元桩的压缩量时轴力呈线性分布,则第i单元桩的顶部沉降为
| $ {S_{{\rm{t}}i}} = {S_{{\rm{b}}i}} + \left( {\frac{{{P_{{\rm{t}}i}} + {P_{{\rm{b}}i}}}}{2}} \right)\left[ {\frac{{{L_i}}}{{{E_{\rm{p}}}{\rm{ \mathsf{ π} }}{{\left( {R - {z_i}\tan \alpha } \right)}^2}}}} \right]. $ | (17) |
7) 将第(i-1)单元桩的底部沉降取为第i单元桩的顶部沉降(i=2, 3, 4…n):
| $ {S_{{\rm{b}}\left( {i - 1} \right)}} = {S_{{\rm{t}}i}},i = 2,3,4 \cdots n. $ | (18) |
8) 重复2~7步骤直到所有单元沉降和轴力求出.
9) 改变桩端沉降,重复上述步骤,得到不同桩端沉降条件下的桩顶部荷载与顶部沉降,从而得出楔形桩的荷载-沉降曲线.
2 楔形群桩荷载-沉降解析在相同荷载作用下群桩沉降往往比单桩大,产生“群桩效应”.为了考虑楔形群桩的“群桩效应”影响,本文将楔形群桩受荷后产生的沉降分为两部分:由自身顶部荷载引起的沉降和受其他桩影响而产生的沉降.其中第一部分沉降采用单桩理论计算;第二部分沉降[7, 16]则拆分为各个单桩之间的相互作用并考虑“加筋”与“遮帘”效应,最后进行线性叠加.
2.1 基本假定在楔形群桩荷载-沉降分析过程中作如下假定:
1) 承台与土体不接触,不考虑承台承担荷载;
2) 所有楔形桩的尺寸相同;
3) 桩体周围的土体为均匀理想弹塑性体,桩受到周围桩体的作用可以线性叠加计算[8, 16];
4) 桩-土界面满足理想摩擦定律,非受荷桩桩-土界面无相对滑动.
2.2 单桩与单桩相互作用分析桩与桩之间的相互作用是十分复杂的桩-土协同受力问题.本文将相互作用过程简化为三步分析:
1) 先不考虑非受荷桩的刚度,在受荷桩的作用下,周围的土体会产生一个自由沉降场.
2) 由于非受荷桩的存在,土体的实际沉降会小于1中的沉降,否则桩和土不满足变形协调条件.故在第1步中土体沉降场的作用下,非受荷桩与土发生相互协调作用,最后达到应力和沉降的平衡.
3) 非受荷桩与土层相互作用,在桩-土界面上产生剪力,分布剪力会使桩体产生附加沉降,将这部分“加筋”与“遮帘”效应[17]引起的桩、土沉降加上第2步中的沉降即为单桩-单桩相互作用下的最终沉降.
如图 7,在桩的顶部荷载P作用下桩体将带动临近土层发生沉降.用W11(z)表示荷载作用下桩自身的沉降,其周围土层的自由沉降场Us(s, z)可表示为[8]:

|
图 7 楔形单桩之间相互影响 Figure 7 Interaction between tapered piles |
| $ {U_{\rm{s}}}\left( {s,z} \right) = \left\{ {\begin{array}{*{20}{c}} {\frac{{\ln \left( {{r_{\rm{m}}}} \right) - \ln \left( s \right)}}{{\ln \left( {2{r_{\rm{m}}}} \right) - \ln \left( d \right)}}{W_{11}}\left( {\frac{d}{2},z} \right),\frac{d}{2} \le s < {r_{\rm{m}}};}\\ {0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;s \ge {r_{\rm{m}}}.} \end{array}} \right. $ | (19) |
当周围土层中存在非受荷桩时,土体的抗剪切能力加强,假设非受荷桩的沉降为W21(z),则非受荷桩的桩-土相对沉降为W21(z)-Us(s, z).
对非受荷桩上一微小段桩体进行受力分析,当微小段足够小时可视其为等截面桩:
| $ \frac{{\partial P}}{{\partial z}}{\rm{d}}z + q = 0, $ | (20) |
式中q为桩侧阻力,可表示为[8]
| $ q = {K_{zi}}\left( {{W_{21}}\left( z \right) - {U_{\rm{s}}}\left( {s,z} \right)} \right). $ | (21) |
式中:
由桩体的弹性压缩可得:
| $ P\left( z \right) = - {E_{{\rm{p}}i}}{A_{{\rm{p}}i}}\frac{{\partial {W_{21}}\left( z \right)}}{{\partial z}}. $ | (22) |
式中:Epi为第i单元桩弹性模量,Api为第i单元桩的平均截面面积.
将式(21)和(22)代入式(20)可得桩-桩之间相互影响的控制微分方程:
| $ {E_{{\rm{p}}i}}{A_{{\rm{p}}i}}\frac{{{\partial ^2}{W_{21}}\left( z \right)}}{{\partial {z^2}}} - {K_{zi}}\left( {{W_{21}}\left( z \right) - {U_{\rm{s}}}\left( {s,z} \right)} \right) = 0. $ | (23) |
由于楔形桩截面积与截面所在位置有关,因此式(23)没有解析解,本文利用有限差分法进行求解.
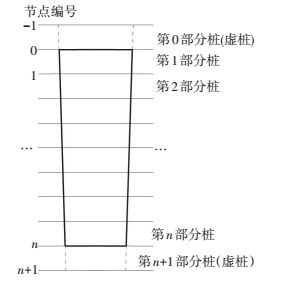
如图 8所示,将桩体分成n等份,在桩顶部和桩端部分别增加1个虚桩单元,得到n+2个离散桩单元和n+3个离散节点.利用式(19)求出n+1个实节点处的土体沉降Usi (i=0, 1…n),并采用中心差分格式来推导控制微分方程(23)的差分形式,各阶导数差分形式为
|
图 8 楔形单桩差分单元示意 Figure 8 Difference units of tapered single pile |
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}W}}{{{\rm{d}}z}}\left| {_{{z_i}}} \right. = \frac{{{W_{i + 1}} - {W_{i - 1}}}}{{2h}},\\ \frac{{\partial {W^2}}}{{{\partial ^2}z}}\left| {_{{z_i}}} \right. = \frac{{{W_{i + 1}} + {W_{i - 1}} - 2{W_i}}}{{{h^2}}}. \end{array} \right.其中\;h = \frac{L}{n},i = 0,1, \cdots n. $ | (24) |
将式(24)代入式(23)可得n+1个实桩单元控制微分方程的差分表达式为
| $ \begin{array}{*{20}{c}} {\frac{1}{{{h^2}}}\left( {{W_{i - 1}} + {W_{i + 1}}} \right) - \left( {\frac{2}{{{h^2}}} + \frac{{{K_{zi}}}}{{{E_{{\rm{p}}i}}{A_{{\rm{p}}i}}}}} \right){W_i} = - \frac{{{K_{zi}}U{s_i}}}{{{E_{{\rm{p}}i}}{A_{{\rm{P}}i}}}},}\\ {i = 0,1, \cdots n.} \end{array} $ | (25) |
非受荷桩边界条件为
| $ \left\{ \begin{array}{l} {P_0} = 0,\\ {P_n} = {k_1}{W_n}{A_n}. \end{array} \right. $ | (26) |
将式(24)代入式(26)可得边界条件的差分形式:
| $ \left\{ \begin{array}{l} {E_{{\rm{p}}0}}{A_{{\rm{p}}0}}\frac{1}{h}\left( {{W_1} - {W_{ - 1}}} \right) = 0,\\ {E_{{\rm{p}}n}}{A_{{\rm{p}}n}}\frac{2}{h}\left( {{W_{n + 1}} - {W_{n - 1}}} \right) - {k_1}{A_{{\rm{p}}n}}{W_n} = 0. \end{array} \right. $ | (27) |
将式(25)、(27)进行归并组合,写成矩阵形式:
| $ {\left[ {{\mathit{\boldsymbol{K}}_{ij}}} \right]_{\left( {n + 3} \right) \times \left( {n + 3} \right)}}\left\{ {{\mathit{\boldsymbol{W}}_{ij}}} \right\} = \left\{ {{\mathit{\boldsymbol{U}}_{ij}}} \right\}. $ | (28) |
式中:[Kij](n+3)×(n+3)为i桩与j桩之间的转移矩阵;{Wij}为j桩荷载引起i桩沉降向量;{Uij}为不考虑相邻桩i刚度时,由j桩顶部荷载引起i桩处土体沉降扩充向量.
实际上,群桩间约束作用增强了桩周土体的抗剪强度,产生“加筋”效应;同时,群桩间的相互作用被中间桩所遮挡而降低,产生“遮帘”效应.然而,实际计算过程中由于很难将“加筋”和“遮帘”效应分开考虑.因此,在群桩相互作用研究中通常[17]引入一个修正系数来考虑“加筋”和“遮帘”效应.如图 7所示,在受荷桩的影响下非受荷桩与土体发生相互作用,桩-土界面产生分布剪应力τ;这部分剪应力会在土体产生新的沉降场,使群桩产生新的沉降,产生“加筋”与“遮帘”效应.根据Randolph[1]提出的剪切位移理论,非受荷桩桩-土界面上剪应力τ引起周围桩的沉降为
| $ {{W'}_{12}} = \frac{{\tau d}}{{2{G_{\rm{s}}}}}\ln \left( {\frac{{{r_{\rm{m}}}}}{s}} \right). $ | (29) |
假设剪应力沿桩周长均匀分布:
| $ \tau = \frac{q}{{{\rm{ \mathsf{ π} }}d}} = \frac{{2{G_{\rm{s}}}}}{{d\ln \left( {2{r_{\rm{m}}}/d} \right)}}\left( {{W_{21}} - {U_{\rm{s}}}\left( {s,z} \right)} \right). $ | (30) |
联立式(29)、(30),可求得:
| $ \left| {{{W'}_{12}}} \right| = \left( {{U_{\rm{s}}}\left( {s,z} \right) - {W_{21}}} \right)\frac{{\ln \left( {{r_{\rm{m}}}} \right) - \ln \left( s \right)}}{{\ln \left( {2{r_{\rm{m}}}} \right) - \ln \left( d \right)}}. $ | (31) |
考虑相邻非受荷单桩“加筋”与“遮帘”效应的沉降折减系数为
| $ {\lambda _{{\rm{r12}}}} = \frac{{\left| {{{W'}_{12}}} \right|}}{{{W_{11}}}} = \left\{ \begin{array}{l} \frac{{{U_{\rm{s}}}\left( {s,z} \right) - {W_{21}}}}{{{W_{11}}}}\frac{{\ln \left( {{r_{\rm{m}}}} \right) - \ln \left( s \right)}}{{\ln \left( {2{r_{\rm{m}}}} \right) - \ln \left( d \right)}},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{d}{2} < s < {r_{\rm{m}}};\\ \;\;\;\;\;\;\;\;\;\;\;\;0,\;\;\;\;\;\;\;\;s \ge {r_{\rm{m}}}. \end{array} \right. $ | (32) |
同时考虑群桩间“加筋”与“遮帘”效应的沉降修正系数为
| $ {\beta _j} = \prod\limits_{i = 1}^m {\left( {1 - {\lambda _{{\rm{r}}ji}}} \right)} ,j = 1,2 \cdots m. $ | (33) |
式中m为群桩中的桩数.
求解式(28)可得到j桩顶部受荷而引起的i桩沉降向量{W}ij,取第2项Wij(0)即桩的顶部沉降.将所有顶部沉降分别乘以修正系数βj并相加,即可得出楔形群桩基础中任意桩的顶部沉降:
| $ {W_i}\left( 0 \right) = \sum\limits_{j = 0}^m {{W_{ij}}\left( 0 \right){\beta _j}} ,i = 1,2 \cdots m. $ | (34) |
群桩基础根据承台性状不同可分为柔性承台群桩和刚性承台群桩.两种群桩在荷载传递上不同在于:柔性群桩荷载均分,群桩沉降中间大两边小;刚性承台荷载分布中间小两边大,群桩沉降均匀.按照承载特性将楔形群桩的荷载-沉降曲线分为两种情况求解:
1) 当承台为绝对柔性时,将承台总荷载均分给各个桩,其求解步骤为:
(1) 假设所有桩的初始端部沉降Sbi(m)相同,取为Sbi(m)=Sb.然后按照单桩方法求出顶部荷载Pi.
(2) 然后将Pi作为已知条件,依次按式(19)~(34)进行求解,即可得出楔形群桩基础中任意桩的顶部沉降Wi(0).
(3) 改变桩端沉降,重复上述步骤,得到相应桩端沉降条件下的群桩顶部荷载与顶部沉降,从而得出楔形群桩的荷载-沉降曲线.
2) 当承台为绝对刚性时,荷载分布情况未知,需增加约束条件:
| $ {W_1}\left( 0 \right) = {W_2}\left( 0 \right) = \cdots = {W_{\rm{m}}}\left( 0 \right). $ | (35) |
利用试算方法迭代求解.具体过程为:
(1) 将荷载均分给各个桩,假设所有桩的初始端部沉降相同,取为Sbi(m)=Sb.
(2) 根据桩端沉降Sbi(m)按照单桩方法求出桩顶部荷载Pi.
(3) 然后将Pi作为已知条件,并依次按式(19)~(34)求解桩顶部沉降.
(4) 将原来桩的端部沉降Sbi(m)加上其顶部沉降Wi(0)与群桩平均顶部沉降之差的二分之一作为新的桩端沉降Sbi(m),重复第(2)、(3)步求出所有桩的顶部沉降.
(5) 重复第(4)步直到每根桩顶部沉降与群桩平均顶部沉降之差满足要求.
(6) 改变桩端沉降,重复上述步骤(1)~(5),得到相应桩端沉降条件下的群桩顶部荷载与顶部沉降,从而得出楔形群桩的荷载-沉降曲线.
3 验证与分析为了证明本文提出计算方法的有效性,将本文楔形单桩及楔形群桩计算结果与已有试验进行对比.
3.1 算例1文献[6]通过楔形单桩的室内模型试验探究了楔形单桩的承载特性与荷载-沉降关系.试验中测得的桩体、土体参数见表 2.其将桩-土的荷载-沉降关系假设为双曲线模型,求导后得到了桩体的抗剪刚度,再通过逐渐增加微小沉降得到了楔形桩的荷载-沉降曲线;但是文献[6]方法中抗剪刚度参数的确定需要进行大量现场试桩试验,实际使用中不易操作.
| 表 2 试验1楔形桩与土体参数 Table 2 Properties of the tapered pile and the soil (Test 1) |

|
图 9 楔形单桩荷载-沉降曲线计算结果与试验结果对比 Figure 9 Comparisons between the predicted and the measured load-settlement of the tapered pile |
楔形桩长度为35 cm,桩顶直径为4 cm,桩端直径为1 cm.参考工程地质手册上相同土层的经验取值,土的弹性模量取压缩模量的2.2倍为4.5 MPa;土体剪切模量采用弹性理论公式计算:
| $ {G_{\rm{s}}} = \frac{{{E_{\rm{s}}}}}{{2\left( {1 + \nu } \right)}}. $ | (36) |
土体剪切模量值为1.67 MPa,k1利用式(11)计算结果为100.2 MN/m3,k2利用式(12)反演计算的结果为69.26 MN/m3,Sbu为4 mm.本文计算所得楔形桩荷载-沉降曲线与现场实测及文献[6]结果的对比见图 9.本文提出的简便计算方法得到的楔形单桩荷载-沉降曲线与实测和文献[6]拟合结果十分接近,本文计算参数物理意义更为明确,获取较方便.
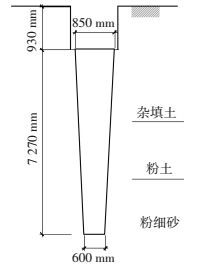
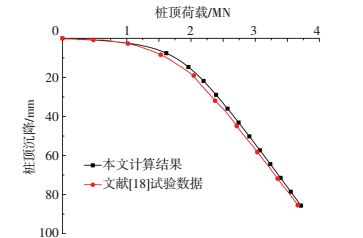
3.2 算例2文献[18]利用现场载荷试验对等截面桩、楔形桩及扩底桩的单桩竖向承载力及荷载-沉降曲线等问题进行了研究.如图 8所示,试桩场地土层主要有3层:杂填土、粉土、粉细砂.其中杂填土底面深度4.2~6.2 m, 粉土底面深度7.0~8.3 m,粉细砂顶面深度7.0~8.3 m;计算时取平均值.桩体尺寸见图 10,计算所需土体参数根据试桩结果反演求出,如表 3所示.土体剪切模量采用式(36)计算,k1利用式(11)计算取为80.28 MN/m3,k2通过反演计算取为78.77 MN/m3 (k1、k2相差很小,可能桩端土未达到硬化阶段),Sbu为20 mm.试验与计算得出的荷载-沉降曲线见图 11.本文计算结果与实测曲线吻合良好,说明本文计算方法适用于分层土中楔形单桩荷载-沉降曲线的预测.
| 表 3 试验2楔形桩与土体参数 Table 3 Properties of the tapered pile and the soil (Test 2) |
|
图 10 试验2现场土层分布及桩尺寸示意 Figure 10 Tapered pile and the profile of multilayered soils |
|
图 11 分层土中楔形单桩荷载-沉降曲线计算与试验结果对比 Figure 11 Comparison between the predicted and measured load-settlement of the tapered pile in multilayered soils |
文献[10]利用室内模型试验对楔形群桩和等截面群桩加固软弱地基的效果进行了研究.群桩荷载试验在3 m×3 m×3 m的室内基坑中进行,试验利用刚性承台对群桩进行加载.桩体采用C15混凝土浇筑.土的计算参数:土的压缩模量为8.5 MPa,泊松比为0.35,Gs按照文献[10]提供的方法计算:
| $ {G_{\rm{s}}} = {E_{\rm{s}}}\frac{{1 - 2{\nu ^2}}}{{2\left( {1 - {\nu ^2}} \right)}}. $ | (37) |
求出的土体剪切模量为3.66 MPa,楔形桩、等截面桩参数k1按照式(11)计算的结果分别为367.7 MN/m3及239.0 MN/m3,由于两种桩型荷载-沉降曲线较为平缓,故认为桩端土未达到硬化阶段.桩的计算参数见表 4.基于承台性状,利用绝对刚性承台楔形群桩计算方法求解荷载-沉降曲线;图 12给出了试验与计算的对比结果,可以看出本文计算结果与模型试验中的群桩荷载-沉降曲线很接近,故本文提出的刚性楔形群桩计算方法能够合理预测楔形群桩的荷载-沉降曲线.
| 表 4 试验3中桩体计算参数 Table 4 Parameters of the tapered pile |

|
图 12 楔形群桩荷载-沉降曲线计算结果与试验结果对比 Figure 12 Comparisons between the predicted and the measured load-settlement of tapered pile groups |
为了进一步探究楔形群桩和等截面群桩效应的特性,基于算例3的土层、桩体参数,用本文的计算方法得到了刚性承台下3×3群桩、2×2群桩、单桩等不同布桩方式的楔形桩、等截面桩的桩顶平均荷载-沉降曲线(见图 13).相同沉降条件下,3×3和2×2楔形群桩的桩顶平均荷载(P/m)十分接近,说明楔形群桩的群桩效应随桩数变化不明显.沉降较小时,2×2楔形群桩和楔形单桩刚度大于相同布置的等截面桩型,但沉降较大时,楔形桩刚度明显小于等截面桩;这可能是由于桩顶的沉降较大时,桩侧土强度完全发挥,桩刚度主要靠桩端提供,较小的桩端面积会导致楔形桩刚度小于等截面桩.

|
图 13 桩顶平均荷载与桩顶沉降的关系 Figure 13 Comparisons between the average load and settlement on the pile head |
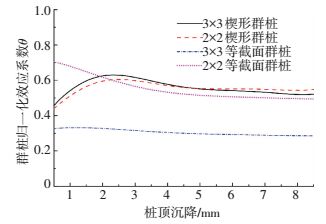
为了进一步对比两种桩型的群桩效应,本文将相同桩顶沉降条件下的群桩桩顶平均荷载与单桩桩顶荷载的比值定义为群桩归一化效应系数θ.图 14给出了群桩归一化效应系数θ与桩顶沉降的关系.等截面群桩的θ值随桩数的增大而减小,随着沉降的增大略有减小;楔形群桩的θ值随桩数变化并不明显,且随着沉降增大先增大后略有减小;楔形群桩的θ值比等截面群桩大,说明楔形群桩承载性能优于等截面群桩.
|
图 14 桩顶归一化效应系数与桩顶沉降的关系 Figure 14 Comparisons between the normalized coefficient for pile group and settlement on the pile head |
1) 将楔形桩桩侧和桩端的应力-沉降关系分别考虑成双曲线和双折线,可以对楔形单桩在土层中的荷载-沉降曲线进行有效预测.本文计算参数物理意义明确,获取方便.
2) 利用有限差分法求解楔形桩的桩-桩相互影响关系并考虑“加筋”与“遮帘”效应,得到了刚性和柔性承台下楔形群桩的荷载-沉降曲线计算方法,为楔形群桩变形分析计算提供了可行途径.
3) 算例分析表明,本文提出的楔形单桩、群桩荷载-沉降计算方法可以合理地预测其荷载-沉降曲线.
| [1] |
RANDOLPH M F, WROTH C P. Analysis of deformation of vertically loaded piles[J].
Journal of the Geotechnical Engineering Division. ASCE, 1978, 104(12): 1465-1488.
|
| [2] |
NORLUND R L. Bearing capacity of piles in cohensionless soils[J].
Journal of the Soil Mechanics, 1963, 89: 1-34.
|
| [3] |
ROBINSKY E I, MORRISON C F. Sand displacement and compaction around model friction piles[J].
Canadian Geotechnical Journal, 1964, 1(2): 81-93.
DOI: 10.1139/t64-002 |
| [4] |
陈龙珠, 梁国钱, 朱金颖. 桩的轴向荷载-沉降曲线的一种解析算法[J].
岩土工程学报, 1994, 16(6): 30-38.
CHEN Longzhu, LIANG Guoqian, ZHU Jinying. Analytical calculation of axial loading-settlement curve of piles[J]. Chinese Journal of Geotechnical Engineering, 1994, 16(6): 30-38. |
| [5] |
KRAFT L M, RAY R P, KAGAWA T. Theoretical t-z curves[J].
Journal of the Geotechnical Engineering Division, ASCE, 1981, 107(11): 1543-1561.
|
| [6] |
刘杰, 何杰, 闵长青. 楔形刚性桩与桩周土的非线性相互作用[J].
铁道学报, 2010, 32(2): 137-140.
LIU Jie, HE Jie, MIN Changqing. Nonlinear interaction between the rigid taper pile and pile-surrounding soil[J]. Journal of the China Railway Society, 2010, 32(2): 137-140. |
| [7] |
RANDOLPH M F, WROTH C P. An analysis of the vertical deformation of pile groups[J].
Géotechnique, 1979, 29(4): 423-439.
DOI: 10.1680/geot.1979.29.4.423 |
| [8] |
MYLONAKIS G, GAZETAS G. Settlement and additional internal forces of grouped piles in layered soil[J].
Géotechnique, 1998, 48(1): 55-72.
DOI: 10.1680/geot.1998.48.1.55 |
| [9] |
ZHANG Q Q, ZHANG Z M. A simplified calculation approach for settlement of single pile and pile groups[J].
Journal of Computing in Civil Engineering, 2012, 26(6): 750-758.
DOI: 10.1061/(ASCE)CP.1943-5487.0000167 |
| [10] |
刘杰, 何杰, 闵长青. 楔形桩与圆柱形桩复合地基承载性状对比研究[J].
岩土力学, 2010, 31(7): 2202-2206.
LIU Jie, HE Jie, MIN Changqing. Contrast research of bearing behavior for composite foundation with tapered piles and cylindrical piles[J]. Rock and Soil Mechanics, 2010, 31(7): 2202-2206. |
| [11] |
何杰, 刘杰, 张可能, 等. 夯实水泥土楔形桩复合地基承载特性试验研究[J].
岩石力学与工程学报, 2012, 31(7): 1506-1512.
HE Jie, LIU Jie, ZHANG Keneng, et al. Experimental study of bearing behavior of composite foundation with rammed soil-cement tapered piles[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(7): 1506-1512. |
| [12] |
LEE C Y. Pile group settlement analysis by hybrid layer approach[J].
Geotechnical Engineering Division, Proceedings of the American Society of Civil Engineers, 1993, 119(6): 984-997.
DOI: 10.1061/(ASCE)0733-9410(1993)119:6(984) |
| [13] |
刘建峰. 桩土界面摩擦特性试验研究[D]. 天津: 天津大学, 2008.
LIU Jianfeng. An experimental investigation on the interface friction between pile and soil[D]. Tianjin: Tianjin University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10056-2009072658.htm |
| [14] |
王浩, 周健, 邓志辉. 砂土中桩端阻力随位移发挥的内在机理研究[J].
岩土工程学报, 2006, 28(5): 587-593.
WANG Hao, ZHOU Jian, DENG Zhihui. Mobilization of toe resistance of piles with local displacement in sand[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(5): 587-593. |
| [15] |
张忠苗, 张乾青, 张广兴, 等. 软土地区大吨位超长试桩试验设计与分析[J].
岩土工程学报, 2011, 33(4): 535-543.
ZHANG Zhongmiao, ZHANG Qianqing, ZHANG Guangxing, et al. Large tonnage tests on super-long piles in soft soil area[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(4): 535-543. |
| [16] |
GUO W D, RANDOLPH M F. An efficient approach for settlement prediction of pile groups[J].
Géotechnique, 1999, 49(2): 161-179.
DOI: 10.1680/geot.1999.49.2.161 |
| [17] |
石名磊, 邓学钧, 刘松玉. 群桩间"加筋与遮帘"相互作用研究[J].
东南大学学报, 2003, 33(3): 343-346.
SHI Minglei, DENG Xuejun, LIU Songyu. Study of restrain effect among piles[J]. Journal of Southeast University, 2003, 33(3): 343-346. DOI: 10.3969/j.issn.1001-0505.2003.03.024 |
| [18] |
蒋建平, 高广运, 顾宝和. 扩底桩?楔形桩?等直径桩对比试验研究[J].
岩土工程学报, 2003, 25(6): 764-766.
JIANG Jianping, GAO Guangyun, GU Baohe. Comparison of belled pile, tapered pile and equal-diameter pile[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(6): 764-766. |
 2017, Vol. 49
2017, Vol. 49


