2. 同济大学 地下建筑与工程系,上海 200092
2. Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China
相对于等截面桩,楔形桩不仅可以节省材料而且能提高承载性能.然而,目前在工程中设计使用楔形桩时尚无设计标准可循,极大地限制了楔形桩的应用.
国内外许多学者对楔形桩的承载力性能进行了一系列有益研究:Norlund[1]、Robinsky等[2]分别利用现场试验和室内试验研究了楔形桩的承载性能,发现楔形摩擦桩比等截面摩擦桩承载力更大; Naggar等[3-4]和Wei等[5]利用模型试验研究了楔形桩的轴向承载性能和相应的沉降规律,结果表明当桩长径比小于20时楔形桩承载力的提高效果较为明显; 刘杰等[6]开展了楔形桩与等截面桩承载力的对比试验, 研究表明,在相同平均单位承载力条件下,楔形桩相比等截面桩节省材料约80%;蒋建平等[7-9]通过试验对比分析了楔形桩和等截面桩的承载力发现楔形桩比同体积的等截面桩承载力大(平均增大65.59 %)且沉降小(平均减小68.50 %); 王奎华等[10]基于极限平衡理论对楔形桩承载力进行了理论推导,然而其结果与实测结果有一定差距;王幼青等[11]基于半经验半理论的方法推导了楔形桩承载力计算公式;刘杰等[12]、何杰等[13]利用剪切位移法和室内试验对楔形桩承载力问题进行研究,结果表明楔形桩复合地基加固效果优于圆柱形桩复合地基;周航等[14]基于圆孔扩张理论对楔形桩挤土效应进行了理论研究,结果表明楔形桩的沉桩阻力随着楔形角、桩端直径及土体黏聚力的减小而减小;曹兆虎等[15]利用透明土材料对楔形桩的沉桩效应进行了研究,发现楔形桩静压过程中在地表附近桩周土体的影响范围大约为等混凝土用量等截面桩的1.2倍.
上述研究大多集中于楔形桩的荷载-沉降规律探究,相应的楔形桩承载力实验研究和理论研究也没有提出具体有效的力学计算方法,同时目前国内规范[16]没有针对楔形桩承载力计算的具体规定.本文利用经典弹塑性力学理论,提出了考虑桩-土相互作用机理的楔形桩极限承载力理论计算方法,并引入承载力增大系数研究了其承载力提高的机理.
1 楔形桩承载力解析 1.1 楔形桩受力破坏机理单桩在受竖向荷载作用直至破坏的过程中,桩周土体一般经过3个变形阶段:土体弹性变形阶段,土体部分弹性部分塑性变形阶段,土体塑性变形阶段;最后一个阶段桩基完全失效.基于楔形桩承载的发挥过程,可将楔形桩桩承载力发挥分为两个阶段:土体弹性变形阶段和挤土塑性破坏阶段.
土体弹性阶段桩与土之间的相互挤压作用不明显,桩与土之间无相对滑移,荷载变化不会引起桩-土界面上正应力的变化,仅会引起剪应力的变化,荷载主要由剪应力(即桩-土之间摩擦力)承担.在此阶段桩-土之间相互挤压作用较弱,因此理论上沉降较小,此阶段的最大荷载是楔形桩的临塑荷载.随着荷载的继续增大,桩-土之间的摩擦力不能完全承担外部荷载,于是桩-土之间发生相互挤压作用,引起桩-土之间正应力和剪应力[5]发生变化,桩-土之间进入挤土塑性破坏阶段.此时增加的荷载由桩-土界面上的正应力与剪应力共同承担,直至桩-土界面上土体发生剪切破坏,楔形桩承载力达到极限.在此阶段桩-土之间相互挤压作用较强,承载力发挥更为明显.
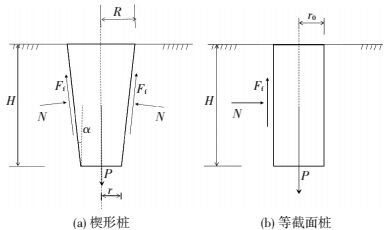
1.2 楔形桩力学模型楔形桩形状如图 1(a)所示:楔形角为α,桩长为H,桩顶半径为R,桩端半径为r.等截面桩如图 1(b)所示:桩长为H,桩半径为r0.假设外加荷载作用于桩轴线处,大小为P,桩-土界面上作用有正应力N和摩擦力Ff.
|
图 1 楔形桩和等截面桩力学模型 Figure 1 Mechanical model for tapered pile and uniform cross section pile |
假设楔形桩和等截面桩体积相同,且桩为理想刚性体(即桩体弹性模量远大于土体),同时假定土体在整个桩的作用范围内均匀,土压力沿深度线性分布,静止土压力系数K0;土体破坏时服从Mohr-Coulomb强度准则,土体黏聚力为c,内摩擦角为φ;桩-土之间摩擦系数为f.
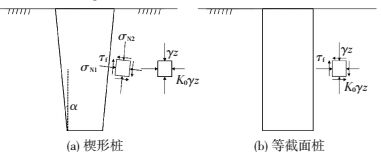
1.3 楔形桩受力破坏过程计算推导1) 第一受力阶段.桩与土之间无相对滑移,外加荷载主要由桩-土界面上摩擦力承担.如图 2(a)所示,荷载增加不会引起单元体应力σN1和σN2改变,仅会引起摩擦力(剪应力)τf变化.当无附加荷载时,z深处桩-土界面上土单元应力状态分析:
|
图 2 楔形桩和等截面桩桩土接触面土体单元分析 Figure 2 Soil element on pile-soil interface |
| $ {\sigma _z} = \gamma z, $ | (1) |
| $ {\sigma _r} = {K_0}\gamma z. $ | (2) |
式中:γ为土体重度,K0为静止土压力系数.
将土单元应力进行旋转得出平行于桩-土界面方向的土体单元应力状态:
| $ {\sigma _{{\rm{N1}}}} = {\sigma _z}{\sin ^2}\alpha + {\sigma _r}{\cos ^2}\alpha = \gamma z\left( {{{\sin }^2}\alpha + {K_0}{{\cos }^2}\alpha } \right), $ | (3) |
| $ {\sigma _{{\rm{N2}}}} = {\sigma _r}{\sin ^2}\alpha + {\sigma _z}{\cos ^2}\alpha = \gamma z\left( {{K_0}{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right). $ | (4) |

|
图 3 深度z处单位长度桩受力分析 Figure 3 Mechanical model for unit tapered pile at z depth |
将各项应力在轴向方向上投影,可进一步求得单位长度桩dh提供的承载力为
| $ {\rm{d}}{P_{1 - 1}} = 2{\rm{ \mathsf{ π} }}\left( {R - \frac{{R - r}}{H}z} \right){\sigma _{{\rm{N1}}}}\left( {\tan \alpha + f} \right){\rm{d}}h. $ | (5) |
P1-1为第一阶段楔形桩的承载力,由式(5)易知
| $ \frac{{\partial {P_{1 - 1}}}}{{\partial z}} = 2{\rm{ \mathsf{ π} }}\gamma z\left( {R - \frac{{R - r}}{H}z} \right)\left( {\tan \alpha + f} \right)\left( {{{\sin }^2}\alpha + {K_0}{{\cos }^2}\alpha } \right). $ | (6) |
已知桩长为H,对式(6)两边积分可得
| $ {P_{1 - 1}} = \frac{{\rm{ \mathsf{ π} }}}{3}\gamma \left( {R + 2r} \right){H^2}\left( {\tan \alpha + f} \right)\left( {{{\sin }^2}\alpha + {K_0}{{\cos }^2}\alpha } \right). $ | (7) |
楔形桩体积为
| $ {V_{楔}} = \frac{{\rm{ \mathsf{ π} }}}{3}\left( {{R^2} + Rr + {r^2}} \right)H. $ | (8) |
等截面桩可视为特殊的楔形桩,其楔形角α为0,等截面桩桩长为H,半径为r0.代入楔形桩的计算公式中,等截面桩承载力P0为
| $ {P_0} = {\rm{ \mathsf{ π} }}\gamma {K_0}f{r_0}{H^2}. $ | (9) |
等截面桩体积为
| $ {V_0} = {\rm{ \mathsf{ π} }}r_0^2H. $ | (10) |
假设两种桩型体积相同,有如下关系:
| $ r = \frac{1}{6}\left( {\sqrt {36r_0^2 - 3{H^2}{{\tan }^2}\alpha } - 3H\tan \alpha } \right). $ | (11) |
为反映楔形桩承载力相对等截面桩的提高效果,本文将相同土层及界面参数、相同受力阶段下等体积楔形桩承载力与等截面桩承载力的比值定义为楔形桩承载力增大系数.因此将两种桩型承载力式(7)、(9)进行对比可以得到第一受力阶段的承载力增大系数为
| $ \begin{array}{l} {\omega _1} = \frac{{\sqrt {36r_0^2 - 3{H^2}{{\tan }^2}\alpha } - H\tan \alpha }}{{6f{K_0}{r_0}}}\left( {\tan \alpha + f} \right) \times \\ \;\;\;\;\;\;\;\left( {{{\sin }^2}\alpha + {K_0}{{\cos }^2}\alpha } \right). \end{array} $ | (12) |
在分层土地基中,楔形摩擦桩的承载力计算公式可由分层计算结果的叠加来表示:
| $ \begin{array}{l} {P_{1 - 1}} = \frac{{\rm{ \mathsf{ π} }}}{3}\sum\limits_{i = 1}^n {\left\{ {{\gamma _i}\left[ {3R\left( {Z_{i + 1}^2 - Z_i^2} \right) + 2\tan \alpha \left( {Z_{i + 1}^3 - Z_i^3} \right)} \right] \times } \right.} \\ \;\;\;\;\;\;\;\;\;\left. {\left( {\tan \alpha + {f_i}} \right)\left( {{{\sin }^2}\alpha + {K_{0i}}{{\cos }^2}\alpha } \right)} \right\}. \end{array} $ | (13) |
式中:Ri和ri为第i层土中桩体最大与最小桩径;Zi为第i层土上表面离地表深度;γi为第i层土平均重度;fi为第i层土中桩-土界面摩擦系数;K0i为第i层土静止土压力系数.
同理,分层土中等截面桩承载力计算公式为
| $ {P_0} = {\rm{ \mathsf{ π} }}{r_0}\sum\limits_{i = 1}^n {{\gamma _i}{K_{0i}}{f_i}\left( {Z_{i + 1}^2 - Z_i^2} \right)} . $ | (14) |
分层土中楔形桩第一阶段承载力增大系数为
| $ \begin{array}{l} {\omega _1} = \frac{{{P_{1 - 1}}}}{{{P_0}}} = \sum\limits_{i = 1}^n {\left\{ {\frac{{{\gamma _i}\left[ {3R\left( {Z_{i + 1}^2 - Z_i^2} \right) + 2\tan \alpha \left( {Z_{i + 1}^3 - Z_i^3} \right)} \right]}}{{3{r_0}\sum\limits_{j = 1}^n {{\gamma _j}{K_{0j}}{f_j}\left( {Z_{j + 1}^2 - Z_j^2} \right)} }} \times } \right.} \\ \;\;\;\;\;\;\;\left. {\left( {\tan \alpha + {f_i}} \right)\left( {{{\sin }^2}\alpha + {K_{0i}}{{\cos }^2}\alpha } \right)} \right\}. \end{array} $ | (15) |
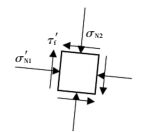
2) 第二受力阶段.摩擦力不足以承担增加的荷载,外加荷载会同时引起桩-土界面上正应力和剪应力变化.假设正应力与剪应力增大的同时摩擦系数不变,桩与土相互挤压过程中,周围土体仅仅沿桩-土界面上产生正应力和剪应力变化;垂直于桩-土界面方向的正应力变化很小,可以忽略不计(即挤土过程中图 2(a)σN2大小不会变化).如图 4所示对破坏时深度z处桩-土界面上土体进行单元应力分析,桩-土界面上正应力和剪应力分别为σN1′、τf′.桩-土界面上土体剪应力等于桩-土界面上摩擦力,故有
|
图 4 破坏条件时桩-土界面处土体单元应力分析 Figure 4 Stress analysis of soil element on pile-soil interface at failure condition |
| $ {{\tau '}_{\rm{f}}} = {{\sigma '}_{{\rm{N1}}}}f. $ | (16) |
土体发生破坏时满足Mohr-Coulomb准则,故桩-土界面上土体的主应力σ1、σ3满足以下条件
| $ \left( {\frac{{{\sigma _1} + {\sigma _3}}}{2} + c\cot \varphi } \right)\sin \varphi = \frac{{{\sigma _1} - {\sigma _3}}}{2}. $ | (17) |
对于一般应力状态下,桩-土界面上土体应力大小与其主应力有如下关系:
| $ \frac{{{\sigma _1} + {\sigma _3}}}{2} = \frac{{{{\sigma '}_{{\rm{N1}}}} + {\sigma _{{\rm{N2}}}}}}{2}, $ | (18) |
| $ \frac{{{\sigma _1} - {\sigma _3}}}{2} = \sqrt {{{\left( {\frac{{{{\sigma '}_{{\rm{N1}}}} + {\sigma _{{\rm{N2}}}}}}{2}} \right)}^2} + \tau _{\rm{f}}^{'2}} . $ | (19) |
将式(16)~(19)联立可求得
| $ {{\sigma '}_{{\rm{N1}}}} = \frac{{{\sigma _{{\rm{N2}}}}\left( {1 + {{\sin }^2}\varphi } \right) + 2c\cot \varphi {{\sin }^2}\varphi }}{{4{f^2} + {{\cos }^2}\varphi }} + \frac{{2\sqrt {\sigma _{{\rm{N2}}}^2\left( {{{\sin }^2}\varphi - {f^2}{{\cos }^2}\varphi } \right) + {c^2}{{\cos }^2}\varphi \left( {1 + 4{f^2}} \right) + {\sigma _{{\rm{N2}}}}c{{\sin }^2}\varphi \left( {1 + 2{f^2}} \right)} }}{{4{f^2} + {{\cos }^2}\varphi }}. $ | (20) |
对于正常固结黏土和砂土,黏聚力c一般较小.为计算方便,假设黏聚力c取0,可将式(20)写为
| $ {{\sigma '}_{{\rm{N1}}}} = \frac{{1 + {{\sin }^2}\varphi + 2\sqrt {{{\sin }^2}\varphi - {f^2}{{\cos }^2}\varphi } }}{{4{f^2} + {{\cos }^2}\varphi }}{\sigma _{{\rm{N2}}}}. $ | (21) |
若黏聚力不可忽略,可求出等效内摩擦角φ′代替φ代入式(21)求解.等效内摩擦角φ′满足:
| $ \begin{array}{*{20}{c}} {\frac{{1 + {{\sin }^2}\varphi ' + 2\sqrt {{{\sin }^2}\varphi ' - {f^2}{{\cos }^2}\varphi '} }}{{4{f^2} + {{\cos }^2}\varphi '}}{\sigma _{{\rm{N2}}}} = \frac{{{\sigma _{{\rm{N2}}}}\left( {1 + {{\sin }^2}\varphi } \right) + 2c\cot \varphi {{\sin }^2}\varphi }}{{4{f^2} + {{\cos }^2}\varphi }} + }\\ {\frac{{2\sqrt {\sigma _{{\rm{N2}}}^2\left( {{{\sin }^2}\varphi - {f^2}{{\cos }^2}\varphi } \right) + {c^2}{{\cos }^2}\varphi \left( {1 + 4{f^2}} \right) + {\sigma _{{\rm{N2}}}}c{{\sin }^2}\varphi \left( {1 + 2{f^2}} \right)} }}{{4{f^2} + {{\cos }^2}\varphi }}.} \end{array} $ | (22) |
将式(4)代入可将式(21)化简为
| $ \begin{array}{l} {{\sigma '}_{{\rm{N1}}}} = \frac{{1 + {{\sin }^2}\varphi + 2\sqrt {{{\sin }^2}\varphi - {f^2}{{\cos }^2}\varphi } }}{{4{f^2} + {{\cos }^2}\varphi }}\gamma z \times \\ \;\;\;\;\;\;\;\;\;\left( {{K_0}{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right). \end{array} $ | (23) |
同理,第二受力阶段极限承载力P1-2为
| $ \begin{array}{l} \frac{{\partial {P_{1 - 2}}}}{{\partial z}} = 2{\rm{ \mathsf{ π} }}\gamma z\left( {R - \frac{{R - r}}{H}z} \right)\left( {\tan \alpha + f} \right)\left( {{K_0}{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right) \times \\ \;\;\;\;\;\;\;\;\;\;\;\frac{{1 + {{\sin }^2}\varphi + 2\sqrt {{{\sin }^2}\varphi - {f^2}{{\cos }^2}\varphi } }}{{4{f^2} + {{\cos }^2}\varphi }}. \end{array} $ | (24) |
对式(24)两边积分可得
| $ \begin{array}{l} {P_{1 - 2}} = \frac{{\rm{ \mathsf{ π} }}}{3}\gamma \left( {R + 2r} \right){H^2}\left( {\tan \alpha + f} \right)\left( {{K_0}{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right) \times \\ \;\;\;\;\;\;\;\;\;\frac{{1 + {{\sin }^2}\varphi + 2\sqrt {{{\sin }^2}\varphi - {f^2}{{\cos }^2}\varphi } }}{{4{f^2} + {{\cos }^2}\varphi }}. \end{array} $ | (25) |
同理可求得第二受力阶段的承载力增大系数为
| $ \begin{array}{l} {\omega _2} = \frac{{{P_{1 - 2}}}}{{{P_0}}} = \frac{{\left( {\sqrt {36r_0^2 - 3{H^2}{{\tan }^2}\alpha } - H\tan \alpha } \right)\left( {\tan \alpha + f} \right)}}{{6f{K_0}{r_0}\left( {4{f^2} + {{\cos }^2}\varphi } \right)}} \times \\ \;\;\;\;\;\;\;\left( {{K_0}{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right)\left( {1 + {{\sin }^2}\varphi + 2\sqrt {{{\sin }^2}\varphi - {f^2}{{\cos }^2}\varphi } } \right). \end{array} $ | (26) |
同理分层土中第二阶段承载力增大系数为
| $ \begin{array}{l} {\omega _2} = \frac{{{P_{1 - 2}}}}{{{P_0}}} = \\ \sum\limits_{i = 1}^n {\left\{ {\frac{{{\gamma _i}\left[ {3R\left( {Z_{i + 1}^2 - Z_i^2} \right) + 2\tan \alpha \left( {Z_{i + 1}^3 - Z_i^3} \right)} \right]\left( {\tan \alpha + {f_i}} \right)}}{{3{r_0}\left( {4f_i^2 - {{\cos }^2}{\varphi _i}} \right)\sum\limits_{j = 1}^n {{\gamma _j}{K_{0j}}{f_j}\left( {Z_{j + 1}^2 - Z_j^2} \right)} }} \times } \right.} \\ \left. {\left( {{{\sin }^2}\alpha + {K_{0i}}{{\cos }^2}\alpha } \right)\left( {1 + {{\sin }^2}{\varphi _i} + 2\sqrt {{{\sin }^2}{\varphi _i} - {f^2}{{\cos }^2}{\varphi _i}} } \right)} \right\}. \end{array} $ | (27) |
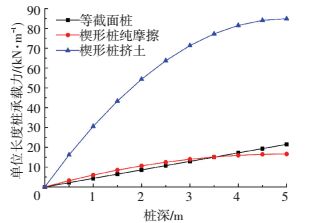
假设土体静止土压力系数为0.3,土体的内摩擦角为25°,桩-土界面的摩擦系数为0.3;楔形桩楔形角为2°,楔形桩桩底半径为0.4 m,桩长为5 m,图 5给出了楔形桩、等截面桩沿桩长方向的单位承载力.
|
图 5 沿桩长方向单位长度桩提供承载力变化 Figure 5 Variation of unit pile bearing capacity along pile |
在土压力线性变化的假定下:等截面桩的单位承载力呈线性变化;而楔形桩则呈非线性变化,刚开始时增长较快,到某一深度后基本不变化.楔形桩上部分桩体在承载力中占较大部分.实际上桩的承载力也同样从上到下逐渐发挥的;楔形桩体上半部分承担荷载比例大,故在相同沉降条件下楔形桩的承载力更大.
2.2 承载力增大系数影响因素分析由上述分析可知,楔形桩承载力增大系数主要与桩-土界面上摩擦力系数f、静止土压力系数K0、楔形角α、土体摩擦角φ密切相关.为研究上述参数对楔形桩承载力增大系数的影响,计算分析时改变相应参数,其余参数按2.1节取值.
1) 桩-土界面上摩擦力系数f的影响
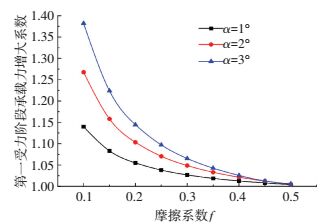
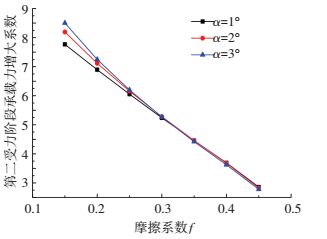
图 6、7为3个不同楔形角的楔形桩承载力增大系数ω1、ω2与桩-土界面上摩擦系数f的关系.ω1随着f增大有逐渐减小的趋势,最后趋于一个定值;但相比而言ω2随着f增大而减小得更快.这是由于楔形桩承载力由桩-土界面摩擦力和正应力共同提供,当f增大时,摩擦力所占部分增大,正应力提供的承载力基本不变,总的算来ω1、ω2减小;在挤土阶段,f越大土体破坏时桩-土界面正应力越小;弹性变形阶段,桩-土界面上正应力不变,因此f对ω2影响更明显.
|
图 6 桩-土界面摩擦系数对ω1的影响 Figure 6 Effect of friction coefficient at pile-soil interface on bearing capacity augmentation factor ω1 |
|
图 7 桩-土界面摩擦系数对ω2的影响 Figure 7 Effect of friction coefficient at pile-soil interface on bearing capacity augmentation factor ω2 |
2) 静止土压力系数K0的影响
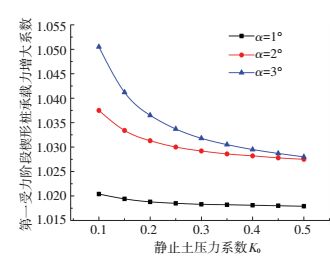
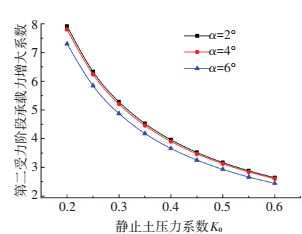
图 8、9是3种不同楔形角的楔形桩的承载力增大系数随K0变化的关系.随着K0增大,ω1、ω2逐渐减小并最终趋于一个定值.K0越大越不利于楔形桩承载力的发挥.
|
图 8 静止土压力系数对ω1的影响 Figure 8 Effect of coefficient of earth pressure at rest on bearing capacity augmentation factor ω1 |
|
图 9 静止土压力系数对ω2的影响 Figure 9 Effect of coefficient of earth pressure at rest on bearing capacity augmentation factor ω2 |
3) 楔形角α的影响
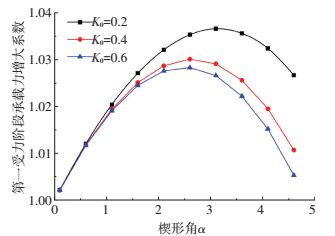
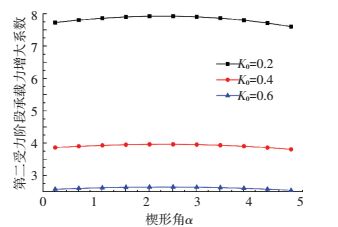
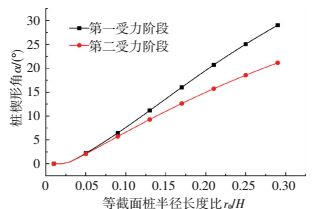
图 10、11表示在3种不同土体静止土压力系数K0情况下楔形角α对第一、二受力阶段承载力增大系数的影响.ω1、ω2随α角增大先增大后减小.从图 10、11可看出:一定条件下,第一、第二受力阶段的桩都有一个最佳的楔形角;即在同体积条件下,具有该楔形角的楔形桩承载力增大系数最大.通过计算,图 12给出桩的最佳楔形角随等截面桩的半径长度比变化的关系.在半径长度比较小时,最佳楔形角变化较缓慢(楔形桩承载力提高效果不明显);稍大后,最佳楔形角几乎随半径长度比呈线性增长.第二受力阶段的最佳楔形角略小于第一阶段.
|
图 10 楔形角对ω1的影响 Figure 10 Effect of taper angle on bearing capacity augmentation factor ω1 |
|
图 11 楔形角对ω2的影响 Figure 11 Effect of taper angle on bearing capacity augmentation factor ω2 |
|
图 12 最佳楔形角随桩半径长度比的变化 Figure 12 Effect of pile radius-length ratio on best taper angle |
4) 土体内摩擦角φ的影响
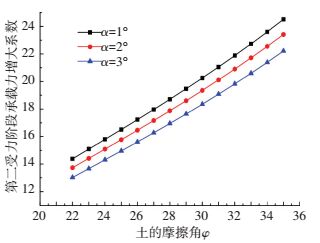
图 13研究了土体内摩擦角对第二受力阶段承载力增大系数ω2的影响.ω2随φ呈近似直线增长.不同楔形角之间的关系曲线近似平行.
|
图 13 土的内摩擦角φ对ω2的影响 Figure 13 Effect of friction angle φ on bearing capacity augmentation factor ω2 |
为了验证本文理论推导结果的可靠性,将理论推导结果和国外几位学者的研究试验结果进行对比.
试验1是Naggar等[3]研究楔形桩的轴向承载性能的模型试验.试验采用相对密度为18.4%的松散砂土;采用实验室制作的钢桩模型,保证了桩体相对土体的相对刚性状态.试验时,土体未达到完全塑性破坏,因此本文将弹性阶段承载力与试验结果对比.计算P1-1时采用与文献中试验结果平均值接近的桩-土界面摩擦系数(f取为0.8),静止土压力系数采用Jaky[17-18]公式计算:
| $ {K_0} = 1 - \sin \varphi . $ | (28) |
土体重度为16.3 kN/m3,内摩擦角为32°.将理论计算结果与试验对比, 见图 14.桩长较小时,楔形桩和等截面桩的承载力无论是模型试验还是理论计算都很接近,可见长径比较小时,楔形桩的承载力提高不能有效发挥;桩长为5 m时,0.6°楔形角的楔形桩模型试验和理论计算结果得出的ω1分别为1.07和1.20,0.95°楔形桩相应的结果分别为1.26和1.26, 结果接近.由于试验结果表明桩的摩擦系数随围压变化,而本文理论计算时取定值,导致了理论计算结果和试验的误差.
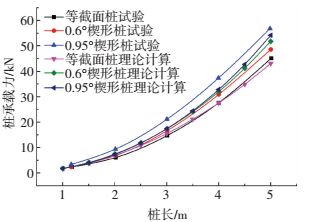
|
图 14 试验1与理论计算对比 Figure 14 Comparison of pile shaft resistance reported by Naggar[3](Test 1) and predicted by theory calculation |
试验2为Naggar[4]等研究楔形桩轴向极限承载性能的离心机试验.离心机试验使用均匀的砂土和钢管模型桩,并在10 g加速度下得出了相应的等截面桩与楔形桩的荷载-沉降曲线.根据实验结果,利用太沙基及Poulos等提出的两种不同方法来得出桩体的极限承载力.试验材料参数见表 1,桩-土界面摩擦因数取为0.42,内摩擦角为30°,静止土压力系数采用式(28)计算.表 2是理论计算极限承载力与试验结果对比.用Poulos方法时,1号桩试验与理论得出的ω2分别为1.90和1.72,误差率为9%;2号桩ω2分别为1.68与1.71,误差率为1.8%.
| 表 1 试验1桩参数 Table 1 Geometry parameter of piles for Test 1 |
| 表 2 理论计算极限承载力和试验2结果对比 Table 2 Comparison of tapered pile ultimate bearing capacity reported by Naggar [4] (Test 2) and predicted by theory calculation |
从以上两个试验与理论计算对比可以看出,采用本文的理论计算方法得出的承载力计算结果基本与文献中的试验结果吻合.
4 结论1) 基于荷载作用下楔形桩-土之间相互作用的基本机理,利用Mohr-Coulomb强度准则提出了楔形桩在两个受力阶段的承载力计算公式.通过与模型试验结果的对比发现,本文提出的理论方法能够较为合理地计算出楔形桩的承载力,并且该方法力学意义明确,计算相对快捷.但没有考虑土体的非线性,故此方法有待进一步的改进与完善.
2) 在土压力线性变化的假定下:等截面桩的单位长度承载力呈线性变化;楔形桩的则呈非线性变化,刚开始时增长较快,到某一深度后基本不变化.
3) 桩-土界面摩擦因数、静止土压力系数、楔形角与土体内摩擦角对楔形桩的承载力增大系数均有影响.其中,楔形桩的承载力增大系数随着土体内摩擦角的增加而增加,但随静止土压力系数和桩-土界面摩擦系数的增加而减小, 同时存在特定的楔形角使得承载力增大系数最大.
| [1] |
NORLUND R L. Bearing capacity of piles in cohesionless soils[J].
Journal of the Soil Mechanics, 1963, 89: 1-34.
|
| [2] |
ROBINSKY E I, MORRISON C F. Sand displacement and compaction around model friction piles[J].
Canadian Geotechnical Journal, 1964, 1(2): 81-93.
DOI: 10.1139/t64-002 |
| [3] |
NAGGAR M H E, WEI J Q. Axial capacity of tapered piles established from model tests[J].
Canadian Geotechnical Journal, 1999, 36(6): 1185-1194.
DOI: 10.1139/t99-076 |
| [4] |
NAGGAR M H E, SAKR M. Evaluation of axial performance of tapered piles from centrifuge tests[J].
Canadian Geotechnical Journal, 2000, 37(6): 1295-1308.
DOI: 10.1139/t00-049 |
| [5] |
WEI Jinqi, NAGGAR M H E. Experimental study of axial behaviour of tapered piles[J].
Canadian Geotechnical Journal, 1998, 35(4): 641-654.
DOI: 10.1139/t98-033 |
| [6] |
刘杰, 王忠海. 楔形桩承载力试验研究[J].
天津大学学报(自然科学与工程技术版), 2002, 35(2): 257-260.
LIU Jie, WANG Zhonghai. Experimental study on the bearing capacity of wedge pile[J]. Journal of Tianjin University (Science and Technology), 2002, 35(2): 257-260. |
| [7] |
蒋建平. 楔形桩的研究与应用综述[J].
施工技术, 2006, 35(1): 37-40.
JIANG Jianping. Introduction of study and application of tapered piles[J]. Construction Technology, 2006, 35(1): 37-40. |
| [8] |
蒋建平, 高广运, 顾宝和. 扩底桩?楔形桩?等直径桩对比试验研究[J].
岩土工程学报, 2003, 25(6): 764-766.
JIANG Jianping, GAO Guangyun, Gu Baohe. Comparison of belled pile, tapered pile and equal-diameter pile[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(6): 764-766. |
| [9] |
蒋建平, 高广运. 桩单位体积承载力问题探讨[J].
工业建筑, 2006, 36(9): 43-45, 67.
JIANG Jianping, GAO Guangyun. Study on bearing capacity per volume of bored-cast-place piles[J]. Industrial Construction, 2006, 36(9): 43-45, 67. |
| [10] |
王奎华, 吴文兵, 叶良, 等. 基于极限平衡理论的楔形桩承载力计算方法[J].
建筑科学与工程学报, 2009, 26(4): 108-113.
WANG Kuihua, WU Wenbing, YE Liang, et al. Calculation method of bearing capacity of tapered pile based on limit equilibrium theory[J]. Journal of Architecture and Civil Engineering, 2009, 26(4): 108-113. |
| [11] |
王幼青, 王仙蔚. 楔形桩的承载能力研究[J].
低温建筑技术, 2008, 30(6): 112-113.
WANG Youqing, WANG Xianwei. Study on the bearing capacity of the wedge pile[J]. Low Temperature Architectural Technology, 2008, 30(6): 112-113. |
| [12] |
刘杰, 何杰, 闵长青, 等. 楔形桩与圆柱形桩复合地基承载性状对比研究[J].
岩土力学, 2010, 31(7): 2202-2206.
LIU Jie, HE Jie, MIN Changqing, et al. Contrast research of bearing behavior for composite foundation with tapered piles and cylindrical piles[J]. Rock and Soil Mechanics, 2010, 31(7): 2202-2206. |
| [13] |
何杰, 刘杰, 闵长青, 等. 楔形刚性桩承载特性室内模型试验研究[J].
公路工程, 2008, 33(1): 7-9.
HE Jie, LU Jie, MIN Changqing, et al. Experimental study on characteristic of behavior of tapered rigid pile[J]. Highway Engineering, 2008, 33(1): 7-9. |
| [14] |
周航, 孔纲强, 刘汉龙. 基于圆孔扩张理论的静压楔形桩沉桩挤土效应研究[J].
中国公路学报, 2014, 27(4): 24-30.
ZHOU Hang, KONG Gangqiang, LIU Hanlong. Study on pile sinking compaction effect of hydrostatic wedge pile using cavity expansion theory[J]. China Journal of Highway and Transport, 2014, 27(4): 24-30. |
| [15] |
曹兆虎, 孔纲强, 周航, 等. 基于透明土的静压楔形桩沉桩效应模型试验研究[J].
岩土力学, 2015, 36(5): 1363-1367.
CAO Zhaohu, KONG Gangqiang, ZHOU Hang, et al. Model test on installation effect of tapered piles in transparent soils[J]. Rock and Soil Mechanics, 2015, 36(5): 1363-1367. |
| [16] |
中华人民共和国住房和城乡建设部. 建筑桩基技术规范: JGJ 94—2008 [S]. 北京: 中国建筑工业出版社, 2008.
Ministry of Housing and Urban-Rural Construction of the People's Republic of China.Technical code for building pile foundation:JGJ 94—2008 [S]. Beijing: China Architecture and Building Press, 2008. |
| [17] |
JAKY J. Pressure in soils[C]//Processing of the 2nd International Conference on soil Mechanic and Foundation Engineering Rotterdam. Rotterdam, Balkema:[s.n.], 1948: 103-107.
|
| [18] |
JAKY J. The coefficient of earth pressure at rest[J].
Journal for Society of Hungarian Architects and Engineers, 1944: 355-358.
|
| [19] |
赵春风, 于明章, 吴水根, 等. 试桩未达破坏时单桩极限承载力的估算方法[J].
同济大学学报(自然科学版), 1999, 27(4): 474-477.
ZHAO Chunfeng, YU Mingzhang, WU Shuigen, et al. Method defining the bearing of single testing pile not reaching degree of failure[J]. Journal of Tongji University (Natural Science), 1999, 27(4): 474-477. |
 2017, Vol. 49
2017, Vol. 49


