2. 浙江省交通规划设计研究院,杭州 310006
2. Zhejiang Provincial Institute of Communications Planning, Design & Research, Hangzhou 310006, China
涡激振动是大跨度桥梁在低风速易发的具有强迫和自激双重性质的自限幅风致振动现象.日本东京湾通道桥(Trans-Tokyo Bay Bridge)、巴西里约尼泰罗伊大桥(Rio-Niteroi Bridge)、丹麦的大带桥(Great East Belt Bridge)和中国的西堠门大桥都曾发生过竖弯涡振[1-5].尽管涡激振动不会像颤振或驰振那样导致发散,但可影响行车安全,甚至诱发拉索参数共振等其他类型的气动不稳定问题.目前,涡振研究方法主要有理论分析、现场实测、数值模拟和风洞试验[6].表 1列举了大跨桥梁涡振代表性研究成果.
| 表 1 大跨桥梁涡振代表性研究成果 Table 1 Representative progress of VIV in long-span bridges |
上述研究针对不同主梁断面外形桥梁的涡振问题,提供了研究涡振机理的不同思路和方法,显示了涡振研究方法的多样性.在涡振研究过程中,研究手段不断演进,由最初的刚体模型测振、测压过渡到同步测力测振、同步测压测振风洞试验,研究方法从单独的试验研究、数值模拟、现场实测或理论分析发展到试验与数值模拟相结合、试验与理论分析相结合以及试验与实测相结合,分析方法则从二维涡振分析发展到三维涡振分析方法.
由于风洞试验测压法具有可直接得到箱梁表面气动力及其压力分布的优点,很多学者基于大跨度桥梁涡振性能优化,对比研究不同气动措施或气动外形下箱梁表面风压特性,从而揭示涡振机理[13-14, 21].然而,截止目前系列研究一定程度上忽视了涡振过程中箱梁表面气动力演变特性.Li等[4-5]基于西堠门大桥涡振现场实测,发现在涡振起始阶段,旋涡脱落发生在开槽及尾流区域;在锁定区,由于振动幅值增大,涡脱加强,并扩展到整个下游下表面.Kuroda[22]通过数值方法,发现不同攻角下扁平箱梁断面表面压力分布及绕流特点体现在气动力上,最终决定了结构是否发生涡振及涡振振幅的大小.总之,涡振过程中随着结构表面旋涡演化,引起气动力特性的变化,最终导致涡振响应的演变.综上,从涡振过程表面气动力演变特性的角度来揭示涡振机理十分重要.
针对大跨度桥梁典型流线型扁平箱梁主梁断面,开发了同步测力、测振和测压风洞试验装置,并在此基础上,研究了涡振过程(发生前、锁定区上升区、振幅极值点、下降区和涡振后)箱梁表面分布气动力演变特性,揭示了典型流线型箱梁断面涡振机理.主要研究内容包括平均压力系数、脉动压力系数和气动力频谱演化规律.
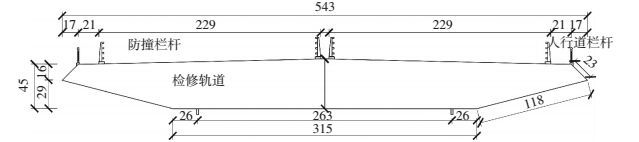
1 风洞试验 1.1 模型设计与同步测量试验装置研究对象为流线型闭口箱梁断面,采用几何缩尺比为1:70,模型长度L为1 700 mm,特征宽度B为543 mm,特征高度D为45 mm,长宽比(模型长度与主梁断面宽度之比)为3.13:1,表面布置有防撞栏、人行道栏杆和检修轨道等附属设施,主梁断面尺寸见图 1.
|
图 1 主梁节段模型断面尺寸(几何缩尺比1:70,单位mm) Figure 1 Geometrical sizes of a bridge sectional model with geometric scale of 1:70 (mm) |
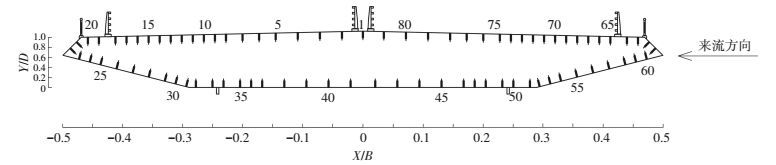
试验模型由两根长1 700 mm,壁厚1 mm,截面尺寸为50 mm×50 mm的薄壁空心铝方管纵梁和6个薄壁空心铝横梁构成的框架提供模型整体刚度;纵梁和横梁固定焊接,并在横梁上开孔,以便在不削弱总体刚度条件下便于测压管路的通过,见图 2(a)和(b).人行道栏杆和防撞栏均采用ABS板激光雕刻而成,如图 2(c)和(d)所示.模型外衣采用轻质航空木板制成,并在模型中部断面布置分布式测压孔,共81个测点,测压点之间的距离为10~20 mm,测压管内径为0.8 mm,长度均为1 200 mm,如图 3所示.图中,X/B和Y/D为无量纲坐标,X、Y分别指代主梁上下表面、迎背风侧测点坐标.

|
图 2 模型细部构造 Figure 2 Local views of the bridge-deck sectional model |
|
图 3 断面测压点编号与布置 Figure 3 Layout and IDs of pressure measured taps |
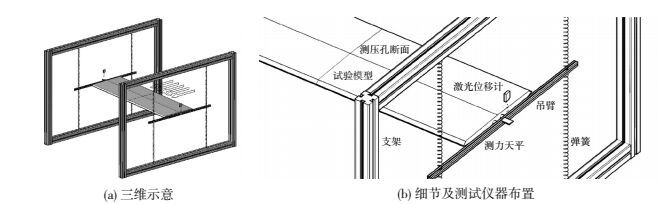
节段模型安装于自行研制装配式可调整风洞内支架系统上,保证模型两端与支架系统内壁间隙足够小且在试验中不会发生接触,最大限度避免模型端部三维绕流效应.模型采用双侧共4个天平与2根刚性水平吊臂相连;吊臂两端再分别通过上下共8根弹簧与框架系统相连,形成二维弹性悬挂系统,同时在吊臂处共布置两个激光位移传感器,见图 4、5.
|
图 4 同步测力、测压和测振节段模型试验示意 Figure 4 Schematic diagram of synchronal measurement systems |

|
图 5 同步测力、测压和测振节段模型安装 Figure 5 Testing model and synchronal measurement systems in TJ-3 wind tunnel |
试验采用日本Matsushita公司MLS LM10-130 ANR1215型激光位移传感器,测量范围为130±50 mm,分辨率为20 μm,线性度误差在±0.2%以内.模型表面压力测试使用美国SCANIVALVE扫描阀公司生产的量程为±254和±508 mm水柱的DSM3000电子式压力扫描阀系统、PC机和自编的信号采集软件.采样频率200 Hz,采样时间60 s.测力天平采用自主研制的高精度测力天平,见图 6.

|
图 6 高精度动态天平及其复合连接件 Figure 6 High precision dynamic balance and accessories |
试验在同济大学TJ-3边界层风洞中进行.该风洞是一个竖向布置的闭口回流式边界层风洞,试验段长14 m、宽15 m、高2 m,空风洞可控风速范围为1~17.6 m/s.试验过程最大阻塞比小于5%.测压管路的加长会使管路系统的固有频率降低,使压力信号中的高频成分发生显著衰减,影响测量精度.采用测压管路频响函数对测压信号进行修正.图 7为试验测得测压管路频响函数的幅值和相位.可知,在低频处,本试验采用测压管路系统对系统频响特性影响较小.利用集成式NI采集板对不同接口采集力信号和位移信号,并对测压点信号采用测压管路修正频响函数进行修正,从而由测控硬件条件和数值补偿修正实现了力信号、压力信号、与振动信号的一致同步性.主梁节段模型的主要参数见表 2.结合图 7可知,在竖弯和扭转频率处,压力信号畸变对幅值和相位影响较小,竖向频率处幅值比和相位差分别仅为1.01和-4.2°.

|
图 7 测压管路修正频响函数 Figure 7 Frequency response transfer function of the pressure measurement system |
| 表 2 主梁节段模型主要参数 Table 2 Main parameters of the model |
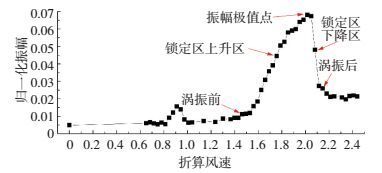
试验完成-3°、0°和+3°初始风攻角下的涡振试验,试验风速为2~7.5 m/s,对应基于主梁特征宽度的雷诺数范围为7.34×104~2.75×105.-3°和0°初始风攻角下,并未发现明显的涡振现象.+3°攻角下,主梁断面出现了明显的竖向涡振现象,涡振响应如图 8所示.横坐标表示折算风速U*=U/fhB,其中U为来流风速,fh为零风速下竖弯频率;纵坐标表示归一化振幅A/D,其中A为竖向振幅.在折算风速小于2.43的风速范围内,存在两阶竖弯涡振区.其中第二阶涡振锁定区间为1.53~2.11,最大振幅为0.067,对应折算风速为2.02.
|
图 8 节段模型竖弯涡振响应 Figure 8 Vertical VIV responses during VIV |
限于篇幅,仅针对第二阶涡振锁定区进行分析.为了研究涡振过程箱梁表面分布气动力演变特性,取折算风速1.46、1.76、2.02、2.08和2.15分别作为涡振发生前、锁定区上升区、振幅极值点、下降区和涡振后等不同时期的典型风速,并分别对上述风速下箱梁表面气动力进行分析研究.以下如无特别说明,均以上述风速点代替上述涡振不同时期.
2 分布气动力演变特性箱梁表面压力包含了丰富的信息,不仅能够反映断面气体绕流情况,而且通过积分还能获得气动力变化的整体过程及变迁过程.分布气动力为测点附近区域所受气动力,采用测点压力与相邻两测点距离一半的乘积来表示.对模型表面所有分布气动力进行代数叠加,即可得模型所受总气动力.根据节段模型表面压力信号,对比分析涡振前、锁定区上升区、振幅极值点、下降区以及涡振后等涡振不同时期箱梁表面分布气动力分布特征及演变特性,分析内容包括时域内的压力系数均值、压力系数根方差及各测点气动力频谱.
测点风压系数定义为
| ${C_{pi}}\left( t \right) = \frac{{{p_i}\left( t \right)}}{{1/2\rho U_0^2}}.$ | (1) |
式中:pi(t)为i测点风压时程,U0为相应工况下来流平均风速,Cpi(t)为i测点风压系数时程.
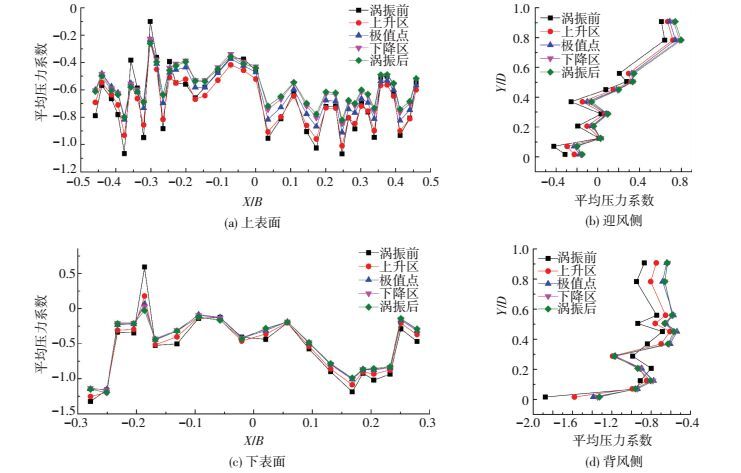
2.1 平均压力系数平均风压系数表征气流在模型表面总体分布特征,从而初步判断气流在箱梁表面的分离与再附.图 9给出了涡振过程平均风压系数空间分布演变特征.仅迎风侧风嘴上部及下部前端为正压区,其余均为负压区;上表面下游X/B=-0.30处和下表面下游X/B=-0.19处分别存在较大极值,表明气流在迎风侧前端分离后,在这些区域表面再附.涡振过程中,平均压力系数在箱梁表面空间分布保持稳定.
|
图 9 涡振过程平均风压系数 Figure 9 Comparison of mean pressure coefficients during VIV |
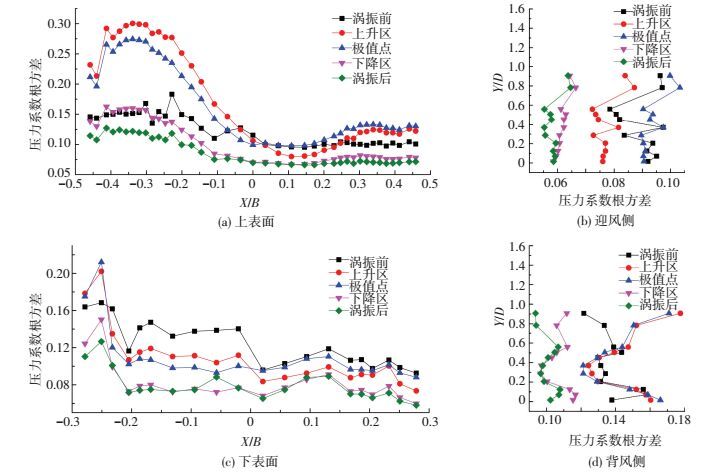
箱梁振动中,压力均值提供静力部分,而动荷载部分由压力脉动部分提供,表面压力根方差反映断面上压力脉动强弱.图 10给出了涡振过程箱梁表面压力系数根方差空间分布演变特征.涡振发生前,模型运动幅值很小,接近于静止,此时箱梁表面压力脉动分布均匀且压力系数根方差较小;进入涡振锁定区后,上表面下游、下表面下游与下游风嘴转角区域附近的压力根方差系数迅速增大,远大于涡振前;从极值点到涡振后,压力脉动迅速减弱;涡振后,箱梁表面的压力脉动基本处于分布均匀状态,接近涡振前的情况.整个涡振过程中,上表面下游(X/B<-0.1区域)、下表面下游与风嘴转角区域(-0.27<X/B<-0.23区域及背风侧Y/D<0.07区域)压力系数根方差演变特性最为明显,分别定义为区域A和区域B,见图 11.
|
图 10 涡振过程压力系数根方差 Figure 10 Comparison of RMS of pressure coefficients during VIV |

|
图 11 典型测点布置 Figure 11 Schematic of typical pressure taps |
为了进一步揭示涡振过程涡振幅值与气动力特性之间的同步演变关系,选取上表面X/B=-0.41、下表面X/B=-0.25处测点分别作为上表面下游、下表面下游与下游风嘴转角区域典型测点进行分析,并分别以A和B测点表达,见图 11.
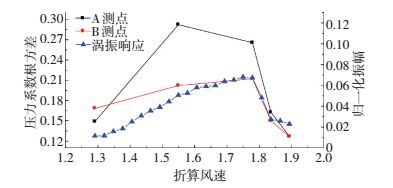
图 12给出了涡振过程A和B测点压力系数根方差与归一化振幅关系.涡振振幅与B测点压力系数根方差呈正相关关系,均在振幅极值点风速时达到最大,A测点压力系数根方差也与振幅有同步变化关系,A和B测点压力脉动与涡振振幅具有明显的相关性.
|
图 12 涡振过程压力系数根方差与涡振振幅同步演化关系 Figure 12 Comparison of RMS of pressure coefficients and amplitudes of VIV responses during VIV |
涡振过程中,箱梁表面压力系数根方差具有明显的变迁过程.涡振前和涡振后,模型表面的压力脉动分布相似,分布状态较均匀.而进入涡振锁定区后,由于模型振动造成的气流周期性分离与再附,导致上表面下游、下表面下游与下游风嘴转角区域的压力脉动明显,该压力脉动表现出明显的演化特性,这些区域的强烈压力脉动与涡振效应高度相关.
2.3 测点气动力频谱测点压力频谱能反映压力脉动的频率特征.经过对模型表面各测点压力进行频谱分析,发现涡振锁定区前后结构表面压力没有比较统一的卓越频率.而在涡振锁定区,结构周围旋涡脱落被结构振动锁定,表面压力存在着与结构振动一致的卓越频率.
定义无量纲气动力系数:
| $C_{pi}^d = \frac{{p_i^d}}{{1/2\rho U_0^2}},$ | (2) |
式中:pid为i测点压力在振动卓越频率处压力幅值,Cpid为i测点振动卓越频率处压力系数.
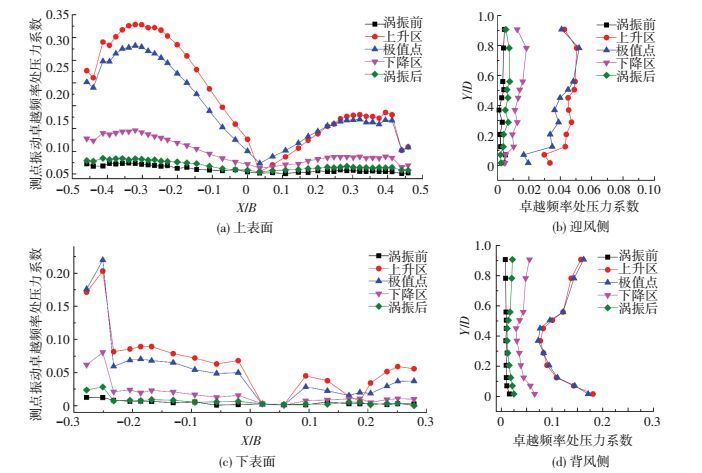
图 13给出了涡振过程各测点振动卓越频率处压力系数Cpid空间分布演变特征.涡振发生前后,各测点振动卓越频率处压力系数Cpid在运动卓越频率处的幅值很小且分布均匀,进入涡振锁定区后,箱梁绝大部分区域气动力系数幅值迅速增大,振幅极值点风速后,迅速衰减,并趋近于均匀分布.这表明涡振充分发展后,箱梁表面各点压力脉动主要是模型振动诱导产生的自激成分,而强迫力成分相对较小.
|
图 13 涡振过程测点振动卓越频率处压力系数 Figure 13 Comparison of pressure coefficients at predominant frequency during VIV |
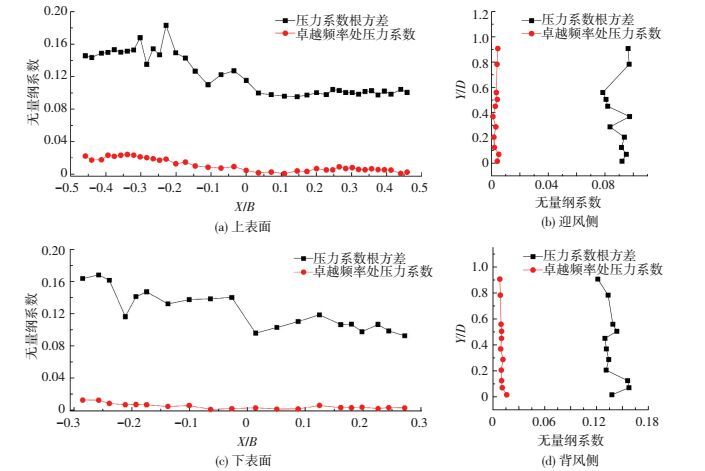
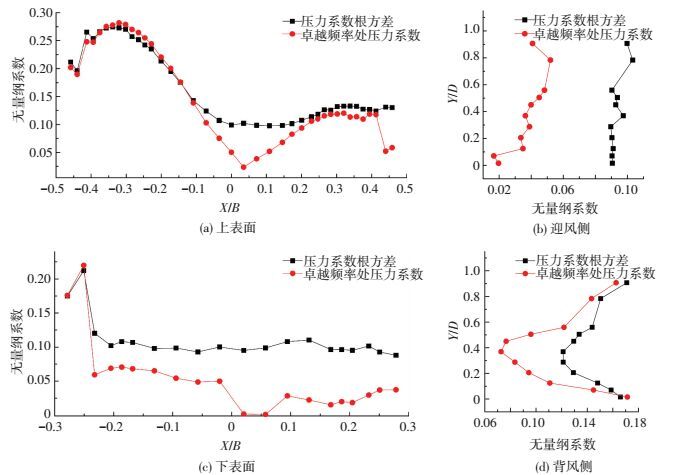
与图 10对比,可见测点振动卓越频率处压力系数空间分布与压力系数根方差空间分布相近.为了进一步展现上述两种分布之间的内在联系,以涡振前(折算风速为1.46)和振幅极值点(折算风速为2.02)为例,图 14、15分别给出了涡振前和振幅极值点时各测点振动卓越频率处压力系数Cpid与压力系数根方差空间分布对比.可见涡振前卓越频率处压力系数Cpid幅值与压力系数根方差相差迥异,在振幅极值点时,在上表面下游和下表面与下游风嘴转角区域,二者趋势完全相吻,即这些测点区域压力脉动几乎完全由模型振动诱导产生的自激成分贡献.
|
图 14 测点压力系数根方差与卓越频率处压力系数对比(涡振前) Figure 14 Comparison of RMS of pressure coefficients and pressure coefficients at predominant frequency (U*=1.46) |
|
图 15 测点压力系数根方差与卓越频率处无量纲气动力系数对比(振幅极值点) Figure 15 Comparison of RMS of pressure coefficients and pressure coefficients at predominant frequency (U*=2.02) |
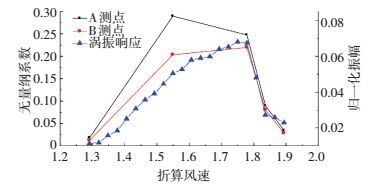
为了表征涡振过程涡振振幅与卓越频率处分布气动力之间的同步演变关系,与上节类似,以A和B测点分别作为上表面下游、下表面下游与下游风嘴转角区域典型测点.图 16给出了涡振过程A、B测点振动卓越频率处压力系数Cpid与归一化振幅关系.涡振振幅与B测点卓越频率处压力系数呈正相关关系,均在振幅极值点风速时达到最大,A测点卓越频率处压力系数也与振幅有同步变化关系.由模型周期性振动引起的A和B测点压力与涡振振幅高度相关.
|
图 16 涡振过程卓越频率处压力系数与振幅同步演化关系 Figure 16 Comparison of pressure coefficients at predominant frequency and amplitudes of VIV responses during VIV |
在涡振锁定区内,结构周围旋涡脱落被结构振动锁定,箱梁表面气动力变化主要由卓越频率主导.其中,上表面下游、下表面下游与下游风嘴转角区域气动力脉动几乎完全由该卓越频率主导的气动力分量贡献,即这些区域的压力脉动主要由旋涡脱落诱发的箱梁周期性运动引起的.综合2.1节和2.2节,可推断这些区域的强烈压力脉动是引起涡激共振的主要原因.
3 结论针对典型扁平箱梁主梁断面,开发了同步测力测振测压风洞试验装置,研究了涡振过程(发生前、锁定区上升区、锁定区振幅极值点、锁定区下降区和涡振后)箱梁表面分布气动力演变特性,揭示了典型流线型箱梁断面涡振机理.主要结论如下:
1) 涡振过程中,箱梁表面分布气动力特性具有明显的变迁过程,集中体现在涡振锁定区内外气动力特性具有显著差异.涡振发生前后,压力系数根方差较小、分布均匀且无统一卓越频率;涡振锁定区内,表面压力被结构振动锁定,压力脉动频率与结构频率一致.特别是上表面下游、下表面下游与下游风嘴转角区域的压力脉动明显,并几乎完全由模型周期性振动诱导产生的自激力成分贡献.
2) 涡振过程中,分布气动力与涡振振幅具有明显同步演化关系,压力系数根方差、振动卓越频率处压力系数等与涡振振幅高度相关.
3) 涡振过程分布气动力特性与涡振响应同步演化,尤其是上表面下游、下表面与下游风嘴转角附近区域气动力演变特性显著,是引起涡振的主要原因.
| [1] |
LARSEN A, ESDAHL S, ANDERSEN J E, et al. Storebælt suspension bridge-vortex shedding excitation and mitigation by guide vanes[J].
Journal of Wind Engineering & Industrial Aerodynamics, 2000, 88(2/3): 283-296.
|
| [2] |
FUJINO Y. Wind-Induced vibration and control of Trans-Tokyo Bay Crossing Bridge[J].
Journal of Structural Engineering, 2002, 128(8): 1012-1025.
DOI: 10.1061/(ASCE)0733-9445(2002)128:8(1012) |
| [3] |
BALLISTA R C, PFEIL M S. Reduction of vortex-induced oscillations of Rio-Nileroi bridge by dynamic control devices[J].
Journal of Wind Engineering and Industrial Aerodynamics, 2000, 84(3): 273-288.
DOI: 10.1016/S0167-6105(99)00108-7 |
| [4] |
LI H, LAIMA S, OU J, et al. Investigation of vortex-induced vibration of a suspension bridge with two separated steel box girders based on field measurements[J].
Engineering Structures, 2011, 33(6): 1894-1907.
DOI: 10.1016/j.engstruct.2011.02.017 |
| [5] |
LI H, LAIMA S, ZHANG Q, et al. Field monitoring and validation of vortex-induced vibrations of a long-span suspension bridge[J].
Journal of Wind Engineering & Industrial Aerodynamics, 2014, 124(7): 54-67.
|
| [6] |
许福友, 丁威, 姜峰, 等. 大跨度桥梁涡激振动研究进展与展望[J].
振动与冲击, 2010, 29(10): 40-49.
XU Fuyou, DING Wei, JIANG Feng, et al. Research progress and prospect of vortex-induced vibration of long-span bridges[J]. Journal of Vibration and Shock, 2010, 29(10): 40-49. DOI: 10.3969/j.issn.1000-3835.2010.10.009 |
| [7] |
SIMIU E, SCANLAN R H.
Wind effects on structures: Fundamentals and applications to design[M]. 2nd ed. New York: John Wiley & Sons, Inc, 1986.
|
| [8] |
LARSEN A. A generalized model for assessment of vortex-induced vibrations of flexible structures[J].
Journal of Wind Engineering and Industrial Aerodynamics, 1995, 57(2/3): 281-294.
|
| [9] |
LARSEN A, WALTHER J H. Aeroelastic analysis of bridge girder sections based on discrete vortex simulations[J].
Journal of Wind Engineering & Industrial Aerodynamics, 1997, 67(97): 253-265.
|
| [10] |
NAGAO F, UTSUNOMIYA H, YOSHIOKA E, et al. Effects of handrails on separated shear flow and vortex-induced oscillation[J].
Journal of Wind Engineering & Industrial Aerodynamics, 1997, 69(97): 819-827.
|
| [11] |
DIANA G, RESTA F, BELLOLI M, et al. On the vortex shedding forcing on suspension bridge deck[J].
Journal of Wind Engineering & Industrial Aerodynamics, 2006, 94(5): 341-363.
|
| [12] |
张文明, 葛耀君, 杨詠昕, 等. 带挑臂箱梁涡振气动控制试验[J].
哈尔滨工业大学学报, 2010, 42(12): 1948-1952, 1989.
ZHANG Wenming, GE Yaojun, YANG Yongxin, et al. Experimental study on aerodynamic control of the vortex-induced vibrations of a box girder with projecting slab[J]. Journal of Harbin Institute of Technology, 2010, 42(12): 1948-1952, 1989. DOI: 10.11918/j.issn.0367-6234.2010.12.021 |
| [13] |
许福友, 林志兴, 李永宁, 等. 气动措施抑制桥梁涡振机理研究[J].
振动与冲击, 2010, 29(1): 73-76.
XU Fuyou, LIN Zhixing, LI Yongning, et al. Study on the mechanism of vibrating vibration of bridge by aerodynamic measures[J]. Journal of Vibration and Shock, 2010, 29(1): 73-76. |
| [14] |
郭增伟, 赵林, 葛耀君, 等. 基于桥梁断面压力分布统计特性的抑流板抑制涡振机理研究[J].
振动与冲击, 2012, 31(7): 89-94.
GUO Zengwei, ZHAO Lin, GE Yaojun, et al. Mechanism analysis for vortex-induced vibration reduction of a flat streamlined steel box-shaped girder with airflow-suppressing board based on statistical property of surface pressure[J]. Journal of Vibration and Shock, 2012, 31(7): 89-94. |
| [15] |
胡传新, 杨立坤, 周志勇. 动态测压与POD方法相结合对桥梁涡振的分析[J].
力学季刊, 2013, 34(4): 591-598.
HU Chuanxin, YANG Likun, ZHOU Zhiyong. Research on vortex vibration of bridge based on POD and dynamic pressure measurement[J]. Chinese Quarterly of Mechanics, 2013, 34(4): 591-598. |
| [16] |
WU T, KAREEM A. Vortex-induced vibration of bridge decks: A volterra series based model[J].
Journal of Engineering Mechanics ASCE, 2013, 139(12): 1831-1843.
DOI: 10.1061/(ASCE)EM.1943-7889.0000628 |
| [17] |
MASHNAD M, JONES N P. A model for vortex-induced vibration analysis of long-span bridges[J].
Journal of Wind Engineering & Industrial Aerodynamics, 2014, 134: 96-108.
|
| [18] |
LAIMA S, LI H. Effects of gap width on flow motions around twin-box girders and vortex-induced vibrations[J].
Journal of Wind Engineering & Industrial Aerodynamics, 2015, 139: 37-49.
|
| [19] |
YUAN W Y, LAIMA S, CHEN W L, et al. Investigation on the vortex-and-wake-induced vibration of a separated-box bridge girder[J].
Journal of Fluids and Structures, 2017, 70: 145-161.
DOI: 10.1016/j.jfluidstructs.2017.01.015 |
| [20] |
XU K, ZHAO L, GE Y J. Reduced-order modeling and calculation of vortex-induced vibration for large-span bridges[J].
Journal of Wind Engineering & Industrial Aerodynamics, 2017, 167: 228-241.
|
| [21] |
XU F Y, YING XY, LI Y L, et al. Experimental explorations of the torsional vortex-induced vibrations of a bridge deck[J].
Journal of Bridge Engineering, 2016, 21(12): 1-10.
|
| [22] |
KURODA S. Numerical simulation of flow around a box girder of a long span suspension bridge[J].
Journal of Wind Engineering & Industrial Aerodynamics, 1997, 67(4): 239-252.
|
 2017, Vol. 49
2017, Vol. 49


