2. 哈尔滨工业大学 土木工程学院,哈尔滨 150090;
3. 深圳奥意建筑工程设计有限公司,广东 深圳 518000
2. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China;
3. Shenzhen A+E Design Co., Ltd., Shenzhen 518000, Guangdong, China
钝体绕流时,将产生复杂的流动分离及一系列的旋涡脱落及破碎,从而在钝体表面及附近产生显著的脉动压力场,进而诱发较大的气动噪声.这个问题在高速列车、航空航天和土木工程中广泛存在.
随着运行速度的不断提高,高速列车所产生的气动噪声迅速增大.与此同时,由于轮轨噪声已得到有效控制,从而使气动噪声可能超越轮轨噪声成为主要的噪声源.过大的气动噪声不仅严重影响乘客的乘坐舒适度和铁路沿线人员的正常生活,还可能引起列车系统结构以及铁路沿线相关设备的疲劳破坏,这些问题严重制约了列车运行速度的进一步提高[1].Talotte等[2]研究表明,受电弓气动噪声是高速列车所产生的气动噪声中的重要组成部分,因此研究杆件的低噪声技术是降低受电弓气动噪声乃至高速列车气动噪声的关键技术基础.
大型客机在起飞和着陆的过程中会在低空飞行很长距离,使得大片区域暴露在飞机产生的噪声环境中;与此同时,外部噪声通过飞机侧壁传到机舱内部,严重影响乘客的飞行体验[3].飞机噪声主要包括发动机噪声和机体气动噪声,但随着新技术的发展和应用,发动机噪声已经大为降低,使得机体气动噪声占据飞机噪声的主体地位[4].Chow等[5]对空中客车A340进行实测发现,起落架所产生的气动噪声是飞机进场及离场的主要噪声源.
无论是高速列车的受电弓,还是飞机的起落架,其装置主要都是由钝体杆件构成的.本文从气动噪声产生的源头角度研究钝体绕流的气动噪声源特性,结合Realizable k-ε湍流模型和宽频带噪声源模型方法模拟不同截面形式及尺寸的钝体在不同来流风速下气动噪声源的分布情况,探讨钝体表面气动噪声源强度及其分布的影响参数和影响机制.通过对简单钝体模型气动噪声源特性的研究,为加强各领域对气动噪声的认识奠定基础,同时也可为工程设计中降低气动噪声强度提供参考.
1 数值模拟方法钝体绕流气动噪声源的数值模拟方法主要分两个步骤:第一步,采用基于Realizable k-ε湍流模型的RANS方法计算钝体绕流的稳态流场参数;第二步,采用宽频带噪声源模型(broadband noise sources model)计算钝体表面的两个气动噪声源参数,即声功率级和表面声功率级.文献[6-9]的研究结果表明,采用Realizable k-ε湍流模型与宽频带噪声源模型相结合的方法来研究钝体的气动噪声源特性是合理的,所得结果也将是正确的.
1.1 Realizable k-ε湍流模型本文采用Realizable k-ε湍流模型来计算钝体绕流的稳态流场,并获得平均速度、湍动能和湍流耗散率等参数.该湍流模型由Shih等[10]于1995年提出,其控制方程为:
| $\frac{\partial }{{\partial t}}\left( {\rho k} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho k{u_i}} \right) = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _i}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} - \rho \varepsilon ,$ | (1) |
| $\begin{array}{l} \frac{\partial }{{\partial t}}\left( {\rho \varepsilon } \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho \varepsilon {u_i}} \right) = \\ \quad \quad \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _i}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \rho {C_1}S\varepsilon - \rho {C_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {v\varepsilon } }}. \end{array}$ | (2) |
式中:
Realizable k-ε湍流模型可准确地模拟大曲率流动、分离流、旋转流、以及带方向压强梯度的边界层流等问题.
1.2 宽频带噪声源模型宽频带噪声源模型不需要任何控制方程的瞬态求解,所有的源模型参数都可由定常RANS方法计算得到,有助于快速确定噪声源的主要区域.在ANSYS Fluent中提供了两种声源模型,即偶极子声源模型和四极子声源模型.偶极子声源模型关注偶极子声源,它主要由物体表面的脉动压力引起;四极子声源模型关注四极子声源,也就是湍流噪声,它主要由分离流和边界层流的湍流脉动引起.
1) 偶极子声源模型.Curle[11]方程主要解决气体流经静止物体表面所产生的噪声问题,基于Curle方程可以近似获得物体表面声源对总声功率的贡献.首先,远场声接收点的声压可以表示为
| $p'\left( {\vec x,t} \right) = \frac{1}{{4{\rm{ \mathsf{ π} }}{c_0}}}\int_S {\frac{{\left( {{x_i} - {y_i}} \right){n_i}}}{{{r^2}}}} \frac{{\partial p}}{{\partial t}}\left( {\vec y,\tau } \right){\rm{d}}S\left( {\vec y} \right).$ | (3) |
式中:p′为声压;c0为声速;
利用式(3),声源点辐射的声强可近似表示为
| $\begin{array}{l} I \approx \overline {{p^{'2}}} /{\rho _0}{c_0} = \frac{1}{{16{\rho _0}{{\rm{ \mathsf{ π} }}^2}c_0^3}}\int_S {\frac{{{\rm{co}}{{\rm{s}}^2}\theta }}{{{r^2}}}} \overline {{{\left[ {\frac{{\partial p}}{{\partial t}}\left( {\vec y,\tau } \right)} \right]}^2}} \times \\ \quad \quad {A_{\rm{c}}}\left( {\vec y} \right){\rm{d}}S\left( {\vec y} \right). \end{array}$ | (4) |
式中:ρ0为空气密度, θ为
从而,由声功率与声强之间的关系,固体表面辐射的总声功率可表示为
| $W = \frac{1}{{{\rho _0}{c_0}}}\int_0^{2{\rm{ \mathsf{ π} }}} {\int_0^{\rm{ \mathsf{ π} }} {\overline {{p^{'2}}} } {r^2}} {\rm{sin}}\;\theta {\rm{d}}\theta {\rm{d}}\psi {\rm{ = }}\int_S {I\left( {\vec y} \right){\rm{d}}S\left( {\vec y} \right)} .$ | (5) |
其中
2) 四极子声源模型.Lighthill[12]方程主要解决气体流动本身产生的噪声问题.Proudman[13]和Lilley[14]由Lighthill方程出发,推导出四极子噪声源的声功率计算公式:
| ${P_{\rm{A}}} = \alpha {\rho _0}\left( {\frac{{{u^3}}}{l}} \right)\frac{{{u^5}}}{{c_0^5}}.$ | (6) |
式中:α为模型常量;u为湍流速度;l为湍流长度尺度.
将上式表示为湍动能k和湍流耗散率ε的表达式:
| ${P_{\rm{A}}} = {\alpha _\varepsilon }{\rho _0}\varepsilon M_t^5.$ | (7) |
式中:
计算模型包括截面形式为圆形、圆角方形(倒角率为1/5)和方形的3个柱体,模型高度为0.24 m,模型截面尺寸有0.03、0.034 3、0.04、0.048和0.06 m.计算中考虑了4种来流风速,分别为10、20、30和40 m/s.
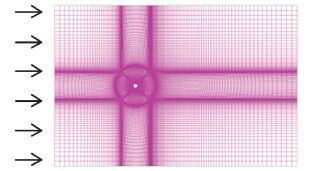
采用ANSYS ICEM建立准二维钝体绕流模型,忽略钝体的端部效应,但保留了钝体绕流的一些关键三维湍流因素.模型计算域在xoy平面的投影见图 1,钝体中心位于坐标原点(0, 0, 0),来流方向沿x轴正向.计算域入口和出口分别距离钝体中心20D和40D;左右边界距离钝体中心均为20D;计算域高度与计算模型相等,亦为0.24 m,因此上、下边界距离钝体中心均为0.12 m.计算域入口边界条件设置为速度入口(velocity-inlet),出口边界条件设置为压力出口(pressure-outlet);垂直于展向的两平面设置为对称边界,其余边界及钝体表面均设置为光滑、无滑移壁面.
|
图 1 计算域及其网格划分 Figure 1 Computational domain andthe grid configuration |
计算域全部采用分块非均匀结构化网格离散,并通过网格相关性分析确定合适的网格划分方案.以直径D=0.06 m、Re=160 000的圆形截面柱体为例,分别划分了网格总数为130万、250万及500万的3套网格,并比较这3套网格在计算收敛后相应监测点处的压力系数(Cp1和Cp2)、x方向速度(Vx3和Vx4),以及声功率级最大值(LA)、表面声功率级最大值(LS),如表 1所示.
| 表 1 不同网格方案的相关指标比较 Table 1 Comparisons of relevant indices for different schemes of grid configuration |
由表 1可知,当网格数达到250万时,计算值均基本保持不变,故采用此套网格作为后续计算的网格.计算域的网格划分如图 1所示,圆柱周围采用O型网格,第一层网格节点距圆柱壁面0.000 5 m,模型的周向、径向网格节点数为240×50;计算域在z轴方向的网格均匀划分,网格节点数为80.圆角方形及方形截面柱体的计算域横截面尺寸及网格划分方式与圆形截面柱体类似,不再赘述.
定常流场计算时,采用二阶迎风格式离散对流项,速度-压力耦合方程采用SIMPLE算法进行解耦.表面气动噪声源计算时,远场声速设置为340 m/s,参考声功率设置为10-12 W.
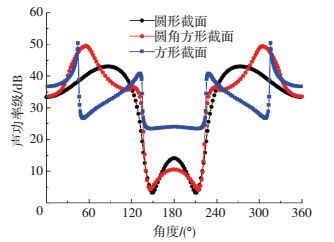
2 数值模拟结果分析 2.1 声功率级及表面声功率级声功率级和表面声功率级沿各钝体轴向的分布均基本不变,而沿周向的分布则变化显著,且不同截面形式具有不同的分布规律.图 2、3分别给出了不同截面形式的钝体在z=0截面处的声功率级和表面声功率级分布图.其中,0°对应前驻点,180°对应后驻点.无论是圆形、圆角方形还是方形截面钝体,其表面噪声源(包括四极子声源和偶极子声源)的主要区域均位于迎风面及侧面的角部,即气流发生分离、湍流运动比较剧烈的地方;不同截面形式钝体的最大噪声源位置有所不同,这是由于各截面的分离点位置不同导致的,且圆形截面钝体表面噪声源强度在气流分离点处的变化相较于圆角方形和方形截面钝体更为平缓;钝体背风面区域的噪声源强度均较小.比较声功率级和表面声功率级可知,钝体表面声功率级的分布情况和声功率级很相似,但峰值出现的角度及数值有所不同,具体分析见下文;在数值上声功率远小于表面声功率,也就是说,四极子噪声源对总噪声的贡献比偶极子噪声源的贡献要小得多,可以忽略.此外,由于各钝体的表面声功率级分布关于来流方向均呈现很好的对称性,因而下文仅分析钝体绕流0°~180°范围内的表面声功率级.
|
图 2 不同截面形式钝体的声功率级分布 Figure 2 Distribution of acoustic power level for bluff bodies with different cross-sections |
|
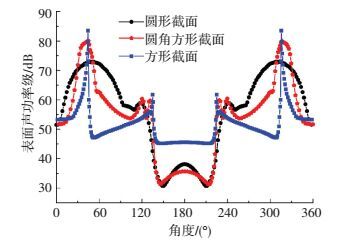
图 3 不同截面形式钝体的表面声功率级分布 Figure 3 Distribution of surface acoustic power level for bluff bodies with different cross-sections |
图 4、5分别给出了不同来流风速及不同截面尺寸时圆柱z=0截面的表面声功率级分布图,图 4的截面尺寸取为0.03 m,图 5中的来流风速取为10 m/s.由图可知,各模型的表面声功率级的分布形式基本相同,仅在数值上有所差别;来流风速越大,表面声功率级越大,40 m/s时的最大表面声功率级比10 m/s时大28.7 dB;截面尺寸越大,表面声功率级越小,总的来说,表面声功率级受截面尺寸的影响较小.此外,圆角方形截面钝体和方形截面钝体的表面声功率级也具有类似的分布规律,这里不再赘述.

|
图 4 不同来流风速下圆柱表面声功率级分布 Figure 4 Distribution of surface acoustic power level for cylinders under different oncoming wind speeds |

|
图 5 不同截面尺寸圆柱表面声功率级分布 Figure 5 Distribution of surface acoustic power level for cylinders with different characteristic sizes |
综上,下文仅分析钝体表面声功率级最大值随来流风速、钝体截面尺寸及截面形式的变化规律.
2.2 表面声功率级的影响参数分析1) 来流风速的影响.图 6给出了不同截面尺寸的圆柱表面声功率级最大值LS随来流风速lg U的变化曲线.由图可知,LS与lg U具有很好的线性关系.此外,圆角方形截面钝体和方形截面钝体也有类似的变化规律.对这些钝体的LS-lg U曲线进行线性拟合,可得到回归方程LS=klg U+b.表 2给出了各模型的拟合结果,其中R2为相关系数,反映了拟合程度的好坏.可以看出,相关系数均接近于1,说明拟合效果很好.

|
图 6 圆柱LS随来流风速lg U的变化 Figure 6 LS-lgU curves of cylinders |
| 表 2 LS-lg U的回归系数及相关系数 Table 2 The regression coefficients and correlation coefficients ofthe LS-lg U curves |
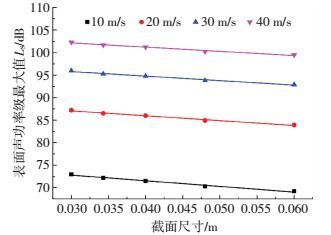
2) 截面尺寸的影响.图 7给出了4种来流风速下圆柱表面声功率级最大值LS随截面尺寸D的变化曲线.由图可知,对于10、20、30和40 m/s来流风速下的圆柱,当截面尺寸由0.03 m增至0.06 m时,柱体的LS分别降低了约4.2、3.2、3及2.8 dB,且LS与截面尺寸之间基本呈线性递减的变化规律.对于方形截面钝体和圆角方形截面钝体,其LS与截面尺寸的关系与圆柱类似.
|
图 7 圆柱LS随截面尺寸D的变化 Figure 7 LS-D curves of cylinders |
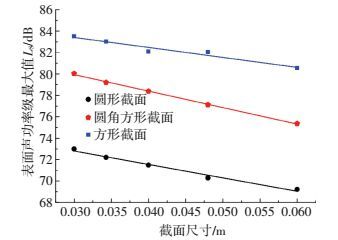
3) 截面形式的影响.图 8比较了不同截面形式钝体的表面声功率级最大值LS.限于篇幅,这里仅给出10 m/s来流风速的情况,其他来流风速与之类似,仅在数值上有所差别.由图可知,对于不同的截面尺寸(0.03~0.06 m),圆角方形截面钝体的LS比方形截面钝体降低了约3.5~5.2 dB,而圆形截面钝体的LS则比方形截面钝体降低了约10.1~11.8 dB.表面声功率级在数值上总体表现为方形截面>圆角方形截面>圆形截面,表明钝体外形趋近于流线型,其气动噪声源强度越低.
|
图 8 钝体LS随截面形式的变化 Figure 8 The maximum surface acoustic power level of bluff bodies with different cross-sections |
此外,随着来流风速的增加,圆形截面钝体、圆角方形截面钝体的LS相比方形截面钝体减小的数值和幅度均逐渐减小.当来流风速为40 m/s时,圆形截面钝体与圆角方形截面钝体的LS比方形截面钝体分别降低了约6.7~8.7 dB和0.9~1.9 dB.表明随着来流风速的增加,趋近于流线型的钝体的低噪声优势逐渐减弱.
2.3 表面声功率级数学预测模型由上述分析可知,钝体的表面声功率级最大值LS与来流风速lg U、截面尺寸D均呈线性关系,因此可由数值模拟结果分别拟合得到圆形、圆角方形(倒角率为1/5)和方形截面柱体的LS表达式:
| $\begin{array}{l} {L_{{\rm{S\_C}}}} = - 144.44D + 49.03{\rm{lg}}\;U + 27.13,\\ {L_{{\rm{S\_R}}}} = - 139.20D + 48.78{\rm{lg}}\;U + 35.02,\\ {L_{{\rm{S\_S}}}} = - 84.81D + 45.64{\rm{lg}}\;U + 39.98. \end{array}$ |
式中,LS_C、LS_R和LS_S分别为圆形、圆角方形和方形截面钝体的LS的预测值.
3 气动噪声源的影响机制探讨由1.2节中的叙述和式(7)可知,表面声功率级与湍动能k、湍流耗散率ε和壁面剪切应力等流场参数有关,而声功率级则可由k、ε计算得到.因此本节利用k、ε和壁面剪切应力等流场参数对气动噪声源的影响机制进行探讨.
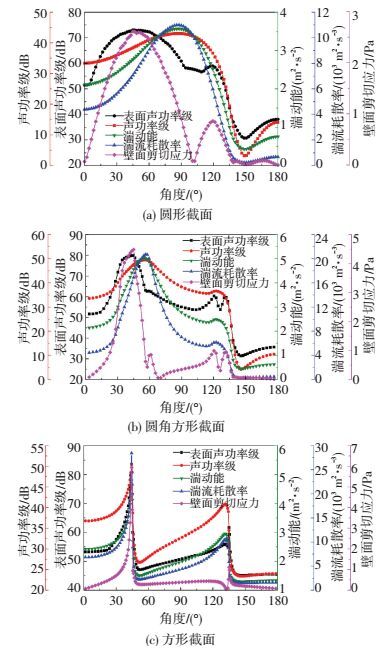
图 9给出了3种截面形式钝体在z=0高度处的气动噪声源强度(包括声功率级及表面声功率级)与流场参数(包括湍动能、湍流耗散率和壁面剪切应力)之间的关系对照图,各钝体的截面尺寸均取为0.03 m,来流风速为10 m/s.
|
图 9 气动噪声源强度与流场参数的关系对照图 Figure 9 Comparison of magnitude of aerodynamic noise sources and flow field parameters |
由图可知,圆形、圆角方形截面钝体的表面声功率级和壁面剪切应力在45°附近同时出现一个较高峰值,此外,圆形截面钝体在120°附近又同时出现一个较低峰值,而圆角方形截面钝体在120°和130°附近同时出现两个较低峰值.
圆形、圆角方形截面钝体的声功率级和湍动能、湍流耗散率的较高峰值角度也对应相等,但圆形截面钝体出现在85°附近,圆角方形截面钝体出现在55°附近.此外,圆形截面钝体的声功率级与湍动能、湍流耗散率又同时在150°附近出现一个较低值,而圆角方形截面钝体则在比145°略靠前的位置同时出现一个较低值;方形截面钝体的气动噪声源强度和3个流场参数均在45°附近同时出现一个较高峰值,而在135°附近又同时出现一个较低峰值.也就是说,钝体表面声功率级的分布和变化趋势与壁面剪切应力基本保持一致,声功率级的分布和变化趋势与湍动能和湍流耗散率基本保持一致,而对于不同截面形式的钝体而言,逆压梯度(剪切应力)和气流分离点位置的不同导致了它们各自的峰值角度有所不同.
综上,钝体的湍动能和湍流耗散率是影响其四极子声源的主要流场参数;钝体的壁面剪切应力是影响其偶极子声源的主要流场参数.
4 结论1) 钝体表面气动噪声源的主要区域位于迎风面及侧面角部,即气流发生分离、湍流运动比较剧烈的地方;圆形截面钝体表面噪声源强度在气流分离点处的变化相较于倒角率为1/5的圆角方形和方形截面钝体更为平缓;钝体背风面区域的噪声源强度均较小.
2) 声功率级的分布情况与表面声功率级类似,但四极子噪声源对总噪声的贡献比偶极子噪声源小得多.
3) 表面声功率级在数值上总体表现为方形截面>圆角方形截面(倒角率为1/5)>圆形截面,即外形趋近于流线型的钝体气动噪声源强度较低,但随着来流风速的增加,这种低噪声优势逐渐减弱.
4) 不同来流风速和截面尺寸时,钝体表面声功率级的分布形式基本相同,且表面声功率级最大值LS与来流风速lg U呈线性正相关,与截面尺寸D呈线性负相关.建立了不同截面形式钝体的表面声功率级预测模型,为工程结构中的声环境设计及气动噪声控制提供参考.
5) 钝体的湍动能和湍流耗散率是影响其四极子声源的主要流场参数;钝体的壁面剪切应力是影响其偶极子声源的主要流场参数.
| [1] |
刘加利. 高速列车气动噪声特性分析与降噪研究[D]. 成都: 西南交通大学, 2013: 2-4.
LIU Jiali. Study on characteristics analysis and control of aeroacoustics of high-speed trains [D]. Chengdu: Southwest Jiaotong University, 2013: 2-4. |
| [2] |
TALOTTE C, GAUTIER P E, THOMPSON D J, et al. Identification, modelling and reduction potential of railway noise sources: a critical survey[J].
Journal of Sound & Vibration, 2003, 267(3): 447-468.
DOI: 10.1016/S0022-460X(03)00707-7 |
| [3] |
赵磊. 大飞机噪声问题探讨[C]//中国航空学会2007年年会. 深圳: 中国航空学会, 2007.
ZHAO Lei.Discussion on the wind-induced noise of large aircrafts [C]//Annual Conference of Chinese Society of Aeronautics and Astronautics in 2007. Shenzhen: Chinese Society of Aeronautics and Astronautics, 2007. |
| [4] |
宁方立, 马尧, 王善景, 等. 飞机起落架气动噪声的数值计算方法[J].
机械工程学报, 2013, 49(8): 171-177.
NING Fangli, MA Yao, WANG Shanjing, et al. Numerical computational method for prediction aircraft landing gear noise[J]. Journal of Mechanical Engineering, 2013, 49(8): 171-177. DOI: 10.3901/JME.2013.08.171 |
| [5] |
CHOW L C, MAU K, REMY H. Landing gears and high lift devices airframe noise research [C]//8th AIAA/CEAS Aeroacoustics Conference & Exhibit. Breckenridge, Colorado:American Institute of Aeronautics and Astronautics, 2002:17-19.
|
| [6] |
LI Chunxi, LIN Qing, DING Xueliang, et al. Performance, aeroacoustics and feature extraction of an axial flow fan with abnormal blade angle[J].
Energy, 2016, 103: 322-339.
DOI: 10.1016/j.energy.2016.02.147 |
| [7] |
李春曦, 尹攀, 叶学民. 变工况下动叶安装角异常对轴流风机气动和噪声特性的影响[J].
动力工程学报, 2013, 33(7): 530-538.
LI Chunxi, YIN Pan, YE Xuemin. Influence of abnormal blade installation angle on aerodynamic and acoustic characteristics of axial flow fan under variable working conditions[J]. Journal of Chinese Society of Power Engineering, 2013, 33(7): 530-538. |
| [8] |
吴大转, 赵飞, 杨帅, 等. 叶片分布方式对微型风机气动噪声影响的数值研究[J].
风机技术, 2015(2): 20-25.
WU Dazhuan, ZHAO Fei, YANG Shuai, et al. Numerical simulation of the effect of blade distribution on the performance and aerodynamic noise of a mini fan[J]. Compressor Blower & Fan Technology, 2015(2): 20-25. DOI: 10.16492/j.fjjs.2015.02.152 |
| [9] |
吴晨晖, 杨兴林, 温华兵, 等. 大型船用轴流风机流场数值仿真及其气动噪声源特性研究[J].
船舶工程, 2016, 38(5): 28-33.
WU Chenhui, YANG Xinglin, WEN Huabing, et al. Numerical simulation of flow field and aerodynamic noise source characteristics of large marine axial flow fan[J]. Ship Engineering, 2016, 38(5): 28-33. DOI: 10.13788/j.cnki.cbgc.2016.05.028 |
| [10] |
SHIH T H, LIOU W W, SHABIR A, et al. A new eddy viscosity model for high Reynolds number turbulent flows model development and validation[J].
Computers & Fluids, 1995, 24(3): 227-238.
DOI: 10.1016/0045-7930(94)00032-T |
| [11] |
CURLE N. The influence of solid boundaries upon aerodynamic sound[J].
Proceedings of the Royal Society A, 1955, 231(1187): 505-514.
DOI: 10.1098/rspa.1955.0191 |
| [12] |
LIGHTHILL M J. On sound generated aerodynamically I: General theory[J].
Proceedings of the Royal Society of London, 1952, 211(1107): 564-587.
DOI: 10.1098/rspa.1952.0060 |
| [13] |
PROUDMAN I. The generation of noise by isotropic turbulence[J].
Proceedings of the Royal Society A, 1952, 214(1116): 119-132.
DOI: 10.1098/rspa.1952.0154 |
| [14] |
LILLEY G M. The radiated noise from isotropic turbulence revisited[J].
Theoretical and Computational Fluid Dynamics, 1994, 6(5): 281-301.
DOI: 10.1007/BF00311842 |
 2017, Vol. 49
2017, Vol. 49


