2. 北京科技大学 强震区轨道交通工程抗震研究北京市国际科技合作基地,北京 100083
2. Beijing International Cooperation Base for Science and Technology-Aseismic Research of the Rail Transit Engineering in the Strong Motion Area, University of Science and Technology Beijing, Beijing 100083, China
根据风机结构的自振频率可知,其动力特性与高度为60~160 m的高层建筑相似.因为在设计中不考虑舒适度,风振响应比一般结构更为显著.同时,由于叶片与来流风之间的相互作用以及控制特性等因素的影响,结构表现出明显的非线性.因此,需要结合结构的气弹特性和控制特性对风机的动力响应和风致疲劳进行分析.
目前,在风机结构的风致响应和风致疲劳分析中[1-7],通常将风场简化为平稳高斯随机过程,忽略风荷载高阶统计矩的影响.对于平坦均匀地形的边界层风场,高斯假设是恰当的.然而,实测数据表明,复杂地形的脉动风显示出明显的非高斯特性[8].同时,建筑结构和海岸工程在非高斯荷载作用下具有较大的极值响应并会加速疲劳破坏.
文献[9-10]在Hermite矩模型的基础上通过峰值因子法分别对单样本与多样本软化非高斯风荷载的极值进行了估计.文献[11]根据正交多项式和Hermite矩模型改进了非高斯风荷载的频域疲劳分析方法.在风荷载非高斯性对风机结构影响的研究方面,已有成果多集中于极值响应[12],欠缺对疲劳损伤的研究.特别是在考虑风机气弹特性和控制特性条件下疲劳裂纹形成寿命和裂纹扩展寿命两方面.
风机破坏多为叶片根部和塔架基础连接处[13],而复合材料的广泛使用提高了叶片强度和疲劳寿命,因此本文将控制截面限定于塔架基础连接处,但本文方法并不限于此.此外,本文主要分析非高斯风场对风机结构疲劳损伤的影响,故不考虑结构细部特征.
基于以上分析,本文在穿越模型基础上,模拟了多维相关平稳高斯、非高斯硬化和软化3种不同概率特性的风场,用于分析风场的非高斯性对风机结构疲劳损伤的影响.
1 风机与来流特性 1.1 风机结构基于NREL(national renewable energy laboratory)开发的基于气动耦合模型和多体动力的开源计算程序FAST(fatigue, aerodynamics, structures and turbulence)[14].以NREL轮毂高度90 m叶片直径126 m的5 MW三叶片陆上风机为例[15].该风机采用变速变桨距控制系统,额定风速11.4 m/s,额定转速12.1 r/min.
建立的风机模型共16个广义自由度,包括每个叶片的1阶、2阶摆振和1阶挥舞共9个自由度,塔体的1阶、2阶前后弯曲和1阶、2阶侧向弯曲共4个自由度,以及机舱偏航运动、发电机方位角变化、动力传动系统的转动变化3个自由度,风机塔底与地面刚接.模型的合理性及叶片、塔体的材料参数和气动参数可参见文献[15].
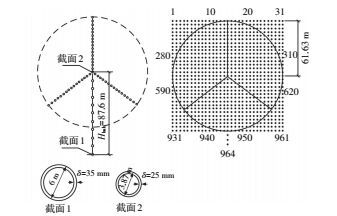
1.2 来流特性模拟的风场大小如图 1所示,按31×31划分网格,轮毂位于网格中心处.风机正常风速条件下按IEC 61400-1(international electro technical commission)规范中设计荷载条件(DLC)1.1和正常湍流模型(NTM)考虑载荷.
|
图 1 风机结构和风场示意 Figure 1 Sketch of wind turbine and wind field |
平均风速按指数律换算,地面粗糙度系数取α=0.2.脉动风速谱采用IEC规范中Kaimal谱模型.本文根据IEC规范,不考虑顺风向(u)、横风向(v)和垂直向(w)风速间的依赖性以及v和w风向风速的相关性,按指数相干函数模型仅考虑顺风向的相关性.脉动风速的标准差分别取σu=0.16(0.75uhub+5.6),σv=0.8σu和σw=0.5σu,uhub是轮毂高度处平均风速;湍流积分尺度分别取Lu=8.1Λu,Lv=2.7Λu和Lw=0.66Λu;湍流尺度系数Λu=0.7 min(30, Hhub).
2 风场模拟本文风场模拟在NREL风机风速时程开源模拟软件Turbsim[16]基础上进行二次开发.生成3个方向(u、v、w)的高斯风场后,将顺方向风速时程正则化,再根据Hermite矩模型和正交多项式模型[17]分别穿越成软化(峰度>3)、硬化(峰度<3)非高斯过程[18].
在风机运行状态,按单元宽度2 m/s将切入风速(3 m/s)到切出风速(25 m/s)划分为12个单元;在停机状态,考虑低于切入风速的1 m/s、2 m/s风速,共14种不同平均风速的硬化、软化和高斯风场.其中,软化过程的偏斜和峰度分别取0和4.5,硬化过程取0和1.5.为考虑由荷载样本引起的疲劳损伤不确定性,每个平均风速均采用相同的随机种子模拟,分别生成硬化、软化和高斯风速时程各50条.每条时程长度为630 s,时间间隔为0.05 s,频率上限为40 Hz.为消除启动瞬间的影响,从30 s后对结构动力响应进行分析.
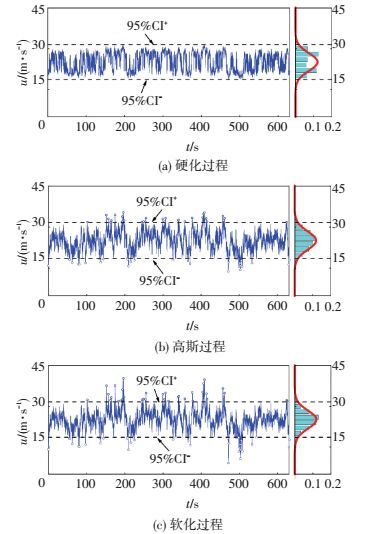
图 2所示为轮毂高度处平均风速25 m/s时,按谐波叠加法和穿越模型生成的硬化、高斯和软化风场.图中虚线表示均值加减1.96倍标准差(对于高斯分布即95%置信度区间);柱状图为模拟风速时程的概率密度函数(PDF),实线为相同均值和方差条件下的高斯分布PDF.由图可知,软化和硬化风场均表现出明显的非高斯性,在相同目标条件下,高斯风场的极值大小及其数量介于硬化和软化过程之间.
|
图 2 轮毂高度处风速时程 Figure 2 Simulated wind speed time histories at the hub height |
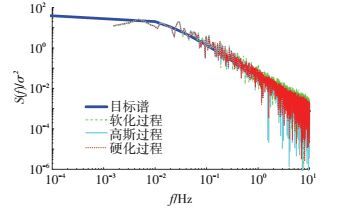
图 3比较了目标谱与生成风速时程的模拟谱,结果表明3种不同概率特性风场的PSD与目标谱均吻合较好.
|
图 3 模拟谱与目标谱比较 Figure 3 Comparison between simulated spectrum and target spectrum |
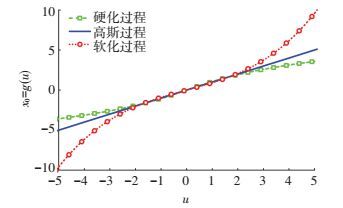
如图 4所示为图 2中非高斯过程的由Hermite矩模型和正交多项式模型计算得到的穿越函数.其中,软化过程与高斯过程、硬化过程与高斯过程的相关系数分别为0.99和0.96,即穿越模型保持了3种荷载的相关性.
|
图 4 非高斯穿越模型 Figure 4 Translation models of non-Gaussian processes |
本文采用基于耦合气动模型的FAST程序计算结构的动力响应.在动力响应分析中,采用叶素动量理论考虑叶片尾流模型,按Beddoes-Leishman模型考虑叶片的气动效应.由于面内弯曲应力(Sb)远大于其他应力,因此本文仅对弯曲应力的动力响应和风致疲劳损伤进行分析.
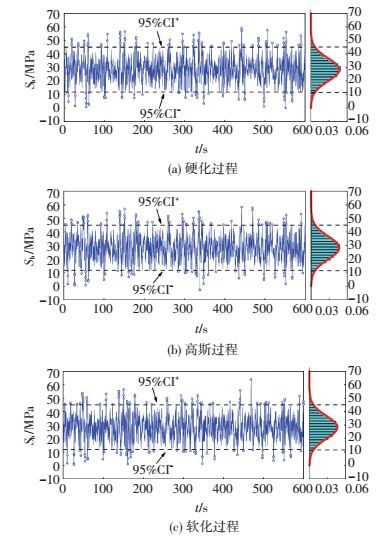
如图 5所示为轮毂高度处平均风速25 m/s时,风机结构在3种不同概率特性风场作用下,控制截面面内弯曲应力时程.可以看出,风机结构应力响应的非高斯性较风场的非高斯性减弱.
|
图 5 风荷载作用下控制截面面内弯曲应力时程 Figure 5 Time histories of in-plane bending stress of the critical section |
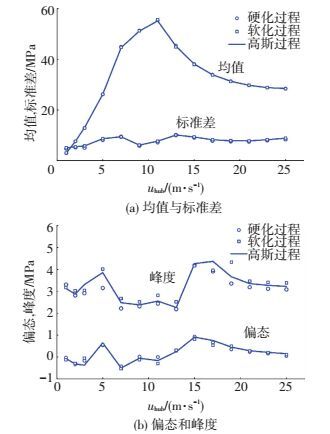
如图 6所示为高斯、软化和硬化风场各50条分别计算得到的应力响应前四阶统计矩的平均值随风速的变化.由图 6可知,高斯、非高斯风场作用下应力响应均值的平均值近似相等,且在额定风速之前随平均风速的增大而快速增大;在额定风速之后,由于桨距控制,平均值随风速的增大逐渐减小.与均值类似,不同概率特性风场作用下,应力响应的标准差和偏态的平均值也近似相等,但受控制系统影响,平均值随风速变化不明显.需要指出的是,峰度的平均值有所不同,软化、高斯和硬化风场作用下峰度的平均值依次减小,但随风速变化的整体趋势一致.在额定风速之前,即使是高斯风场作用下的应力响应也表现出明显的硬化特性;在额定风速之后,峰度的平均值呈上升趋势表现出软化特性.
|
图 6 风荷载作用下控制截面面内弯曲应力的时域特性 Figure 6 First four statistical moments of in-plane bending stress of the critical section with mean wind speeds |
此外,在均值和方差近似相等的条件下,软化、高斯和硬化风场作用下, 对应不同风速的50个应力时程的最大值的离散程度依次减小.
4 裂纹形成寿命结构的疲劳寿命通常由裂纹形成寿命(Ti)和裂纹扩展寿命(Tp)两部分组成.对于裂纹形成寿命,本文采用线性损伤累积理论,并考虑由结构和荷载两方面不确定性引起的裂纹形成寿命的不确定性[19].同时,将结构的不确定性限定于S-N曲线参数;对外荷载的不确定性,仅考虑由不同应力样本引起的损伤不确定性,并将疲劳损伤的概率分布近似为高斯分布.
4.1 考虑荷载不确定性的裂纹形成寿命根据雨流计数法,统计得到应力幅值(Sri)和相应幅值的频率(fi)后,由P-M准则,将等效应力幅表示为
| $ S_{{\rm{reff}}}^0 = {\left( {\sum\limits_i {{f_i}S_{{\rm{r}}i}^3} } \right)^{1/3}}. $ | (1) |
为考虑应力均值影响,按Goodman准则将零均值应力过程(Sreff0)转化为均值为Sm的应力过程.
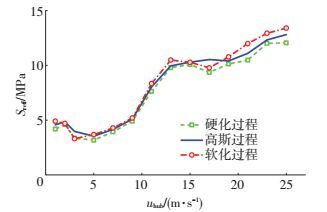
图 7所示为高斯、非高斯风场作用下风机结构控制截面处的等效应力幅(Sreff).总体而言,软化、高斯和硬化过程的等效应力幅依次减小,但个别风速处与整体趋势并不完全一致.同时,在额定风速之前,等效应力幅随平均风速的增大而增大;在额定风速之后,由于控制系统等因素,等效应力幅在一段范围内保持相对稳定,并在平均风速大于20 m/s后呈缓慢上升趋势.此外,当风速低于切入风速(3 m/s)时,风机未正常发电,风力未有效转化为风能,故等效应力幅较切入风速时大.
|
图 7 等效应力幅随平均风速的变化 Figure 7 Equivalent stress amplitudes with different mean wind speeds |
在计算风机控制截面的疲劳寿命时,等效应力幅作用下应力循环的次数表示为
| $ {N_{\rm{f}}} = AS_{{\rm{reff}}}^{ - m}, $ | (2) |
式中A和m是S-N曲线参数.按美国公路桥梁设计规范(AASHTO LRFD bridge design specifications)中E类曲线取值,即m=3.0和A=36.1×1010 MPa3.为考虑疲劳极限,应力幅阀值取31 MPa,即应力幅值Sri<15.5 MPa时不引起疲劳损伤.
由P-M准则可知,时间T内控制截面处的疲劳损伤可表示为
| $ D = \frac{{v_0^ + \cdot T}}{{{N_{\rm{f}}}}}, $ | (3) |
式中v0+是单位时间内的平均穿越率.
图 8所示为控制截面处弯曲应力的平均穿越率随风速的变化情况.3种风场作用下的平均穿越率v0+基本相同.在风速大于切入风速小于额定风速范围内,v0+随平均风速增大而迅速减小;达到额定风速后,受控制系统影响,v0+基本保持不变.

|
图 8 平均穿越率随平均风速的变化 Figure 8 Mean crossing rates with different mean wind speeds |
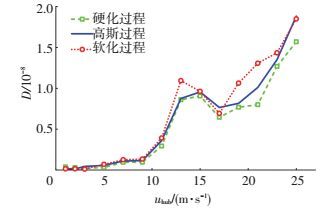
图 9所示为不同平均风速下的疲劳损伤率.由于疲劳损伤是等效应力幅的高次非线性方程,因此3种风场作用下的疲劳损伤率差别较等效应力幅明显(图 7),但整体趋势与等效应力幅一致.同时,由于考虑疲劳极限影响,当风速低于切入风速时疲劳损伤率较小.在风速达到额定风速后的一段范围内,损伤率保持相对稳定,风速超过20 m/s后快速增长.
|
图 9 疲劳损伤率随平均风速的变化 Figure 9 Fatigue damage rates with different mean wind speeds |
根据中心极限定理,通常认为疲劳损伤服从高斯分布[20].因此,风机结构的疲劳寿命期望(E[Ti])和方差(σ2[Ti])分别表示为[21]:
| $ \begin{array}{l} E\left[ {{T_{\rm{i}}}} \right] = \frac{1}{{{\mu _{\rm{D}}}}}\left[ {1 + \frac{{\sigma _{\rm{D}}^2}}{{2{\mu _{\rm{D}}}}}} \right]T,\\ {\sigma ^2}\left[ {{T_i}} \right] = \frac{{\sigma _{\rm{D}}^2}}{{\mu _{\rm{D}}^3}}\left( {1 + 1.25\frac{{\sigma _{\rm{D}}^2}}{{{\mu _{\rm{D}}}}}} \right){T^2}. \end{array} $ | (4) |
式中μD和σD是时间T内控制点处的疲劳损伤期望和标准差,分别表示为:
| $ {\mu _{\rm{D}}} = \int {{\mu _{\rm{D}}}\left( {{u_{{\rm{ave}}}}} \right)f\left( {{u_{{\rm{ave}}}}} \right){\rm{d}}{u_{{\rm{ave}}}}} ,{\sigma _{\rm{D}}} = \int {{\sigma _{\rm{D}}}\left( {{u_{{\rm{ave}}}}} \right)f\left( {{u_{{\rm{ave}}}}} \right){\rm{d}}{u_{{\rm{ave}}}}} . $ | (5) |
式中:uave是年平均风速;f(uave)是年平均风速的PDF,按Rayleigh分布对平均风速进行简化.
图 10所示为不同年平均风速条件下的疲劳裂纹形成寿命.在应力均值和方差相同的条件下(图 6),当年平均风速uave较小时,由于软化风场作用下应力响应的峰度系数较大,应力集中在均值附近,因此低于应力幅阀值的应力循环相对较多,而在考虑疲劳极限时,这些应力循环不造成疲劳损伤累积,所以软化风场作用下的裂纹形成寿命与高斯风场作用下差别不大.在uave增大过程中,软化风场的应力幅值也逐渐增大,此前低于应力幅阀值的应力循环幅值逐渐大于应力幅阀值,因此疲劳损伤累积较其他两种风场大,疲劳裂纹形成寿命较小.分析可知,在年平均风速较大地区建立风机时,需要考虑风场的非高斯特性.

|
图 10 不同年平均风速条件下的疲劳裂纹形成寿命 Figure 10 Fatigue crack initiation life with different annual mean wind speeds |
表 1所示为高斯、非高斯风场作用下控制截面面内弯曲应力引起的裂纹形成寿命的期望和标准差.由表可知,在年平均风速为5 m/s时,风场的软化特性对裂纹形成寿命影响较小;相较于高斯风场,硬化风场引起的裂纹形成寿命显著提高.随着年平均风速的增大,风场的非高斯性对裂纹形成寿命的影响逐渐明显.此外,由于软化、高斯和硬化风场作用下响应的峰度系数依次减小,在均值和方差相同的情况下,峰度较大的风场下的应力较集中于应力均值附近,应力幅值的离散程度较小,故疲劳损伤的标准差较小.在疲劳损伤分析中,时间t内的应力循环次数为N(t)时,损伤标准差(σD(t))与均值(μD(t))的比值按[N(t)]-1/2衰减[22],因此由风场样本引起的寿命标准差远小于寿命均值,可忽略荷载样本的不确定性对疲劳损伤的影响.
| 表 1 不同年平均风速条件下,3种风场作用下裂纹形成寿命的期望和标准差 Table 1 Mean and standard deviation of crack initiation life under three types of wind loads with different annual mean wind speeds |
S-N曲线参数具有很强的离散性,设计规范中通常选取存活率为95%以上的S-N曲线进行设计,严重低估了裂纹形成寿命.
现有研究表明,S-N曲线参数A可近似认为服从对数高斯分布[23].本文按AASHTO规范中E类曲线取值,即μA=65.9×1010 MPa3,δA=0.26.
在P-M准则中,认为疲劳损伤D累积到界限Δ时,控制截面产生裂纹,工程中通常取Δ=1.文献[23]指出需要考虑累积界限Δ的不确定性,并认为Δ服从对数高斯分布,取μΔ=1和δΔ=0.3.考虑累积界限的不确定性时,控制截面产生裂纹时的应力循环次数表示为
| $ {N_{\rm{c}}} = \frac{{A\Delta }}{{S_{{\rm{reff}}}^3}}, $ | (6) |
裂纹形成寿命的失效概率定义为
| $ {P_{\rm{f}}} = 1 - \mathit{\Phi }\left( \beta \right), $ | (7) |
式中Φ(·)是标准高斯分布的概率分布函数(CDF);β是可靠性指数,表示为
| $ \beta = \frac{{\left( {{\lambda _\Delta } + {\lambda _A}} \right) - 3\ln {S_{{\rm{reff}}}} - \ln N}}{{\sqrt {\zeta _\Delta ^2 + \zeta _A^2} }}, $ | (8) |
其中λΔ、λA、ζΔ和ζA分别表示为:
| $ \begin{array}{l} {\lambda _A} = \ln {\mu _A} - \frac{{\zeta _A^2}}{2},{\lambda _\Delta } = \ln {\mu _\Delta } - \frac{{\zeta _\Delta ^2}}{2};\\ {\zeta _A} = \sqrt {\ln \left( {1 + \delta _A^2} \right)} ,{\zeta _\Delta } = \sqrt {\ln \left( {1 + \delta _\Delta ^2} \right)} . \end{array} $ | (9) |
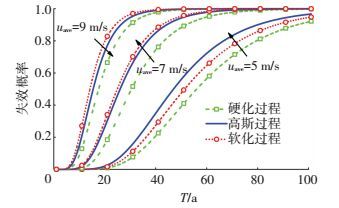
图 11所示为不同年平均风速条件下计算得到的对应不同使用年限裂纹形成的失效概率.与图 10类似,当年平均风速uave较小时,疲劳损伤累积较小.在uave增大过程中,软化风场作用下的疲劳损伤逐渐增大.因此,在年平均风速较大地区建立风机需要考虑风场的非高斯性.
|
图 11 不同年平均风速条件下,不同使用年限裂纹形成的失效概率 Figure 11 Failure probability of crack initiation life with different service lives with different annual mean wind speeds |
通常依据裂纹扩展速率将裂纹扩展分为失稳扩展和亚临界扩展两阶段.根据线性断裂理论,当应力强度因子幅度ΔK小于其临界值KIC时,疲劳裂纹扩展应力循环次数Nif可表示为
| $ {N_{{\rm{if}}}} = \frac{{a_{\rm{f}}^{1 - m/2} - a_{\rm{i}}^{1 - m/2}}}{{C{{\left( {F\Delta S\sqrt {\rm{ \mathit{ π} }} } \right)}^m} \cdot \left( {1 - m/2} \right)}}, $ | (10) |
式中:af和ai分别表示临界裂纹尺寸和初始裂纹长度;通常认为初始裂纹贯穿结构壁厚t,即2ai=2t;ΔS是有效应力范围,取ΔS=Sreff;F是裂纹几何形状和尺寸的无量纲参数,当裂纹长度与构件宽度比α≤0.4时,取F=1.12[24].
根据英国标准委员会颁布的《金属结构中缺陷验收评定方法导则》(BS 7910)中1A等级,临界裂纹尺寸表示为
| $ {a_{\rm{f}}} = {a_{\rm{c}}} = \frac{1}{{\rm{ \mathit{ π} }}}{\left( {\frac{{0.707{K_{{\rm{IC}}}}}}{{{S_{{\rm{t}},\max }}}}} \right)^2}, $ | (11) |
式中KIC是应力强度因子临界值,由夏比冲击实验(CVN)确定;St, max是塔体控制截面处的最大拉应力,St, max={KSreff/2-P/A]+σy};K表示应力集中系数,对于角焊缝连接取1.5;P/A表示结构自重除以截面面积;σy表示材料的屈服强度,本文选取的是ASTM A36型钢材.
由平均风速的PDF和应力循环次数可得裂纹扩展寿命,表示为
| $ {T_{\rm{P}}} = \frac{1}{{\int {\hat D\left( {{u_{{\rm{ave}}}}} \right)f\left( {{u_{{\rm{ave}}}}} \right){\rm{d}}{u_{{\rm{ave}}}}} }}, $ | (12) |
式中
| $ \hat D\left( {{u_{{\rm{ave}}}}} \right) = \frac{{v_0^ + }}{{{N_{{\rm{if}}}}}} \cdot T. $ | (13) |
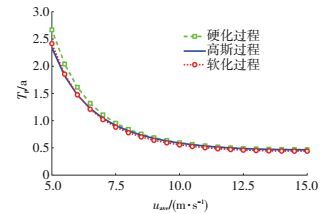
图 12所示为控制截面疲劳裂纹扩展寿命随年平均风速的变化曲线.由图可知,3种风场作用下裂纹扩展寿命差别较小,这主要是由于计算最大拉应力St, max时考虑了材料屈服强度σy,而σy远大于等效应力幅Sreff.随着年平均风速的增大,风场的非高斯特性逐渐对裂纹扩展寿命产生影响,但影响并不明显,因此可忽略风场的非高斯性对裂纹扩展寿命的影响.此外,相较于裂纹形成寿命,裂纹扩展寿命相对较小,可将裂纹扩展寿命作为安全储备.
|
图 12 不同年平均风速条件下的裂纹扩展寿命 Figure 12 Fatigue crack propagation life with different annual mean wind speeds |
现有研究集中于高斯风场作用下的风机结构疲劳损伤,然而在复杂地貌下风荷载通常表现出明显的非高斯特性.针对这一问题,本文基于穿越模型,通过Monte Carlo模拟生成了硬化、软化非高斯和高斯3种不同概率特性的风场.研究了风场的非高斯性对风机疲劳损伤的影响.在考虑叶片与来流间的气弹效应及叶片与塔体相互作用的条件下,根据多体动力有限元,计算出控制截面处的面内弯曲应力,并对响应的时域特性进行了分析.将结构使用寿命分为疲劳裂纹形成寿命和疲劳裂纹扩展寿命,分别采用线性损伤累积理论和线性裂纹扩展理论对3种风场作用下控制截面处的疲劳寿命进行了详细讨论,并考虑了荷载和材料两种不确定性对裂纹形成寿命的影响,得到以下几点结论:
1) 软化非高斯、高斯和硬化非高斯3种不同概率特性风场作用下风机结构动力响应最大值依次减小,且响应的非高斯性较风场的非高斯性减弱.
2) 在裂纹形成阶段,风荷载的非高斯性对风机结构疲劳损伤的影响随平均风速的增大而变得显著.在年平均风速较低地区,风场的非高斯性对裂纹形成寿命的影响较小;但随着年平均风速的增大,其影响逐渐明显.当年平均风速为7 m/s和9 m/s时,相较于高斯过程,软化非高斯风场作用下的裂纹形成寿命减小约10%.因此,在年平均风速较大地区,需要考虑风场的软化特性对疲劳裂纹形成寿命的影响.
3) 在裂纹扩展阶段,风场的非高斯性对裂纹扩展寿命影响较小,相较于高斯过程,软化过程的裂纹扩展寿命平均减小约4%.因此,在裂纹扩展阶段可不考虑荷载的非高斯性,并将裂纹扩展寿命作为疲劳寿命的安全储备.
| [1] |
MARINO E, GIUSTI A, MANUEL L. Offshore wind turbine fatigue loads: The influence of alternative wave modeling for different turbulent and mean winds[J].
Renewable Energy, 2017, 102(Part A): 157-169.
DOI: 10.1016/j.renene.2016.10.023 |
| [2] |
REPETTO M P, TORRIELLI A. Long term simulation of wind-induced fatigue loadings[J].
Engineering Structures, 2017, 132: 551-561.
DOI: 10.1016/j.engstruct.2016.11.057 |
| [3] |
YETER B, GARBATOV Y, GUEDES SOARES C. Fatigue damage assessment of fixed offshore wind turbine tripod support structures[J].
Engineering Structures, 2015, 101: 518-528.
DOI: 10.1016/j.engstruct.2015.07.038 |
| [4] |
DO T, VAN DE LINDT J, MAHMOUD H. Fatigue life fragilities and performance-based design of wind turbine tower base connections[J].
Journal of Structural Engineering, 2014, 141(7): 4014183.
DOI: 10.1061/(ASCE)ST.1943-541X.0001150 |
| [5] |
QUILLIGAN A, O CONNOR A, PAKRASHI V. Fragility analysis of steel and concrete wind turbine towers[J].
Engineering Structures, 2012, 36: 270-282.
DOI: 10.1016/j.engstruct.2011.12.013 |
| [6] |
DONG W, MOAN T, GAO Z. Long-term fatigue analysis of multi-planar tubular joints for jacket-type offshore wind turbine in time domain[J].
Engineering Structures, 2011, 33(6): 2002-2014.
DOI: 10.1016/j.engstruct.2011.02.037 |
| [7] |
VELDKAMP D. A probabilistic evaluation of wind turbine fatigue design rules[J].
Wind Energy, 2008, 11(6): 655-672.
DOI: 10.1002/we.287 |
| [8] |
FRAGOULIS A, FRAGOULIS A. The complex terrain wind environment and its effects on the power output and loading of wind turbines[C]// ASME1997-Wind Energy Symposium. America: American Institute of Aeronautics and Astronautics, 1997: 33-40.
|
| [9] |
KWON D, KAREEM A. Peak Factors for Non-Gaussian Load Effects Revisited[J].
Journal of Structural Engineering, 2011, 137(12): 1611-1619.
DOI: 10.1061/(ASCE)ST.1943-541X.0000412 |
| [10] |
YANG Qingshan, TIAN Yuji. A model of probability density function of non-Gaussian wind pressure with multiple samples[J].
Journal of Wind Engineering and Industrial Aerodynamics, 2015, 140: 67-78.
DOI: 10.1016/j.jweia.2014.11.005 |
| [11] |
DING Jie, CHEN Xinzhong. Fatigue damage evaluation of broad-band Gaussian and non-Gaussian wind load effects by a spectral method[J].
Probabilistic Engineering Mechanics, 2015, 41: 139-154.
DOI: 10.1016/j.probengmech.2015.06.005 |
| [12] |
GONG Kuangmin, CHEN Xinzhong. Influence of non-Gaussian wind characteristics on wind turbine extreme response[J].
Engineering Structures, 2014, 59: 727-744.
DOI: 10.1016/j.engstruct.2013.11.029 |
| [13] |
CHOU Juisheng, TU Wanting. Failure analysis and risk management of a collapsed large wind turbine tower[J].
Engineering Failure Analysis, 2011, 18(1): 295-313.
DOI: 10.1016/j.engfailanal.2010.09.008 |
| [14] |
JONKMAN B, JONKMAN J. FAST user's guide[R]. America: National Renewable Energy Laboratory, 2016.
|
| [15] |
JONKMAN J M, BUTTERFIELD S, MUSIAL W, et al. Definition of a 5 MW reference wind turbine for offshore system development[R].America: National Renewable Energy Laboratory, 2009.
|
| [16] |
JONKMAN B. TurbSim user's guide[R].America: National Renewable Energy Laboratory, 2016.
|
| [17] |
DING Jie, CHEN Xinzhong. Moment-based translation model for hardening non-Gaussian response processes[J].
Journal of Engineering Mechanics, 2015, 142(2): 6015006.
DOI: 10.1061/(ASCE)EM.1943-7889.0000986 |
| [18] |
SHIELDS M D, DEODATIS G. A simple and efficient methodology to approximate a general non-Gaussian stationary stochastic vector process by a translation process with applications in wind velocity simulation[J].
Probabilistic Engineering Mechanics, 2013, 31: 19-29.
DOI: 10.1016/j.probengmech.2012.10.003 |
| [19] |
BENGTSSON A, RYCHLIK I. Uncertainty in fatigue life prediction of structures subject to Gaussian loads[J].
Probabilistic Engineering Mechanics, 2009, 24(2): 224-235.
DOI: 10.1016/j.probengmech.2008.06.004 |
| [20] |
LOW Y M. Variance of the fatigue damage due to a Gaussian narrowband process[J].
Structural Safety, 2012, 34(1): 381-389.
DOI: 10.1016/j.strusafe.2011.09.001 |
| [21] |
DING Jie, CHEN Xinzhong, ZUO Delong, et al. Fatigue life assessment of traffic-signal support structures from an analytical approach and long-term vibration monitoring data[J].
Journal of Structural Engineering, 2016: 4016017.
DOI: 10.1061/(ASCE)ST.1943-541X.0001475 |
| [22] |
LUTES L D, SARKANI S.
Randomvibrations: analysis of structural and mechanical systems[M]. Burlington: Elsevier Inc, 2004.
|
| [23] |
CHUNG H, MANUEL L, FRANK K H. Optimal inspection of fracture-critical steel trapezoidal girders[R].America: Center for Transportation Research, University of Texas at Austin, 2003.
|
| [24] |
DOWLING N E.
Mechanical behavior of materials[M]. England: Angshuman Chakraborty, 2007.
|
 2017, Vol. 49
2017, Vol. 49


