2. 高速铁路建造技术国家工程实验室(中南大学), 长沙 410075
2. National Engineering Laboratory for High-speed Railway Construction (Central South University), Changsha 410075, China
针对超高层建筑的气动优化措施大体可以分为被动控制和主动控制[1].被动控制最常见的是结构物的外形优化, 如:采用倒角、圆角、凹角或角部扰流片, 柱体贯穿开洞, 沿高度改变建筑横截面面积, 增加棱柱体顶面棱边和侧面螺旋线的数量[2-7].相比于被动控制, 主动控制方法以其可控性更能适用于复杂的风环境.其中吹、吸气方法是常见的主动控制措施之一.文献[8]在高宽比H/d为6的高层建筑模型不同高度上开设吸气孔, 研究了不同风向角下模型侧面和背面定常吸气的控制效果.实验发现侧面吸气比背面吸气效果更好, 且开孔距流动分离点越近, 控制效果越好.文献[9-11]通过数值模拟研究了高层建筑侧面全高和分段的吸、吹气控制, 发现气流角度、开孔位置和开孔宽度对控制效果都有影响, 但主要受无量纲的吸气量系数控制.从能耗和折减效率的角度分析, 发现吸、吹气有不同的适用范围, 且分段控制效果不如全高控制.文献[12-13]进一步探讨了被动控制和主动控制相结合的方法, 研究了方形、Y形截面形式、锥台形式和带切角或凹角形式的高层建筑模型在0°至45°风向角下通过两侧吸气的控制效果.实验发现, 除锥台模型外, 其他各吸气模型对横风向脉动力都有很好的抑制效果.
有研究发现, 有限长柱体顶部形成下扫流对其气动力有很大影响[14-16], 但是能否通过控制下扫流实现对高层建筑气动力的控制仍有待进一步验证.本文通过风洞试验, 在正方形截面的高层建筑简化模型顶部施加定常吸气, 系统地研究了吸气对气动力的影响规律, 并通过流动可视化、流场测量等方法对顶部吸气控制的机理进行了探讨.
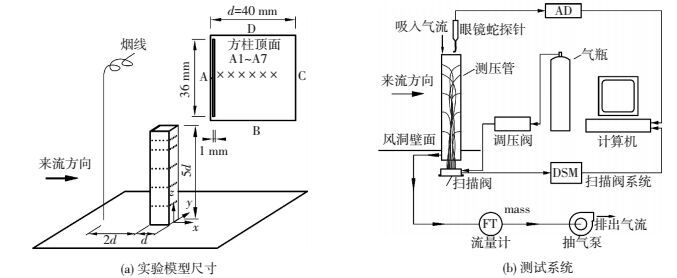
1 实验介绍所有试验在一直流式风洞内进行, 其实验段截面尺寸为450 mm×450 mm, 风速范围0~40 m/s, 湍流度小于0.5%.被测高层建筑简化为一正方形截面棱柱, 宽d=40 mm, 高宽比H/d=5.模型由韧性类ABS树脂经3D打印制成, 刚度及表面光滑度都能满足实验要求.安装模型前, 对风洞壁面边界层进行标定, 其厚度约为0.4d, 即模型0.4d以上高度都处于均匀来流中. 图 1(a)给出了模型示意图与坐标系的定义.坐标系原点为方柱底面中心.模型顶面迎风侧距边缘1 mm处开设有一宽1 mm长36 mm的吸气细缝.模型底部的出气管与放置在风洞外的抽气泵相连, 并可通过流量计监测吸气流量, 见图 1(b).在z* = 1, 2, 3, 4和4.5等(z*= h/d, h为测点高度, d为方柱宽度)不同高度上, 布置五层测压孔.每层各个面的测压点为5个, 沿柱体表面均匀布置.测压试验使用美国Scannivalve公司ZOC33/64PxX2高频压力扫描阀进行测量, 测压试验采样频率为625 Hz, 采样时间32 s, 测压系统见图 1(b).实验中自由来流风速U∞ = 9.8 m/s, 基于d与U∞的Re=2.74×104.通过流量计监测吸气的体积流量, 并依据吸气狭缝面积, 估算狭缝吸气速度U, 定义吸气系数Q=U/U∞.试验研究了Q=0~4范围内顶部狭缝吸气对模型气动力与顶部剪切流的影响规律.
|
图 1 实验装置 Figure 1 Experimental setups |
模型表面各测压点时均压力系数Cpi和脉动风压系数C′pi为:
| ${C_{pi}} = \frac{{\overline {\left( {{p_i} - {p_\infty }} \right)} }}{{0.5\rho U_\infty ^2}},$ | (1) |
| ${{C'}_{pi}} = \frac{{{{p'}_i}}}{{0.5\rho U_\infty ^2}}.$ | (2) |
式中: pi表示各测点风压, p∞为风洞静压, ρ为空气密度, p′i为测压点脉动风压的均方根值(RMS值).根据测点代表的面积, 可计算得到模型总体所受阻力系数Cd, whole, 脉动阻力系数C′d, whole和脉动升力系数C′l, whole.
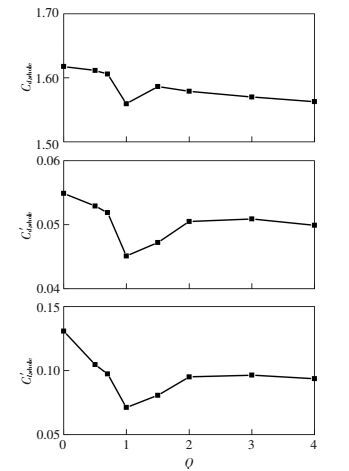
2 结果分析与讨论 2.1 气动力图 2给出了吸气系数Q从0到4时, Cd, whole、C′d, whole和C′l, whole的变化规律.由图 2可以看出, 顶部狭缝定常吸气对模型气动力有明显的影响.在Q=0~1.0之间, Cd, whole、C′d, whole和C′l, whole随着Q增大而减小, 且在Q= 1附近达到最小值.随着Q继续增大, 三者均有所增大.当Q>2.0后, Cd, whole、C′d, whole和C′l, whole基本趋于稳定.显然, 最优效果出现在Q=1时, 相对于无控制工况(Q=0), Cd, whole、C′d, whole和C′l, whole分别减小了3.60%, 17.85%和45.57%.
|
图 2 方柱整体受到的Cd, whole、C′d, whole和C′l, whole随Q增长的变化曲线 Figure 2 Effects of Q on the Cd, whole, C′d, whole and C′l, whole of the tested cylinder |
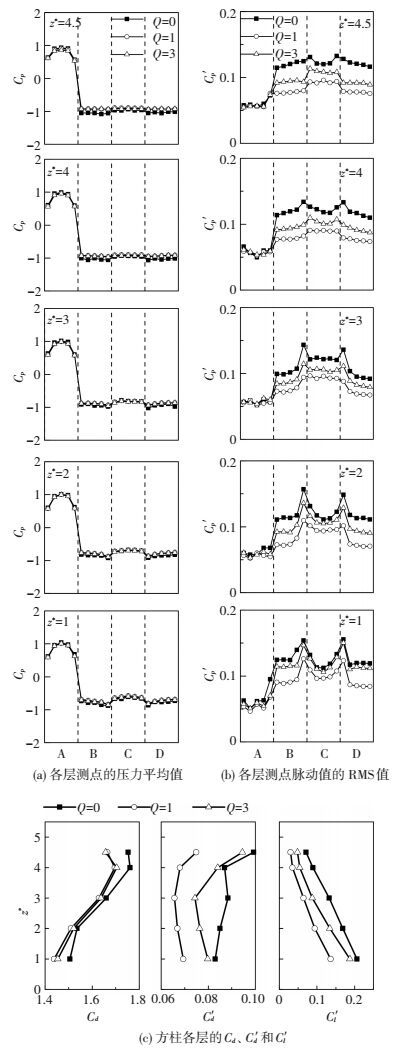
图 3给出了Q=0, 1和3条件下, 方柱不同高度处Cpi和C′pi分布情况(图 3(a)、(b)), 以及各高度对应的局部气动力系数(图 3(c)).由图 3(a)、(b)可以看出, 顶部吸气对模型迎风面的平均风压与脉动风压影响都不大.相对于无控制情况, Q=1和3时模型背面与侧面所有高度上的Cpi略有升高, 但变化幅度较小.这也是为何模型时均阻力系数在顶部吸气控制下最大仅减小3.6%的原因.如图 3(b)所示, 顶部吸气对模型所有高度上的脉动风压C′pi都有显著的影响.显然, 当Q=1时, 模型所有高度上的C′pi都到达了最小值, 而当Q进一步加大到3时, C′pi又有所增大.
|
图 3 Q=0、1和3时方柱气动力沿展向的分布 Figure 3 Distribution of the aerodynamic forces at different spanwise positions with Q=0, 1 and 3 |
图 3(c)给出的是模型不同高度上的局部气动力系数Cd、C′d和C′l.顶部吸气对Cd的影响在z*= 4和4.5附近较为明显, 吸气后都减小约6%;而模型下半部分Cd变化相对较小.与阻力系数Cd相比, 顶部吸气对C′d和C′l 的影响更为显著. Q=1时, z* =4.5、4、3、2和1等不同高度处, C′d分别减小了25%、22%、26%、21%和16%, 而C′l分别减小了58%、61%、52%、44%和34%.可以看出顶部的吸气对模型顶部附近的C′d和C′l 抑制较为显著, 随着向模型底部靠近, 这一抑制作用略有减小.但即使在z* = 1的高度上, C′d和C′l仍分别减小了16%和34%. Q=3时, 各高度处C′d和C′l的控制效果仍非常显著, 但已明显弱于Q=1时的脉动力抑制效果.总的来看, 模型顶部狭缝吸气这一局部控制措施, 对整个模型高度上的C′d和C′l均有显著的抑制作用.
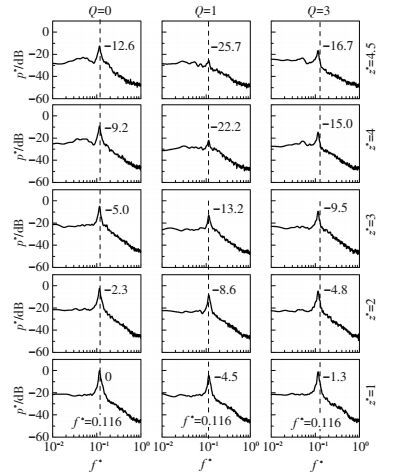
图 4给出了模型各高度上局部的升力系数自功率谱.为方便对比, 所有工况下各层的功率谱均以无控制时z*=1的谱峰值强度作为参考值, 按式(3)无量纲化为dB.频率则以来流速度U∞和方柱宽度d按式(4)无量纲.
|
图 4 方柱在Q=0、1和3时的各层升力系数自功率谱 Figure 4 Power spectral density of the lift at different spanwise positions with Q=0, 1 and 3 |
| ${p^*} = 10 \times {\rm{log}}\left( {\frac{{{p_{Q = i,{z^*} = j}}}}{{{p_{Q = 0,{z^*} = 1}}}}} \right),$ | (3) |
| ${f^*} = \frac{{f \cdot d}}{{{U_\infty }}}.$ | (4) |
式中:pQ=i, z*=j为Q=i, z*=j时功率谱峰值强度, pQ=0, z*=1为Q=0, z*=1时功率谱峰值强度, f为频率.
无论吸气与否, 模型所有高度上的无量纲涡脱频率都为0.116, 这表明顶部吸气虽然对脉动升力等有明显削弱作用, 但其不会改变模型涡脱落频率.Q=0时, 模型所有高度上的升力系数谱都具有明显峰值, 说明在不吸气时, 所有高度上展向涡都具有强烈的周期性.此外, 由于模型顶部所形成的下扫流具有削弱展向涡的特性, 因此, 越接近模型顶部功率谱峰值越弱.当Q=1时, 所有高度上功率谱峰值相对于Q=0时都明显减弱了, 且越接近顶部削弱得越显著.而当Q=3时, 功率谱峰值又有所增强.
综合图 3、4结果可知, 顶部吸气对模型所有高度上的展向涡脱具有抑制作用, 并可明显削弱C′d和C′l, 且距离顶部越近, 该控制效果越显著. Q=1时, 控制效果最为明显, 而当Q进一步增大至3时, 控制效果反而有所减弱.文献[17]也观察到了吸气控制效果并不随吸气速率增大而增强的现象.
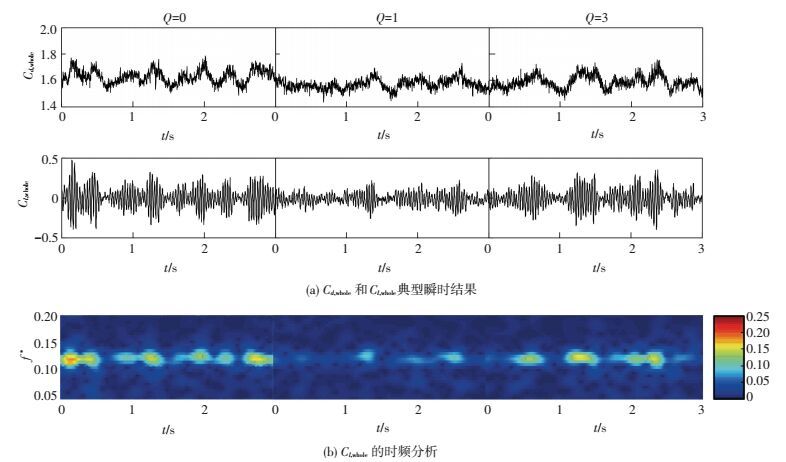
为进一步揭示顶部吸气对模型气动力的影响机理, 图 5给出了模型总体Cd, whole和Cl, whole的时程曲线以及Cl, whole对应的时频分析结果.由图 5可得到:首先, Q=0时, Cl, whole大幅波动的情形在时间上具有明显的间歇性, 时频谱中峰值是不连续的.这与文献[18-20]所观察到的现象一致, 即有限长方柱尾流中会随机出现两种典型状态:一种是方柱两侧展向涡有规律地交替脱落, 此时Cl, whole大幅振动;另一种是展向涡准对称地脱落, 对应Cl, whole振幅很小且无明显周期性.显然, 前者所对应的升力脉动值要显著大于后者.其次, Q=1时, Cd, whole和Cl, whole时程曲线表现得较为平稳, 这说明类似卡门涡街的交替涡脱模态在很大程度上被抑制了.而当Q=3时, Cl, whole的周期性波动再次变强.
|
图 5 模型总体气动力特性 Figure 5 Characteristics of the overall aerodynamic forces of the tested model |
为进一步探讨顶部剪切流的特性, 进行了流动显示实验.烟线布置见图 1(a), 发烟材料为石蜡.实验风速为1.12 m/s, 并以此调节吸气速度, 研究Q=0、1和3工况下方柱顶部流动特性.由于方柱没有雷诺数效应, 故该风速下的实验结果仍能为测压实验现象的解释提供参考. 图 6给出了Q=0、1和3时, 模型顶部剪切流的可视化结果.由图 6可以看出, Q=0时, 剪切流在模型顶部边缘发生分离, 分离流直接掠过模型顶部, 在其下游形成下扫流, 并与模型两侧形成的展向涡发生作用.这一下扫流具有将展向涡向两侧分开的趋势并能削弱展向涡的强度, 降低其脱落频率(相对于二维柱体)[21-22].当顶部前边缘吸气系数Q=1时, 顶部分离流被明显抑制并向模型顶部靠近.在狭缝吸气的作用下, 分离流在顶部的下游部分发生了再附着.随着向下游的发展, 流动再次在模型顶部后边缘发生分离, 并伴随有较为显著的不稳定性.从流动可视化图中可以看出, 该剪切流与模型展向涡在模型后部发生了较为强烈的相互作用, 这可能是此时脉动升力达到最小的原因.当Q增大到3时, 模型前边缘剪切流出现了另一种完全不同的形态.此时, 顶部前边缘的流动分离被完全抑制, 流动紧贴顶部表面向下游运动, 在顶面尾部发生分离, 且剪切流没出现如Q=1时的不稳定摆动.

|
图 6 Q=0、1和3时方柱顶部流动显示 Figure 6 Flow visualization near the cylinder free end with Q=0, 1 and 3 |
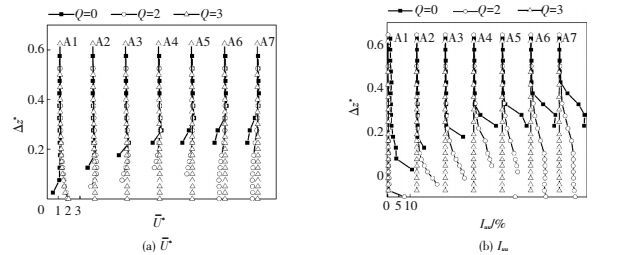
为了更进一步了解顶部剪切流在狭缝吸气作用下的变化情况, 用眼镜蛇探针在模型顶部A1~A7等不同位置处对剪切流进行了测量, 测点位置及探针布置如图 1所示.所用眼镜蛇探针为澳大利亚Turbulence Flow Instrumentation公司Cobra probe风速探针, 实验采样频率2 000 Hz, 采样时间约为15 s, 测量结果见图 7.其纵坐标Δz*为测点距模型顶部表面的距离. A1号位置为模型顶面前边缘, 在吸气狭缝的上游. 图 7(a)为上述测点位置上的流向时均速度U*, Q=0时, A1号位置处壁面附近速度明显减小;而Q=1和3时, 1号位置壁面附近测点速度不但没有减小, 反而都出现了明显加速.也就是说, 顶部前边缘的狭缝吸气对其上游气流有加速作用, 类似于对顶部剪切流注入了切向动量, 从而削弱或抑制顶部流动分离. A2号位置处, 壁面附近测点在Q=0时已无法获得有效测量数据, 表明这些测点都已处于流动分离区内.随着向下游发展, Q=0时剪切流在边缘分离后高度逐渐增大, 并将完全掠过顶面而不发生再附着.当Q=1时, 剪切流的高度被明显减小了, 并在A6位置附近在顶面发生了再附着.而当Q=3时, 分离流已被完全抑制, 不同位置测点均表现为相同的均匀分布.
|
图 7 方柱顶部剪切流测量结果 Figure 7 Distribution of U* and Iuu in the free-end shear layer |
图 7(b)给出了上述测点位置上的流向脉动速度Iuu. Q=0时, 顶部边缘形成的分离流的剪切层内Iuu最强, 但其距离顶面较远.前缘吸气在Q=1时不仅显著缩小了分离区, 而且仍保持了顶面附近较强的Iuu.而当Q增大到3时, 分离流被完全抑制后, 来自柱体前部的自由流紧贴着顶面流过, 此时顶面附近Iuu与自由流相同, 其强度几乎为零.由顶面剪切流的流动可视化与测量结果可知, Q=0时, 顶面前缘分离流直接掠过模型顶部, 并会在顶面上形成分离泡.而当Q=1时, 顶面上的分离流会发生再附着并明显抑制分离泡, 且此时顶面流动具有较高的湍流度, 这有利于模型尾流与外部高速流体进行动量交换, 并削弱展向漩涡脱落.而当Q增大到3时, 尽管顶部分离流被完全抑制, 但顶面流动湍流度几乎为零, 这可能反而削弱了尾流与外部高速流体的动量交换, 所以控制效果反而较Q=1时有所减弱.
3 结论采用风洞试验, 研究了H/d=5的正方形截面高层建筑简化模型顶部狭缝吸气对其气动力与顶部剪切流的控制效果, 得到如下结论:
1) 顶部狭缝吸气能够略微减小模型时均阻力, 并显著抑制模型脉动阻力与脉动升力.就本文吸气设置情况而言, 当吸气系数Q=1时, 气动力控制效果最为显著, 相对未控制工况, 时均阻力减小3.60%, 脉动阻力与脉动升力分别减小17.85%和45.57%.
2) 顶部狭缝吸气不仅对顶部附近气动力有影响, 而且对模型所有高度上的气动力均有显著控制效果.顶部吸气可削弱模型展向旋涡脱落, 但并未改变其涡脱落频率.
3) 狭缝吸气对模型顶部分离流有显著的加速作用, 并显著改变了分离流特性. Q=1时, 模型顶部流动分离被明显削弱, 并在顶面后部发生再附着;而当Q=3时, 流动分离被完全抑制, 且顶面上的边界层也基本消失.参考文献
| [1] |
TAMURA Y, KAREEM A.
Advancedstructural wind engineering[M]. Springer Japan, 2013: 377-383.
|
| [2] |
KIM Y C, BANDI E K, YOSHIDA A, et al. Response characteristics of super-tall buildings-Effects of number of sides and helical angle[J].
Journal of Wind Engineering and Industrial Aerodynamics, 2015, 145: 252-262.
DOI: 10.1016/j.jweia.2015.07.001 |
| [3] |
TANAKA H, TAMURA Y, OHTAKE K, et al. Experimental investigation of aerodynamic forces and wind pressures acting on tall buildings with various unconventional configurations[J].
Journal of Wind Engineering and Industrial Aerodynamics, 2012, 107/108: 179-191.
DOI: 10.1016/j.jweia.2012.04.014 |
| [4] |
KAREEM A, KIJEWSKI T, TAMURA Y. Mitigation of motions of tall buildings with specific examples of recent applications[J].
Wind & Structures And International Journal, 1999, 2(3): 201-251.
|
| [5] |
KWOK K C S, BAILEY P A. Aerodynamicdevices for tall buildings and structures[J].
Journal of Engineering Mechanics, 1987, 113(3): 349-365.
DOI: 10.1061/(ASCE)0733-9399(1987)113:3(349) |
| [6] |
DUTTON R, ISYUMOV N. Reduction of tall building motion by aerodynamic treatments[J].
Journal of Wind Engineering and Industrial Aerodynamics, 1990, 36(1-3): 739-744.
DOI: 10.1016/0167-6105(90)90071-J |
| [7] |
GU Ming, QUAN Yong. Across-wind loads of typical tall buildings[J].
Journal of Wind Engineering and Industrial Aerodynamics, 2004, 92(13): 1147-1165.
DOI: 10.1016/j.jweia.2004.06.004 |
| [8] |
ZHANG Hongfu, XIN Dabo, OU Jinping. Steady suction for controlling across-wind loading of high-rise buildings[J].
The Structural Design of Tall and Special Buildings, 2016, 25(15): 785-800.
DOI: 10.1002/tal.1283 |
| [9] |
ZHENG Chaorong, ZHANG Yaochun. Numerical investigation on the drag reduction properties of a suction controlled high-rise building[J].
Journal of Zhejiang University-Science A, 2010, 11(7): 477-487.
DOI: 10.1631/jzus.A0900593 |
| [10] |
郑朝荣. 高层建筑风荷载吸/吹气控制的数值模拟研究[D]. 哈尔滨: 哈尔滨工业大学, 2010.
ZHENG Chaorong. Numerical investigation of wind loads on high-rise buildings controlled by suction/blowing[D]. Harbin: Harbin Institute of Technology, 2010. |
| [11] |
郑朝荣, 张耀春. 分段吸气高层建筑减阻性能的数值研究[J].
力学学报, 2011, 43(2): 372-380.
ZHENG Chaorong, ZHANG Yaohchun. Numerical investigation of drag-reducing property for a high-rise building under subsection suction[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(2): 372-380. DOI: 10.6052/0459-1879-2011-2-lxxb2009-577 |
| [12] |
张继同. 主动吸气与被动气动控制下超高层建筑风荷载特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2015.
ZHANG Jitong. Characteristics of wind loads on super high-rise buildings under active suction control and passive aerodynamic control[D].Harbin: Harbin Institute of Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10213-1015981860.htm |
| [13] |
郑朝荣, 张继同, 张智栋. 凹角与吸气控制下高层建筑平均风荷载特性试验研究[J].
建筑结构学报, 2016(10): 125-131.
ZHENG Chaorong, ZHANG Jitong, ZHANG Zhidong. Experimental investigation on characteristics of mean wind loads of high-rise buildings controlled by corner recession and air-suction[J]. Journal of Building Structures, 2016(10): 125-131. |
| [14] |
WANG Hanfeng, ZHOU Yu. The finite-length square cylinder near wake[J].
Journal of Fluid Mechanics, 2009, 638: 453-490.
DOI: 10.1017/S0022112009990693 |
| [15] |
WANG Hanfeng, ZHOU Yu, CHAN C K, et al. Effect of initial conditions on interaction between a boundary layer and a wall-mounted finite-length-cylinder wake[J].
Physics of Fluids, 2006, 18(6): 065106.
DOI: 10.1063/1.2212329 |
| [16] |
UFFINGER T, ALI I, BECKER S. Experimental and numerical investigations of the flow around three different wall-mounted cylinder geometries of finite length[J].
Journal of Wind Engineering and Industrial Aerodynamics, 2013, 119: 13-27.
DOI: 10.1016/j.jweia.2013.05.006 |
| [17] |
CHEN Wenli, LI Hui, HU Hui. An experimental study on a suction flow control method to reduce the unsteadiness of the wind loads acting on a circular cylinder[J].
Experiments in Fluids, 2014, 55: 1707.
DOI: 10.1007/s00348-014-1707-7 |
| [18] |
SATTARI P, BOURGEOIS J A, MARTINUZZI R J. On the vortex dynamics in the wake of a finite surface-mounted square cylinder[J].
Experiments in Fluids, 2012, 52(5): 1149-1167.
DOI: 10.1007/s00348-011-1244-6 |
| [19] |
王汉封, 徐萌霞. 有限长正方形棱柱绕流的双稳态现象[J].
力学与实践, 2013, 35(3): 46-50.
WANG Hanfeng, XU Mengxia. Bistable phenomenon of the flow around a finite-length square prism[J]. Mechanics in Engineering, 2013, 35(3): 46-50. DOI: 10.6052/1000-0879-13-100 |
| [20] |
王汉封, 赵东伟, 邹超, 等. 高宽比为5的悬臂正方形棱柱气动力特性[J].
实验流体力学, 2015, 29(6): 8-15.
WANG Hanfeng, ZHAO Dongwei, ZOU Chao, et al. Aerodynamic forces of a cantilevered square prism with aspect ratio of 5[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(6): 8-15. |
| [21] |
SAKAMOTO H, ARIE M. Vortex shedding from a rectangular prism and a circular cylinder placed vertically in a turbulent boundary layer[J].
Journal of Fluid Mechanics, 1983, 126(126): 147-165.
|
| [22] |
PARK C, LEE S. Free end effects on the near wake flow structure behind a finite circular cylinder[J].
Journal of Wind Engineering and Industrial Aerodynamics, 2000, 88(2): 231-246.
DOI: 10.1016/S0167-6105(00)00051-9 |
 2017, Vol. 49
2017, Vol. 49


