约80%的混凝土结构裂缝是由于温度、湿度变化或自身因素作用下产生的非荷载应力造成的[1].混凝土早龄期变形为温湿变形,且混凝土温度场和湿度场的变化具有明显的非线性特征.Bazant等[2]对混凝土早龄期温度、湿度非线性特性进行了详细试验和理论研究,提出了考虑水分扩散和水泥水化耗水的混凝土内部湿度控制方程.混凝土的温升、自干燥及干燥作用往往同时存在,且各因素之间相互联系、相互影响,存在一种复杂的耦合作用[3].
混凝土构件内部湿度变化与其变形具有一定的相关关系.侯东伟[4]基于Kelvin方程,建立了考虑水化耗水和蒸发的收缩变形一体化计算模型,该模型考虑硅灰对混凝土早龄期饱和度的影响,但未考虑温湿度的相互影响.在没有外荷载影响的情况下,混凝土构件的应力来自周边构件或结构对变形的约束.康明[5]推导了混凝土配筋构件在周边约束下内部应力的量化计算模型.
本文基于水化度理论,考虑高强混凝土早龄期温湿度的相互影响,建立了高强混凝土早龄期温湿耦合模型,实现了高强混凝土棱柱体构件早龄期应变和温湿度场的模拟计算,并与既有的试验值进行对比.利用改进的计算模型对约束应力、温湿耦合效应及开裂风险进行计算分析.
1 温湿耦合模型 1.1 温度控制方程大量试验研究结果表明,当相对湿度降到一个特定数值时(75%左右),水化过程会减缓或者停止[6],因此,引入系数β(H)=[1+(5-5H)4]-1来考虑相对湿度对水化作用的影响,建立温度控制方程:
| $ \rho c\frac{{\partial T}}{{\partial t}} = \nabla \cdot \left( {kT} \right) + \beta \left( H \right)Q\left( T \right). $ | (1) |
式中:ρ为混凝土密度,取值为2 370 kg/m3;c为混凝土比热系数,取值17 J/(mm·h·℃);T为摄氏温度;k为混凝土传热系数,取值948.3 J/(kg·℃);Q(T)为混凝土水化放热项.
基于水化度理论[7]求解水化放热速率为
| $ \int_0^t {Q\left( T \right){\rm{d}}t} = {Q_{\rm{u}}}{M_{\rm{c}}}\frac{\alpha }{{{\alpha _{\rm{u}}}}}. $ | (2) |
式中:Qu为胶凝材料最终水化放热,取值为15 596 J/kg;α为混凝土水化度;Mc为胶凝材料用量,取值为650 kg/m3;
水化度的计算方法为[8]
| $ \alpha = {\alpha _{\rm{u}}}\exp \left[ { - {{\left( {\frac{A}{{{t_{\rm{e}}}}}} \right)}^B}} \right]. $ | (3) |
式中:te为混凝土的等效龄期, A和B为经验常数.
等效龄期由下式确定[8]:
| $ {t_{\rm{e}}} = \int_0^t {\exp \left( {1/R\left( {\frac{{{U_{{\rm{ar}}}}}}{{293}} - \frac{{{U_{{\rm{aT}}}}}}{{273 + T}}} \right)} \right){\rm{d}}t} . $ | (4) |
式中:R为理想气体常数, Uar为参考温度下的反应活化能, UaT为温度T下的反应活化能.
Uar、UaT由下式确定[9]:
| $ {U_{{\rm{ar}}}} = 41970\exp \left( { - 0.0034t} \right), $ | (5) |
| $ {U_{{\rm{aT}}}} = \left( {42830 - 43T} \right)\exp \left( {\left( { - 0.00017T} \right)t} \right). $ | (6) |
综上,混凝土水化热放热速率计算公式为
| $ Q\left( T \right) = \frac{{{Q_{\rm{u}}}}}{{{\alpha _{\rm{u}}}}}{M_{\rm{c}}}\alpha \frac{{AB}}{{t_{\rm{e}}^2}}{\left( {\frac{A}{{{t_{\rm{e}}}}}} \right)^{B - 1}}\exp \left[ {\frac{1}{R}\left( {\frac{{{U_{{\rm{ar}}}}}}{{293}} - \frac{{{U_{{\rm{aT}}}}}}{{273 + T}}} \right)} \right]. $ |
混凝土早龄期湿度控制方程为[2]
| $ \frac{{\partial H}}{{\partial t}} = \nabla \cdot \left[ {D\left( H \right){\rm{grad}}{H_{\rm{d}}}} \right] + \frac{{\partial {H_{\rm{s}}}}}{{\partial t}}. $ | (7) |
式中:H为相对湿度, D(H)为水分传输系数, Hd为混凝土蒸发扩散项, Hs为水化耗水项.
欧洲混凝土规范给出的传输系数D(H)的计算方法为
| $ D\left( H \right) = {D_{\max }}\left( {\beta + \frac{{1 - \beta }}{{1 + {{\left( {\frac{{1 - H}}{{1 - {H_c}}}} \right)}^\theta }}}} \right). $ | (8) |
式中:Dmax为饱和状态下的湿度扩散系数, Hc为湿度下降临界值, β和θ为经验系数.
式(8)关于D(H)的使用条件通常为恒温状态.如果温度机制在扩散过程中占主导地位,那么温度效应遵从速率过程理论[2],基于这个假设可以给出温度对扩散的影响系数[10]:
| $ f\left( T \right) = {\left( {\frac{{293}}{{273 + T}}} \right)^2}\exp \left[ {\frac{{{E_{{\rm{ad}}}}}}{R}\left( {\frac{1}{{293}} - \frac{1}{{273 + T}}} \right)} \right]. $ | (9) |
式中Ead为表观活化能.
从而可以得到受温度影响的混凝土扩散系数:
| $ D\left( {T,H} \right) = f\left( T \right)D\left( H \right). $ | (10) |
Oh等[11]提出了考虑水化度非线性变化的自干燥水化耗水计算模型:
| $ {H_{\rm{s}}} = \left( {{H_{{\rm{s,u}}}} - 1} \right){\left( {\frac{\alpha }{{{\alpha _{\rm{u}}}}}} \right)^\varphi }. $ | (11) |
式中:Hs, u为最终水化度对应的水化反应引起的相对湿度变化, φ为经验系数.
ZHANG等[9]以湿度饱和为临界点,对上述水化耗水计算模型进行了修正:
| $ {H_{\rm{s}}} = \left\{ {\begin{array}{*{20}{c}} {0,}&{\alpha \le {\alpha _{\rm{c}}};}\\ {\left( {1 - {H_{{\rm{s,u}}}}} \right){{\left( {\frac{{\alpha - {\alpha _{\rm{c}}}}}{{{\alpha _{\rm{u}}} - {\alpha _{\rm{c}}}}}} \right)}^\varphi },}&{\alpha > {\alpha _{\rm{c}}}.} \end{array}} \right. $ | (12) |
式中αc为湿度饱和期结束时的水化度.
湿度场计算所需各参数的取值见表 1.
| 表 1 湿度场计算参数取值 Table 1 Calculation parameter value of humidity field |
采用二维有限差分法,根据不同湿度分布和边界条件可分解为内部、绝湿和非绝湿3种节点情况.
对于内部节点,可将式(1)进行Grank-Nicholson变换得到二阶差分方程并变换为迭代形式:
| $ \begin{array}{*{20}{c}} { - {r_y}H_{i - 1,j}^{k + 1} + \left( {1 + 2{r_y}} \right)H_{i,j}^{k + 1} - {r_y}H_{i + 1,j}^{k + 1} = }\\ {{r_x}H_{i,j - 1}^k + \left( {1 - 2{r_x}} \right)H_{i,j}^k + {r_x}H_{i,j + 1}^k,} \end{array} $ | (13) |
| $ \begin{array}{*{20}{c}} { - {r_x}H_{i,j - 1}^{k + 2} + \left( {1 + 2{r_x}} \right)H_{i,j}^{k + 2} - {r_x}H_{i,j + 1}^{k + 2} = }\\ {{r_y}H_{i - 1,j}^{k + 1} + \left( {1 - 2{r_y}} \right)H_{i,j}^{k + 1} + {r_y}H_{i + 1,j}^{k + 1}.} \end{array} $ | (14) |
式中:i、j和k分别对应x、y轴节点编号及时间节点;
对于非绝湿节点可建立二阶差分格式并变为迭代形式:
| $ H_{i,j}^{k + 1} = {r_x}\left( {H_{i + 1,j}^k - H_{i,j}^k} \right) + H_{i,j}^k. $ | (15) |
对于非绝温节点可建立一阶差分格式并变为迭代形式:
| $ H_{i,j}^t = {H_a} + \frac{{D\left( H \right)}}{{{a_{\rm{m}}}\Delta x}}\left( {H_{i + 1,j}^t - H_{i,j}^t} \right). $ | (16) |
式中:Ha为与外表面接触的环境相对湿度, am为混凝土表面水分扩散系数.
Yuan等[12]给出了表面节点水分传输系数的计算方法:
| $ {a_{\rm{m}}} = A\left( {0.253 + 0.06{v_{\rm{a}}}} \right)\left( {H - {H_{\rm{a}}}} \right). $ | (17) |
式中:A为经验系数, va为混凝土表面风速, Ha为外界环境相对湿度.温度场的模拟与湿度场类似,不再具体说明.
1.4 湿度应变计算模型侯东伟[4]根据Kelvin方程,在大量试验和理论研究的基础上[4, 13-15],建立了以相对湿度为主要变量的考虑水化耗水和蒸发的收缩变形一体化计算模型:
| $ {\varepsilon _{{\rm{sh}}}} = \left\{ \begin{array}{l} \eta \left[ {1 - \sqrt[3]{{1 - \left( {{V_{{\rm{cs}}}} - {V_0}} \right)}}} \right],\;\;\;\;\;\;\;H = 100;\\ \eta \left[ {1 - \sqrt[3]{{1 - \left( {{V_{{\rm{cs}}}} - {V_0}} \right)}}} \right] - \\ \frac{{S{\rho _{\rm{w}}}R\left( {T + 273} \right)}}{{3M}}\left( {\frac{1}{K} - \frac{1}{{{K_s}}}} \right)\ln H,H \le 100. \end{array} \right. $ | (18) |
式中:η为化学减缩修正系数;M是水的摩尔质量;ρw是水的密度;Ks是不含孔介质体积弹性模量;
成熟混凝土只需要考虑混凝土饱和度与相对湿度之间的关系,因为其微观孔结构相对稳定,但是早期混凝土中水化作用导致微孔结构不断演变,直接影响到其热湿传输过程[17].
DU等[18]建立了混凝土水化度、温度、湿度与饱和度的关系:
| $ S\left( {\alpha ,T,H} \right) = 1 - \exp \left[ {m{{\rm{e}}^{n\alpha }} \cdot \frac{{2\gamma M}}{{\rho RT\ln H}}} \right]. $ | (19) |
式中:m、n为材料参数, γ为液体表面张力系数.
弹性模量是混凝土早龄期应力应变的重要影响参数,本文采用基于水化度理论弹性模量的计算方法[19]:
| $ E\left( \alpha \right) = 1.05{E_{28}}{\left( {\frac{{\alpha - {\alpha _{\rm{0}}}}}{{{\alpha _{\rm{u}}} - {\alpha _{\rm{0}}}}}} \right)^b}. $ | (20) |
式中:E28为28 d弹性模量, α0为水泥凝结时的水化度, b为经验系数.
湿度变形计算所需各参数的取值见表 2.
| 表 2 湿度变形计算参数取值 Table 2 Calculation parameter value of moisture transformation |
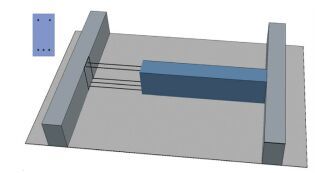
混凝土构件早龄期变形会受到内部钢筋和骨料以及周边相邻构件的约束而产生约束应力,当约束应力超过混凝土抗拉强度则会导致构件开裂.图 1为工程中常见的一种受约束混凝土构件形式.
|
图 1 计算模型横截面 Figure 1 Cross section of model |
以此构件为例,可建立计算模型.基本假设为:1)混凝土为各向同性材料;2)湿度分布沿梁的长度方向不变;3)接触不发生湿度交换;4)钢筋和混凝土之间没有相对滑移;5)构件底部不受摩擦力等约束限制.根据混凝土构件受到的约束特点,建立图 2的计算模型.

|
图 2 约束应力计算模型 Figure 2 Calculation of restrained deformation |
康明[5]将端部约束看成弹簧系统,根据位移平衡条件和力平衡条件得到混凝土的应力增量:
| $ {\sigma _{\rm{c}}} = {E_{\rm{c}}}\frac{{{\varepsilon _{{\rm{sh}}}}\left( {\frac{{{E_{\rm{R}}}}}{{{E_{\rm{c}}}}} + \frac{{{E_{\rm{s}}}{A_{\rm{s}}}}}{{{E_{\rm{c}}}{A_{\rm{c}}}}}} \right) - {a_{\rm{c}}}\Delta T\left( {\frac{{{E_{\rm{R}}}}}{{{E_{\rm{c}}}}} + \frac{{{E_{\rm{s}}}{A_{\rm{s}}}}}{{{E_{\rm{c}}}{A_{\rm{c}}}}}} \right) + {a_{\rm{s}}}\Delta T\frac{{{E_{\rm{s}}}{A_{\rm{s}}}}}{{{E_{\rm{c}}}{A_{\rm{c}}}}}}}{{\frac{{{E_{\rm{R}}}}}{{{E_{\rm{c}}}}} + \frac{{{E_{\rm{s}}}{A_{\rm{s}}}}}{{{E_{\rm{c}}}{A_{\rm{c}}}}} + 1}}. $ | (21) |
式中:εsh为混凝土自由收缩应变;Ec和Es分别为混凝土和钢筋的弹性模量;Ac和As分别为混凝土和钢筋的计算截面积;
根据应力松弛系数法计算受徐变影响的约束应力,并将时间离散,分别计算等长时间段内的应力增量,然后叠加,可得某时刻的应力值:
| $ \begin{array}{*{20}{c}} {\sigma \left( {{t_{i + 1}}} \right) = \sigma \left( {{t_0}} \right)\left[ {1 - \frac{{\varphi \left( {{t_0}} \right)}}{{1 + \chi \left( {{t_0}} \right)\varphi \left( {{t_0}} \right)}}} \right] + }\\ {\sum\limits_{i = 1}^n {\sigma \left( {{t_{i + 1}},{t_i}} \right)\left[ {1 - \frac{{\varphi \left( {{t_{i + 1}},{t_i}} \right)}}{{1 + \chi \left( {{t_{i + 1}},{t_i}} \right)\varphi \left( {{t_{i + 1}},{t_i}} \right)}}} \right]} .} \end{array} $ |
式中:φ(ti+1, ti)=0.9ti-0.32(ti+1-ti)0.32为徐变系数[14];χ(ti+1,ti)为经验参数,取1.
2.3 开裂风险分析混凝土早龄期抗拉强度可以用水化度来推算[20]:
| $ f\left( \alpha \right) = \zeta {f_{28}}{\left( {\frac{{\alpha - {\alpha _{\rm{0}}}}}{{{\alpha _{\rm{u}}} - {\alpha _{\rm{0}}}}}} \right)^\tau }. $ | (22) |
式中:ζ为经验常数,取1.1;f28为混凝土28 d抗拉强度,取3.1 MPa;τ为经验常数,取0.5.
一般将混凝土在某时刻的实际拉应力与抗拉强度的比值σ(t)/f(α)作为开裂风险,但混凝土的力学性能具有明显的波动性,一般认为当开裂风险达到0.7时,混凝土开裂的可能性需要足够的重视[21].
3 计算结果与分析 3.1 模型验证文献[4]提供了水胶比为0.30,截面尺寸为60 mm×100 mm的混凝土轴向自由收缩构件28 d龄期内温度、相对湿度和应力的试验结果,以此作为对计算模型正确性的验证.其混凝土配比见表 3.
| 表 3 混凝土配合比 Table 3 Concrete mix ratio |
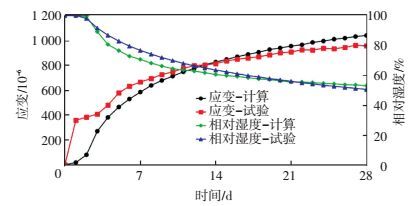
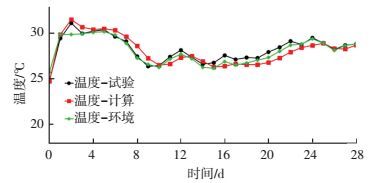
图 3、4为相对湿度、温度和应变的计算值与参考文献试验结果的对比.结果表明:相对湿度在3 d~14 d范围内模型计算值较试验值略大,主要因为模型计算过程未考虑试验中出现的泌水现象引起的水分分布不均匀;浇筑完成至4 d的应变计算值比试验值小,是因为模型仅考虑化学缩减和干缩这两类主要的变形来源,未考虑沉降变形和塑性变形等因素;随着相对湿度的降低,构件轴向应变逐渐增大,截面中心相对湿度在28 d达到50.45%,对应的应变值为1.04×10-3;由于水化放热的影响,温度在1 d~3 d龄期出现明显升高,之后与环境温度变化基本一致;采用本文的计算方法,可以较好地描述混凝土早龄期相对湿度、应变和温度的变化规律.
|
图 3 模型计算结果与文献试验结果的比较 Figure 3 Comparison between model and test |
|
图 4 计算温度与文献试验结果的比较 Figure 4 Temperature comparison between model and test |
JGJ/T 281—2012《高强混凝土应用技术规程》中规定,高强混凝土可采取潮湿养护,并可采取蓄水、浇水、喷淋洒水或覆盖保湿等方式,潮湿养护时间不宜少于10 d,因此,下文算例选择对截面尺寸60 mm×100 mm的C80高强混凝土构件28 d龄期内的温湿度耦合效应进行计算分析,浇水养护时间为10 d,然后置入温度20 ℃,相对湿度20%的环境中.
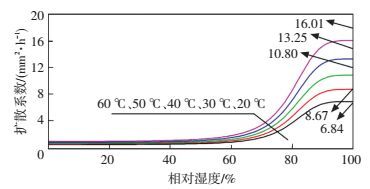
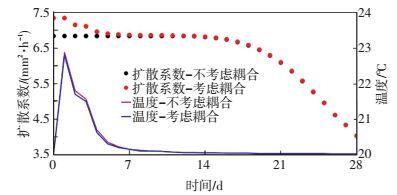
湿度扩散系数会受到湿度和温度的双重影响.由图 5可知,相对湿度大于60%时,扩散系数较大,此时混凝土内部的液态水含量较高,对扩散性的影响显著[10],相对湿度小于60%时,扩散系数基本保持不变;相对湿度大于60%时,随着温度的升高,扩散系数也明显增大,当相对湿度为100%时,60 ℃时的扩散系数为20 ℃时扩散系数的2.3倍.从图 6可以看出,混凝土温度在7 d龄期内有明显的升温和降温过程,最大升温不超过3 ℃,考虑耦合作用的混凝土扩散系数在7 d龄期内出现明显变大,但由于养护时间为10 d,因此对湿度扩散和混凝土变形的影响较小;7 d至28 d龄期,耦合效应对扩散系数影响极小.
|
图 5 扩散系数随相对湿度的发展 Figure 5 The diffusion coefficient varying with relative humidity |
|
图 6 扩散系数和温度随时间的发展 Figure 6 Diffusion coefficient and temperature over time |
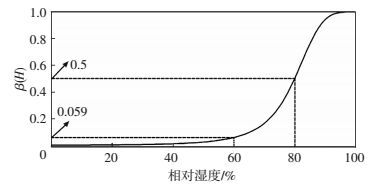
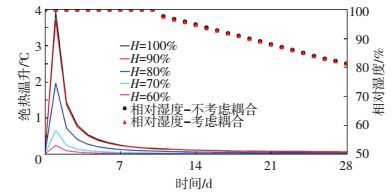
由图 7可知,相对湿度为100%时,水化热影响系数β(H)为1,当相对湿度为80%时,β(H)为0.5,若相对湿度降为60%,则β(H)为0.059,因此,相对湿度对水化热的影响明显,这一点也可由图 8看出,湿度为100%的最大绝热温升为60%时的16.9倍,80%时的2倍,相关文献研究指出,当相对湿度降低到约75%时,水化反应会大大减缓或者停滞[22].由图 8还可知,耦合效应对相对湿度的影响极小,由于混凝土温度变化明显的7 d龄期内是处于浇水养护条件下,对混凝土早龄期的湿度影响极小,可忽略不计.
|
图 7 水化热影响系数随相对湿度的发展 Figure 7 Effect of hydration heat coefficient with the development of relative humidity |
|
图 8 相对湿度和绝热温升随时间的发展 Figure 8 Relative humidity and adiabatic temperature rise over time |
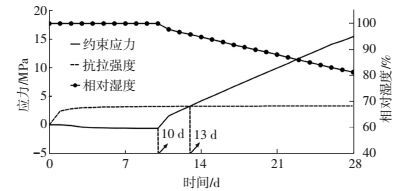
计算了环境温度20 ℃,环境湿度20%的环境条件下,配筋率为1.5%,截面尺寸为60 mm×100 mm,约束度为1的C80高强混凝土的28 d龄期内应力变化规律和开裂风险,见图 9、10.
|
图 9 应力与相对湿度 Figure 9 Stress and relative humidity |
|
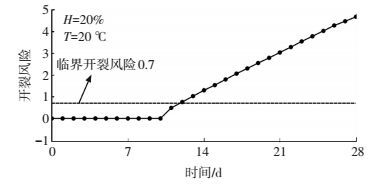
图 10 开裂风险 Figure 10 Cracking risk |
由图 9可知,相对湿度在10 d龄期内基本为100%,养护结束后开始下降,28 d龄期降至81.3%;应力在10 d龄期内基本为0 MPa,10 d龄期后开始上升,在13 d龄期达到混凝土抗拉强度,28 d达到15.4 MPa.11 d龄期的开裂风险达到0.7,实际工程中有可能在28 d之前出现开裂,使应力得到释放,所以应力不会达到15.4 MPa.由图 10可知,10 d龄期内的开裂风险基本为0,12 d龄期的开裂风险达到0.7,12 d至28 d龄期开裂风险呈线性增长.
4 结论1) 建立的温湿耦合变形计算模型能够较好预测高强混凝土温度、相对湿度和应变的变化.
2) 相对湿度较高时,温度对扩散系数的影响较明显,对应的水化热影响系数变化幅度大.
3) 在浇水养护条件下,小体积混凝土的温湿耦合作用不明显;由于水化升温较小,温度对约束应力的影响可以忽略;养护结束以后相对湿度对约束应力的影响明显,会使构件开裂风险变大.
| [1] |
朱伯芳.
大体积混凝土温度应力与温度控制[M]. 北京: 中国电力出版社, 1999.
ZHU Bofang. Thermal stresses and temperature control of mass concrete[M]. Beijing: China Electric Power Press, 1999. |
| [2] |
BAZANT Z P, NAJJAR L J. Nonlinear water diffusion in nonsaturated concrete[J].
Materials and Structures, 1972, 5(1): 3-20.
|
| [3] |
杜明月. 基于微孔结构演化的早龄期混凝土热-湿-力耦合模型研究[D]. 浙江: 浙江大学, 2015.
DU Mingyue. Thermo-hygro-mechanical model of early-age concrete based on micro-pore structure evolution[D]. Zhejiang: Zhejiang University, 2015. |
| [4] |
侯东伟. 混凝土自身与干燥收缩一体化及相关问题研究[D]. 北京: 清华大学, 2010.
HOU Dongwei. Integrative studies on autogenous and drying shrinkage of concrete and related issues[D]. Beijing: Tsinghua University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10003-1012006556.htm |
| [5] |
康明. 施工期钢筋混凝土构件的约束收缩变形性能研究[D]. 重庆: 重庆大学, 2010.
KANG Ming.A thesis submitted to chongqing university in partial fulfillment of the requirement for the degree of doctor of engineering[D]. Chongqing: Chongqing University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10611-2010215554.htm |
| [6] |
GAWIN D, PESAVENTO F, SCHREFLER B A. Hygro-thermo-chemo-mechanical modelling of concrete at early ages and beyond, Part Ⅰ: hydration and hygro-thermal phenomena[J].
International Journal for Numerical Methods in Engineering, 2006, 67: 299-331.
DOI: 10.1002/(ISSN)1097-0207 |
| [7] |
SCHINDLER A K, FOLLIARD K J. Heat of hydration models for cementitious materials[J].
ACI Materials Journal, 2005, 102(1): 24-33.
|
| [8] |
PANE I, HANSENA W. Concrete hydration and mechanical properties under nonisothermal conditions[J].
ACI Materials Journal, 2002, 99(6): 534-422.
|
| [9] |
ZHANG J, QI K, HUANG Y. Calculation of moisture distribution in early age concrete[J].
ASCE Journal of Engineering Mechanics, 2009, 135(8): 871-880.
DOI: 10.1061/(ASCE)0733-9399(2009)135:8(871) |
| [10] |
杜明月, 田野, 金南国, 等. 基于水泥水化的早龄期混凝土温湿耦合[J].
浙江大学学报(工学版), 2015, 49(8): 1410-1416.
DU Mingyue, TIAN Ye, JIN Nanguo, et al. Coupling of hygro-thermal field in early-age concrete based on cement hydration[J]. Journal of Zhejiang University(Engineering Science), 2015, 49(8): 1410-1416. |
| [11] |
OH B H, CHA S W. Nonlinear analysis of temperature and moisture distributions in early-age concrete structures based on degree of hydration[J].
ACI Materials Journal, 2003, 100(5): 361-370.
|
| [12] |
YUAN Y, Wan Z L. Prediction of cracking within early-age concrete due to thermal, drying shrinkage and creep behavior[J].
Cement & Concrete Research, 2002, 32(7): 1053-1059.
|
| [13] |
张智博, 张君. 混凝土收缩与环境湿度的关系研究[J].
建筑材料学报, 2006, 9(6): 720-723.
ZHANG Zhibo, ZHANG Jun. Experimental study on relationship between shrinkage strain and environmental humidity of concrete[J]. Journal of Building Materials, 2006, 9(6): 720-723. |
| [14] |
BENTZ D P, GARBOCZI E J, QUENARD D A. Modeling drying shrinkage in reconstructed porous materials: application to porous Vycor glass[J].
Modeling And Simulation In Materials Science And Engineering, 1999, 6(3): 211-236.
|
| [15] |
ZHANG Jun, HOU Dongwei, HAN Yudong. Micromechanical modeling on autogenous and drying shrinkages of concrete[J].
Construction and Building Materials, 2012, 29(3): 230-240.
|
| [16] |
JENSEN O M.
Autogenous deformation and RH-change-self-desiccation and self-desiccation shrinkage[M]. Denmark: The Technical University of Denmark, 1993.
|
| [17] |
BARY B, RANC Q, DURAND S. A coupled thermo-hydro-mechanical-damage model for concrete subjected to moderate temperatures[J].
International Journal of Heat and Mass Transfer, 2008, 51(11/12): 2847-2862.
|
| [18] |
DU Mingyue, JIN Xianyu, YE Hailong, et al. A coupled hygro-thermal model of early-age concrete based on micro-pore structure evolution[J].
Construction and Building Materials, 2016, 111: 689-698.
DOI: 10.1016/j.conbuildmat.2015.10.187 |
| [19] |
SCHUTTER G D. Applicability of degree of hydration concept and maturity method for thermo-visco-elastic behaviour of early age concrete[J].
Cement & Concrete Composites, 2004, 26: 437-443.
|
| [20] |
GUTSCH A W. Properties of early age concrete-Experiments and modelling[J].
Materials and Structures, 2002, 35(2): 76-79.
DOI: 10.1007/BF02482104 |
| [21] |
SPRINGENSCHMIDR.
Prevention of thermal cracking in concrete at earlyages[M]. London: E & FN Spon, 1998: 60-62.
|
| [22] |
BAŽANT Z P, PRASANNAN S. Solidification theory for concrete creep. Ⅰ: Formulation.Ⅱ: Verification and application[J].
Journal of Engineering Mechanics, 1989, 115(8): 1691-1725.
DOI: 10.1061/(ASCE)0733-9399(1989)115:8(1691) |
 2017, Vol. 49
2017, Vol. 49


