2. 交通运输部公路科学研究院,北京 100088;
3. 中铁大桥勘测设计院集团有限公司,武汉 430050
2. Research Institute of Highway Ministry of Transport, Beijing 100088, China;
3. China Zhongtie Major Bridge Reconnaissance & Design Institute Co., Ltd., Wuhan 430050, China
斜拉桥是由塔、梁、索3种基本构件组成的结构,以塔主要受压,梁主要受轴向压力和横向弯矩,索受拉为主要特征,是一种具有良好发展前景的大跨度桥梁形式.与另一大跨度桥梁结构悬索桥相比,斜拉桥具有更大的刚度及更好的抗风性能,在实际工程中广泛应用[1-2].
近年来,由于计算分析水平和材料技术的不断提高,桥梁设计方法得到快速发展,索塔结构形式不断变化,出现了越来越多的新型构造[3],如西班牙无背索竖琴式独塔斜拉桥Alamillo Bridge[4]、天津摩天轮和新型斜拉桥复合结构慈海桥[5]、新加坡外侧偏置斜八边形变截面独柱斜拉桥Safti Link Bridge[6].新型结构体系的出现以及斜拉桥跨持续增加,使索塔锚固区构造十分复杂,受力增加,应力分布状态并不明确[7],因此,锚固区的传力机理是斜拉桥索塔锚固区设计的关键技术问题.
分组集聚式索塔锚固体系是近年来出现的一种创新型构造,目前仅应用于韩国巨加大桥[8]与本文介绍的某公路大桥.索塔锚固区是传递索力至塔柱的重要部位,由于分组集聚式索塔锚固区形状与构造不规则,锚固区集中索力较大,加上孔洞削弱,使锚固区应力分布复杂,钢箱梁与混凝土桥塔结合处受力不明确.因此,为保证桥梁结构的安全,需要对索塔锚固区进行深入细致的分析[9].
本文以某公路大桥为工程背景,运用ABAQUS软件建立索塔锚固区节段有限元模型,利用桥塔等效杆系模型分析结果确定节段模型的荷载及边界条件,计算分析了各工况下混凝土桥塔及钢横梁的应力分布.通过对钢-混界面的各向应力及位移分布研究,探讨在不同程度预应力损失和钢-混界面摩擦系数影响下钢横梁与混凝土桥塔的传剪受力机理,为分组集聚式索塔锚固形式斜拉桥设计和施工提供重要参考依据.
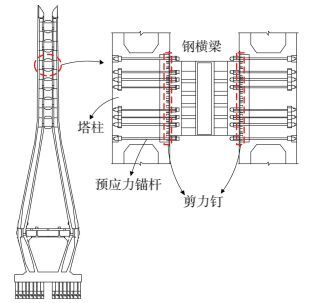
1 工程概况某公路大桥主桥采用双塔双索面混合梁斜拉桥结构,桥跨布置为3×48+96+828+280+100=1 448 m,主线采用双向6车道,桥塔形式采用钻石型设计.与一般斜拉桥拉索分散锚固方式不同,双肢薄壁混凝土塔柱之间通过6道钢横梁连接,每道钢横梁锚固6~10对斜拉索,斜拉索分别在6个钢横梁内部钢锚箱上采用分组集聚式锚固方式.钢横梁长7 m,高7 m,桥塔高237 m,每道钢横梁净距9 m,索塔断面见图 1,全桥立面见图 2.
|
图 1 某桥索塔断面图 Figure 1 Cross-section of the bridge cable-pylon |

|
图 2 某桥全桥立面图 Figure 2 Elevation drawing of the bridge |
由于斜拉索在单点集中锚固,导致分组集聚式索塔锚固区承受很大的集中荷载,为保证钢横梁与桥塔可靠连接,钢横梁-混凝土塔结合处采用2道防线:1)钢横梁端部与混凝土桥塔采用锚杆对拉锚固方式,使结合面产生较大法向压应力,利用钢横梁-混凝土塔之间的摩擦效应抵抗钢横梁传来的竖向剪力;2)混凝土与钢横梁界面焊有大量剪力钉,抵抗钢-混界面若摩擦力失效产生的相对滑移.
2 索塔锚固区数值模型 2.1 简化与假定由于锚固区构造十分复杂,为提高计算效率,在尽可能减小对结构影响的前提下进行了部分简化和假定,主要包括:
1) 由于塔柱两肢及钢横梁均沿钢横梁中心对称,索力与锚杆张拉力在中心两侧相同,因此忽略桥塔两肢塔柱内力不相同的影响,提取塔柱内力时考虑对称加载边界条件,边界条件数值按杆系模型实际计算结果提取.
2) 偏于安全考虑,未考虑预应力锚杆埋入混凝土部分作用,仅考虑锚杆与后锚板连接作用.
3) 混凝土塔柱内纵筋采用换算面积,按配筋率相等原则将4根简化为1根.
2.2 数值模型的建立全塔整体模型包括原结构整体塔柱及6道锚固区钢横梁,选取受力最不利的最下部钢横梁进行分析.由于钢横梁间净距9 m,最下部钢横梁以下20 m处塔柱壁厚减小,因此截取范围为钢横梁及其上4.5 m其下10 m范围内混凝土塔柱,采用有限元软件ABAQUS建立精细有限元模型.由于索塔锚固区混凝土与钢板空间关系复杂,塔柱与钢横梁难以划分为规则的六面体及四边形单元,为了便于单元网格的划分,混凝土塔柱有限元模型选择C3D4四面体实体单元,钢横梁采用四边形和三角形混合单元划分S4R壳单元,并通过适当减小单元尺寸来弥补单元形状带来的计算精度上的损失.预应力锚杆、钢筋及剪力钉选择B31梁单元,材料力学指标见表 1,Q370E的容许弯曲应力为210 MPa.
| 表 1 材料参数 Table 1 Parameters of materials |
钢横梁与混凝土塔柱通过预应力锚杆张拉紧密贴合,以摩擦力抵抗竖向索力.为真实模拟钢-混组合结构受力,模型中建立接触单元模拟混凝土塔柱与钢横梁承压板接触关系:法向采用硬接触,接触压力变为零前,接触面不分离;切向采用库伦摩擦接触,文献[10]根据试验分析,得到钢-混摩擦系数为0.57~0.69,规范[11]中规定支座端板钢-混摩擦系数为0.3,同时参考文献[12]中钢-混截面摩擦系数取值0.3,考虑摩擦系数受材料特征及接触面处理方法影响较大,为偏于安全,分析中摩擦系数取为0.3,切向力达到临界切应力前,接触面不发生相对滑动.
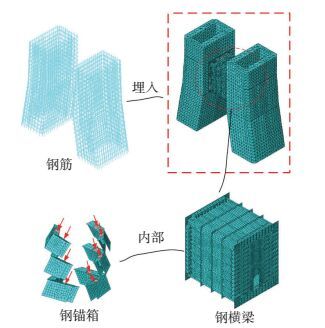
模型中钢筋全部嵌入混凝土塔柱,剪力钉一端与钢横梁连接,其余部分嵌入塔柱内部,计算时通过位移差值自动满足位移协调条件,索塔锚固区有限元模型见图 3.
|
图 3 索塔锚固区有限元模型 Figure 3 Finite element model of cable-pylon anchorage |
图 4为塔柱与钢横梁连接情况.为减小锚杆预应力施加过程中造成板件局部应力集中现象,锚杆与钢结构板件连接时均先与方形垫片连接,再使垫片与板件连接.

|
图 4 塔柱与钢横梁板件连接示意 Figure 4 Connection of concrete pylon and steel box girder |
塔柱与钢横梁间的连接主要通过锚杆施加预应力实现.锚杆分为两部分:一部分连接后锚板与钢横梁锚板,另一部分连接背板与承压板.其中后锚板嵌入塔柱内部,背板为空心塔柱内壁“狗骨形”板件,承压板与锚板为钢横梁外侧两层板件.
2.3 荷载条件与工况根据索塔实际受力情况,考虑荷载种类及施加方式:
1) 结构重力荷载:通过对整体模型施加重力加速度实现,3种工况下荷载分别为:2 468.2、6 142.1、10 411.0 kN.
2) 锚杆张拉力:所有锚杆张拉力均为150 t,以降温法形式实现.
3) 索力:采用对钢锚箱上索锚板施加压力实现,根据拉索角度计算索锚板压力,索力作用点位置见图 3.
为了研究索塔及钢横梁在各阶段受力状态,以下分析共分为3种工况,考察锚固区在不同荷载组合下的受力性能及1.7倍设计荷载下的安全储备.
工况1为施工完成时成桥受力状态;工况2为最不利设计荷载工况,其中索力及横梁竖向反力考虑恒载+活载+制动力+风荷载+温度荷载+沉降组合;工况3为1.7倍最不利设计荷载组合,考察极限状态下锚固区性能.各工况荷载均为重力+锚杆张拉力+索力+荷载条件及边界条件,其中各工况索力的施加根据表 2选取.
| 表 2 斜拉索索力 Table 2 Stayed cable forces |
为确定索塔节段模型荷载条件及边界条件,利用MIDAS软件建立如图 5所示的索塔结构等效杆系有限元模型,进行各个工况下索塔受力分析.为提高计算效率,在保证模型能够满足实际结构受力情况基础上,整体模型中仅建立受力较不利的北塔进行分析.在MIDAS杆系模型中,通过建立轴向刚度较小的短拉杆施加斜拉索索力,短拉杆空间倾角与斜拉索保持完全一致.

|
图 5 全塔杆系模型 Figure 5 Equivalent beam element model |
根据各工况下等效杆系模型计算结果,提取相应节段模型边界处内力作为精细模型荷载及边界条件.由于MIDAS杆系模型中塔柱两塔肢距离为净距,赋予塔肢截面属性时,以杆件处向两侧进行截面偏移(图 5).因此为与杆系模型一致,精细模型中荷载及边界条件施加于塔肢截面内侧中心处,见图 6.

|
图 6 节段模型荷载条件及边界条件 Figure 6 Loading and boundary conditions of sectional model |
| 表 3 节段模型荷载条件及边界条件 Table 3 Loading and boundary conditions of sectional model |
在钢横梁锚固体系中,塔柱与钢横梁紧密相连,混凝土承受钢横梁传来的全部竖向与部分水平索力,并且受到锚杆预压力作用,在钢-混连接处存在接触应力,使锚固区索塔应力分布非常复杂,因此,需要考察在各荷载工况下混凝土索塔的应力,以评价结构整体的安全性.
各工况塔柱最大正应力分析结果见表 4,各工况混凝土索塔最大压应力均小于C50混凝土抗压强度设计值23.1 MPa,混凝土最大拉应力均小于抗拉强度设计值1.89 MPa.在1.7倍的设计荷载下(工况3),混凝土最大拉应力仅为1.3 MPa,桥塔安全储备较高.
| 表 4 塔柱最大正应力计算结果 Table 4 Max normal stress of cable-pylon |
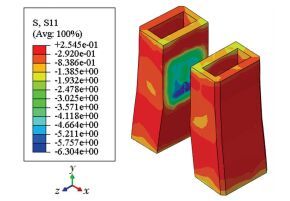
图 7为工况2荷载作用下塔柱S11应力云图,在最不利设计荷载作用下,混凝土与钢横梁承压板连接位置处始终处于受压状态,钢横梁与混凝土始终不分离.
|
图 7 索塔S11应力云图 Figure 7 S11 stress contour of cable-pylon under case 2 |
分组集聚体系斜拉桥中,拉索在钢横梁处集中锚固,使钢横梁承受巨大的集中荷载,钢横梁设计合理、传力明确成为设计中的重要环节.
为减小索力作用下钢锚箱产生应力集中,斜拉索首先作用于拉索垫板,索力经钢锚箱传至竖向与横向隔板,最后通过外侧承压板将竖向索力及部分水平力以摩擦力形式传给塔柱,其余大部分水平向力则由钢横梁承担.
整体桥塔中钢横梁承受了较大拉力,混凝土承受了较大压力和较少拉力,充分发挥了钢材抗拉强度高和混凝土承压强度大的优点,克服了钢材承压易失稳和混凝土受拉易开裂的缺点,是良好的传力系统.
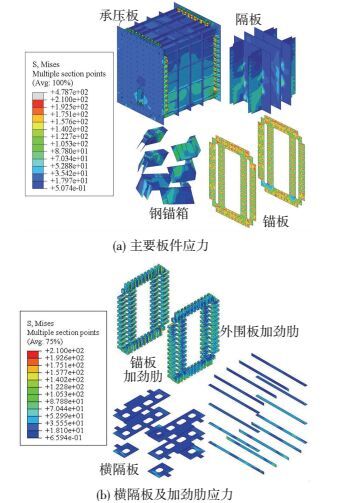
工况2作用下钢横梁各板件Von Mises应力云图见图 8,各工况荷载作用下钢横梁板件最大Von Mises应力计算结果见表 5.由于锚板上连接有大量预应力锚杆且锚垫板的面积较小,锚板开锚杆孔部分出现明显的应力集中现象,钢锚箱由于直接承受索力导致应力较大,此种状况均可通过增加垫板缓解.锚固区钢横梁其余板件应力水平均控制在容许弯曲应力210 MPa以下,钢横梁具有足够的安全储备.其中钢横梁隔板、承压板及横隔板最大应力不足容许应力1/2,可适当减小相应板厚以减少材料用量避免浪费,在确保桥梁安全性的前提下节省造价.
|
图 8 钢横梁板件应力云图 Figure 8 Von Mises stress contour of plates of steel box girder |
| 表 5 钢横梁最大Von Mises应力计算结果 Table 5 Max Von Mises stress of steel box girder |
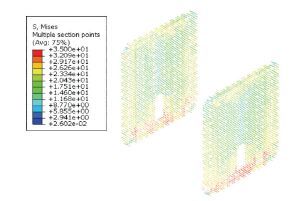
荷载作用下各工况剪力钉及锚杆应力计算结果见表 6.工况2荷载作用下剪力钉应力分布见图 9.可以看出,最不利设计荷载作用下剪力钉应力较小,远低于屈服应力.由于索力水平向分力相互抵消,剪力钉应力基本沿xy平面对称,由人洞上方向两边逐渐增大.在索力竖向分力影响下,剪力钉应力随高度的增加而减小,底部最大应力约为35 MPa.
| 表 6 连接件最大Von Mises应力结果 Table 6 Max Von Mises stress of connectors |
|
图 9 工况2剪力钉Von Mises应力云图 Figure 9 Von Mises stress contour of shear studs under case 2 |
最不利设计荷载工况2索力施加前后锚杆应力分布情况见图 10.锚杆应力呈现中间小两边大,与预应力施加结束时相比,所有索力施加结束时锚杆应力变化不大,约为395 MPa,远小于屈服强度835 MPa,锚杆具有足够的安全性.

|
图 10 索力施加前后,工况2锚杆Von Mises应力云图 Figure 10 Von Mises stress contour of bolt under case 2, before and after the cable force |
钢-混组合结构中,钢结构与混凝土界面上剪力的有效传递是结构整体工作的前提,为保证两者共同受力,通常需要设置剪力连接键.
目前,常用的有限元方法对于钢-混结合段的模拟有两种,即简化模型与精细模型.简化模型一般将剪力键的荷载-滑移特性视为线性或直接粘结处理,往往与实际结构受力特性不符[13].精细模型中多将剪力键以弹簧单元模拟,而弹簧单元模拟剪力钉存在以下2个问题:一方面,弹簧刚度由推出试验确定,剪力钉在试验中受力状况与实际受力情况存在差异;另一方面,弹簧单元只能提取剪力钉单向受力情况,而不能提取剪力钉的应力情况,因此,用弹簧单元拟剪力钉会由于刚度的取值不同而产生较大的误差,利用梁单元模拟剪力钉则能克服上述不足[14].
某公路大桥索塔由于采用锚杆对拉锚固方式,使结合面产生较大法向压应力,索力作用下,钢横梁传来巨大竖向剪力.设计时,钢-混间法向压力使接触面产生静摩擦力,作为第1道防线抗剪;极端状况下,即使连接面摩擦力失效产生滑移,剪力钉与锚杆仍可作为第2道防线,以“销栓”作用抗剪.根据上述分析可得,为了确保结构安全,验证以摩擦力承担外力的可靠性,以梁单元模拟剪力钉,从受力及相对位移两方面考虑,分析设计荷载工况下传剪机理和锚杆预应力及接触面摩擦系数变化对结构受力的影响.
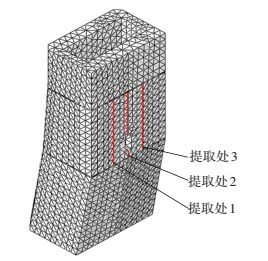
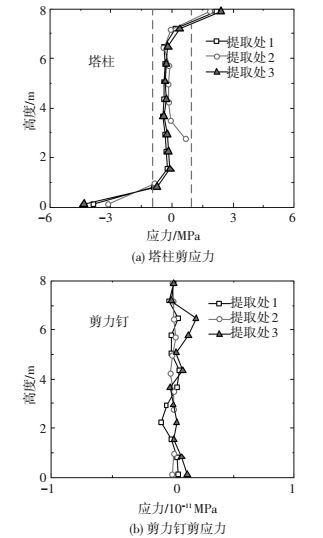
4.1 设计荷载工况下传剪机理研究最不利设计荷载工况(工况2)下剪力钉受力情况,提取如图 11所示位置处塔柱及剪力钉节点剪应力,做沿高度的剪应力分布如图 12所示,可知混凝土剪应力大部分区域均在1 MPa以内,剪力钉剪应力较小.可以看出竖向力主要由混凝土与钢横梁间摩擦力承担,摩擦力小于临界摩擦力.
|
图 11 应力提取处 Figure 11 Extraction position of the stress |
|
图 12 塔柱及剪力钉剪应力-高度曲线 Figure 12 Shear stress-height curves of pylon |
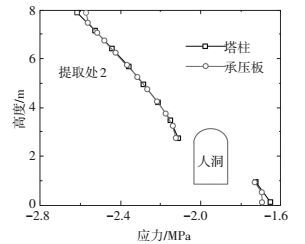
图 13为塔柱与承压板边侧与中心竖向位移-高度曲线,塔柱与钢横梁始终紧密相连,二者未发生相对滑动.由图 14中剪力钉正应力-高度曲线可知,由于锚杆预应力作用,剪力钉主要为受压,而剪应力非常小,因此表 5中剪力钉最大Von Mises应力主要为压力贡献.
|
图 13 塔柱及剪力钉竖向位移-高度曲线 Figure 13 Displacement-height curves of pylon and shear studs |

|
图 14 剪力钉正应力-高度曲线 Figure 14 Normal stress-height curves of shear studs |
研究锚杆预应力损失或减小锚杆张拉力对结构受力的影响,考虑最小张拉力为设计张拉力的10%,即最大预应力损失达90%,考察摩擦力抗剪能力,并与设计张拉力下计算结果进行比较,确定索塔锚固区抗剪安全储备.由于在正常使用状态下,要求钢横梁与混凝土间剪力钉最大滑移量限值为0.2 mm[15],因此定义当剪力钉钢-混相对滑移大于0.2 mm时,达到相对滑移状态,相对滑移曲线斜率增加为上一分析工况2倍,即滑移量明显增加时,达到临界滑移状态.
为研究仅由摩擦力抵抗竖向索力的能力,在节段模型中去除剪力钉,减小锚杆预应力,当塔柱与钢横梁间摩擦力不能抵抗竖向索力时相对滑移增大,滑移曲线斜率增加,达到临界摩擦力状态,并由锚杆承担一部分竖向剪力.
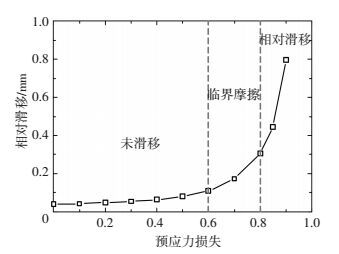
图 15为不同预应力损失时塔柱中心位置处(提取处2)塔柱与承压板平均相对位移.由图可知,随着预应力损失增加,塔柱与承压板相对滑移增加;预应力损失在60%以下时,相对滑移增加不明显,塔柱与承压板紧密贴合,摩擦力小于临界摩擦力;预应力损失达到60%时,滑移量增加,此时处于临界摩擦状态;当预应力损失在80%以上时,滑移量增加迅速,此时塔柱与钢横梁承压板已达到相对滑移状态.
|
图 15 不同预应力损失塔柱与钢横梁相对滑移 Figure 15 Relative slippage of pylon and steel box girder with different prestress loss |
由于预应力锚杆设置较多,且张拉力大,使锚固区在预应力损失60%时仍然能处于正常设计工作状态,结构具有足够的抗剪储备.
4.3 摩擦系数变化的影响研究接触面摩擦系数变化对结构受力的影响,参考文献[16]参数分析中取值,对摩擦系数进行逐级分析,通过初步分析,确定最小摩擦系数为0.08,塔柱与钢横梁产生较大滑移,因此摩擦系数分别取0.08、0.1、0.2、0.3、0.4,考察摩擦力抗剪能力,确定索塔锚固区抗剪安全储备.
图 16为不同摩擦系数下塔柱与承压板平均相对位移.由图可知,随着摩擦系数增加,塔柱与承压板相对滑移减小;摩擦系数在0.2以上时,相对滑移增加不明显,塔柱与承压板紧密贴合,摩擦力小于临界摩擦力;摩擦系数小于0.2时,滑移量增加,此时处于临界摩擦状态;当摩擦系数小于0.1时,滑移量增加迅速,此时塔柱与钢横梁承压板已达到相对滑移状态;摩擦系数小于0.08时,出现明显滑移.

|
图 16 不同摩擦系数塔柱与钢横梁相对滑移 Figure 16 Relative slippage of pylon and steel box girder with different friction coefficients |
为保证塔柱与钢横梁间主要以摩擦力抵抗竖向索力,工程中可采取一定的措施,提高塔柱与钢横梁承压板间粗糙度,增加结构的抗剪储备.
5 结论1) 有限元分析结果显示,除个别点应力集中外,各工况锚固区应力水平均远小于容许应力.混凝土塔柱最大压应力及最大拉应力未超过其设计值,结构具有足够的安全储备.
2) 钢锚箱前锚板存在较为明显的应力集中现象,这主要是由于锚垫板的面积较小,锚杆张拉导致锚杆孔附近产生较大的应力集中,此种状况可以通过增设锚垫板或扩大承压面积缓解.钢横梁隔板、承压板及横隔板最大应力不足容许应力1/2,可适当减小相应板厚避免工程浪费,在确保桥梁安全性的前提下节省造价.
3) 由于预应力锚杆作用,在最不利设计荷载工况(工况2)下,塔柱与钢横梁始终紧密相连,二者未发生相对滑动.钢横梁与塔柱间巨大静摩擦力作为第1道防线,承担钢横梁梁端主要剪力;若摩擦力失效,剪力钉与锚杆仍可作为第2道防线,提供类似“销栓”作用抗剪.
4) 锚杆预应力损失60%或接触面摩擦系数减小为0.2时,塔柱与钢横梁间剪力仍主要以摩擦力承担,结构具有足够的抗剪储备.
| [1] |
CAI H, AREFA J. Three-dimensional geometric nonlinear analysis of composite cable-stayed bridges using a refined double-beam model[J].
Journal of Bridge Engineering, 2014, 19(6): 04014017.
DOI: 10.1061/(ASCE)BE.1943-5592.0000579 |
| [2] |
ELOuni M H, KAHLA N B, PREUMONT A. Numerical and experimental dynamic analysis and control of a cable stayed bridge under parametric excitation[J].
Engineering structures, 2012, 45: 244-256.
DOI: 10.1016/j.engstruct.2012.06.018 |
| [3] |
BROWNJOHN J M W, LEE J, CHEONG B. Dynamic performance of a curved cable-stayed bridge[J].
Engineering structures, 1999, 21(11): 1015-1027.
DOI: 10.1016/S0141-0296(98)00046-7 |
| [4] |
GUEST J K, DRAPER P, BILLINGTON D P. SantiagoCalatrava's Alamillo Bridge and the idea of the structural engineer as artist[J].
Journal of Bridge Engineering, 2012, 18(10): 936-945.
DOI: 10.1061/(ASCE)BE.1943-5592.0000445 |
| [5] |
陈志华, 闫翔宇, 王小盾, 等. 慈海桥的新型斜拉桥和摩天轮复合结构体系[J].
土木工程学报, 2005, 38(12): 76-82.
CHEN Zhihua, YAN Xiangyu, WANG Xiaodun, et al. The hybrid structural system of new-type cable-stayed bridge and giant wheel in the CiHai Bridge[J]. China Civil Engineering Journal, 2005, 38(12): 76-82. DOI: 10.3321/j.issn:1000-131X.2005.12.013 |
| [6] |
BROWNJOHN J M W, XIA P Q. Dynamic assessment of curved cable-stayed bridge by model updating[J].
Journal of Structural Engineering, 2000, 126(2): 252-260.
DOI: 10.1061/(ASCE)0733-9445(2000)126:2(252) |
| [7] |
BAI Guangliang, TANG Guangwu, GOU Hongye. Experimental research and FEM analysis of steel corbel in pylon cable anchor zone of cable-stayed bridge [C]// International Conference of Logistics Engineering and Management. Chengdu: ICLEM press, 2010: 1248-1254.DOI: 10.1061/41139(387)171.
|
| [8] |
WOO J K, KYUNG S C. The design and construction ofGeogeum Grand Bridge [C]//The third International Symposium and Steel Structures. Seoul: ISSS press, 2005: 1-12.
|
| [9] |
张光辉, 张启伟, 刘玉擎, 等. 斜拉桥混合塔结合部受力机理模型试验[J].
哈尔滨工业大学学报, 2017, 49(3): 106-112.
ZHANG Guanghui, ZHANG Qiwei, LIU Yuqing. Model test of composite joint for tower of cable-stayed bridge[J]. Journal of Harbin Institute of Technology, 2017, 49(3): 106-112. DOI: 10.11918/j.issn.0367-6234.2017.03.017 |
| [10] |
LEE Y H, JOO Y T, LEE T, et al. Mechanical properties of constitutive parameters in steel-concrete interface[J].
Engineering Structures, 2011, 33(4): 1277-1290.
DOI: 10.1016/j.engstruct.2011.01.005 |
| [11] |
公路钢筋混凝土及预应力混凝土桥涵设计规范: JTG D62—2012 [S]. 北京: 中国建筑工业出版社, 2012.
Code for design of highway reinforced concrete andprestressed concrete bridges and culverts: JTG D62—2012 [S]. Beijing: China Architecture & building Press, 2012. |
| [12] |
郑舟军, 田晓彬, 余俊林, 等. 内置式钢锚箱索塔锚固区受力机理分析[J].
中国公路学报, 2010, 23(5): 84-89.
ZHENG Zhoujun, TIAN Xiaobin, YU Junlin, et al. Analysis of mechanical mechanism of pylon anchorage zones with built-in steel-anchor-box[J]. China Journal of Highway and Transport, 2010, 23(5): 84-89. |
| [13] |
张景峰, 李小珍, 肖林, 等. 混合梁斜拉桥钢-混结合段受力行为仿真分析[J].
西南交通大学学报, 2014, 49(4): 619-625, 699.
ZHANG Jingfeng, LI Xiaozhen, XIAO Lin, et al. Numerical simulation analysis of steel-concrete joint section in hybrid girder of cable-stayed bridge[J]. Journal of Southwest Jiaotong University, 2014, 49(4): 619-625, 699. DOI: 10.3969/j.issn.0258-2724.2014.04.009 |
| [14] |
刘沐宇, 万杰, 张强, 等. 剪力钉集束式与均布式布置下钢-混组合梁桥受力分析[J].
土木工程与管理学报, 2014, 31(3): 1-6.
LIU Muyu, WAN Jie, ZHANG Qiang, et al. Mechanical analysis of a steel-concrete composite girder bridge under cluster distribution and uniform distribution of the shear studs[J]. Journal of Civil Engineering and Management, 2014, 31(3): 1-6. DOI: 10.3969/j.issn.2095-0985.2014.03.001 |
| [15] |
白光亮. 大跨度斜拉桥索塔锚固区结构行为与模型试验研究[D]. 成都: 西南交通大学, 2009. DOI: 10.7666/d.y1689377.
BAI Guangliang. Study on the structural behaviors and experiments of anchorage zone of cable-stayed bridge [D]. Chengdu: Southwest Jiaotong University, 2009. DOI: 10.7666/d.y1689377. http://cdmd.cnki.com.cn/Article/CDMD-10613-2010115791.htm |
| [16] |
张煜, 阮欣, 石雪飞, 等. 斜拉桥钢-混锚板式索梁锚固区摩擦效应分析[J].
中南大学学报(自然科学版), 2013, 44(7): 2982-2988.
ZHANG Yu, RUAN Xin, SHI Xuefei, et al. Friction effects analysis of steel-concrete anchor plate in cable-beam anchorage zones of cable-stayed bridges[J]. Journal of Central South University (Science and Technology), 2013, 44(7): 2982-2988. |
 2017, Vol. 49
2017, Vol. 49


