2. 伊利诺伊大学香槟分校 农业与生物技术工程学院,美国 Illinois 61802
2. Department of Agriculture and Biological Engineering, University of Illinois at Urbana-Champaign, Illinois 61802, USA
浅层排水系统广泛存在于平原地区的集约化农田地域,尤其在美国中部地区,约70%的农田具有浅层排水系统[1],在中国的西北和江南地区也有不成规模的农田排水系统,该系统能够提高产量,但同时加速了污染物进入水体的速度[2].浅层排水系统存在的农田氮磷污染物的迁移过程一直是专家学者们关注的问题,美国学者开发了浅层排水水分垂直迁移过程模型DRAINMOD分析排水管网中水量的大小,并计算污染物流失量[3-6].但对于污染物在土壤层中迁移的微观过程并没有相应的研究和报道,国内学者对该问题的研究也处于初级阶段.本文利用有限元分析的方法[7-10],采用ANSYS有限元分析软件对包含浅层排水系统的土壤柱进行简化并进行数值仿真[11-12],进而分析土壤层中溶解性氮磷污染物的迁移过程及规律.
1 研究区域基本情况Little Vermilion River流域位于美国伊利诺伊州东部中心位置,流域中心坐标为(40°06′21.45″N, 87°41′34.12″W),是本研究的对象区域.该地区的土壤类型包括粉砂壤土(Drummer)和粉壤土(Flangan)[2],该地区特征实验点实测得到的初始条件如表 1所示.读取当地降雨重现期曲线,选取5 h降雨为基准,降雨强度为4 mm/h,同时保持该强度,将降雨历时提高到10~48 h,观察样方中氮磷迁移变化.
| 表 1 迁移过程初始条件与边界条件 Table 1 Initial and boundary condition of the transport process |
为简化计算,对样方进行相应假设,流化床的设计为重复对称结构,且在纵向延伸至无限远,所以,样方可以简化成切面二维模型.本文主要关注流化床内氮磷迁移的质量分数变化及迁移速度,因此,将降雨过程简化成初始流速,省略布水装置,通过计算等效水力传导率,简化了土壤分层过程计算量.大大降低计算难度,节省计算时间.出口处为压力出口,流体(进料、进水)进口处为速度入口,其余默认设为穿孔墙边界条件.
2 简化浅层排水土壤柱结构为了有效计算垂直方向迁移过程,利用有限元分析软件ANSYS©对选取的点迁移样方进行网格化,并通过求解边界条件的数值分析方法对网格内“三传”过程进行求解从而得到精确的迁移过程描述.首先,将土壤样方简化成土壤颗粒流化床,其中土壤粒径为平均粒径,流化床的设计如图 1所示.
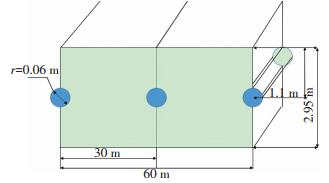
|
图 1 土壤流化床设计示意 Figure 1 Sketch of fluidized bed |
通过实测数据知土壤表层的硝酸盐、磷酸盐质量分数分别为20和0.3 mg/kg,进一步对样方进行近似,硝酸盐与磷酸盐均分布在表层20 cm土壤层内,池容量为无限大.首先研究5 h降雨过程中土壤层中硝酸盐质量分数的变化,由图 2可以看出,降雨5 h后,排水管线中并没有渗流水分流入及硝酸盐质量分数变化发生.
但在地表到浅层排水管处,质量分数已经发生变化,质量分数分层过程也符合水位降曲线.由于土壤等效水力传导率低于降雨速率,对迁移过程造成额外压力,水流趋向于在浅层排水管上方形成快速渗透区.这也是浅层排水能够快速排出累积在农田的多余水分的原因,同时,由于该驱动力的存在,土壤中硝酸盐也产生了浓差,如图 2所示.在同一水平线5 h降雨后最大浓差2 mg/kg,但5 h降雨及4 mm/h降雨强度所产生的驱动力依然不足以使得水分到达排水管,水分只向下运动了33.5 cm.由于土壤也含有水分,界面质量分数差则是传质过程驱动力,传质速率由浓差及传质系数决定,但此时降雨停止,减少了压力,水分的运动只能通过重力作用,迁移过程也将减慢.
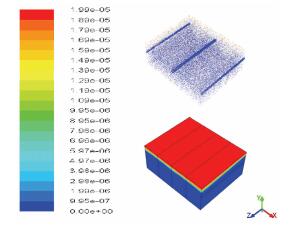
|
图 2 降雨5 h硝酸盐5 h后点垂直方向质量分数变化 Figure 2 Vertical nitrate concentration change in soil after 5 h rainfall event |
5 h降雨停止后,随着重力作用,水分继续向下迁移,24 h后硝酸盐开始出现在排水管中,其质量分数为3.99~4.99 mg/kg.由于有坡度存在,远处依然有排水管没有水分流入,但只是理论上的情况,实际情况中并没有无限远的管道存在,因此,管体将全部接收排水.由图 3可以看出,24 h后,由于降雨历时只有5 h,质量分数差有明显的分层,因为在24 h内随着水分的重力下渗并伴随着水分被不饱和土壤吸收,水分向下迁移的速度不断减慢,这为传质过程提供了足够的时间和空间,使得质量分数分层现象明显,而且质量分数分布也与地下水位的趋势相同,在具有浅层排水管的位置水位出现下降,而在无排水管位置层呈现均匀分布趋势,因此,在两条管线直接地下水位呈现“拱形”.而质量分数的分布也与水分分布规律相同.
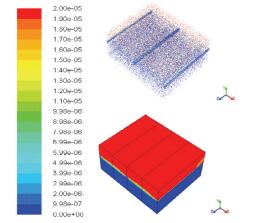
|
图 3 降雨5 h硝酸盐24 h后点垂直方向质量分数变化 Figure 3 Vertical nitrate concentration change in soil after 24 h rainfall event |
当整个过程持续48 h后,硝酸盐质量分数分布如图 4所示.随着时间的推移,由于无持续水分的输入,上层土壤质量分数无进一步的扩散变化,下层土壤随水分重力下渗,使得质量分数分层被压缩,但由于水量小,压缩效果并不明显.质量分数分布基本与24 h后接近,并无显著变化,而管内质量分数为4~5 mg/kg.
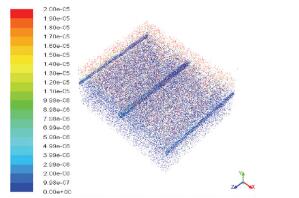
|
图 4 降雨5 h硝酸盐48 h后点垂直方向质量分数变化 Figure 4 Vertical nitrate concentration change in soil after 48 h rainfall event |
在5 h降雨结束后,磷的质量分数分布趋势与硝酸盐类似,因为溶解态磷酸盐在迁移过程上与溶解态硝酸盐并无差异.在初始质量分数为非饱和溶液的条件下,磷酸盐在降雨发生后主要发生的迁移为传质过程,其中溶解过程是限制步骤,由图 5可以看出,磷酸盐在降雨5 h后的质量分数分布,相对于硝酸盐分布较密集,这是由溶解速度慢造成的,而质量分数降低的位置依然与硝酸盐类似,出现在浅层排水管设置位置,但由于磷酸盐初始质量分数较低,在图内颜色差异较大,但实际最大浓差仅为0.01 mg/kg.但该种分析过程并不能体现溶解过程,对于磷酸盐这种微溶的物质,传质现象在短时间内并不明显.水分也同样没有到管,水分到管时间理论上与硝酸盐相同.当水分到管时,磷酸盐的浓差将比硝酸盐更大,也是由溶解度低造成的.
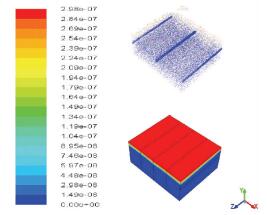
|
图 5 降雨5 h磷酸盐5 h后点垂直方向质量分数变化 Figure 5 Vertical phosphate concentration change in soil after 5 h rainfall event |
如图 6,经过24 h的传质过程后,浓差的分层加大,最大浓差为0.2 mg/kg,管内质量分数为0.03 mg/kg.经过48 h的渗透过程后,磷酸盐的质量分数分布基本与24 h后类似,只是浓差进一步扩大,这与硝酸盐迁移过程类似.在无进一步的水分输入后,水分通过重力作用向下运动,但速度会不断减慢,这是由于下层土壤的不饱和度高于上层,土壤的张力更大,吸水性更强,使得水分更不易于向下迁移,从而浓差开始被压缩.但由于初始质量分数不高,造成传质速率不高,从而导致浓差压缩过程不明显,依然保持与24 h后的状态接近,从而随着所有能够到管并排走的水分都排走后,土壤中磷酸盐的迁移将停滞在无水分运动之后.同时伴随转化过程的发生,在迁移过程中虽然也伴随着转化,但由于时间较短,转化所造成的影响相对较小,但在迁移过程停滞后,转化起到主要作用,其中包括土壤中有效磷与稳态磷的动态平衡过程,有效磷和溶解态磷之间的动态平衡过程,磷的各个形态的相互转化,土壤中微生物吸收作用等,以上作用导致了磷酸盐迁移的停滞,但转化不包括在本研究的讨论中.
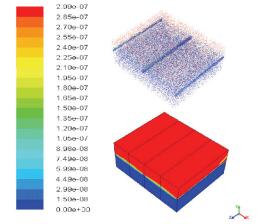
|
图 6 降雨5 h磷酸盐24 h后点垂直方向质量分数变化 Figure 6 Vertical phosphate concentration change in soil after 24 h rainfall event |
进一步分析图 7(a)、(b)、(c),在10 h降雨结束后,管内已经出现质量分数变化,管内的质量分数为5~6 mg/kg,此时最大浓差达8~9 mg/kg.在没有达到最大质量分数的土壤层中,浓差也明显高于5 h降雨过程,这是由降雨量不同直接造成的结果.流量直接影响了硝酸盐的迁移,而且流量越大加速了硝酸盐的迁移.流量的增加与硝酸盐的迁移并不是线性关系,因为硝酸盐的易溶性,在流失量的层面上限制条件为流失通量,在降雨量增大后,饱和土壤的透水性要明显大于不饱和土壤,因为在排空土壤毛细孔内空气后,同时由于浅层排水管的作用,饱和土壤的水渗透只是取决于土壤粒径,土壤粒径越大透水速度越快,因此,在土壤饱和后硝酸盐的流失通量将达最大值.
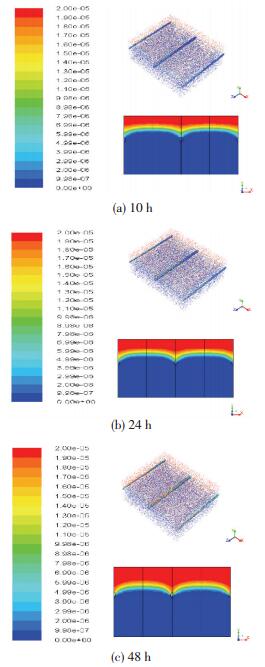
|
图 7 降雨10 h硝酸盐10、24、48 h后点垂直方向质量分数变化 Figure 7 Vertical nitrate concentration change in soil after 10, 24, 48 h for 10 h rainfall event |
24 h后管内质量分数持续增大,达8~9 mg/kg,最大浓差为13~14 mg/kg,因为降雨较之前增加1倍,增加了硝酸盐的迁移.图 7(c)为48 h后质量分数分布,可以看出,管内质量分数已达14~15 mg/kg,最大浓差也达15~16 mg/kg,通过观察动态变化过程,在30 h后管内质量分数分布基本稳定在该状态,并持续至48 h.
对于10 h降雨过程磷酸盐的迁移过程如图 8(a)、(b)、(c)所示,其质量分数变化过程与硝酸盐并无显著差异,变化趋势类似,主要差别在于磷酸盐迁移过程的限制步骤为溶解及传质过程,溶解度低且浓差低是造成磷酸盐迁移慢的主要原因,但如果水量充分,时间足够,在最终分布形式上磷酸盐的样式应与硝酸盐相同.
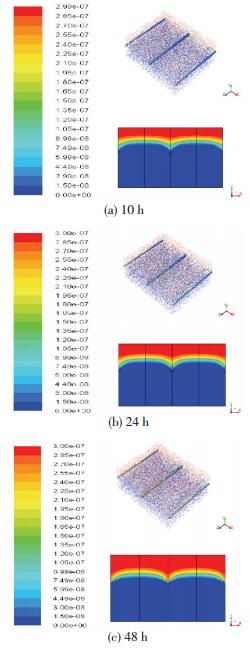
|
图 8 降雨10 h磷酸盐10、24、48 h后点垂直方向质量分数变化 Figure 8 Vertical phosphate concentration change in soil after 10, 24, 48 h for 10 h rainfall event |
进一步观察48 h连续降雨过程后氮磷迁移过程,图 9为硝酸盐在48 h、4 mm/h降雨过程中,0、5、24、48 h后质量分数的分布状况.可以看出,在连续降雨过程中,硝酸盐的迁移随时间不断增大,直至达到最大质量分数,在24 h内已经有最大质量分数在管内出现,说明硝酸盐的迁移过程直接与流量相关,流量越大迁移量越大,迁移过程直接符合水分迁移过程.
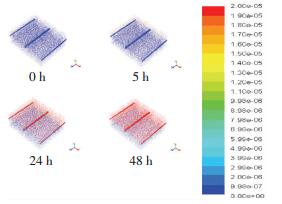
|
图 9 48 h连续降雨中硝酸盐迁移过程 Figure 9 Nitrate transport pattern after 48 h continuous rainfall event |
为了体现硝酸盐与磷酸盐在垂直方向上迁移过程的不同, 将质量分数分布标尺设置与硝酸盐一致(以大质量分数范围为准).由图 10可以看出,在0、5、24、48 h的迁移过程中,磷酸盐在质量分数层面的变化并不显著,但溶解的磷酸盐的迁移也随同水分迁移规律,磷酸盐的垂直迁移过程不只取决于流量大小.其迁移也由降雨时间、初始池溶解态磷质量分数、有效磷含量、施肥时间等多种因素决定,因此,磷随水分流失过程是磷迁移途径中不显著的一部分.正是因为磷的不易溶性,多以稳定态存在,大量磷的迁移则是由吸附在土壤颗粒的多种磷形式随泥沙迁移过程中产生,并伴随吸附解析、溶解溶出、水解化合等作用,最终进入水体,因此,本研究只关注溶解态的磷迁移过程.进一步讨论在浅层排水管中,两种物质的质量分数随时间变化过程,结果如图 11所示.在持续降雨过程中,硝酸盐最快在6 h后到达管内,6~18 h在持续的水分输入下,质量分数呈指数增长趋势,18 h后质量分数达到稳定增长状态,并超过20 mg/kg,48 h计算结束.如果继续计算,没有排出的多余水分在重力作用下将持续渗出,质量分数会在某一时刻达到峰值,然后再不断随水量减少,传质过程的驱动力减弱,入管质量分数不断下降,最终停止.而磷酸盐的迁移能力相对硝酸盐低得多,首先,活性磷在土壤中的比例相对较低,再加上溶解过程缓慢等原因使得磷酸盐在垂直迁移过程不显著.
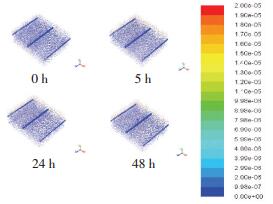
|
图 10 48 h连续降雨过程中磷酸盐迁移过程 Figure 10 Nitrate transport pattern after 48 h continuous rainfall event |
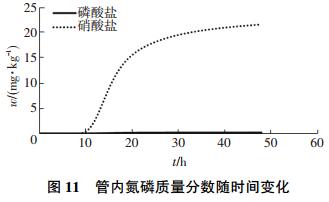
|
图 11 管内氮磷质量分数随时间变化 Figure 11 Nitrate and phosphate concentration variation along with the time |
1) 在空间迁移过程点层面垂直迁移途径中,在短时间降雨事件,氮磷随水分渗透过程的形式一致,但表现出不同的特征.氮迁移的主要形式为硝酸盐形态,硝酸盐溶解度大,在雨量不断增大过程中,硝酸盐迁移量呈指数增长趋势,直至水量输入输出平稳后,硝酸盐迁移量也达到平稳.
2) 磷的迁移形态为溶解态磷酸盐,磷酸盐的溶解度低,磷各种形态的平均吸附系数高,因此,需要一定的水量才能打破磷酸盐的水解平衡态,导致磷酸盐迁移量及速度较硝酸盐慢.
3) 浅层排水管网中,氮磷质量分数的变化与土壤层中的变化过程相近,但在水分没有渗透到排水管网土层时,管网内氮磷质量分数并没有变化,在降雨量适中时,氮磷的质量分数在管网中都呈线性增加的趋势,而当水量进一步增大时,氮的质量分数呈现指数增加,而磷的流失质量分数依然为线性增加.
| [1] | ALEXANDER R B, SMITH R A, SCHWARZ G E, et al. Differences in phosphorus and nitrogen delivery to the gulf of Mexico from the Mississippi river basin[J]. Environ Sci Technol, 2008, 42 (3) : 822-830. DOI: 10.1021/es0716103 |
| [2] | KALITA P K, COOKE R A C, ANDERSON S M, et al. Subsurface drainage and water quality: The Illinois experience[J]. Trans ASABE, 2007, 50 (5) : 1651-1656. DOI: 10.13031/2013.23963 |
| [3] | BROWN R A, SKAGGS R W, HUNT W F. Calibration and validation of DRAINMOD to model bioretention hydrology[J]. J Hydrol, 2013, 486 : 430-442. DOI: 10.1016/j.jhydrol.2013.02.017 |
| [4] | ALE S, GOWDA P H, MULLA D J, et al. Comparison of the performances of DRAINMOD-NII and ADAPT models in simulating nitrate losses from subsurface drainage systems[J]. Agric Water Manage, 2013, 129 : 21-30. DOI: 10.1016/j.agwat.2013.07.008 |
| [5] | TIAN S Y, YOUSSEF M A, SKAGGS R W, et al. DRAINMOD-FOREST: Integrated modeling of hydrology, soil carbon and nitrogen dynamics, and plant growth for drained forests[J]. J Environ Qual, 2012, 41 (3) : 764-782. DOI: 10.2134/jeq2011.0388 |
| [6] | SKAGGS R W, YOUSSEF M A, CHESCHEIR G M. A drainmod-based method to estimate effects of drainage water management on annual nitrogen loss to surface water[J]. Trans ASABE, 2012, 55 (3) : 799-808. DOI: 10.13031/2013.41515 |
| [7] | MOHSIN R, MAJID Z A, YUSOF M Z. Safety distance between underground natural gas and water pipeline facilities[J]. Reliab Eng Syst Safe, 2014, 131 : 53-60. DOI: 10.1016/j.ress.2014.06.008 |
| [8] | DAI Z L, HUANG Y, CHENG H L, et al. 3D numerical modeling using smoothed particle hydrodynamics of flow-like landslide propagation triggered by the 2008 Wenchuan earthquake[J]. Eng Geol, 2014, 180 : 21-33. DOI: 10.1016/j.enggeo.2014.03.018 |
| [9] | NGUYEN T P O, HELBLING D E, BERS K, et al. Genetic and metabolic analysis of the carbofuran catabolic pathway in Novosphingobium sp KN65.2[J]. Appl Microbiol Biot, 2014, 98 (19) : 8235-8252. DOI: 10.1007/s00253-014-5858-5 |
| [10] | YANG X F, RICHMOND M C, SCHEIBE T D, et al. Flow partitioning in fully saturated soil aggregates[J]. Transport Porous Med, 2014, 103 (2) : 295-314. DOI: 10.1007/s11242-014-0302-y |
| [11] | HU D W, LI L, LIU H, et al. Design and control of rotating soil-like substrate plant-growing facility based on plant water requirement and computational fluid dynamics simulation[J]. Ecol Eng, 2014, 64 : 269-275. DOI: 10.1016/j.ecoleng.2013.12.048 |
| [12] | HONG S W, LEE I B, SEO I H, et al. Measurement and prediction of soil erosion in dry field using portable wind erosion tunnel[J]. Biosyst Eng, 2014, 118 : 68-82. DOI: 10.1016/j.biosystemseng.2013.11.003 |
 2017, Vol. 49
2017, Vol. 49


