影响供水管道漏失[1]的因素很多,可分为外因和内因.外因亦称为人为因素,如施工损坏、人为破坏等.由于人为因素没有一定的规律可循,很难做出统计并得到结论,因此,建立供水管网渗漏模型时应当排除外因影响.内因是指管网特性及周围环境的影响,如管径、压力、埋深等.内因中除了压力外,其他因素对于特定管网系统已是定值,因此,控制漏失时,应将主要方向放在压力控制上[2].目前,管网渗漏预测模型主要有两大类:点式渗漏模型和一致渗漏模型[3].相比点式渗漏模型,一致渗漏模型更接近管网日常工作状况,因此,目前一致渗漏模型被普遍采用.一致渗漏模型应用了单漏点漏损指数模型,是在假定管网各部分的渗漏水平一致的前提下,建立管段的渗漏流量与管网的总体渗漏水平之间所满足的水力关系.中国的传统水力模型是假定节点用水量为定值并将总漏失量在管网中平均分配,但实际上用水量是压力的函数,管网压力不同,漏失亦不同.因此,传统水力模型不利于管网漏失的预测控制工作,模型模拟结果与管网实际运行工况差距较大,指导性、预测性较差.为此,本文对传统水力模型进行校正,运用一致渗漏模型思想,即将管段的漏失量按管段长度分配,构建压力驱动节点流量的水力(PDD)模型,并在此基础上对压力控制漏失技术进行分析研究.
1 PDD模型压力驱动节点流量模型自20世纪80年代提出以来,国内外诸多学者对此做了相关研究.Germanopoulos等[4]将与压力有关的泄漏因素引入模型中,Ligget等[5]提出了基于压力和流量的相关性分析方法.国内在基于压力和(或)流量分析方面还在试验与理论探讨过程中[6],王俊良等[7]在压力驱动节点流量水力模型基础上引入漏失量最小化的目标函数,建立了压力驱动节点流量漏失控制模型.高金良等[8-11]按照流量-水头关系的不同得到了不同的压力驱动节点流量模型并对此所处了较为深入的研究.
传统供水管网的微观水力模型不区分节点流量类别,将用户用水量与漏失水量统一为节点流量,并将所有水量依据管段的长度分配到各个节点,这种模型忽略了用户用水量在一定压力下不随压力变化而漏失量是会随着供水压力变化的特性,可以视为流量驱动节点流量模型.压力驱动节点流量模型则将节点流量区分对待[12],考虑供水管网中节点漏失流量与供水压力相互影响的特性,将漏失流量和其他基于压力的流量的关系嵌入水力模型中,从而使水力模拟更加符合实际情况,进而可对供水管网进行漏失等级评价.
本文将传统水力模型中的用水量划分为用户用水量和漏失量,其中用户用水量不随压力改变,而漏失量随压力改变.根据一致渗漏模型思想,建立漏失量与压力的指数关系式,构建改进的PDD模型,并应用于Y市实际管网,分析其供水状况,进行管网漏失控制分析.
供水管网中的漏失通常是发生在管段上的,因此,可建立管段漏失量与管段压力的关系模型,即
| $ {{q}_{k-\text{leak}}}=\left\{ \begin{array}{*{35}{l}} {{\beta }_{k}}{{l}_{k}}{{\left( {{p}_{k}} \right)}^{{{\alpha }_{k}}}}, & {{p}_{k}}>0, \\ 0, & {{p}_{k}}<0. \\ \end{array} \right. $ | (1) |
式中:qk-leak为k管段的漏失量;α, β为漏失系数;lk为k管段长度;pk为k管段的平均压力.
供水管网建模的过程中,流量通常是加在节点上的,因此,需要将管道漏失量等价为节点漏失量,节点漏失量等于与该节点连接管段漏失量之和的一半,故该模型为
| $ {{q}_{i-\text{leak}}}=\sum\nolimits_{k}{\frac{1}{2}{{q}_{k-\text{leak}}}=\frac{1}{2}}\sum\nolimits_{k}{\beta {{l}_{k}}{{\left( {{p}_{i}} \right)}^{\alpha }}.} $ | (2) |
式中:qi-leak为节点i的漏失量;pi为节点i的自由水头.
漏失量的计算需要定出α,β的值,通常α的值与漏失类型有关,取决于管道材质; β的值与单位长度管段的漏失数量有关,需要通过该建模区域历史漏失数据计算得出.此时,总节点流量为
| $ {{q}_{i-\text{act}}}={{q}_{i-\text{use}}}+{{q}_{i-\text{leak}}}. $ | (3) |
式中:qi-act为节点i的实际用水量;qi-use为节点i的用户用水量.
2 PDD模型控制漏失的建模过程 2.1 收集、整理与评估供水管网基础数据城市供水管网水力建模基础信息可分为静态信息和动态信息[13].静态信息是指供水管网的特性数据,如管径、管材、拓扑结构等;动态信息是指供水管网的运行数据,如调度信息、水泵运行参数等.这些数据主要来源于基础的统计数据和现场实测.
基础的统计数据大多可以从各地区自来水公司建立的该城市供水管网的GIS系统(地理信息系统)和SCADA系统(数据采集与监视控制系统)中直接导出,少量这两个系统不包括的建模数据可以从水厂以及泵站的调度信息记录中获取.基础的统计数据调查范围包括供水管网、水厂和用户3个部分.部分供水管网参数会随着使用年限而改变,无法从基础数据中得到,需要在现场对供水管网的部分参数进行实际测量,以满足供水管网微观水力模型的精确化要求.需要现场实测的主要有干管摩阻系数测试、大用户用水变化曲线测试和压力测试.
供水管网的建模过程收集得到的各类数据普遍存在数据量大、数据矛盾、数据异常、数据短缺等现象,这些原始数据无法直接导入模型,需要对收集的数据进行规范化的整理与评估,分析得到有效的运行数据,进行供水管网建模[14].
2.2 建立供水管网传统水力模型建立供水管网传统水力模型是结合现实供水管网的数据构建能量方程和连续性方程,并求解这两个方程的过程.具体步骤如下:输入供水管网静态信息和动态信息;构建能量方程组和连续性方程组;对能量方程和连续性方程进行联合求解,求出节点压力、管段水头损失等;模型校核.本课题采用PDD模型,即在传统水力模型基础上的改进模型,因此,在构建传统水力模型阶段不进行校核,待PDD模型构建完成后,再进行PDD模型的校核.
2.3 计算供水管网的漏失系数在供水管网传统水力模型的基础上,为每个节点添加漏失系数,可得到压力驱动节点流量水力(PDD)模型.如式(2)所示,管网的α、β值是反映供水管道特定时期特性的参数,其只与管道本身性质有关,不随管网运行工况等外界因素而变化,是管龄、管长、管材、施工条件等特性的综合反映值,它们是动态变化的,管道性质改变时,其值也随之改变.α的取值范围通常为[0.5,2.5],本文统一取被普遍认可的经验值1.18,β值则需通过历史漏失率计算得到.本文所建模型中,每个节点的漏失水量还与节点连接的管段长度有关.因此,供水管网漏失系数的计算是一个单变量非线性优化问题,变量为β,优化目标为计算漏失量和实际漏失量之差,当二者之差的绝对值最小时(即计算漏失量与实际漏失量相等)β取1,当二者之差的绝对值最大时(此时计算漏失量为0)β取0,所以,β的值必然落在区间(0, 1)上,可以通过循环迭代收缩区间的方法求解该问题.
2.4 实现PDD漏失模拟用扩散器实现漏失模拟,定义节点扩散器流量为
| $ q=C{{p}^{r}}. $ | (4) |
式中:q为扩散器流量,L/s, 可用于模拟节点漏失流量;C为扩散器系数;p为节点压力, m;r为压力指数,本文中该值通常取1.18.
求得β值后,结合连接节点管段的长度,计算出各个节点的扩散器系数C值,然后将C值赋到各个节点的属性值中.并且将传统水力模型的用户用水量根据实际漏失量等比例减少,这样得到的PDD模型总水量与传统模型一致,但增加了供水管网节点的漏失流量,并且该漏失流量根据节点压力而变化.
2.5 模型校核建模过程中影响模型精度的主要因素有基础数据的准确性[15]、管道摩阻系数取值的不确定性[15]、水泵特性曲线的不确定性、节点流量不确定性和随机性及供水管网人工操作不确定性等.建模完成后,以实测数据(如流量、压力、摩阻系数、水泵特性曲线等)为基础,对模型进行校验,有重大异常时,完善管网图形,核实基础数据的准确性;当无重大异常时,调整节点流量和管段的海森威廉系数,直到满足模型精度要求方可应用.
3 算例以Y市实际管网的基础资料建立PDD模型,对其供水状况进行分析,证明该方法可以用于中国城市供水管网漏失控制的工作中.
3.1 建立Y市传统水力模型Y市市区部分面积100 km2,总人口数约50万,地势平坦,地势最大高差20 m左右.水厂主要由两座水厂、300 km供水管线及1 022个阀门等构筑物组成.水厂实际总供水量约22万m3/d.现供水系统配有SCADA系统及GIS系统.DN200以上水表均为电子流量计计量,抄表到户的用户约为7 000户.从GIS系统中导出Y市基础高程、管长、管径、管网拓扑等信息,并将其转化为标准的供水管网建模数据库的格式,管网统计数据如表 1.
| 表 1 GIS数据导出数据量统计 Table 1 Data statistics exported in GIS |
选取一个月中用户抄表数据,由大到小排列用水量,确定大用户.该模型的大用户确定依据为所有大用户的用水量占全管网总抄表水量的60%以上.结合实测的大用户日用水变化曲线,计算出各个时刻大用户用水量,将其输入到相应节点.整个供水区域各个时刻的总水量均可从SCADA系统中得出,此时减去各时刻计算出的大用户用水量,将剩下的水量均分到其他节点.供水管网入口处压力和流量信息取自SCADA系统,供水管段的海森威廉系数按照实测值导入,没有实测管段的海森威廉系数按照实际调查的管段材质和铺设年代给出.最后将水源与泵站信息导入到模型中,实现供水管网水力模型的计算.
3.2 建立Y市PDD模型实现漏失模拟上述得到的是未经校核的传统供水管网水力模型,现在将该水力模型各个节点流量划分为用户用水量和漏失量,其中漏失量随节点压力改变,而用户用水量不随节点压力改变.用节点扩散器能够实现该功能,从而达到模拟漏失的目的.
PDD模型中节点漏失的定义如式(2),则整个管网的漏失量为
| $ {{q}_{\text{T-leak}}}=\sum\nolimits_{i}{{{q}_{i-\text{leak}}}=\beta }\sum\nolimits_{i}{\left( \frac{1}{2}\sum\nolimits_{k}{{{l}_{k}}p_{i}^{\alpha }} \right).} $ | (5) |
式中qT-leak为整个供水管网总的漏失流量.
实际供水管网中瞬时的漏失流量无法测得,因此, 在建模时运用平均漏失流量数据替代.实际供水管网中的平均漏失流量可通过月抄表数据统计得到,如式(6).可采用选定的模型校核日的当月抄表数据.
| $ {{q}_{\text{act-leak}}}=\frac{{{Q}_{\text{T}}}-\sum\nolimits_{i}{{{Q}_{i-\text{ser}}}}}{3.6\times 24t}\times \gamma . $ | (6) |
式中:qact-leak为月实际平均漏失流量,L/s;QT为月总供水量,m3;Qi-ser为用户月用水量,m3;t为供水公司抄表时间间隔,d;γ为产销差系数,用于估计实际漏失流量.
从而可建立如下方程:
| $ \begin{align} & {{q}_{\text{T-leak}}}=\beta \sum\nolimits_{i}{\left( \frac{1}{2}\sum\nolimits_{k}{{{l}_{k}}p_{i}^{\alpha }} \right)}=\frac{{{Q}_{\text{T}}}-\sum\nolimits_{i}{{{Q}_{i-\text{ser}}}}}{3.6\times 24t}\times \gamma = \\ & {{q}_{\text{act-leak}}}. \end{align} $ | (7) |
式中:α取值1.18,lk属于水力模型中的基础数据,pi可通过水力计算求出,仅有一个未知数β,其他参数均可知.但由于节点流量和压力相互影响,β值改变时,pi也会随着改变,可构造适应度函数进行计算.适应度函数等于总计算供水量减去总实际供水量,优化目标是使适应度函数尽可能接近零.计算步骤如下:
1) 统计一个月的用户用水及总表数据计算出漏失率L;
2) 原水力模型中所有节点流量乘以(1-L);
3) 计算所有节点连接的管段长度和的一半,并构建矩阵A;
4) 构造fitness适应度函数,函数变量为β,函数值为计算供水量减去实际供水量;
5) 构造方程fitness (β)=0;
6) 运用二分循环迭代法求解该方程,计算出β值;
7) 矩阵A乘以β即为每个节点的扩散器系数,将其赋值到模型中.
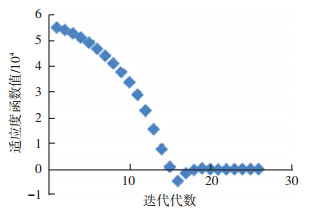
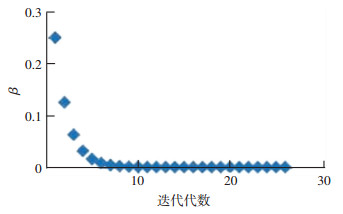
图 1、2为二分法迭代过程中,适应度函数值和β值随迭代代数的变化,可以看出,大约计算了18代时,适应度函数值已接近0,最终计算得β为2.755 294×10-5.
|
图 1 适应度函数随迭代代数的变化值 Figure 1 Fitness function value changes with the iterative algebra |
|
图 2 β随迭代代数的变化值 Figure 2 β value changes with the iterative algebra |
PDD漏失模拟模型构建完成后,需要对模型进行校核,即依据供水管网中安装的压力表的实时测量值对供水管网模型进行调整,调整模型中未经实测管段的海森威廉系数值,从而使模型符合国内模型精度评价通用标准[16].
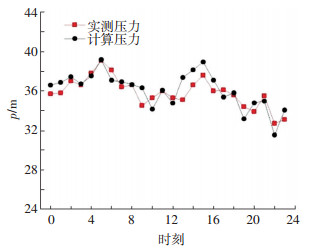
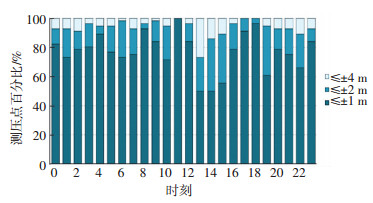
Y市供水管网中共安装了56个压力监测表.首先以选定的模型校核日数据中11时的压力数据作为模型校核基准点,调整模型各参数.以该日数据进行24 h动态校核.本文仅列举01号压力监测表的校核结果数据,如图 3所示.所有节点各时刻校核结果统计数据如图 4所示,各测压点24 h误差范围统计详见表 2.
|
图 3 01号压力监测点实测值与计算值对比 Figure 3 Measured and calculated values of No.01 pressure monitoring point |
|
图 4 测压点24 h计算值与实测值误差分布 Figure 4 Error distribution of calculated and measured values for 24 h |
| 表 2 各测压点24 h误差范围统计 Table 2 Pressure measuring point error range statistics for 24 h |
由图 4和表 2可以看出,该PDD模型与实际供水管网运行压力情况吻合良好,测压点误差满足水力模型校核标准,可以进行管网漏失控制研究及评估.
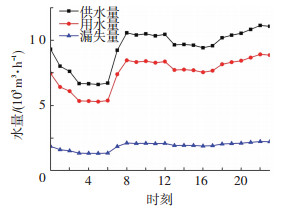
校核后的延时水力模拟模型计算得出5点和22点分别为全天供水的最低时和最高时,全天供水量变化趋势见图 5.全天出厂扬程变化见图 6.全天平均时刻供水流量为9 373 m3/h,16时的供水流量为9 416 m3/h,最接近全天平均时刻用水.
|
图 5 全天各时刻水量 Figure 5 Each moment water throughout the day |
|
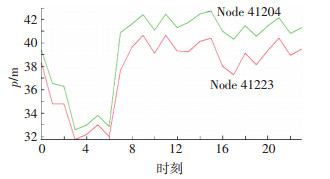
图 6 各时刻出厂扬程 Figure 6 Each moment factory head for water source |
1) 在传统模型的基础上,将节点流量划分为用户用水量和漏失量,建立漏失与压力的指数关系式,改进了一致漏损模型,完成了对传统水力模型的校正,获得更加接近管网实际工况的节点流量和节点压力,证实了压力驱动节点流量模型控制漏失方法的实用性.提出构造适应度函数并运用二分迭代法法求解PDD模型的方法,并应用于Y市实际管网,该模型能够模拟供水管网漏失,从而更接近供水管网实际运行情况,可用于指导管网分区等.
2) 供水管网建模过程中数据收集以及数据规范化录入是工作量最大的部分,时长占整个过程的80%以上,这一步骤处理的好坏直接影响之后建模以及优化的效率.实际工程中,可通过夜间最小流量对式(2)中各小区的α值进行优化,从而使漏失模型更加准确.本文的PDD模型中的实际漏失是通过产销差数据乘以系数得到,虽然可以控制漏失,这种方式与真实漏失依旧存在差距,建议可运用水平衡表计算真实漏失,使模型更加精准.针对不同的管材和埋设条件等选择不同的漏失系数,进一步改进一致漏损模型,会得到更加符合实际管网运行工况的模型,这也正是致力研究的课题.
| [1] | BECCIU G, MAMBRETTI S, MARTINS P S. Evolutionary optimization for water losses recognition in water supply networks[J]. European Journal of Environmental and Civil Engineering, 2015, 19 (8) : 976-999. DOI: 10.1080/19648189.2014.988295 |
| [2] |
张敏.城市供水管网基于压力驱动节点流量模拟漏失控制的研究[D].哈尔滨:哈尔滨工业大学, 2009:51-54.
ZHANG Min. Simulation leakage control research for urban water supply network based on the research of pressure-drive node flow simulation leakage control[D]. Harbin: Harbin Institute of Technology, 2009:51-54. |
| [3] |
陈玲俐, 李杰. 供水管网渗漏分析研究[J].
地震工程与工程振动, 2003, 23 (1) : 115-118.
CHEN Lingli, LI Jie. Leakage analysis of water supplying network[J]. Earthquake Engineering and Engineering Vibration, 2003, 23 (1) : 115-118. |
| [4] | GERMANOPOULOS G, JOWITT P W. Leakage reduction by excess pressure minimization in a water supply network[J]. ICE Proceedings, 1989, 87 (6) : 195-214. |
| [5] | VITKOVSKY J P, LIGGETT J A, SIMPSON A R, et al. Optimal measurement site locations for inverse transient analysis in pipe networks[J]. Journal of Water Resources Planning and Management, 2003, 129 (6) : 480-492. DOI: 10.1061/(ASCE)0733-9496(2003)129:6(480) |
| [6] |
董深, 吕谋, 盛泽斌, 等. 基于遗传算法的供水管网反问题漏失定位[J].
哈尔滨工业大学学报, 2013, 45 (6) : 106-107.
DONG Shen, LU Mou, SHENG Zebin, et al. Inverse transient leakage location of water supply network based on genetic algorithm[J]. Jouranl of Harbin Institute of Technology, 2013, 45 (6) : 106-107. |
| [7] |
王俊良, 李娜娜, 高金良, 等. 基于压力驱动节点流量模型的供水管网漏失控制[J].
中国给水排水, 2010, 26 (13) : 106-108.
WANG Junliang, LI Nana, GAO Jinliang, et al. Leakage control of water distribution system based on pressure-driven node flow model[J]. China Water & Wastewater, 2010, 26 (13) : 106-108. |
| [8] |
涂敏.供水管网在线监测漏失定位模型研究[D].哈尔滨:哈尔滨工业大学, 2012:7-22.
TU Min. Research on online monitoring and leak location model in water distribution system[D]. Harbin: Harbin Institute of Technology, 2012:7-22. |
| [9] |
张飞凤.供水管网优化压力控制漏失研究[D].哈尔滨:哈尔滨工业大学, 2012: 13-23.
ZHANG Feifeng. Research on optimal pressure of water distribution system for leakage control[D]. Harbin: Harbin Institute of Technology, 2012: 13-23. |
| [10] |
陈晨.多水源供水系统泵组优化控制漏失[D].哈尔滨:哈尔滨工业大学, 2012: 5-10.
CHEN Chen. Leakage control of multi-source water distribution system by optimal pump schedule[D]. Harbin: Harbin Institute of Technology, 2012: 5-10. |
| [11] |
张继昌. D市多水源供水管网系统水源事故时优化调度研究及应用[D].哈尔滨:哈尔滨工业大学, 2011: 7-9.
ZHANG Jichang. Research and application on optimal operation of D city's multi-source water distribution system when source accident[D]. Harbin: Harbin Institute of Technology, 2011: 7-9. |
| [12] | WU Z Y, BURROWS R, M00RCROFT J, et al. Pressure-dependent leakage detection method compared with conventional techniques[C]// WDSA 2010. EWRI, Am: ASCE, 2010: 1083-1092. |
| [13] |
赵洪斌.
给水管网系统理论与分析[M]. 北京: 中国建筑工业出版社, 2003 : 154 -165.
ZHAO Hongbin. Water network system theories and analysis[M]. Beijing: China Architecture & Building Press, 2003 : 154 -165. |
| [14] |
常魁.虚拟现实技术在城市供水管网运行调度中的应用[D].哈尔滨:哈尔滨工业大学, 2008:55-69.
CHANG Kui. Application of virtual reality in urban water network operation scheduling[D]. Harbin: Harbin Institute of Technology, 2008:55-69. |
| [15] |
王国栋, 俞国平. 管段重要性指数在水力模型校核中的应用[J].
苏州科技学院学报(工程技术版), 2007, 20 (1) : 52-54.
WANG Guodong, YU Guoping. Application of significance index in hydraulic model calibration[J]. Jouranl of University of Science and Technology of Suzhou (Engineering and Technology), 2007, 20 (1) : 52-54. |
| [16] |
陶建科, 刘遂庆. 建立给水管网微观动态水力模型标准方法研究[J].
给水排水, 2000, 26 (5) : 4-8.
TAO Jianke, LIU Suiqing. Standard method research on micro-dynamic hydraulic model for water supply network[J]. Water & Wastewater Engineering, 2000, 26 (5) : 4-8. |
 2017, Vol. 49
2017, Vol. 49


