随着全球能源紧缺问题的日益加剧, 如何有效地降低建筑用能成为建筑领域内研究的重要问题.将相变材料应用于建筑围护结构中能够显著提高建筑的蓄热能力[1].在材料的凝固与融化过程中, 通过热量的吸收与释放能够降低室内空气温度波动, 有效防止室内过热[2], 进而有效减少空调能耗.因此, 利用相变材料进行潜热储能的方法能够同时满足建筑节能及提高室内舒适度的要求[3].近几十年来, 研究者对相变材料在建筑中的应用进行了诸多研究, 同时对相变墙体或相变储能系统的热工设计问题进行了相关探讨.袁艳平等[4]对脂肪酸类相变材料进行了大量研究, 同时对适用于相变储能系统的相变材料进行了实验分析, 将相变材料的热稳定性及相变储能系统中材料的传热特性进行了总结[5].Morshed Alam等[6]用EnergyPlus软件对澳大利亚8个城市应用5种不同相变材料的房间进行了能耗模拟, 结果显示,相变材料应用的有效性有赖于当地气象条件、室内温度设置、相变层厚度及表面积, 不同的相变材料在一年中的不同时间发挥作用.同时得出, 当相变温度处于室内设计温度之外时, 其节能潜力会下降. Takeda等[7]提出一种相变储能通风系统, 并对该系统在日本8个城市的应用效果进行了模拟, 结果表明,不同的环境条件会对系统的应用效果产生较大影响.可见, 相变材料在建筑中的应用受室外环境条件及室内设定条件的影响, 相变墙体或相变储能系统的优化需要将环境因素考虑在内.现今对相变材料应用效果的评价多是以温度及耗电量作为比较的依据, 并未反映出墙体或系统本身的热特性.因此, 有必要提出一种能够反映相变墙体或相变储能系统在不同环境条件下热工性能的设计参数.
在工程应用中, 往往用导热系数作为比较基准进行墙体材料的比选, 这对于普通材料尚可, 但对于相变材料, 由于相变潜热会在墙体传热过程中发挥很大作用, 且包括导热系数、比热等热物性参数会在相变过程中发生变化, 同时, 潜热的影响会随边界条件的变化而变化, 仅用导热系数难以将相变作用的影响计入在内去衡量相变墙体的传热特性, 从而难以根据单一参数对应用于墙体的相变材料进行评价与比较, 这造成了相变材料在工程应用上的困难.为此, 本文定义了能够反映复合墙体中相变层在相变应用周期内, 一定环境条件下传热特性的热物性参数--相对导热系数, 并利用该参数进行以下分析:在北京地区应用相变材料层后, 相变层全年的传热特性变化; 不同朝向墙体应用相变层后, 相变层传热特性变化的对比; 不同相变层应用于北京地区的比较与优选; 相变材料在中国不同地区建筑中应用效果的对比.
1 相对导热系数定对于单一材质的均质各项同性, 厚度为δ、面积为F、导热系数为λs的普通材料, 在一维稳态传热条件下, 其导热热流量为qs, 两侧表面温差为Δt.现有单一材质的相变材料, 其尺寸及两侧边界条件与普通材料完全相同, 在稳态传热条件下, 其导热热流量为qc.若将此相变材料视为普通材料, 将相变作用的影响考虑在内, 由傅里叶定律可得到其导热系数λc,即
| $\frac{{{\lambda _{\rm{c}}}}}{{{q_{\rm{c}}}}} = {\lambda _{\rm{s}}}{q_{\rm{s}}} = \frac{\delta }{{F\Delta t}},$ | (1) |
| ${\lambda _{\rm{c}}} = {\lambda _{\rm{s}}}\frac{{{q_{\rm{c}}}}}{{{q_{\rm{s}}}}}.$ | (2) |
即此时相变材料的导热系数相当于普通材料导热系数的qc/qs倍, 将此称为相变材料在该稳态传热条件下的相对导热系数.在一定环境条件下与定物性材料导热能力相同的导热系数定义为相变应用周期内相变材料的相对导热系数.
对于非稳态传热, 由于相变过程中的潜热会随温度变化, 相变潜热在传热过程中的作用会受边界条件的影响.此外, 相变材料在相变过程中导热系数及比热均会随温度发生变化.提出一种物性参数去评价相变材料或相变层在非稳态传热过程中的传热特性就变得极为困难.
现将相对导热系数应用于多层复合相变墙体的非稳态传热过程.假定相变复合墙体由n+1个材料层构成, 除相变层外其他各层的厚度及导热系数分别为δi及λi.同时有内部构成及尺寸与相变墙体相同的普通复合墙体, 只是将相变层替换为物性参数已知且保持不变的标准材料层, 在非稳态传热条件下, 相变材料应用周期的初始时刻为τi, 终了时刻为τe, 由综合温度为tout的室外空气经由普通墙体向温度为tin恒定不变的室内空气传递的热量为Qs, 而经由相变墙体的传热量为Qc.室内及室外空气与墙体表面的对流换热系数分别为hin、hout.规定相变层的相对导热系数由下式得到:
| $\frac{{{Q_{\rm{s}}}}}{{{Q_{\rm{c}}}}} = \frac{{\frac{1}{{{h_{{\rm{out}}}}}} + \frac{1}{{{h_{{\rm{in}}}}}} + \sum\limits_{i = 1}^n {\frac{{{\delta _i}}}{{{\lambda _i}}}} + \frac{\delta }{{{\lambda _{\rm{c}}}}}}}{{\frac{1}{{{h_{{\rm{out}}}}}} + \frac{1}{{{h_{{\rm{in}}}}}} + \sum\limits_{i = 1}^n {\frac{{{\delta _i}}}{{{\lambda _i}}}} + \frac{\delta }{{{\lambda _{\rm{s}}}}}}}.$ | (3) |
式中Qs及Qc可通过数值方法以实际环境条件为边界条件计算得到.热量计算是基于非稳态导热微分方程, 墙体传热过程中热阻、热容及相变潜热的影响均考虑在内.由于两种墙体除相变层或标准层外其他材料层均相同, 相变层或标准层热性能的差异就通过Qs与Qc的差异体现出来.由于λs可以给定, 通过式(3)即可计算得到λc.相变层或标准层热性能的差异便可通过λs与λc的比较反映出来.可以看出, 相对导热系数是一种能够反映热阻、热容及相变作用的综合热性能参数.相对导热系数越大, 说明由室外经过相变墙体向室内传递的热量越多, 相变层的传热能力越强.Qs及λs的给定提供了一种比较基准, 使得不同相变材料的传热性能得以比较.
相变层在非稳态传热过程中, 当相变层内部温度均低于或高于相变温度时, 相变材料未相变或完全相变, 传热过程仅受材料热阻及热容的影响, 相对导热系数的大小取决于材料本身导热系数及比热的大小.当相变层内部温度处于相变温度区间时, 部分相变材料会发生相变, 传热过程除受材料热阻及热容的影响外, 相变作用也会对传热过程产生影响, 相变区域越大, 影响越显著, 此时, 相对导热系数的大小不仅取决于材料热阻及热容, 还取决于相变潜热, 因此, 相变温度及潜热均是相对导热系数或者说相变层传热过程的重要影响因素.当室外环境在一天中的变化较剧烈(过渡季节)或不同天环境差异较大(晴天转阴天), 而相变层内部温度又恰好处于相变温度区间时, 由于相变潜热的存在显著提高了相变层的蓄热能力, 相变作用或者说相变层的蓄热能力将对传热过程产生重要影响, 表现在室外空气综合温度较高时室内的热量显著降低, 室外空气综合温度较低时室内失热量同样会降低, 同时, 相变层的相对导热系数值明显较小.
墙体中相变层的相对导热系数为
| ${\lambda _{\rm{c}}} = \frac{1}{{A\frac{{{Q_{\rm{s}}}}}{{{Q_{\rm{c}}}}} + B}},$ | (4) |
| $A = \frac{1}{\delta }\left( {\frac{1}{{{h_{{\rm{out}}}}}} + \frac{1}{{{h_{{\rm{in}}}}}} + \sum\limits_{i = 1}^n {\frac{{{\delta _i}}}{{{\lambda _i}}}} + \frac{1}{{{\lambda _{\rm{s}}}}}} \right),$ | (5) |
| $B = - \frac{1}{\delta }\left( {\frac{1}{{{h_{{\rm{out}}}}}} + \frac{1}{{{h_{{\rm{in}}}}}} + \sum\limits_{i = 1}^n {\frac{{{\delta _i}}}{{{\lambda _i}}}} } \right).$ | (6) |
式中A、B为常数项.可以看出, 相变层相对导热系数的大小与墙体边界条件、相变层厚度及位置有关, 并非定值, 反映的是该相变层在某种条件下的热传递特性.通过相对导热系数将相变作用的影响考虑在内, 对相变层的传热特性进行折算, 使得不同相变层之间具有可比性, 可用其进行不同环境条件下不同相变材料层应用效果的研究.
2 数学模墙体的构造及其边界的换热情况如图 1所示.墙体由室外侧至室内侧分别由保温层、普通砖层、标准层或相变层构成.墙体外表面换热包括辐射换热及对流换热, 墙体内表面仅有对流换热而忽略辐射换热.假设室内空气温度维持恒定, 即室内全年维持空调工况.
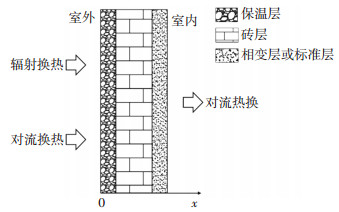
|
图 1 墙体构造及边界的换热情况 Figure 1 Wall structure and boundary condition |
由于相变材料的传热问题为非线性问题, 可用焓法进行求解.墙体传热的控制方程为
| $\rho \frac{{\partial H}}{{\partial \tau }} = \lambda \frac{{{\partial ^2}t}}{{\partial {x^2}}}.$ | (7) |
其中, 对于相变材料层:
固相区
| $H = \int_{{t_0}}^{{t_1}} {{c_{{\rm{p,s}}}}} {\rm{d}}t.$ | (8) |
两相区
| $H = \int_{{t_0}}^{{t_{{\rm{solid}}}}} {{c_{{\rm{p,s}}}}} {\rm{d}}t + \int_{{t_{{\rm{solid}}}}}^{{t_1}} {{c_{{\rm{p,m}}}}{\rm{d}}t} .$ | (9) |
液相区
| $H = \int_{{t_0}}^{{t_{{\rm{solid}}}}} {{c_{{\rm{p,s}}}}{\rm{d}}t} + \int_{{t_{{\rm{solid}}}}}^{{t_{{\rm{liquid}}}}} {{c_{{\rm{p,m}}}}{\rm{d}}t} + \int_{{t_{{\rm{liquid}}}}}^{{t_1}} {{c_{{\rm{p,l}}}}{\rm{d}}t} .$ | (10) |
对于标准材料层
| $H = \int_{_{{t_0}}}^{^{{t_1}}} {{c_{\rm{p}}}{\rm{d}}t.} $ | (11) |
式中:ρ为材料密度, kg/m3; H为材料焓值, J/kg; τ为时间, s; t为温度, ℃; x为墙体厚度方向, 即热流传递方向坐标, 以墙体外表面为坐标原点, m; cp为材料比热, J/(kg·℃); cp, s、cp, l分别为相变材料固相及液相的比热, cp, m为两相区的等效比热, 以相变区的潜热等效均分.
初始条件为
| $t\left( {x,\tau } \right)\left| {_{\tau = 0}} \right. = {t_{{\rm{init}}}}.$ | (12) |
墙体外边界条件为
| ${q_{{\rm{r}},{\rm{out}}}} + {h_{{\rm{out}}}}{t_{{\rm{out}}}} - {t_{{\rm{s}},{\rm{out}}}} = {\lambda _{{\rm{s}},{\rm{out}}}}\frac{{\partial t}}{{\partial x}}{{\rm{|}}_{x = 0}}.$ | (13) |
墙体内边界条件为
| ${h_{{\rm{int}}}}\left( {{t_{{\rm{in}}}} - {t_{{\rm{s}},{\rm{in}}}}} \right) = {\lambda _{{\rm{s}},{\rm{in}}}}\frac{{\partial t}}{{\partial x}}{|_{x = \delta }}.$ | (14) |
式中, tinit为计算月初始温度, ℃; qr, out为室外环境对墙体的辐射热流, W; hout为室外空气与墙体外表面的对流换热系数, W/(m2·℃); tout为室外空气温度, ℃; ts, out为墙体外表面温度, ℃; λs, out为墙体外表面材料的导热系数, W/(m·℃); hin为室内空气与墙体内表面的对流换热系数, W/(m2·℃); tin为室内空气温度, ℃; ts, in为墙体内表面温度, ℃; λs, in为墙体内表面材料的导热系数, W/(m·℃); δ为墙体总厚度, m.
模拟过程的基本假设如下[8]:
墙体传热为一维非稳态传热; 除相变材料外, 墙体材料均为均质各向同性材料; 墙体表面与空气的对流换热系数维持恒定; 墙体表面各点所接受的辐射热量相同.
3 房间模型及条件设模拟房间尺寸为5 m×5 m×3 m, 房间四面均为外墙, 为便于分析比较, 仅在一面外墙设置相变层, 相变层厚度为3 cm.保温层及砖层厚度分别为4、30 cm.墙体外表面与空气的对流换热系数为18.6 W/(m2·℃), 墙体内表面与空气的对流换热系数为8.7 W/(m2·℃) [9].假定室内全年维持在空调工况25 ℃.
标准层为密度1 000 kg/m3、比热1 000 J/(kg·℃)、导热系数0.5 W/(m·℃)的纯石膏板[10].相变层由相变材料及建筑材料复合而成[11-15], 材料层及保温层、砖层的物性参数如表 1所示.为便于对相变层在全年中的应用效果进行比较分析, 以1个月作为1个相变应用周期即比较周期.为使相变层在各月具有可比性, 在每个计算月的初始时刻, 其计算条件应与相同环境条件下标准层的初始条件完全相同, 并保证相变层与标准层的尺寸与边界条件完全相同.
| 表 1 墙体各层物性参数 Table 1 Thermo-physical parameters of wall layers |
为比较不同相变材料的应用效果, 选取了5种具有不同热物性参数的相变层, 见表 1.为比较相变材料在不同地区的应用效果, 选取了沈阳、北京、南京、上海、广州5个城市的气象数据作为建筑的室外计算条件.其中沈阳为严寒地区, 北京为寒冷地区, 南京、上海为夏热冬冷地区、广州为夏热冬暖地区.气象数据为中国气象局气象台站的实测数据, 取各地区典型气象年的逐时数据进行分析.各城市全年室外空气月平均温度及月平均日总太阳辐照量的变化如图 2、3所示.
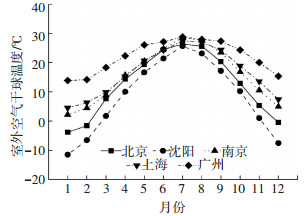
|
图 2 各地全年室外空气月平均温度 Figure 2 Outdoor air monthly mean temperature in different area |
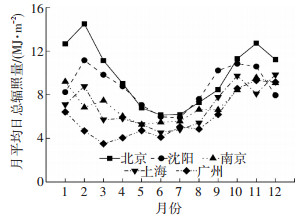
|
图 3 各地全年月平均日总太阳辐照量 Figure 3 Monthly mean sunlight radiation in different area |
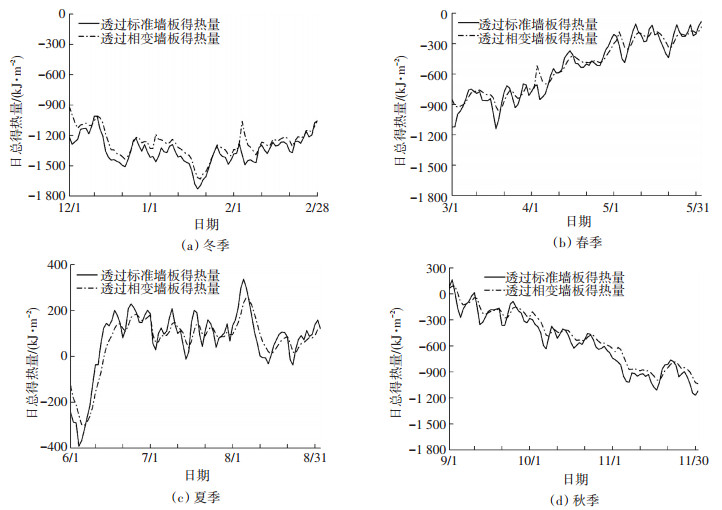
在北京地区建筑南墙分别应用标准层及相变层Ⅰ后, 墙体内表面热流全年变化如图 4所示.图 4(a)、(b)、(c)、(d)分别为冬季、春季、夏季、秋季的变化.可以看出, 夏季6、7、8月透过墙体的热流为正值, 即建筑存在冷负荷, 其他月份均为负值, 即存在热负荷.
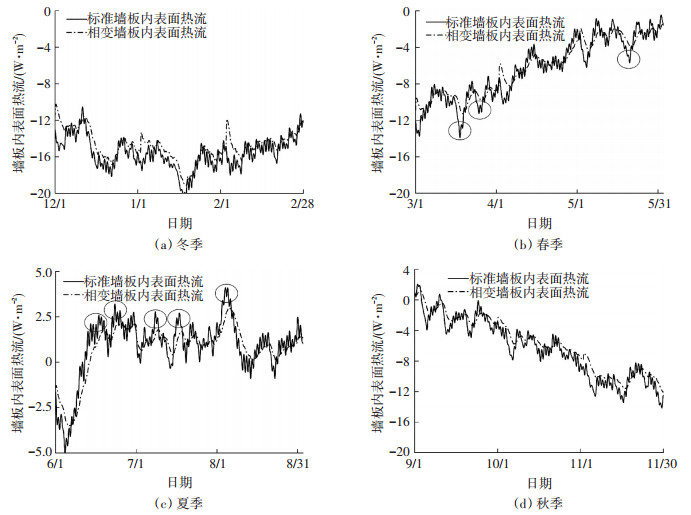
|
图 4 墙体内表面热流变化 Figure 4 Heat flux on the internal surface of the wal |
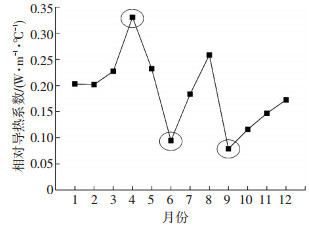
相变墙体内表面热流与标准墙体的热流呈现近似一致的变化趋势, 但相变墙体的变化更加平稳.这一方面是由于相变层本身的导热系数要小于标准层, 另一方面, 当室外温度在某几天相较于前几天有较大波动时, 相变层由于相变作用其蓄热能力大大增强, 从而削弱墙体表面的温度波动.在春、秋、冬季, 透过相变墙体的热流经常低于标准墙体, 尤其是在3、5月份, 室外温度出现较大波动时, 差异非常明显, 如图 4(b)中圆圈所示.在夏季, 由于每天的室外温度在相变温度附近波动, 从而使相变层在每天重复地蓄、放热, 相变潜热的影响增强, 体现为墙体热流在较高时能够削弱, 如图 4(c)中圆圈所示, 而在较低时能够增强.透过墙体内表面的日总得热量全年变化如图 5所示.其变化与热流变化情况相同, 除夏季6、7、8月得热量为正值外, 其他月份均为负值, 即建筑失热.根据标准墙体及相变墙体各月的总得热量及式(4)即可得出相变层相对导热系数的全年变化规律, 如图 6所示.可以看出, 尽管相变层的导热系数为0.23 W/(m·℃), 但相对导热系数与其有较大差异, 且在全年有较大变化, 大体在0.07~0.33 W/(m·℃)内波动, 在4月份出现最高值, 为0.33 W/(m·℃), 相变层传热能力有所增强, 在此期间, 相变层的传热能力相当于导热系数为0.33 W/(m·℃)的标准层的传热能力.相对导热系数在6、9月份出现最低值, 低于0.1 W/(m·℃), 如图中圆圈所示, 相变层的传热能力大大降低, 可能是由于6、9月份恰好是冷、暖过渡月份, 相变层内部温度处于相变区间附近, 相变潜热的作用有所增强, 温度的波动能够在很大程度上被削减, 墙体内表面温度与室内温度的差异性较小, 从而使墙体的吸热量及放热量均有所减小.
|
图 5 透过墙体内表面建筑日总得热量变化 Figure 5 Heat gained through the internal surface of the wal |
|
图 6 相变层相对导热系数变化 Figure 6 Changes of PCM layers RT |
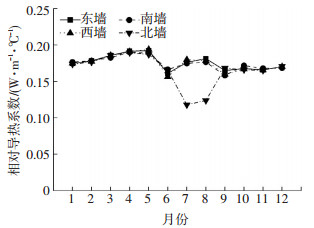
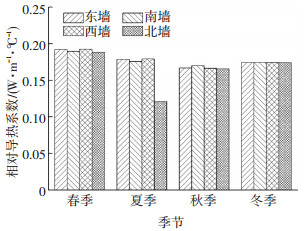
在北京地区的同一建筑中将相变层Ⅲ分别应用于东墙、南墙、西墙、北墙后, 相变层的相对导热系数全年变化如图 7所示.除北墙的相对导热系数在7、8月份较低外, 其他朝向墙体在全年的变化不大, 且各墙体变化较一致, 均在0.1~0.2 W/(m·℃)内变化.东向、南向、西向墙体在6、9月份均出现低谷值, 约为0.15 W/(m·℃), 而北向墙体出现在7、8月份, 为0.12 W/(m·℃).各朝向相变层相对导热系数的季节性变化如图 8所示.各季节的相对导热系数值均为季节内3个月相对导热系数的平均值.可以看出, 除北墙外, 其他墙体的季节性变化并不明显.可以说, 对于东向、南向、西向墙体, 在各个季节的应用效果并没有太大变化, 而对于北向墙体, 在夏季的传热特性与其他季节有显著不同, 夏季相变层的相变作用增强, 从而其蓄热能力增强, 导致其传热能力明显降低.
|
图 7 各朝向相对导热系数全年变化 Figure 7 Monthly changes of RTC in different orientation |
|
图 8 各朝向相对导热系数季节变化 Figure 8 Seasonal changes of RTC in different orientation |
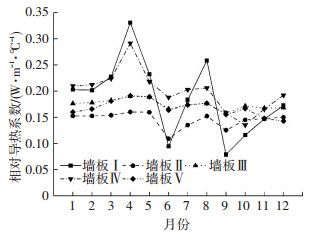
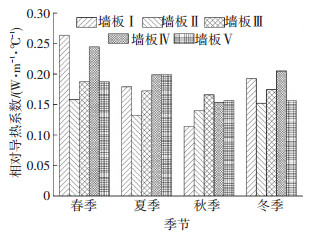
在北京地区, 分别将5种相变层应用于建筑南墙后, 相变层相对导热系数全年变化如图 9所示.不同物性参数的相变层在同一地区的传热特性变化有较为明显的不同.相变层Ⅰ与Ⅳ的变化最剧烈, Ⅰ相对导热系数的最大值与最小值的差为0.25 W/(m·℃), Ⅳ的差值为0.15 W/(m·℃), 且均在4月出现最大值, 相变层Ⅰ在6、9月份出现低谷值, 9月份的相对导热系数为全年最低值, Ⅳ在6、10月份出现低谷值, 10月份的相对导热系数为全年最低值.Ⅱ的相对导热系数除在6、9月份出现低谷值外, 其他月份均维持在0.15 W/(m·℃)附近, 变化很小, 最大值与最小值的差为0.05 W/(m·℃).Ⅲ的变化情况已在4.2.1中详述.相变层Ⅴ的变化与Ⅲ相似, 相比于其他相变层, 两者传热特性的变化均较稳定.5种相变层的季节性变化如图 10所示.Ⅰ与Ⅳ的季节性变化最明显, Ⅰ与Ⅳ在春季及冬季的相对导热系数相比其他相变层明显较高, 但Ⅰ在秋季的值明显较低.Ⅱ的值在各个季节均较低, Ⅲ与Ⅴ在全年的变化不大.因此, Ⅰ及Ⅳ在冬季及春季的传热能力较强, 从降低空调能耗的角度考虑, 其应用存在显著不足.Ⅲ与Ⅴ的传热能力在各个季节均较稳定, 考虑到全年性应用, Ⅱ在各个季节的相对导热系数均能维持在较低水平, 应用于北京最合适.可以看出, 由于相对导热系数能够反映相变层的传热特性, 不同相变层的相对导热系数能够为材料层的比较提供参考, 从而为相变材料的优选进行有效指导.
|
图 9 不同墙体相对导热系数全年变化 Figure 9 Monthly changes of different PCM wallboards RT |
|
图 10 不同墙体相对导热系数季节变化 Figure 10 Seasonal changes of different PCM wallboards RT |
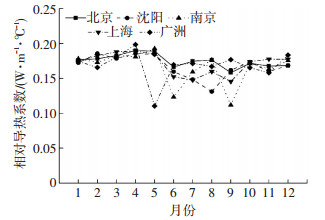
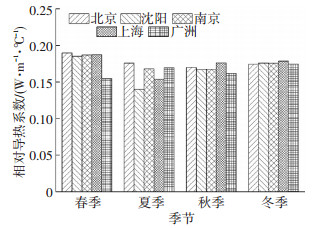
分别在北京、沈阳、南京、上海、广州将相变层Ⅲ应用于建筑南墙后, 相变层相对导热系数全年变化如图 11所示.由图 2、3可以看出, 各城市全年室外空气月平均温度及月平均日总太阳辐照量均有差异, 因此, 相同的相变层在不同地区的传热特性变化有较明显的不同.北京地区的变化情况已在4.2.1及4.2.2中详述.对于沈阳地区, 由于冷、热负荷交替集中出现在8月, 在该月出现了谷值, 最高与最低值相差0.06 W/(m·℃).南京在6、9月出现了谷值, 最高与最低值相差0.08 W/(m·℃).上海地区6~9月份的值均较低, 而其他月份稍高, 最高与最低值相差0.04 W/(m·℃).而对于广州地区, 冷、热负荷交替出现在5月, 此月份出现谷值, 最高与最低值相差0.09 W/(m·℃).5个城市相对导热系数的季节变化如图 12所示.可以看出, 将相变层Ⅲ应用在北京、南京、上海, 全年的传热特性变化不大, 且三者间差别不大, 而应用在沈阳, 夏季的热阻值明显较大, 应用在广州, 春季的热阻值明显较大, 在其他季节, 两者与其他3个城市差别不大.因此, 由于气候的差异性, 即使是同一相变材料层, 在不同地区的应用情况仍会有显著不同.若应用在沈阳, 考虑到降低空调能耗, 夏季的应用效果要明显优于其他城市, 若应用在广州, 春季的应用效果要明显优于其他城市.由以上分析可得, 利用相对导热系数能够直观地反映相变层全年的动态传热特性, 从而对相变材料的应用效果进行有效评估.
|
图 11 不同地区相对导热系数全年变化 Figure 11 Monthly changes of RTC in different area |
|
图 12 不同地区相对导热系数季节变化 Figure 12 Seasonal changes of RTC in different area |
1)考虑到相变材料在传热过程中比热、导热系数等参数的变化及相变潜热对传热过程的影响, 本文提出相对导热系数用以表征在这种综合作用下相变层的传热能力.在一定环境条件下与定物性材料导热能力相同的导热系数定义为相变应用周期内相变材料的相对导热系数.
2)相对导热系数能够直观地反映相变层全年的动态传热特性, 从而对相变材料的应用效果进行有效评估.通过分析相变层Ⅰ在北京地区建筑南墙的相对导热系数,得出相变层的应用效果在全年有较大变化, 4月份相对导热系数出现最高值(0.33 W·m-1·℃-1), 墙体传热能力增强, 6、9月份出现低值( < 0.1 W·m-1·℃-1), 墙体传热能力大大降低.相变层在不同朝向的应用效果会有较大差异.通过对相变层Ⅲ在5个城市的相对导热系数进行分析可以看出, 考虑到减少空调能耗, 相变层若应用在沈阳, 夏季的应用效果要明显优于其他城市, 若应用在广州, 春季的应用效果要明显优于其他城市.
3)由于相对导热系数能够反映相变层的传热特性, 不同相变层的相对导热系数值能够为材料层的比较提供参考, 从而为相变材料的优选进行有效指导.通过对5种相变层的相对导热系数进行对比,得出Ⅰ及Ⅳ在冬季及春季的传热能力较强, 从减少空调能耗的角度考虑, 其应用存在显著不足, Ⅲ与Ⅴ的传热能力在各个季节均较稳定, 考虑到全年性应用, Ⅱ在各个季节的相对导热系数均能维持在较低水平, 应用于北京最合适.
| [1] | MEMON S A. Phase change materials integrated in building walls: A state of the art review[J]. Renewable and Sustainable Energy Reviews, 2014, 31 (31) : 870-906. |
| [2] | OSTERMAN E, TYAGI VV, BUTALA V, et al. Review of PCM based cooling technologies for buildings[J]. Energy and Buildings, 2012, 49 (2) : 37-49. |
| [3] | ZHOU D, ZHAO C Y, TIAN Y. Review on thermal energy storage with phase change materials (PCMs) in building applications[J]. Applied Energy, 2012, 92 (4) : 593-605. |
| [4] | ZHANG Nan, YUAN Yanping, DU Yanxia, et al. Preparation and properties of palmitic-stearic acid eutectic mixture/expanded graphite composite as phase change material for energy storage[J]. Energy, 2014, 78 : 950-956. DOI: 10.1016/j.energy.2014.10.092 |
| [5] | YUAN Yanping, ZHANG Nan, TAO Wenquan, et al. Fatty acids as phase change materials: A review[J]. Renewable and Sustainable Energy Reviews, 2014, 29 (7) : 482-498. |
| [6] | ALAM M, JAMIL H, SANJAYAN J, et al. Energy saving potential of phase change materials in major Australian cities[J]. Energy and Buildings, 2014, 78 (4) : 192-201. |
| [7] | TAKEDA S, NAGANO K, MOCHIDA T, et al. Development of a ventilation system utilizing thermal energy storage for granules containing phase change material[J]. Solar Energy, 2004, 77 (3) : 329-338. DOI: 10.1016/j.solener.2004.04.014 |
| [8] | ZHOU Guobing, ZHANG Yinping, LIN Kunping, et al. Thermal analysis of a direct-gain room with shape-stabilized PCM plates[J]. Renewable Energy, 2008, 33 (6) : 1228-1236. DOI: 10.1016/j.renene.2007.06.024 |
| [9] | ZHANG Yinping, LIN Kunping, JIANG Yi, et al. Thermal storage and nonlinear heat-transfer characteristics of PCM wallboard[J]. Energy and Buildings, 2008, 40 (9) : 1771-1779. DOI: 10.1016/j.enbuild.2008.03.005 |
| [10] | YAHAY N A, AHMAD H. Numerical investigation of indoor air temperature with the application of PCM gypsum board as ceiling panels in buildings[J]. Procedia Engineering, 2011, 20 : 238-248. DOI: 10.1016/j.proeng.2011.11.161 |
| [11] | ZHOU T, DARKWA J, KOKOGIANNAKIS G. Thermal evaluation of laminated composite phase change material gypsum board under dynamic conditions[J]. Renewable Energy, 2015, 78 : 448-456. DOI: 10.1016/j.renene.2015.01.025 |
| [12] | ZWANZIG S D, LIAN Y, BREHOB E G. Numerical simulation of phase change material composite wallboard in a multi-layered building envelope[J]. Energy Conversion and Management, 2013, 69 (3) : 27-40. |
| [13] | CASTELL A, FARID M M. Experimental validation of a methodology to assess PCM effectiveness in cooling building envelopes passively[J]. Energy and Buildings, 2014, 81 : 59-71. DOI: 10.1016/j.enbuild.2014.06.011 |
| [14] | TABARES-VELASCO P C, CHRISTENSEN C, BIANCHI M. Verification and validation of energy plus phase change material model for opaque wall assemblies[J]. Building and Environment, 2012, 54 (7) : 186-196. |
| [15] | TARDIEU A, BEHZADI S, CHEN J J, et al. Computer simulation and experimental measurements for an experimental PCM-impregnated office building [C] // Proceedings of Building Simulation 2011: 12th Conference of International Building Performance Simulation Association. Sydney, 2011:56-63. |
 2017, Vol. 49
2017, Vol. 49


