2. 中国科学院水利部成都山地灾害与环境研究所,成都610041;
3. 中国科学院大学,北京100049
2. Institute of Mountain Hazards and Environment, Chinese Academy of Sciences & Ministry of Water Resources, Chengdu 610041, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
泥石流是我国最主要的地质灾害之一,修建在泥石流高发区的铁路和公路桥梁,在建设运营过程中都面临艰巨的泥石流防治任务[1-2].泥石流对桥梁的危害方式主要包括冲击、冲刷和淤埋,尤以大块石对桥梁的冲击力最为显著[3-4].实践表明,许多桥梁被泥石流毁坏多与泥石流大块石对桥墩的冲击破坏有关[5].因此,有关泥石流大块石的冲击力计算成为泥石流灾害防治研究的热点.目前,国内外计算泥石流大块石冲击力的主要方法较多.如章书成[6]以结构力学为基础,将柱型构筑物简化为悬臂梁、简支梁模型来计算泥石流大块石作用于梳子坝支墩、桥梁等柱型结构上的冲击力.工程实践表明,此法计算结果比估计的承载力大[7].Thornton[8]视泥石流块石与构筑物分别为刚性体和塑性体来计算泥石流块石对构筑物的冲击力,其适用于强度较低的构筑物被冲击的情况[3].Yamaguchi[9]、Mizuyama[10]、Braccesi等[11]和黄宏斌等[12]以Hertz弹性碰撞理论为基础,采用修正系数的方法来综合考虑系统材料、冲击过程中摩擦、断裂等因素对冲击力的综合影响.这种基于Hertz理论进行修正的方法是目前国内外计算泥石流大块石冲击力的主流方法之一.但其最大的不足是修正系数力学意义模糊,一般通过工程经验或实验确定,具有主观性强、成本高昂或耗时周期长等缺点.
本文针对泥石流中大块石对桥墩的冲击这一具体形式进行研究.以Hertz碰撞理论为基础,根据冲击系统中对象的材料特性、冲击物体的相对大小及结构变位对冲击力进行修正,其考虑因素全面,理论依据充分,参数明确,使用方便,可为泥石流多发区的桥梁设计及防护提供可信的计算方法.
1 Hertz碰撞理论Hertz在假设两球接触面半径为a的圆的前提下,给出了两个球体在压力P作用下的完备解,并给出了碰撞时的冲击力公式(1)、(2) (图 1)[13].
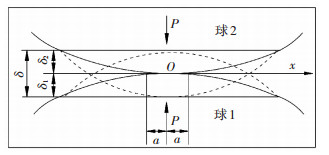
|
图 1 Hertz弹性碰撞模型 Figure 1 Elastic collision model of Hertz |
接触压力P(r)分布公式为
| $P\left( r \right) = \frac{{2E{R^{\frac{1}{2}}}{\delta ^{\frac{3}{2}}}}}{{{\rm{ \mathsf{ π} }}{a^2}}}{\left[ {1 - {{\left( {\frac{r}{a}} \right)}^2}} \right]^{\frac{1}{2}}}.$ | (1) |
式中:
两球碰撞时的冲击力
| $F = \frac{{4\sqrt R }}{{3{\rm{ \mathsf{ π} }}({k_1} + {k_2})}}{\delta ^{\frac{3}{2}}}.$ | (2) |
式中
根据牛顿第二定律,则有
| $\frac{{{{\rm{d}}^2}\delta }}{{{\rm{d}}{t^2}}} = \frac{{{{\rm{d}}^2}{\delta _1}}}{{{\rm{d}}{t^2}}} + \frac{{{{\rm{d}}^2}{\delta _2}}}{{{\rm{d}}{t^2}}} = (\frac{1}{{{m_1}}} + \frac{1}{{{m_2}}})\left( { - F} \right),$ | (3) |
由式(2)、(3)得
| $m\frac{{{{\rm{d}}^2}\delta }}{{{\rm{d}}{t^2}}} + \frac{{4\sqrt R }}{{3{\rm{ \mathsf{ π} }}({k_1} + {k_2})}}{\delta ^{\frac{3}{2}}} = 0.$ | (4) |
对式(4)进行积分,则弹性碰撞力
| ${F_{\rm{e}}} = {\left( {\frac{{5m{V^2}}}{4}} \right)^{\frac{3}{5}}}{\left( {\frac{{4\sqrt R }}{{3{\rm{ \mathsf{ π} }}({k_1} + {k_2})}}} \right)^{\frac{2}{5}}}.$ | (5) |
式中
桥墩截面形状一般为圆形、方形及其复合形状,墩底置于足够深度的位置,目前大多将其简化为悬臂梁结构和简支梁结构.实际上,桥墩结构不是纯粹的悬臂结构,更不是简支结构.工程实践中应合理地考虑上部桥梁对墩顶的约束作用.因而桥墩结构应为墩底为固定支座,墩顶为定向支座的一种复合约束结构.在块石冲击力作用下,由于桥梁与墩顶之间的摩擦力对墩顶的约束从而保证墩顶不发生位移时,按照桥墩两端为固定支座考虑;当冲击力足够大时,桥墩可往一个方向产生一定的位移,此时桥墩结构为墩底为固定支座、墩顶为定向支座外加恒定摩擦反力G·f作用的复合结构,其中G为桥梁上部结构作用在墩顶的重力,f为支座的动摩擦系数.
将大块石简化为均匀球体,以速度V撞击桥墩,撞击位置位于li处;桥墩截面为圆形,总长l.可以建立如图 2所示的泥石流大块石冲击计算模型.
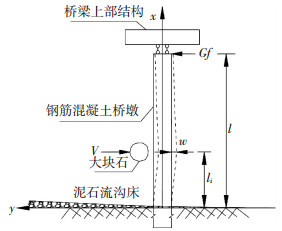
|
图 2 泥石流大块石冲击桥墩模型 Figure 2 Impact model of boulder on piers in debris flow |
目前基于Hertz碰撞理论的冲击力计算公式中,推导出的绝大多数冲击力公式是基于球体的应力应变关系为弹性碰撞这一假设条件得来,而实践中大多数工程材料为应力应变关系较复杂的弹塑性体,直接使用Hertz弹性碰撞的冲击力公式所计算出的结果必然偏大;大多数公式只考虑冲击物体的大小对冲击力的影响,事实上,被冲击物的大小也是影响冲击力大小的关键所在;物体碰撞过程中,被撞物体均有不同程度的变形,从能量守恒的观点来看,物体的被撞击位置不同,其变形程度也不同,从而相应的冲击力也一定不同.本文基于以上3个方面,量化冲击系统中对象的材料性质、相对尺寸大小及构筑物的结构变位对冲击力的影响,最终导出泥石流中大块石对桥梁冲击力大小的计算公式.
当被冲击物的半径R2和质量m2均趋于无穷大,即R2=∞,m2=∞时,由式(1)和(5)中等效质量和等效半径表达式可得R=R1,m=m1,由此导出冲击力计算公式为
| ${F_{\rm{e}}} = \left[ {\frac{4}{{3{\rm{ \mathsf{ π} }}{{({k_1} + {k_2})}^{0.4}}}}} \right]{\left( {\frac{{5\rho {{\rm{ \mathsf{ π} }}^2}}}{4}} \right)^{0.6}}{V^{1.2}} \times {R^2},$ | (6) |
式中ρ为冲击物体的密度.
式(6)仅适用于碰撞系统材料性质为弹性、被撞击物体尺寸为无穷大及忽略被撞击物结构变位的情况,因此,在工程实践中,直接应用式(6)计算出的冲击力势必会与实际值有较大差别.为此,引入相应的修正系数来考虑碰撞过程中系统对象的材料性质、相对尺寸大小和结构变位对冲击力的影响,则实际冲击力计算公式如下:
| $F = {k_{\rm{e}}}\left[ {\frac{4}{{3{\rm{ \mathsf{ π} }}{{({k_1} + {k_2})}^{0.4}}}}} \right]{\left( {\frac{{5\rho {{\rm{ \mathsf{ π} }}^2}}}{4}} \right)^{0.6}}{V^{0.8}} \times {R^2}.$ | (7) |
式中kc=kc1kc2kc3为综合修正系数,其中kc1,kc2,kc3分别为冲击系统的材料修正系数、球径比(R2/R1)修正系数和结构变位修正系数.
可以看出,式(6)与式(7)中冲击物速度的幂次方不同,这主要是本文将名义材料修正系数中的速度分项合并到冲击力计算公式,方便单独量化材料性质对冲击力的影响所致,具体见修正系数kc1,kc2,kc3的推导过程.
3.1 材料修正系数kc1国内外学者发现,基于Hertz接触力学所提出的冲击力计算公式中,其计算结果往往比实际观测结果大1~2个数量级[14],这是由于实际工程材料与Hertz接触力学假定的弹性材料在力学效应上存在显著区别.何思明等以Hertz碰撞理论、Thornton接触力学模型和牛顿第二定律,推导出被撞结构为无穷大时的最大压缩量和冲击力计算公式[15]为
| ${\delta _{{\rm{max}}}} = {\left[ {\frac{{15m{{(V\cos \theta )}^2}}}{{16{R^{\frac{1}{2}}}E}}} \right]^{\frac{2}{5}}}.$ | (8) |
| ${F_{{\rm{ep}}}} = \frac{4}{3}E{R^{\frac{1}{2}}}\delta _{\max }^{\frac{3}{2}} - 2{\rm{ \mathsf{ π} }}\int_0^{{a_{\rm{p}}}} {\left[ {P\left( r \right) - {P_y}} \right]} rdr.$ | (9) |
式中:θ为冲击角度,ap为构筑物塑性区半径,Py为接触屈服压应力.
可以看出,基于Hertz接触力学推导的冲击力计算公式(6)和(9)仅在碰撞系统的材料上有区别.因此,可根据式(6)、(9)推导出材料修正系数kc1.
根据Hertz接触力学理论和Thornton接触力学模型,存在如式(10)、(11)[16]的关系:
| $R\delta = a_{\rm{p}}^2 + a_{\rm{y}}^2 = {a^2},$ | (10) |
| ${\rm{ \mathsf{ π} }}R{P_{\rm{y}}} = 2E{a_{\rm{y}}}.$ | (11) |
式中ay为初始屈服对应的接触面半径.
假设冲击过程中被冲击构筑物材料满足Mises屈服准则[17],则初始屈服应力服从式(12)的关系:
| ${P_{\rm{y}}} = \left( {1.234 + 1.256\mu } \right)Y.$ | (12) |
式中Y为接触材料的屈服强度.
综合式(1)、(8)~(12),可推导出考虑冲击作用为正碰,被冲击结构材料为弹塑性材料时的冲击力公式:
| ${F_{{\rm{ep}}}} = \frac{4}{3}E{R^{\frac{1}{2}}}{\left( {\frac{{15m{V^2}}}{{16{R^{\frac{1}{2}}}E}}} \right)^{\frac{3}{5}}}{\left( {\frac{{{a_{\rm{y}}}}}{a}} \right)^3} + {\rm{ \mathsf{ π} }}{P_{\rm{y}}}a_{\rm{p}}^2.$ | (13) |
文献[15]的研究结果表明,块石与混凝土组成的冲击系统的临塑冲击速度很小,实践中泥石流速度一般都会超过临界速度,其势必在接触面上形成大范围的塑性变形区,此时材料初始屈服半径较塑性区半径至少小一个数量级,因此,名义材料修正系数为
| $k_{{\rm{c1}}}^* = \frac{{{F_{{\rm{ep}}}}}}{{{F_{\rm{e}}}}} = \frac{{3{\rm{ \mathsf{ π} }}\left( {1.234 + 1.256\mu } \right)Y}}{{{{(1{\rm{ }}280{\rm{ \mathsf{ π} }}{E^4})}^{0.2}}}}{V^{ - 0.4}}.$ | (14) |
实际材料修正系数只考虑材料对冲击力的影响,因此,将名义材料修正系数中的速度分项合并到式(6)中的速度分项,得出实际冲击力计算式(7)中最终的材料修正系数为
| ${k_{{\rm{c}}1}} = \frac{{3{\rm{ \mathsf{ π} }}\left( {1.234 + 1.256\mu } \right)Y}}{{{{(1{\rm{ }}280{\rm{ \mathsf{ π} }}{E^4})}^{0.2}}}}.$ | (15) |
由上述可知,冲击系统最大压缩量、塑性区半径与等效半径R分别呈反相关、正相关关系,而等效半径R随被冲击物半径的增长而增加,进而表明了冲击力大小与被冲击物尺寸大小有关.
为量化被冲击物尺寸对冲击力的影响,定义球径比为n1=R2/R1,其中R1、R2是冲击物和被冲击物的代表半径.以被冲击物代表半径为无穷大作基准,则根据式(5),可求出不同球径比下冲击力与被冲击物为半无限空间体时冲击力的比值Fen/Fe∞,其中Fen和Fe∞分别为不同球径比下的冲击力和被撞结构代表半径为无穷大的冲击力.则球径比修正系数kc2最终表达式如下:
| ${k_{{\rm{c}}2}} = \frac{{{F_{{\rm{en}}}}}}{{{F_{{\rm{e}}\infty }}}} = \frac{{n_1^2}}{{{{(1 + n_1^3)}^{0.6}}{{(1 + {n_1})}^{0.2}}}}.$ | (16) |
混凝土桥墩在不同大块石冲击力作用下,墩顶将会出现不同的变形响应.当冲击力在墩顶产生的附加力小于桥梁上部结构与墩顶的最大摩擦力时,墩顶将保持不动,此时桥梁结构视为两端固定的力学模型;当冲击力足够大时,墩顶产生一定量沿冲击方向的位移时,桥梁结构视为墩底为固定支座、墩顶为定向支座附加恒定动摩擦力的力学模型.
根据机械能守恒定律,冲击过程中将动能转化成桥墩的应变能,则由结构力学可推导出桥墩应变能公式:
墩顶无位移时
| ${V_{\varepsilon 1}} = \frac{{{F_i}^2l_i^3{{(l - {l_i})}^3}}}{{6EI{l^3}}}.$ | (17) |
墩顶有位移时,令Gf=n2F,考虑到上部桥梁的自重、支座设计摩擦系数及大块石冲击荷载,一般情况下n2≤0.2[18],则有
| ${V_{\varepsilon 2}} = \frac{{{F_i}^2\left( {4{n^2}_2{l^4} - 15{n_2}{l^2}_i{l^2} + 4{l^3}_il(1 + {n_2}) + 3{l^4}_i} \right)}}{{24EIl}}.$ | (18) |
冲击过程中,冲击在离固定端越近的位置其相应的冲击力越大.泥石流冲击桥墩时,其离墩底最近的冲击位置为R处,以此位置冲击力为基准,令冲击力结构变位修正系数kc3=Fi/FR,则有:
墩顶无位移时
| ${k_{{\rm{c}}3}} = {\left( {\frac{{{R^3}{{\left( {l - R} \right)}^3}}}{{l_i^3{{(l - {l_i})}^3}}}} \right)^{\frac{1}{2}}}.$ | (19) |
墩顶有位移时
| ${k_{{\rm{c}}3}} = {\left( {\frac{{4n_2^2{l^4} - 15{n_2}{R^2}{l^2} + 4{R^3}l(1 + {n_2}) + 3{R^4}}}{{4n_2^2{l^4} - 15{n_2}l_i^2{l^2} + 4l_i^3l(1 + {n_2}) + 3l_i^4}}} \right)^{\frac{1}{2}}}.$ | (20) |
冲击修正系数kc3表达式的选择,需先经试算后再确定.首先假设在墩顶无位移的情况下求得相应的冲击力,此时桥墩两端为固定支座,可求出桥梁上部固定端的剪力.其次将桥梁上部固定端的剪力和摩擦反力比较,当上部固定端的剪力小于摩擦反力,即F(l-li)2(l+2li)/l3 < Gf,则假设成立,此时冲击修正系数kc3表达式为式(19);反之,假设不成立,此时墩顶会发生位移,冲击修正系数kc3表达式为(20).
4 算例与分析为验证本文方法的合理性,以汶川县登基沟处桥梁受泥石流大块石冲击力计算予以说明.汶川县登基沟泥石流沟所携带大块石为花岗岩,沟口桥墩采用C35钢筋混凝土浇筑而成.根据登基沟泥石流观测数据,取泥石流大块石速度为4.6 m/s研究泥石流大块石对桥墩的冲击力,其余影响块石与桥墩冲击力的相关计算参数见表 1、2.
| 表 1 块石相关计算参数 Table 1 Relevant calculation parameters of boulders |
| 表 2 桥墩相关计算参数 Table 2 Relevant calculation parameters of piers |
代入计算参数,可以求得kc1=0.262,kc2=0.633,kc3=0.401,kc=0.067,最大冲击力F=2 280.230 kN.如直接采用Hertz弹性理论进行计算,其理论冲击力F′=34 033.284 kN,远大于目前国内外通过现场观察所得的经验估计值[11-12].本例计算结果表明,在大块石冲击墩柱一类的冲击力计算中,系统材料和刚度对冲击力计算结果影响显著,综合考虑冲击系统特性计算出的冲击力仅为Hertz弹性理论计算结果的6.7%,所得计算冲击力更贴近实际情况,表 3为典型泥石流块石冲击灾害过程中冲击力预估值与Hertz理论计算值比较.
| 表 3 冲击力预估值与Hertz理论值[14] Table 3 Comparison between empirical estimates and theoretical values of Hertz[14] |
此外,以大块石速度为变量绘制了登基沟泥石流大块石冲击力随大块石冲击速度关系曲线,由图 3可以看出, 基于弹性材料的Hertz理论计算出的冲击力随冲击速度的增加而急剧增大,而本文的冲击力计算随速度的增加而增长较为平缓,这主要是由于计算采用的冲击系统材料为典型的弹塑性材料;与Mizuyama[10]和Yamaguchi[9]公式计算结果相比,本文冲击力计算结果偏小,主要是由于本文提出的计算公式综合考虑了冲击系统的材料及刚度特性.

|
图 3 泥石流块石冲击力与冲击速度关系曲线 Figure 3 Relationship between impact force and boulder velocity in debris flow |
由式(15)可知,冲击系统材料确定,冲击力计算中的材料修正系数随之确定.由于泥石流中常见块石弹性模量为10.5~135.5 GPa,泊松比为0.10~0.35;工程中常用混凝土弹性模量为22.0~32.5 GPa,泊松比为0.18~0.20.根据式(1)中等效模量表达式,可得等效模量为8.3~30.8 GPa.结合式(15)进行计算,绘制材料修正系数与等效模量的关系曲线.由图 4可以看出,材料修正系数随等效模量的增加而增加,其值在0.20~0.45.表明随系统材料等效模量的增加,系统弹性冲击特性愈加明显.
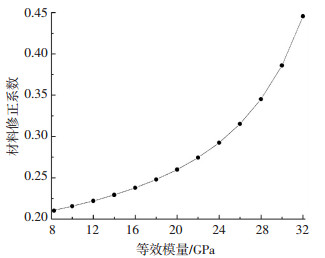
|
图 4 材料修正系数与等效模量关系曲线 Figure 4 Relationship between material correction coefficient and equivalent modulus |
由式(16)及图 5可知,球径比修正系数随球径比的增大而增加.计算表明n1=2时,kc2=0.859;n1=5时,kc2=0.960;n1=10时,kc2=0.981.可以看出,当0≤n1 < 2时,球径比修正系数增长显著;当2≤n1 < 5时,球径比修正系数增长相对缓慢;当5≤n1 < 10时,球径比修正系数增长变化不大;当n1≥10时,球径比修正系数基本稳定.表明当被冲击结构代表尺寸较小时,应重视构筑物尺寸对冲击力的影响.当其代表尺寸增加到一定程度时,可不再考虑构筑物尺寸大小对冲击力的折减效应.
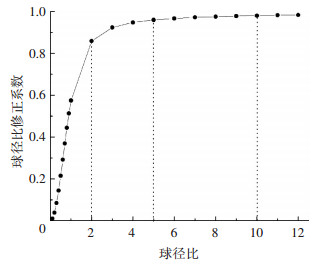
|
图 5 球径比修正系数与球径比关系曲线 Figure 5 Relationship between correction coefficient of ball diameter ratio and diameter ratio |
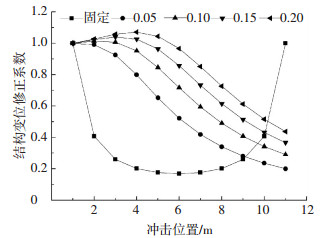
由式(19)、(20)及图 6可知,桥梁墩顶不同的位移方式对冲击力的影响显著不同.对于墩顶不发生位移的情况下,从桥墩底部至桥墩中部其修正系数逐渐减小,衰减速率逐步降低,在桥墩中部位置时修正系数达最小值;对于墩顶沿撞击方向发生了一定位移的情况下,结构变位修正系数不仅与冲击位置有关,也与桥梁上部结构作用于墩顶的摩擦力有关,上部结构提供的摩擦力越大,相应的结构变位修正系数越大,增长速率逐步降低.在上部结构一定的情况下,结构变位修正系数自墩底到墩顶的方向先增大后减小.
|
图中固定指墩顶无位移时不同冲击位置时的修正系数,其余带有数值的图例指墩顶有位移时,n2分别为0.05、0.10、0.15、0.20时不同冲击位置的修正系数. 图 6 结构变位修正系数与冲击位置关系曲线 Figure 6 Relationship between structure displacement correction coefficient and impact location |
1)冲击系统的材料性质、相对尺寸大小及冲击位置对冲击力影响显著,工程设计中应加以考虑.
2)综合考虑冲击系统的材料性质、相对尺寸大小及构筑物结构变位情况所计算出的最大冲击力远小于Hertz弹性碰撞理论所得的冲击力,更贴近实际情况.
3)本文提出的修正冲击力计算公式可弥补工程经验和模型试验方法确定修正参数主观性强、离散性大的不足.其严格按照力学原理推导,理论依据充分,参数明确,修正计算采用显示解,使用方便,计算结果更为贴近工程预估值,可为泥石流区地质灾害设计提供有效参考.
| [1] | ZENG Chao, CUI Peng, SU Zhiman, et al. Failure modes of reinforced concrete columns of buildings under debris flow impact[J]. Landslides, 2015, 12 (3) : 561-571. DOI: 10.1007/s10346-014-0490-0 |
| [2] |
张晨, 王清, 张文, 等. 基于神经网络对泥石流危险范围的研究[J].
哈尔滨工业大学学报, 2010, 42 (10) : 1642-1645.
ZHANG Chen, WANG Qing, ZHANG Wen, et al. Prediction on hazardous areas of debris flow based on neural network[J]. Journal of Harbin Institute of Technology, 2010, 42 (10) : 1642-1645. |
| [3] | HE Siming, LIU Wei, LI Xinpo. Prediction of impact force of debris flows based on distribution and size of particles[J]. Environmental Earth Sciencess, 2016, 75 (4) : 1-8. DOI: 10.1007/s12665-015-5180-2 |
| [4] |
于献彬, 陈晓清, 李昆, 等. 复合型拦砂坝受泥石流大块石冲击作用的动力响应[J].
施工技术, 2015, 44 (24) : 114-119.
YU Xianbin, CHEN Xiaoqing, LI Kun, et al. Compound dam dynamic response to the impact of massive stone in debris flow[J]. Construction Technology, 2015, 44 (24) : 114-119. |
| [5] |
胡凯衡, 韦方强, 洪勇, 等. 泥石流冲击力的野外测量[J].
岩石力学与工程学报, 2006, 25 (S1) : 2813-2819.
HU Kaiheng, WEI Fangqiang, HONG Yong, et al. Field measurement of impact force of debris flow[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25 (S1) : 2813-2819. |
| [6] |
章书成, HUNGR O.泥石流中巨石冲击力计算[C]//泥石流观测与研究.北京:科学出版社, 1996:67-72.
ZHANG Shucheng, HUNGR O.The calculation of impact force of boulders in debris flow[C]//Debris Flow Observation and Research. Beijing: Science Press, 1996:67-72. |
| [7] | WANG Quancai, CHEN Jian, WANG Hao, et al. Impact force of boulders conveyed in debris flows on bridge piers and anti-collision measures[J]. International Journal of Geohazards and Environment, 2016, 2 (2) : 72-81. DOI: 10.15273/ijge.2016.02.008 |
| [8] | THORNTON C. Coefficient of restitution for collinear collisions of elastic perfectly plastic spheres[J]. Journal of Applied Mechanics, 1997, 64 (2) : 383-386. DOI: 10.1115/1.2787319 |
| [9] | YAMAGUCHI L. Erosion control engineering[M]. Tokyo: Society of Erosion Control Engineering, 1985 : 32 -45. |
| [10] | MIZUYAMA T. Evaluation of impact of debris flow on check dams[J]. Journal of the Japan Society of Erosion Control Engineering, 1979, 32 (1) : 269-274. |
| [11] | BRACCESI C, LANDI L. A general elastic-plastic approach to impact analisys for stress state limit evaluation in ball screw bearings return system[J]. International Journal of Impact Engineering, 2007, 34 (7) : 1272-1285. DOI: 10.1016/j.ijimpeng.2006.06.005 |
| [12] |
黄宏斌, 杨凯钧, 赖邵文. 土石流对梳子坝撞击力之研究[J].
台湾水利, 2006, 55 (1) : 41-58.
HUANG Hongbing, YANG Kaijun, LAI Shaowen. Impact force of debris flow on filter dam[J]. Journal of Taiwan Water Conservancy, 2006, 55 (1) : 41-58. |
| [13] | RAOUS M, JEAN M, MOREAU J. Contact mechanics[J]. Springer Netherlands, 2009, 108 (4) : 464-468. |
| [14] |
周必凡, 李德基, 罗德富, 等.
泥石流防治指南[M]. 北京: 科学出版社, 1991 : 65 -68.
ZHOU Bifan, LI Deji, LUO Defu, et al. Prevention and control guidelines of debris flow[M]. Beijing: Science Press, 1991 : 65 -68. |
| [15] |
何思明, 李新坡, 吴永. 考虑弹塑性变形的泥石流大块石冲击力计算[J].
岩石力学与工程学报, 2007, 26 (8) : 1664-1669.
HE Siming, LI Xinpo, WU Yong. Calculation of impact force of outrunner blocks in debris flow considering elastoplastic deformation[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26 (8) : 1664-1669. |
| [16] | ZHANG Xiang, VU-QUOC L. Modeling the dependence of the coefficient of restitution on the impact velocity in elasto-plastic collisions[J]. International Journal of Impact Engineering, 2002, 27 (3) : 317-341. DOI: 10.1016/S0734-743X(01)00052-5 |
| [17] | BRIZMER V, KLIGERMAN Y, ETSION I. The effect of contact conditions and material properties on the elasticity terminus of a spherical contact[J]. International Journal of Solids and Structures, 2006, 43 (18/19) : 5736-5749. DOI: 10.1016/j.ijsolstr.2005.07.034 |
| [18] |
曾聪, 陶忠, 潘文, 等. PTFE-不锈钢摩擦滑移隔震支座摩擦系数的影响因素研究[J].
工程抗震与加固改造, 2009, 31 (1) : 58-63.
ZENG Cong, TAO Zhong, PAN Wen, et al. Research of the influence factors of the friction coefficient between PTFE and stainless steelPlate of FPE[J]. Earthquake Resistant Engineering and Retrofitting, 2009, 31 (1) : 58-63. |
 2017, Vol. 49
2017, Vol. 49


