收稿日期: 2016-03-04
基金项目: 国家自然科学基金(51408150); 中央高校基本科研业务费专项资金(2014KJ044)
作者简介: 强旭红(1984-),女,博士,助理教授;
罗永峰(1957-),男,教授,博士生导师
Mechanical properties of high strength steels S460 and S690 after fire
College of Civil Engineering, Tongji University, Shanghai 200092, China
目前,对于高强钢的定义,欧洲钢结构设计规范Eurocode 3(EC3)[1]定义高强钢的名义屈服强度不小于460 MPa;澳大利亚规范AS 4100[2]定义高强钢的名义屈服强度大于450 MPa;香港规范[3]定义高强钢的名义屈服强度在460~690 MPa;中国国家标准《钢分类》[4]定义屈服强度大于等于420 MPa的钢材为高强钢.钢材在常温下具有良好的力学性能,随着温度升高,钢材的力学性能显著降低.自美国“911”恐怖事件后,研究火灾下材料退化、热约束及结构构件的偶然移除对结构性能的综合影响成为结构工程领域的当务之急.目前的研究尚主要针对常规强度的结构钢(普通钢)[5-7],对于高强钢火灾下力学性能的研究有限,涉及的强度等级主要有S460[8-14]和BISPLATE 80[15];尚未有学者对高强钢火灾后的力学性能进行研究,即使对于普通钢火灾后力学性能的研究也很有限[9-10, 16-18].英国规范BS 5950-8(2003)附录B[19]针对普通钢火灾后力学性能和继续使用提出若干建议:若火灾后热处理钢和铸钢的变形在限值内,则可以继续使用;普通钢S235和S275火灾后可恢复其常温下(未过火)90%的力学性能;当过火温度超过600 ℃时,S355冷却后的强度可恢复至常温(未过火)时的75%以上.但对于高强钢,世界范围内现行的钢结构设计规范还没有给出任何相关建议.
可靠的高强钢火灾后性能数据的缺失导致高强钢结构火灾后性能的检测与鉴定缺乏重要依据,这将造成不必要的经济损失.因此,BS 5950[19]和EC3 part1-2[1]等现行钢结构设计规范对高强钢火灾后的力学性能提出针对性建议势在必行.本文对欧标高强钢S460和S690进行的火灾后拉伸试验旨在揭示S460和S690火灾后的弹性模量、屈服强度及极限强度的退化程度,并与现有研究成果和现行钢结构设计规范中的其他等级钢材进行对比.分别给出高强钢S460和S690火灾后力学性能剩余程度的预测公式,并验证其准确性.
1 试验 1.1 试验设备 火灾试验在可控温的电热炉中完成(如图 1所示).拉伸试验通过Gleeble 3800系统进行,该系统是全数字闭环控制热与力学耦合测试系统,如图 2、3所示.Gleeble 3800系统是力学与热学耦合的一体化系统,最大可施加20 t的压力或10 t的拉力.本试验采用非接触式激光变形测量仪测量试件的应变,通过QuikSim软件预先设定的程序控制试验过程.试验过程中得出的所有试验数据由电脑存储,并可由屏幕实时显示进行试验监测.
1.2 试验材料及试件设计 试验试件分别由名义厚度为5 mm的S460NL和S690QL钢板上切割而来.S460NL是一种符合欧洲标准EN 10025-3[20]的高强度结构用钢.S460NL是钢材等级名称缩写,S指结构用钢,460指名义屈服强度为460 MPa,N指采用标准化轧制,L指低温韧性.S690QL钢是一种符合欧洲标准EN 10025-6[21]的高强度结构用钢.该钢材经过淬火回火技术处理,具有良好的抗弯性和可焊性.类似地,S690QL是钢材等级名称缩写,S指结构用钢,690指名义屈服强度为690 MPa,Q指淬火回火技术,L指低温韧性.
本试验所用高强钢S460和S690的化学成分见表 1.试件的形状和尺寸符合欧洲标准EN 10002-5[22]和美国标准ASTM E21-09[23]的要求.为将试件固定到Gleeble 3800系统的夹具上,在试件的两端预留孔洞,以便固定试件(如图 4所示).
表 1

表 1 高强钢S460NL和S690QL的化学组成(质量分数)
Table 1 Chemical composition of S460NL and S690QL
| % |
| 高强钢 |
C |
Si |
Mn |
P |
S |
Cr |
Cu |
N |
Nb |
Ni |
Ti |
V |
Al |
Mo |
| S460NL |
0.172 |
0.483 |
1.500 |
0.012 |
0.005 |
0.020 |
0.025 |
0.005 1 |
0.046 |
0.018 |
0.002 |
0.087 |
0.037 |
0.002 |
| S690QL |
0.160 |
0.210 |
0.850 |
0.012 |
0.001 |
0.350 |
0.030 |
0.002 6 |
0.025 |
0.050 |
0.006 |
0 |
0.093 |
0.200 |
|
表 1 高强钢S460NL和S690QL的化学组成(质量分数)
Table 1 Chemical composition of S460NL and S690QL
|
1.3 试验方法 常用的评估钢材高温力学性能的方法是进行稳态或者瞬态火灾拉伸试验.与瞬态火灾试验方法相比,稳态火灾试验方法更为常用,因为稳态火灾试验操作相对容易并且能直接获得材料的应力-应变曲线.因此,采用稳态火灾试验方法对S460和S690火灾后的力学性能进行研究,即试件升温至指定温度后自然冷却至常温,随后对试件进行拉伸试验.
1.4 试验步骤 试件在电热炉中由常温升温至指定温度,为模拟自然火灾,升温速率取10 ℃/min.对于S460,选取11个火灾温度:300、400、500、600、650、700、750、800、850、900及1 000 ℃;对于S690,还选取火灾温度100和200 ℃.试件升温至指定温度后,持温约10 min,使试件中部的温度分布均匀,随后自然冷却至常温,在常温下对试件施加拉力直至破坏.采用应变控制的方法施加荷载,应变率为0.005 min-1,满足ASTM E21-09[23]的相关规定.为比较过火温度对高强钢火灾后力学性能的影响,同时对试件进行常温下(未过火)的拉伸试验.
2 试验结果 S460和S690火灾后的应力-应变曲线分别如图 5、6所示,本节在高强钢火灾后应力-应变曲线的基础上对其火灾后力学性能进行研究.S690的试验结果表明,过火温度为100和200 ℃时,其冷却至室温后的力学性能与常温时(未过火)相比几乎无变化.因此,在对S460火灾后力学性能进行研究时,未选取100和200 ℃作为过火温度.
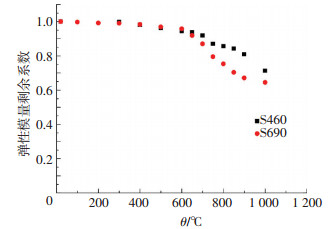
2.1 弹性模量 弹性模量是影响钢结构承载能力的重要参数之一.高温下,钢材的弹性模量取决于相应温度的应力-应变曲线;类似地,钢材火灾后的弹性模量也由钢材火灾后的应力-应变曲线得到.钢材火灾后力学性能的剩余程度常用剩余系数来评估,弹性模量剩余系数是指钢材火灾后的弹性模量与常温下(未过火)弹性模量的比值.试验得到的高强钢S460和S690火灾后的弹性模量和弹性模量剩余系数见表 2,弹性模量剩余系数随过火高温的变化见图 7.
表 2

表 2 火灾后弹性模量和弹性模量剩余系数
Table 2 Post-fire elastic modulus and residual factors
| θ/℃ |
S460 |
|
S690 |
| 弹性模量/MPa |
剩余系数 |
弹性模量/MPa |
剩余系数 |
| 20 |
202 619 |
1.000 |
|
212 490 |
1.000 |
| 100 |
- |
- |
211 800 |
0.997 |
| 200 |
- |
- |
210 808 |
0.992 |
| 300 |
202 300 |
0.998 |
210 400 |
0.990 |
| 400 |
198 870 |
0.981 |
208 900 |
0.983 |
| 500 |
194 910 |
0.962 |
205 900 |
0.969 |
| 600 |
191 320 |
0.944 |
203 500 |
0.958 |
| 650 |
190 000 |
0.938 |
195 250 |
0.919 |
| 700 |
186 140 |
0.919 |
184 761 |
0.870 |
| 750 |
176 184 |
0.870 |
168 879 |
0.795 |
| 800 |
173 660 |
0.857 |
160 010 |
0.753 |
| 850 |
170 780 |
0.843 |
149 520 |
0.704 |
| 900 |
163 980 |
0.809 |
142 538 |
0.671 |
| 1 000 |
144 470 |
0.713 |
137 063 |
0.645 |
|
表 2 火灾后弹性模量和弹性模量剩余系数
Table 2 Post-fire elastic modulus and residual factors
|
由图 7可以看出:当过火温度低于600 ℃时,S460和S690冷却后的弹性模量与常温下(未过火)相同;当过火温度超过600 ℃后,S460和S690冷却后的弹性模量显著降低,且S690的降幅更大,这是由S460N和S690Q制造过程中不同的淬火回火技术造成的.值得注意的是,当过火温度为800 ℃时,S460和S690冷却后的弹性模量可达常温下(未过火)的75%;即使过火温度高达1 000 ℃,S460和S690冷却后的弹性模量仍可达常温下(未过火)的60%.
2.2 屈服强度 常温下,一般取0.2%作为钢材的名义应变,取此应变对应的应力作为钢材的名义屈服强度.高温下,由于没有明确统一的定义,有些学者采用0.5%、1.5%及2.0%分别作为名义应变,取其对应的应力为钢材的名义屈服强度[8-9, 15].本文研究过火温度对S460和S690火灾后名义屈服强度的影响(名义应变分别取0.2%、0.5%、1.5%及2.0%),并对比以上4个名义应变对应的名义屈服强度剩余情况的异同.名义应变0.2%对应的名义屈服强度(f0.2)是由应力-应变曲线与原点处切线平移到0.2%应变处的直线的交点确定;而0.5%、1.5%及2.0%应变所对应的屈服强度是由其应变水平处的垂直线与应力-应变曲线的交点确定.
钢材的屈服强度剩余系数是指钢材火灾后的屈服强度与常温下(未过火)屈服强度的比值.试件经拉伸试验得到的4个不同名义应变对应的名义屈服强度见表 3, 屈服强度剩余系数见表 4,屈服强度剩余系数随过火高温的变化如图 8所示.
表 3

表 3 火灾后不同名义应变条件下的屈服强度
Table 3 Post-fire yield strengthMPa
| θ/℃ |
S460 |
|
S690 |
| 0.2% |
0.5% |
1.5% |
2% |
0.2% |
0.5% |
1.5% |
2% |
| 20 |
490 |
495 |
490 |
524 |
|
789 |
806 |
784 |
786 |
| 100 |
- |
- |
- |
- |
787 |
801 |
787 |
787 |
| 200 |
- |
- |
- |
- |
787 |
782 |
789 |
789 |
| 300 |
490 |
496 |
495 |
521 |
785 |
781 |
781 |
781 |
| 400 |
489 |
489 |
495 |
498 |
786 |
806 |
788 |
786 |
| 500 |
494 |
496 |
490 |
509 |
786 |
807 |
790 |
790 |
| 600 |
480 |
478 |
492 |
506 |
785 |
802 |
783 |
786 |
| 650 |
466 |
472 |
474 |
473 |
793 |
800 |
769 |
783 |
| 700 |
474 |
474 |
471 |
472 |
705 |
707 |
702 |
698 |
| 750 |
442 |
439 |
430 |
455 |
591 |
591 |
603 |
608 |
| 800 |
428 |
425 |
437 |
432 |
484 |
484 |
486 |
486 |
| 850 |
427 |
427 |
428 |
441 |
420 |
420 |
417 |
418 |
| 900 |
427 |
424 |
425 |
426 |
320 |
321 |
375 |
394 |
| 1 000 |
374 |
375 |
387 |
400 |
301 |
301 |
328 |
351 |
|
表 3 火灾后不同名义应变条件下的屈服强度
Table 3 Post-fire yield strengthMPa
|
表 4

表 4 火灾后屈服强度剩余系数
Table 4 Post-fire yield strength residual factors
| θ/℃ |
S460 |
|
S690 |
| 0.2% |
0.5% |
1.5% |
2% |
0.2% |
0.5% |
1.5% |
2% |
| 20 |
1.000 |
1.000 |
1.000 |
1.000 |
|
1.000 |
1.000 |
1.000 |
1.000 |
| 100 |
- |
- |
- |
- |
0.998 |
0.994 |
1.004 |
1.002 |
| 200 |
- |
- |
- |
- |
0.998 |
0.971 |
1.006 |
1.004 |
| 300 |
1.000 |
1.002 |
1.010 |
0.995 |
0.995 |
0.970 |
0.997 |
0.995 |
| 400 |
0.997 |
0.988 |
1.011 |
0.951 |
0.997 |
1.000 |
1.005 |
1.001 |
| 500 |
1.007 |
1.002 |
1.000 |
0.972 |
0.997 |
1.002 |
1.007 |
1.005 |
| 600 |
0.980 |
0.966 |
1.005 |
0.965 |
0.995 |
0.995 |
0.999 |
1.001 |
| 650 |
0.950 |
0.954 |
0.968 |
0.903 |
1.006 |
0.993 |
0.981 |
0.997 |
| 700 |
0.968 |
0.959 |
0.960 |
0.901 |
0.894 |
0.877 |
0.895 |
0.889 |
| 750 |
0.901 |
0.887 |
0.876 |
0.868 |
0.749 |
0.733 |
0.769 |
0.775 |
| 800 |
0.874 |
0.858 |
0.891 |
0.824 |
0.614 |
0.600 |
0.619 |
0.618 |
| 850 |
0.871 |
0.863 |
0.873 |
0.843 |
0.532 |
0.521 |
0.531 |
0.532 |
| 900 |
0.871 |
0.858 |
0.867 |
0.813 |
0.405 |
0.399 |
0.478 |
0.502 |
| 1 000 |
0.763 |
0.758 |
0.790 |
0.764 |
0.381 |
0.373 |
0.419 |
0.447 |
|
表 4 火灾后屈服强度剩余系数
Table 4 Post-fire yield strength residual factors
|
由图 8可以看出,当过火温度低于600 ℃时,过火高温对S460和S690冷却后的屈服强度几乎无影响;当过火温度超过600 ℃后,S460的屈服强度剩余系数高于S690;即使过火温度高达1 000 ℃,S460冷却后仍可恢复其常温下(未过火)75%的屈服强度,这是由S460N和S690Q制造过程中不同的淬火回火技术造成的.试验结果表明,若火灾温度低于600 ℃,S460和S690冷却后的屈服强度与常温时(未过火)相同,这对高强钢火灾后的再利用十分有利.出于安全考虑,若采用高强钢S460或S690的建筑结构经历的火灾温度在600 ℃以下,建议灾后S460和S690的名义屈服强度取常温下(未过火)的90%.因此,采用高强钢S460和S690的构件若经历的火灾温度在600 ℃以下,同时构件的平直度在限值内,其在火灾后可继续使用.
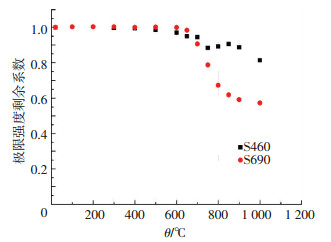
2.3 极限强度 钢材的极限强度剩余系数是指钢材火灾后的极限强度与常温下(未过火)极限强度的比值.试验得出的高强钢火灾后极限强度剩余系数见表 5和图 9.结果表明,当过火温度不超过600 ℃时,过火高温对S460和S690冷却后的极限强度几乎无影响;当过火温度超过600 ℃后,S460的极限强度剩余系数高于S690;即使过火温度高达1 000 ℃,S460冷却后的极限强度可恢复其常温下(未过火)的80%,而S690仅剩余55%,这同样是由S460N和S690Q制造过程中不同的淬火回火技术造成的.
表 5

表 5 火灾后极限强度和极限强度剩余系数
Table 5 Post-fire ultimate strength and residual factors
| θ/℃ |
S460 |
|
S690 |
| 极限强度/MPa |
剩余系数 |
极限强度/MPa |
剩余系数 |
| 20 |
640 |
1.000 |
|
820 |
1.000 |
| 100 |
- |
- |
823 |
1.003 |
| 200 |
- |
- |
823 |
1.003 |
| 300 |
638 |
0.996 |
822 |
1.002 |
| 400 |
637 |
0.995 |
820 |
0.999 |
| 500 |
631 |
0.985 |
821 |
1.001 |
| 600 |
621 |
0.970 |
820 |
1.000 |
| 650 |
608 |
0.950 |
807 |
0.983 |
| 700 |
605 |
0.945 |
743 |
0.906 |
| 750 |
566 |
0.884 |
646 |
0.788 |
| 800 |
571 |
0.892 |
552 |
0.673 |
| 850 |
580 |
0.906 |
507 |
0.619 |
| 900 |
568 |
0.887 |
485 |
0.592 |
| 1 000 |
521 |
0.814 |
470 |
0.573 |
|
表 5 火灾后极限强度和极限强度剩余系数
Table 5 Post-fire ultimate strength and residual factors
|
2.4 延性 钢材的延性取决于钢材破坏前的变形能力,通过图 5、6中试件断裂时的应变可看出,S460在常温下(未过火)和过火温度较低时的延性均优于S690.但当过火温度超过750 ℃时,两种钢材冷却后的延性相仿.值得注意的是,当过火温度为750 ℃时,S690冷却后的延性高于常温(未过火)时,而S460未发现此现象.图 10、11列出高强钢常温(未过火)和火灾后的破坏模式,可以看出,所有试件在破坏前均发生颈缩现象,无试件脆性破坏.这表明高强钢火灾后具备一定的延性,可适当保证结构火灾后的安全性.
2.5 对比分析 现有研究鲜有涉及钢材火灾下和火灾后力学性能,BS 5950-8(2003)附录B[19]对火灾后普通钢的继续使用提出相关建议;BS 5950对铸钢和预应力钢筋的火灾下和火灾后力学性能也提出相关建议,但并未提及高强钢.世界范围内现行的其他钢结构设计规范尚未对钢材火灾后的继续使用给出建议.Outinen[9-10]从升温至710 ℃的S355和S350上截取试件,对试件进行常温下拉伸试验.基于试验结果建议:若钢结构火灾后的变形满足限值要求,材料的强度仍可满足要求.遗憾的是,现阶段定量的钢材火灾后材性数据仍十分匮乏.本文的试验研究表明,高强钢S460和S690火灾后的强度剩余程度与普通钢不同.当过火温度不超过600 ℃时,高强钢冷却后可恢复其常温下(未过火)的力学性能.出于安全考虑,建议火灾后S460和S690的名义屈服强度取常温下(未过火)的90%;当过火温度超过600 ℃时,S460冷却后的屈服强度和极限强度可恢复至常温下(未过火)的75%;S690冷却后的屈服强度和极限强度则退化较多.因此,采用BS 5950针对普通钢提出的建议预测高强钢火灾后的力学性能是十分危险的,应对高强钢火灾后力学性能提出针对性的预测公式,对高强钢火灾后可否继续使用提出针对性的建议.
3 预测公式 由于过火温度是钢材火灾后力学性能退化的主要因素,各力学性能剩余系数是试件过火温度θ的函数.对于S460火灾后力学性能的预测,给出两种选择,一种便于实际应用,另一种用于精确预测.由图 12~20可以看出,建议公式与试验结果拟合较好,因此建议公式可以准确预测高强钢S460和S690的火灾后力学性能.
3.1 弹性模量 3.1.1 S460 针对S460火灾后弹性模量提出的两种预测公式如下
选择1:
|
$\begin{array}{l}
\frac{{{E_\theta }}}{{{E_{20}}}} = - 2.69 \times {10^{ - 7}}{\theta ^2} + 6.55 \times {10^{ - 5}}\theta + 0.999,\\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;20 \le \theta \le 600;
\end{array}$
|
(1) |
|
$\begin{array}{l}
\frac{{{E_\theta }}}{{{E_{20}}}} = 0.947 - \frac{{{{\left( {\theta - 600} \right)}^{1.618}}}}{{68.84\theta }},\\
\;\;\;\;\;\;\;\;\;\;600 < \theta \le 800;
\end{array}$
|
(2) |
|
$\begin{array}{l}
\frac{{{E_\theta }}}{{{E_{20}}}} = - 2.545 \times {10^{ - 6}}{\theta ^2} + 3.856 \times {10^{ - 3}}\theta - 0.598,\\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;800 < \theta \le 1{\rm{ }}000.
\end{array}$
|
(3) |
预测公式(1)~(3)与试验结果的对比见图 12,可以看出,预测公式与试验结果吻合.
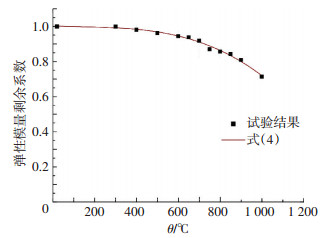
选择2:
|
$\begin{array}{l}
\frac{{{E_\theta }}}{{{E_{20}}}} = - 3.84 \times {10^{ - 10}}{\theta ^3} + 1.43 \times {10^{ - 7}}{\theta ^2} - 4.18 \times \\
\;\;\;\;\;\;\;\;\;{10^{ - 5}}\theta + 1.00{\rm{,}}20 \le \theta \le 1{\rm{ }}000.
\end{array}$
|
(4) |
选择2采用统一的公式对S460火灾后力学性能进行预测,图 13表明预测公式(4)与试验结果吻合.预测公式(1)~(3)精度较高,如所需预测公式形式简单,推荐采用式(4).
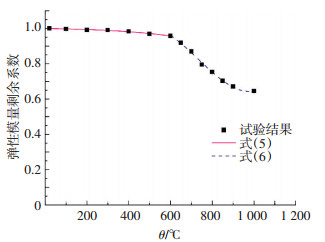
3.1.2 S690 预测公式(5)、(6)与试验结果的对比见图 14.可以看出,预测公式与试验结果吻合,同时其形式简单,因此,建议采用式(5)、(6)对S690火灾后的弹性模量剩余程度进行预测.
|
$\begin{array}{l}
\frac{{{E_\theta }}}{{{E_{20}}}} = - 1.52 \times {10^{ - 10}}{\theta ^3} + 2.70 \times {10^{ - 8}}{\theta ^2} - 3.35 \times \\
\;\;\;\;\;\;\;{10^{ - 5}}\theta + 1,20 \le \theta \le 600;
\end{array}$
|
(5) |
|
$\begin{array}{l}
\frac{{{E_\theta }}}{{{E_{20}}}} = 6.27 \times {10^{ - 9}}{\theta ^3} - 1.38 \times {10^{ - 5}}{\theta ^2} + 8.95 \times {10^{ - 3}}\theta - \\
\;\;\;\;\;\;\;\;0.806,600 < \theta \le {\rm{ }}1{\rm{ }}000.
\end{array}$
|
(6) |
3.2 屈服强度 与常温下钢材的名义应变相应,建议取0.2%作为火灾后钢材的名义应变,本文在拟合屈服强度预测公式时采用0.2%名义应变的试验数据.
3.2.1 S460 选择1:
|
$\begin{array}{l}
\frac{{{f_{y\theta }}}}{{{f_{y20}}}} = - 1.19 \times {10^{ - 9}}{\theta ^3} + 1.03 \times {10^{ - 6}}{\theta ^2} + 2.25 \times \\
\;\;\;\;\;\;{10^{ - 4}}\theta + 1.004,20 \le \theta \le 800;
\end{array}$
|
(7) |
|
$\begin{array}{l}
\frac{{{f_{y\theta }}}}{{{f_{y20}}}} = 0.876 - \frac{{{{\left( {\theta - 800} \right)}^{3.634}}}}{{2.048 \times {{10}^6}\theta }},\\
\;\;\;\;\;\;\;\;\;\;800 < \theta \le 1000.
\end{array}$
|
(8) |
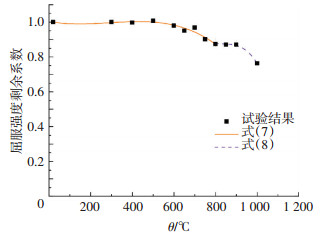
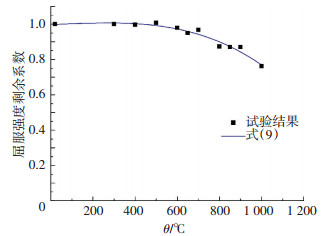
预测公式(7)、(8)与试验结果的对比见图 15.可以看出,预测公式与试验结果吻合.为简化提出式(9),其与试验结果的对比见图 16.由图 15、16可以看出,式(7)、(8)更精准,式(9)更简洁,使用时可根据需要进行选择.
选择2:
|
$\begin{array}{l}
\frac{{{f_{y\theta }}}}{{{f_{y20}}}} = - 3.24 \times {10^{ - 10}}{\theta ^3} + 4.98 \times {10^{ - 8}}{\theta ^2} + 4.52 \times {10^{ - 5}}\theta + \\
\;\;\;\;\;\;0.998,20 \le \theta \le 1{\rm{ }}000.
\end{array}$
|
(9) |
3.2.2 S690 预测公式(10)、(11)与试验结果的对比见图 17.可以看出,预测公式与试验结果吻合,同时其形式简单,因此,建议采用式(10)、(11)对S690火灾后的屈服强度剩余程度进行预测.
|
$\begin{array}{l}
\frac{{{f_{y\theta }}}}{{{f_{y20}}}} = 1.0 - \frac{{{{\left( {\theta - 20} \right)}^{1.584}}}}{{9{\rm{ }}957\theta }},\\
\;\;\;\;\;\;\;\;20 \le \theta \le 650;
\end{array}$
|
(10) |
|
$\begin{array}{l}
\frac{{{f_{y\theta }}}}{{{f_{y20}}}} = 1.80 \times {10^{ - 8}}{\theta ^3} - 4.03 \times {10^{ - 5}}\theta + 2.74 \times \\
\;\;\;\;\;\;\;{10^{ - 2}}\theta - 4.711,650 \le \theta \le 1{\rm{ }}000.
\end{array}$
|
(11) |
3.3 极限强度 3.3.1 S460 选择1:
|
$\begin{array}{l}
\frac{{{f_{u\theta }}}}{{{f_{u20}}}} = - 1.24 \times {10^{ - 9}}{\theta ^3} + 1.07 \times {10^{ - 6}}{\theta ^2} - 2.54 \times {10^{ - 4}}\theta + \\
\;\;\;\;\;\;\;\;\;1.005,20 \le \theta \le 750;
\end{array}$
|
(12) |
|
$\begin{array}{l}
\frac{{{f_{u\theta }}}}{{{f_{u20}}}} = - 3.09 \times {10^{ - 6}}{\theta ^2} + 5.14 \times {10^{ - 3}}\theta - 1.235,\\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;750 < \theta \le 1{\rm{ }}000.
\end{array}$
|
(13) |
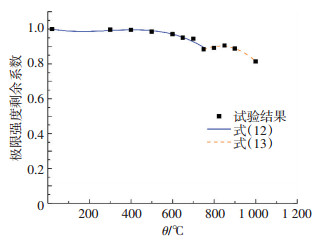
预测公式(12)、(13)与试验结果的对比见图 18.可以看出,预测公式与试验结果吻合.
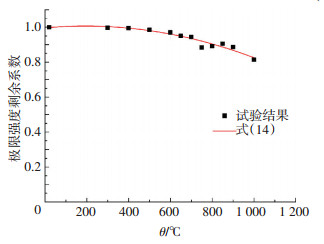
为简化提出式(14),其与试验结果的对比见图 19.由图 18、19可以看出,式(12)、(13)更精准,式(14)更简洁,使用时可根据需求进行选择.
选择2:
|
$\begin{array}{l}
\frac{{{f_{u\theta }}}}{{{f_{u20}}}} = - 2.79 \times {10^{ - 7}}{\theta ^2} + 1.08 \times {10^{ - 4}}\theta + 0.996,\\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;20 \le \theta \le 1{\rm{ }}000.
\end{array}$
|
(14) |
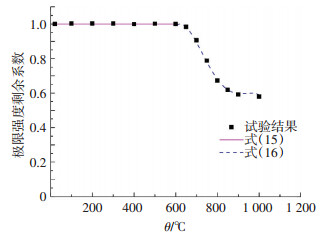
3.3.2 S690 预测公式(15)、(16)与试验结果的对比见图 20.可以看出,预测公式与试验结果吻合,同时其形式简单,因此,建议采用式(15)、(16)对S690火灾后的极限强度剩余程度进行预测.
|
$\frac{{{f_{u\theta }}}}{{{f_{u20}}}} = 1.000,20 \le \theta \le 600;$
|
(15) |
|
$\begin{array}{l}
\frac{{{f_{u\theta }}}}{{{f_{u20}}}} = - 1.24 \times {10^{ - 10}}{\theta ^4} + 4.13 \times {10^{ - 7}}{\theta ^3} - {\rm{ }}5.077 \times \\
\;\;\;\;\;\;\;\;\;{10^{ - 4}}{\theta ^2} + 0.271\theta - 52.21,600 \le \theta \le 1{\rm{ }}000.
\end{array}$
|
(16) |
4 结论 钢材火灾后的力学性能取决于钢材的等级和生产加工工艺,因此BS 5950针对普通钢火灾后力学性能和可否继续使用提出的建议并不适用于高强钢,应对高强钢提出针对性建议.现有的针对高强钢火灾后力学性能的研究非常有限,各国现行钢结构设计规范也未对高强钢火灾后力学性能提出针对性建议,本研究对这方面的研究起到抛砖引玉作用.研究表明,当过火温度低于600 ℃时,S460和S690冷却后可恢复其基本力学性能.此时,出于安全考虑,若采用高强钢S460或S690的建筑结构所经历的火灾温度在600 ℃以下,建议灾后S460和S690的名义屈服强度取其常温下(未过火)的90%.为便于评估S460和S690过火温度超过600 ℃甚至达到1 000 ℃冷却后的力学性能,本文提出一系列公式用以预测高强钢火灾后的弹性模量、屈服强度及极限强度的剩余情况,通过与试验结果的对比,验证预测公式的准确性,为高强钢结构火灾后性能的检测鉴定和可否继续使用提供理论依据,也为各国相关设计规范的修订提供参考.











 2017, Vol. 49
2017, Vol. 49


