大型挠性航天器在轨服务时,因天线结构尺寸大、质量轻、柔性大等多方面因素引起的弹性变形会直接影响天线反射面的形面精度、天线指向以及卫星的位置和姿态,甚至可能致使天线失效而不能顺利工作[1].天线的弹性变形已经成为大型挠性航天器动力学研究中不可忽略的因素.目前国内外针对星载柔性天线的动力耦合因素研究尚少,一般只针对天线的关键部件进行结构有限元分析.Theunissen等[2]利用有限元方法,得到了空间环境载荷作用下天线反射面位移场并预测了反射面的形面精度;蒋尔进[3]对既定类型的圆抛物面天线进行了计算和分析. Sreekantamurthy等[4]利用非线性结构动力学方法分析了抛物面天线反射面的结构动力学特性.Mobrem等[5]对空间可展开天线的质量特性、固有频率和振型做了详细研究,并讨论热变形、装配误差和外界扰动对天线膜面精度的影响.Datashvili等[6]建立了大口径天线非线性有限元模型,得到了天线结构的静力学、模态和屈曲特性.此外,目前针对天线指向精度的研究多为考虑各因素对其静态指向精度影响的分析[7-8].潘博等[9]考虑姿态控制误差和展开机构锁定误差的影响得到了综合静态误差;哈尔滨工业大学研究了空间热载荷作用、柔性关节动态误差、铰链间隙等对星载天线运动精度的影响[10-12].
星载天线的动态指向、大角度机动等刚体运动过程,将激起天线结构较大幅值弹性变形,其弹性振动又将作为整个卫星姿态运动的扰动源加剧其自身的弹性振动,因此,在带挠性反射面的星载天线动力学分析中,为提高天线的动态指向精度和相位中心的稳定性,考虑天线结构挠性对航天器调姿过程中焦点动态响应的影响具有重要意义.本文首先探究了大型挠性抛物面天线在运动过程中几何焦点的求解方法,通过建立有限元模型求解挠性天线的固有频率和振型,研究了挠性航天器的结构动力学特性,并利用整星有限元模型和多体动力学软件建立航天器零次刚柔耦合动力学模型,最后对航天器姿态调整过程动态响应进行了数值仿真求解.
1 抛物面天线几何焦点天线的相位中心对于天线在馈源放置、测距、定位和成像等方面都具有重要意义.为实现反射面天线高增益和低副瓣电平的目标,必须把馈源天线的相位中心放置在反射面天线的焦点处[13].抛物面天线多使用喇叭天线作为馈源,对于不存在严格相位中心的喇叭天线,工程上需要确定一个近似相位中心与抛物面焦点重合[14].故而,为研究星体运动过程中受刚柔耦合作用影响其相位中心的变化情况,建立求解抛物面天线动态几何焦点的数学模型.
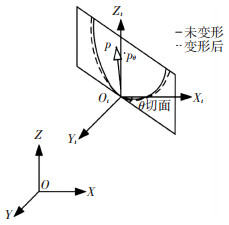
如图 1所示,全局参考坐标系为O-XYZ,在整星上建立体坐标系Ot-XtYtZt.整星的位姿调整可由旋转和平移矢量合成的六元组v=(α, β, γ, x, y, z)表示,其中,α、β、γ分别为Ot-XtYtZt相对于O-XYZ的滚动角、俯仰角和偏转角,x、y、z为Ot在O-XYZ中的坐标.利用全局坐标系O-XYZ中所得的天线肋条坐标值R0,通过坐标变换得到体坐标系Ot-XtYtZt下肋条某一时刻的采样点坐标值Rt.例如调姿过程为先绕X轴转α角,绕Y轴转β角,绕Z轴转γ角,然后沿X轴平移x,沿Y轴平移y,沿Z轴平移z.那么有
| ${\mathit{\boldsymbol{R}}_0} = {\mathit{\boldsymbol{R}}_\tau }\mathit{\boldsymbol{{\rm T}}} + \Delta \mathit{\boldsymbol{{\rm T}}},$ | (1) |
| $\begin{array}{l} \Delta \mathit{\boldsymbol{T}} = \left( {x,y,z} \right),\\ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {\cos \gamma \cos \beta }&{\cos \gamma \sin \beta \sin \alpha - \sin \gamma \cos \alpha }&{\cos \gamma \sin \beta \cos \alpha + \sin \gamma \sin \alpha }\\ {\sin \gamma \cos \beta }&{\sin \gamma \sin \beta \sin \alpha + \cos \gamma \cos \alpha }&{\sin \gamma \sin \beta \cos \alpha - \cos \gamma \sin \alpha }\\ { - \sin \beta }&{cos\beta \sin \alpha }&{\cos \beta \cos \alpha } \end{array}} \right]. \end{array}$ |
|
图 1 抛物面天线变形示意 Figure 1 Schematic diagram of paraboloid antenna deformation |
利用最小二乘法对某一纵切面θ内变形后某时刻天线肋的采样点坐标值进行曲线拟合得到抛物线二次多项式f(ut, zt)=0,其对应的抛物线焦点pθ(lθ, zθ),其中ut2=xt2+yt2.对各纵切面对应的焦点求平均值,即可得到任一时刻抛物面天线的焦点值P为
| $P = (\frac{{\sum {l_\theta }\cos \theta }}{n},\frac{{\sum {l_\theta }\sin \theta }}{n},\frac{{\sum {z_\theta }}}{n}),$ | (2) |
式中,
可得到由于天线焦点位置变化引起的指向精度偏差为
| $\Delta \varphi = {\rm{arccos}}\left( {\frac{{{\mathit{\boldsymbol{r}}_1}{\mathit{\boldsymbol{r}}_2}}}{{\left| {{\mathit{\boldsymbol{r}}_1}} \right|\left| {{\mathit{\boldsymbol{r}}_2}} \right|}}} \right).$ | (3) |
式中,r1为方向矢量(0,0,1),r2为方向矢量
文献[15-17]建立口径12 m的径向肋式可展开抛物面天线的有限元模型,如图 2所示.当整星完全展开锁定后,部件之间的连接方式等效为刚性连接.采用多点约束将天线和太阳帆板与中心星体连接得到整星有限元模型.

|
图 2 整星有限元模型 Figure 2 Finite element model of the whole-spacecraft |
肋条采用Shell单元等效,肋间拉索采用Truss单元等效.天线质量约为350 kg,肋条材料采用碳纤维复合材料,拉索的横截面积为10 mm2.其预应力通过降温法获得,即
| $ - F = \alpha EA(T - {T_{{\rm{ref}}}}).$ | (4) |
式中:F为预应力; α为热膨胀系数; E为弹性模量; A为拉索横截面积; T、Tref分别为当前温度和参考温度.星载天线的其余物理参数见表 1,刚体质心在其几何中心.
| 表 1 星载天线机构物理参数 Table 1 Physical parameters of spaceborne antenna |
由于结构的对称性,相邻两阶模态的结构振型相似且固有频率值相近.由于预应力的存在改变了柔性天线面的刚度,会使天线面的固有频率值略有不同,但不影响天线的振动形式.增大温度载荷使拉索应力呈正比增加,拉索应力与截面面积的乘积增加,使得径向支撑肋的拉应力也增加.在拉索截面面积不变的条件下,拉索应力增加,拉索的等效抗弯刚度增加,径向支撑肋由于轴向拉力增大导致其等效抗弯刚度减小.对比不同预应力对应的固有频率值,可以发现,受径向支撑肋等效抗弯刚度降低的影响,7、8阶频率随拉索预应力的增加而略有降低;9阶及之后各阶频率在拉索等效刚度提高的影响下随拉索预应力的增加而逐渐增大.
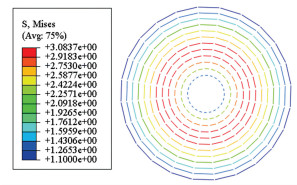
为对含预应力径向肋天线进行模态分析,首先对无应力有限元模型进行温度载荷作用下的非线性静力计算,得出天线径向肋间拉索的预应力分布;然后对含应力有限元模型进行模态分析,得到含预应力径向肋天线的振型与固有频率值.太空中的工况环境是浮动的,自由边界条件下有限元模型1~6阶模态为刚体模态.柔性天线前4阶固有频率为零,其中第1阶模态为天线绕z轴的旋转模态,第2阶~第4阶模态为天线的平移模态.第5阶和第6阶模态是以卫星质点为中心的刚体转动模态.第7阶~第12阶为天线肋条的振动模态.图 3为天线结构7~12阶模态振型云图,表 2为对应不同拉索预应力值的天线结构7~12阶固有频率值,表 2中给出的预应力对比值是天线拉索预应力的平均值.预紧力大小一般选择在拉索材料拉伸变形的弹性抗力范围内.预紧力太大会对展开结构的刚度提出过高的要求;预紧力太小会对型面精度的保持产生不良的影响.根据找形需求,预张力通过力密度法求出.本文选取预应力均值2.32 MPa和5.43 MPa为例分析对比不同预应力值对天线模态的影响.非线性静力分析的拉索应力分布如图 4所示,图 4显示的天线预应力分布对应平均预应力值为2.32 MPa的情况.

|
图 3 天线7~12阶模态振型云图 Figure 3 7-12 order vibration mode nephograms of antenna |
| 表 2 天线有限元模型固有频率 Table 2 Natural frequencies of antenna finite element model |
|
图 4 温度载荷下拉索应力分布 Figure 4 Cable stress distribution under temperature load |
挠性航天器的中心星体可看作刚体,挠性附件如展开天线和太阳帆板绕中心体作平动或转动的同时还伴随着自身结构振动.尤其是柔性反射面具有尺寸大、质量轻和柔性大等特点,星体调姿等大范围刚体运动会激起柔性反射面较大幅值的弹性振动,其振动产生的扰动又将影响星体调姿运动过程,这是典型的刚柔耦合动力学问题.
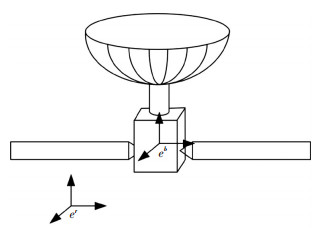
如图 5所示,er为惯性坐标系,eb为浮动坐标系,则航天器任意一点p在惯性坐标系下的位置向量r为
| $\mathit{\boldsymbol{r}} = {\mathit{\boldsymbol{r}}_0} + \mathit{\boldsymbol{A}}\left( {{\mathit{\boldsymbol{\rho }}_0} + {\mathit{\boldsymbol{u}}_0}} \right).$ | (5) |
|
图 5 抛物面天线航天器示意 Figure 5 Schematic diagram of satellite with paraboloid antenna |
式中:r0为eb坐标原点位置矢量;A为从er到eb的转换矩阵;ρ0为未变形构件上任一点p在eb中的位置矢量;up为变形矢量,用模态坐标表示为
| ${\mathit{\boldsymbol{u}}_p} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_p}{\mathit{\boldsymbol{q}}_f}.$ | (6) |
式中:Φp为点p的模态阵型矩阵,qf为广义位移.可得柔性体上任一点p的速度和加速度为
| $\mathit{\boldsymbol{\dot r}} = {{\mathit{\boldsymbol{\dot r}}}_0} + \mathit{\boldsymbol{\dot A}}\left( {{\mathit{\boldsymbol{\rho }}_p} + {\mathit{\boldsymbol{u}}_p}} \right) + \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_p}{{\mathit{\boldsymbol{\dot q}}}_f},$ | (7) |
| $\mathit{\boldsymbol{\ddot r}} = {{\mathit{\boldsymbol{\ddot r}}}_0} + \mathit{\boldsymbol{\ddot A}}\left( {{\mathit{\boldsymbol{\rho }}_p} + {\mathit{\boldsymbol{u}}_p}} \right) + 2\mathit{\boldsymbol{\dot A}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_p}{{\mathit{\boldsymbol{\dot q}}}_f} + \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_p}{{\mathit{\boldsymbol{\ddot q}}}_f}.$ | (8) |
考虑节点p变形前后位置、方向和模态,柔性体的广义坐标可以表示为
| $\mathit{\boldsymbol{\xi }} = {\left[ {x,y,z,\psi ,\varphi ,{q_i}\left( {i = 1,\cdot\cdot\cdot,m} \right)} \right]^{\rm{T}}} = {\left[ {r,\psi ,q} \right]^{\rm{T}}},$ | (9) |
式中m为模态数.
则速度可以表示为
| ${\mathit{\boldsymbol{v}}_0} = \left[ {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{A}}\left( {{\mathit{\boldsymbol{\rho }}_p}\tilde + {\mathit{\boldsymbol{u}}_p}} \right)\mathit{\boldsymbol{BA}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_p}} \right]\mathit{\boldsymbol{\dot \xi }},$ | (10) |
式中B为欧拉角的时间导数与角速度之间的转换矩阵.
运用拉格朗日乘子法建立柔性体的运动微分方程为
| $\mathit{\boldsymbol{M\ddot \xi }} + \mathit{\boldsymbol{M\dot \xi }} - \frac{1}{2}{[\frac{{\partial \mathit{\boldsymbol{M}}}}{{\partial \mathit{\boldsymbol{\xi }}}}\mathit{\boldsymbol{\dot \xi }}]^{\rm{T}}}\mathit{\boldsymbol{\dot \xi }} + \mathit{\boldsymbol{K\xi }} + \mathit{\boldsymbol{C\dot \xi }} + {[\frac{{\partial \mathit{\boldsymbol{\psi }}}}{{\partial \mathit{\boldsymbol{\xi }}}}]^{\rm{T}}}\mathit{\boldsymbol{\lambda }} = \mathit{\boldsymbol{Q}}.$ | (11) |
式中:M、K、C分别为结构的质量、刚度和阻尼矩阵;λ为拉格朗日乘子;Q为广义外力.
4 刚柔耦合动力学仿真挠性航天器在轨运行的动态响应求解属于刚柔耦合动力学问题.采用有限元与ADAMS联合仿真求解,建立整星零次刚柔耦合动力学模型,柔性部件上任意一点的运动等效为刚体位移和变形位移的叠加[18].本文取柔性部件除去刚体模态的前20阶模态构建动力学模型.ADAMS默认模型阻尼设置为固有频率在100 Hz以下的模态阻尼率为0.1%;固有频率在100~1 000 Hz的模态阻尼率为1%.考虑实际展开肋天线阻尼器分布的影响,本文阻尼比设置为0.004.仿真过程为采用3次样条规划,整星以角速度1.5 (°)/s作方位向调姿,整个调姿过程持续7.3 s,加、减速度过程各持续0.3 s,如图 6所示.仿真时间25 s,仿真步长0.01 s.

|
图 6 调姿角速度曲线 Figure 6 Angular velocity in attitude-adjusting process |
3次多项式规划角速度曲线函数如下:
| $\omega = \left\{ {\begin{array}{*{20}{l}} {1.5 \times \frac{{{t^2}}}{{{{0.3}^2}}} \times \left( {3 - 2 \times \frac{t}{{0.3}}} \right),0 \le t \le 0.3;}\\ {1.5,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0.3 \le t \le 7.0;}\\ {1.5 - 1.5 \times \frac{{{{\left( {t - 7} \right)}^2}}}{{{{0.3}^2}}} \times \left( {3 - 2 \times \frac{{t - 7}}{{0.3}}} \right),}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;7.0 \le t \le 7.3}\\ {0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;7.3 \le t \le 25.0.} \end{array}} \right.$ | (12) |
以下结果曲线均以天线预应力平均值为2.32 MPa情况为例求得.图 7为柔性天线结构边缘N点(图 2)的位移曲线.可以看出,挠性部件在做大范围整体运动的同时发生较显著的结构振动,当卫星完成调姿后,柔性天线结构继续在平衡位置处振动.

|
图 7 节点N在z方向的位移 Figure 7 Displacement of the node N along z direction |
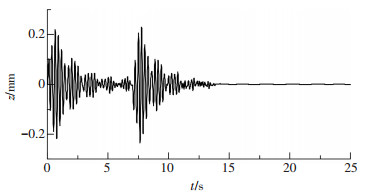
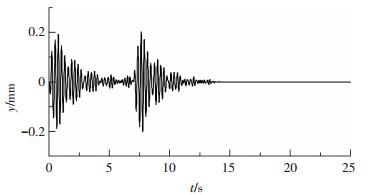
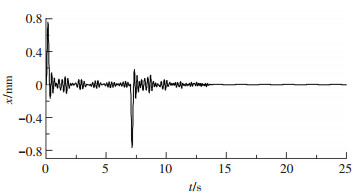
图 8~10分别为抛物面天线焦点在x,y,z方向的偏移量值随时间变化的曲线.由于做方位向调姿,所以其x向的振动量最大.可以看出,在速度发生改变的两时刻处即0~0.3 s和7.0~7.3 s,天线的视在相位中心产生较大偏移,尤其是x方向.调姿结束后天线焦点在平衡位置保持震荡,一段时间后渐趋于稳定.
|
图 8 焦点在x方向偏移量 Figure 8 Offset of the focus along x direction |
|
图 9 焦点在y方向偏移量 Figure 9 Offset of the focus along y direction |
|
图 10 焦点在z方向偏移量 Figure 10 Offset of the focus along z direction |
图 11为整个调姿过程中几何焦点相对于静态焦点位置的偏移情况.可以看出受焦点x向大幅震荡的影响,焦点在两加速度出现处发生较大的位置偏移,最大偏移量达到0.767 mm.其余时间,焦点震荡范围较集中,在±0.227 mm范围内.

|
图 11 天线几何焦点偏移量 Figure 11 Offset of the antenna focus |
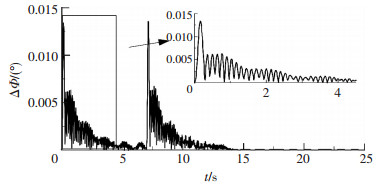
由于刚柔耦合作用,卫星自身的机械运动引起大型反射面天线的振动,从而严重影响天线的指向精度,使得卫星成像质量大幅降低.考虑天线柔性在刚柔耦合运动过程中对星载天线指向精度的影响,图 12显示了整个调姿过程中天线指向精度的变化曲线.可以看出,调姿过程中加速度的出现使得天线作较剧烈的振动,受x方向焦点大幅振动的影响,指向偏差的最大值出现在0~0.3 s和7.0~7.3 s,其值为0.013 5°.其余调姿过程中,指向精度偏差控制在0.006 4°以内.调姿结束后,指向偏差在一定时间范围内依然存在,随着时间的推移指向精度逐渐提高.
|
图 12 天线指向精度 Figure 12 Pointing accuracy of the antenna |
1)得出了一种在整星运行过程中确定其动态几何焦点的方法,可以检测天线焦点3个坐标值的偏移量,从而评估天线在运动过程中柔性面的振动对天线指向精度的影响.
2)通过改变径向肋天线的刚度和强度,调整天线的预张力可以在较小范围内改变天线面的固有频率,但取值合理且分布均匀的预张力的大小不影响天线面的振动形式.
3)挠性附件的结构振动在调姿运动结束后会保持一段时间才渐趋于稳定,抛物面天线焦点在一定范围内震荡造成相位中心的抖动,严重影响天线的稳定性和指向精度, 且几何焦点的偏移量与姿态调整的运动方向相关.
| [1] |
刘明治, 高桂芳. 空间可展开天线结构研究进展[J].
宇航学报, 2003, 24 (1) : 82-87.
LIU Mingzhi, GAO Guifang. Advances in the study on structure for space deployable antenna[J]. Journal of Astronautics, 2003, 24 (1) : 82-87. DOI: 10.3321/j.issn:1000-1328.2003.01.016 |
| [2] | THEUNISSEN W H, YOON H T, BURNSIDE W D, et al. Reconfigurable contour beam-reflectorantenna synthesis using amechanical finite-element description of the adjustable surface[J]. IEEE Transactions on Antennas and Propagation, 2001, 49 (2) : 272-279. DOI: 10.1109/8.914294 |
| [3] |
蒋尔进. 一种圆抛物面天线的有限元分析[J].
雷达与对抗, 2004 (4) : 61-64.
JIANG Erjin. Finite element analysis of a circular parabolic antenna[J]. Radar & Ecm, 2004 (4) : 61-64. |
| [4] | SREEKANTAMURTHY T, GASPAR J L, MANN T, et al. Nonlinear structural analysis methodology and dynamics scaling of inflatable parabolic reflector antenna concepts[C]//Proceeding of the 48th AIAA/ASME/ ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Honolulu, Hawaii: AIAA, 2007: 1-15.DOI: 10.2514/6.2007-1834. |
| [5] | MOBREM M, KUEHN S, SPIER C, et al. Design and performance of Astromesh reflector onboard Soil Moisture Active Passive spacecraft[C]//Aerospace Conference, 2012 IEEE. Piscataway: IEEE, 2012:1-10. DOI: 10.1109/AERO.2012.6187094. |
| [6] | DATASHVILI L, ENDLER S, WEI B, et al. Study of mechanical architectures of large deployable space antenna apertures: from design to tests[J]. CEAS Space Journal, 2013, 5 (3) : 169-184. DOI: 10.1007/s12567-013-0050-9 |
| [7] | GIUDICI D, DARIA D, GUARNIERI A M, et al. Analysis of antenna pointing errors on sar image quality[J]. IEEE Radar Conference, 2008, 1 : 1506-1511. DOI: 10.1109/RADAR.2008.4721087 |
| [8] | GAWRONSKI W, BANER F, QUINTERO O. Azimuth-track level compensation to reduce blind-pointing errors of the deep space network antennas[J]. IEEE Antenna and Propagation Magazine, 2000, 42 (2) : 28-38. DOI: 10.1109/74.842123 |
| [9] |
潘博, 张东华, 史文华, 等. 星载天线指向精度建模与分析[J].
航天器工程, 2011, 20 (5) : 49-54.
PAN Bo, ZHANG Donghua, SHI Wenhua, et al. Modeling and analysis on pointing accuracy of antenna in satellite[J]. Spacecraft Engineering, 2011, 20 (5) : 49-54. DOI: 10.3969/j.issn.1673-8748.2011.05.011 |
| [10] |
游斌弟, 赵阳, 赵志刚, 等. 柔性关节动态误差对星载天线扰动及控制[J].
机械工程学报, 2011, 47 (5) : 85-92.
YOU Bindi, ZHAO Yang, ZHAO Zhigang, et al. Disturbance on satellite antenna by dynamic error of flexible-joint and trajectory tracking control[J]. Journal of Mechanical Engineering, 2011, 47 (5) : 85-92. DOI: 10.3901/JME.2011.05.085 |
| [11] |
游斌弟, 赵志刚, 李文博, 等. 空间热载荷作用下星载天线耦合动态影响分析[J].
振动与冲击, 2012, 31 (17) : 61-66.
YOU Bindi, ZHAO Zhigang, LI Wenbo, et al. Coupling dynamic performance analysis for a satellite antenna system with space thermal load[J]. Journal of Vibration and Shock, 2012, 31 (17) : 61-66. |
| [12] | BAI Zhengfeng, TIAN Hao, ZHAO Yang. Dynamics modeling and simulation of mechanism with joint clearance[J]. [S.l.]: Journal of Harbin Institute of Technology, 2010, 17 (5) : 706-710. |
| [13] | BALANIS C A. Antenna theory: analysis and design[M]. 2016 : 837 -846. |
| [14] |
汪泉弟, 罗宏伟. 旋转抛物面天线馈源相位中心的仿真分析[J].
重庆大学学报, 2013, 36 (4) : 45-50.
WANG Quandi, LUO Hongwei. The simulation and research on feed's phase center of rotating parabolic antennas[J]. Journal of Chongqing University (Natural Science Edition), 2013, 36 (4) : 45-50. |
| [15] | STERBINI G. Analysis of satellite multibeam antennas's performances[J]. Acta Austronautica, 2006, 59 (1/2/3/4/5) : 166-174. DOI: 10.1016/j.actaastro.2006.02.027 |
| [16] | TIBERT G. Deployable tensegrity structures for space applications[M]. Stockholm: Royal Institute of Technology, 2002 : 17 -22. |
| [17] | 陈赓超.网状可展开天线力学分析研究[D].西安:西安电子科技大学, 2007: 33-64. |
| [18] |
张巍耀, 高晶波, 王聪. 大型挠性航天器刚柔耦合动特性分析[J].
哈尔滨工业大学学报, 2015, 47 (5) : 46-49.
ZHANG Weiyao, GAO Jingbo, WANG Cong. Rigid-flexiblecoupling dynamic analysis of the spacecraft installing large flexible attachments[J]. Journal of Harbin Institute of Technology, 2015, 47 (5) : 46-49. DOI: 10.11918/j.issn.0367-6234.2015.05.008 |
 2017, Vol. 49
2017, Vol. 49


