常规超声波检测过程中,需在待检测材料表面涂抹水或油等液体耦合剂,而对于固体火箭发动机(solid rocket motor,SRM)壳体粘接结构,若涂抹耦合剂会造成沾染,且不易清除,长期使用会影响材料的物理和化学性能,性能一旦下降就会影响结构的完整性,从而造成难以估量的后果,因此迫切需要寻求一种无需耦合剂的超声检测方法,而干耦合法由于探头和试件直接接触,不需其他耦合介质,检测手段灵活,可用于外场检测,适用于对SRM壳体材料的检测.
时间反转聚焦理论最早由法国科学家Fink等[1-2]由光学引入到声学领域,它通过将响应信号在时域内进行反转,二次激发,使其在波源处实现时-空上的聚焦.提取聚焦后信号中特征值,结合椭圆等定位技术,将表征值分布与图像中各个像素点的对比度关联起来,从而得到缺陷的图像.目前,国外对于时间反转方法的研究比较深入,美国南卡罗来纳大学Giurgiutiu等[3]从理论和实验两方面对导波的时间反转聚焦原理、过程进行了研究,表明时间反转方法对于复杂结构的检测成像有较好研究前景.Sohn等[4]对如何增强复合材料中导波的时反特性进行研究,重构了激励源发射信号,并进行缺陷特征评价.英国巴斯大学Erik等[5]从数学的角度提出了源时间反转方法,与传统的全时间反转方法进行了对比分析,并将其应用于混凝土试件的声发射检测过程中.国内,屈文忠等[6-7]运用导波时间反转方法对铝板进行了损伤识别定位实验,结果表明距离比较分开且具有相对不同损伤程度的2处损伤,导波时间反转分解方法能够有效识别并准确定位.王强等[8-10]运用导波时间反转方法对环氧玻璃纤维板进行了损伤识别定位研究,运用四点圆弧定位法计算得到聚焦时刻,并用有限元的方法对试件划分网格,建立聚焦时刻的瞬态波动图从而绘出图像.周进节[11]基于时间反转方法研究了采用管道端面加载方式实现导波能量在缺陷处进行时间-空间聚焦的原理,在此基础上提出了斜入射局部加载及基于压电晶片阵列实现管中对缺陷两种时反检测方法.蔡建等[12]研究了一种基于宽带激励的虚拟时间反转方法,可提高损伤波包的空间分辨率,改进复杂结构中相邻缺陷成像质量.苗晓婷等[13]结合时间逆转的导波与加权分布成像算法对板中多个损伤进行检测,结果表明该方法不依赖基准信号,可精确定位铝板中的多个缺陷.
总体来看,将时间反转方法应用于复合材料的成像检测取得了良好效果,但是目前在检测中主要采取在材料表面粘贴固定压电晶片的方式进行,这种方式耗时较长,操作复杂,灵活性较差,不利于在外场进行操作,而本文研制的干耦合探头体积小、质量轻、接线方便、移动灵活,在此基础上开发了超声波干耦合检测系统,结合时间反转方法,对SRM壳体粘接结构试件中缺陷进行成像.
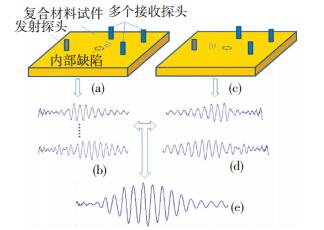
1 干耦合超声的时间反转方法干耦合超声时间反转聚焦的过程如图 1所示,首先,干耦合发射探头中压电振子受逆压电效应影响激发产生超声波,并通过传声杆传入到复合材料试件中;然后,多个干耦合接收探头在试件上不同位置接收板中的缺陷散射信号;其次,对接收信号进行时间反转、放大及延时等处理,并以原接收探头作为发射探头,将处理后的信号重新加载发射;最后,二次采集接收信号,信号在波源处产生聚焦放大效果.
|
图 1 干耦合超声时间反转过程 Figure 1 Time reversal process of dry-coupled ultraso |
假设发射探头产生的激励信号传播至板上任意点m处信号为em(t),那么接收探头接收到信号为
| $ {f_m}\left( t \right) = {h_m}\left( t \right) \otimes {e_m}\left( t \right) = \int_{ - \infty }^\infty {{h_m}\left( \tau \right){e_m}\left( {t - \tau } \right)d\tau } . $ | (1) |
式中:⊗为卷积,hm(t)为脉冲响应函数.从频域上式(1)可写为
| $ {F_m}\left( \omega \right) = {H_m}\left( \omega \right){E_m}\left( \omega \right). $ |
根据空间互异性原理,如
| $ {E_m}\left( \omega \right) = H_m^{\rm{T}}\left( \omega \right){F_m}\left( \omega \right). $ | (2) |
假设缺陷位置为m0,那么接收信号为
| $ {F_{m0}}\left( \omega \right) = {H_{m0}}\left( \omega \right){E_{m0}}\left( \omega \right). $ | (3) |
信号在时域上的时间反转过程等效于频域上信号经傅里叶变换后复数的共轭,因此式(3)可写为
| $ F_{m0}^*\left( \omega \right) = H_{m0}^*\left( \omega \right)E_{m0}^*\left( \omega \right) = H_{m0}^*\left( \omega \right){E_{m0}}\left( \omega \right), $ | (4) |
式中,*表示共轭.联合式(2)和式(4),m点的回波信号可写为
| $ \begin{array}{l} {E_{TR}}\left( \omega \right) = H_m^{\rm{T}}F_{m0}^*\left( \omega \right) = H_{m0}^*\left( \omega \right)E_{m0}^*\left( \omega \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;H_m^{\rm{T}}\left( \omega \right)H_{m0}^*\left( \omega \right){E_{m0}}\left( \omega \right). \end{array} $ | (5) |
当m=m0时,式(5)存在最大值.将式(2)两边同乘以Hm0*(ω),得到:
| $ \begin{array}{l} H_{m0}^*\left( \omega \right){E_m}\left( \omega \right) = H_{m0}^*\left( \omega \right)H_m^{\rm{T}}\left( \omega \right){F_{m0}}\left( \omega \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {{H_{m0}}{{\left( \omega \right)}^2}} \right|{F_{m0}}\left( \omega \right), \end{array} $ |
那么
| $ {F_{m0}}\left( \omega \right) = {{\tilde H}_{m0}}\left( \omega \right){E_{m0}}\left( \omega \right). $ |
式中,
| $ {E_{TR}}\left( \omega \right) = H_m^{\rm{T}}{F_{m0}}\left( \omega \right) = H_m^{\rm{T}}\left( \omega \right){{\tilde H}_{m0}}\left( \omega \right){E_{m0}}\left( \omega \right). $ | (6) |
运用时间反转方法进行缺陷定位原理图如图 2所示,当任意点m与缺陷点m0重合,即m=m0时,式(6)同样存在最大值.

|
图 2 运用时间反转方法进行缺陷定位原理 Figure 2 Defect localization principle by time reversal method |
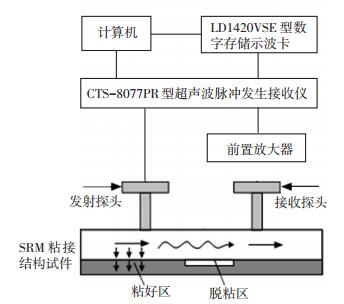
干耦合超声检测系统主要由干耦合探头、超声波脉冲发生接收仪、前置放大器、数字存储示波卡、探头工装、PC机以及编译的检测软件组成,工作原理如图 3所示,实物图如图 4所示.首先由超声波脉冲发生接收仪激励产生一定频率的脉冲信号,并将其加载在干耦合探头中压电振子上,受逆压电效应影响产生超声波,并以导波形式在板中传播,被接收探头接收后受压电效应影响超声波又转换为电信号,电信号经前置放大器放大后由数字存储示波卡进行采集、存储并通过PC机进行显示.
|
图 3 干耦合超声检测系统工作原理 Figure 3 The working principle of dry-coupled ultrasonic testing system |

|
图 4 干耦合超声检测系统 Figure 4 Dry-coupled ultrasonic testing system |
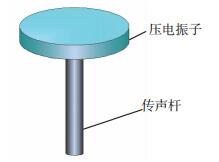
检测系统的核心部件为超声干耦合探头,每个干耦合探头可根据检测需要装载一个或多个子探头,其实物结构如图 5所示.传统的检测探头与试件之间多是通过耦合剂面接触的,这种方式超声波发射能量大,传递效率高;干耦合检测由于不允许使用耦合剂,为了保证足够的超声波入射能量,达到检测目的,必须设计特殊的结构形式.本文中,将干耦合探头设计成传声杆形式,结构示意图如图 6所示.压电振子上面与外部电路相连接,下部连接传声杆,为3层夹心结构,上下两层为两片沿厚度方向极化的压电陶瓷圆片,作为压电振子的驱动材料,中间一层为金属片,其直径略大于压电陶瓷圆片,用于支撑和进行电连接.传声杆采用透声性能较好的材料制成,而且比较细,只有压电振子直径的1/4,既能够将超声波能量进行聚焦,使超声波更加集中地传递到被检试件中.同时由于端面较小,与被检材料之间可近似认为是点接触,可克服传统检测由于空气的存在带来阻抗不匹配问题.

|
图 5 干耦合超声波探头 Figure 5 Dry-coupled ultrasonic probe |
|
图 6 传声杆结构示意 Figure 6 Transmission rod |
实验系统硬件主要包括:泰克AFG3052C型信号发生器、NF公司HSA4051型双极性功率放大器及RIGOL公司MSO1104型四通道示波器,硬件系统如图 7所示.

|
图 7 硬件系统 Figure 7 Hardware system |
影响时间反转操作的关键因素是超声波信号的激励与控制,根据大量试验结果及相关文献[14-15],本文采用5周期汉宁窗调制正弦函数作为激励信号,频率为70 kHz,信号重复频率为1 kHz, 电压峰峰值为2 V,输出阻抗为高阻600 Ω,功放倍数为20.检测时,首先由PC机调制激励信号,发送至信号发生器,设定好检测参数经功率放大后加载至发射探头,另在试件各检测位置布置接收探头与示波器相连,为保持各检测探头耦合压力一致,采用相同质量钢块进行加压.同时连接示波器与信号发生器的Trigger端使两者保持同步,并采用方波上升沿的方式进行触发控制.经USB通信后,在LabVIEW环境中可实现示波器各通道采集数据的同步显示与存储,将存储的信号数据进行截取、反转、放大等操作,并重新发送至信号发生器进行加载,交换发射/接收探头电缆,采集得到最终的聚焦放大信号,从而构成了整个时间反转操作这一闭环过程.
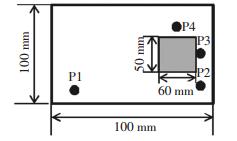
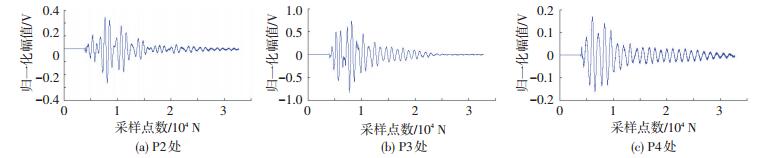
检测试件为钢壳体粘接结构,上层为30铬锰硅钢板, 用来模拟壳体,下层为三元乙丙橡胶配方,模拟绝热层,在钢和橡胶的粘接界面上预置了一个聚四氟乙烯薄膜模拟空气夹层脱粘缺陷,试件实物如图 8所示,结构尺寸如图 9所示,试件大小为180 mm×100 mm,壳体厚5 mm,绝热层厚3 mm,长方形区域为粘接界面上的脱粘缺陷,其大小为60 mm×50 mm.检测时,将发射探头置于坐标零点P1处,接收探头先后分别置于P2(145,0)、P3(145,40)、P4(105,80)处,检测区域为160 mm×80 mm的长方形区域,分别在P2、P3、P4处采集得到损伤散射信号,如图 10所示,从图 10中可以计算出导波到达损伤并被散射的时间td为0.1 ms,损伤散射信号被最后一个接收探头采集完毕的时刻tm为0.4 ms.

|
图 8 检测实物 Figure 8 Detection object |
|
图 9 结构尺寸 Figure 9 Structure size |
|
图 10 损伤散射信号 Figure 10 Damage scattering signals |
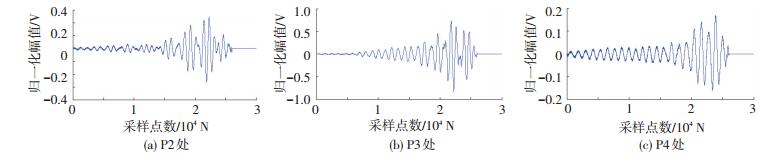
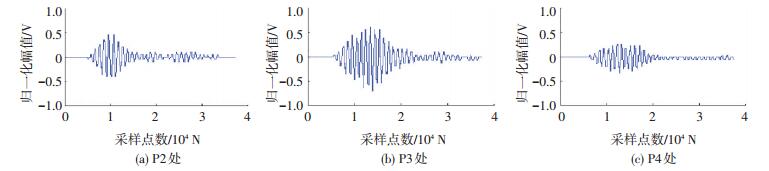
取tw=0.5 ms (必须大于tm),以tw为时间窗口,分别截取各损伤散射信号,并在时域内反转得到时反信号fn(n=1, 2, 3, …),如图 11所示.提取时反信号包络,首先将波形数据取绝对值,然后分成等宽度的小段,每段取一个最高点所对应的横坐标和纵坐标,宽度过大会导致信号变化的连续性较差,造成失真,宽度过小达不到提取目的,由于截取的数据长度为30 000,可以将宽度设为25,共1 200段,重新调整波形数据的行数、列数、维数,将每列中的最大值作为包络线的特征值,提取P2、P3、P4处时反后信号的包络如图 12所示,各位置处聚焦放大信号如图 13所示.建立聚焦时刻tf的瞬态波动图S,S中各像素点对应结构的一个微元,该时刻结构各单元的波动幅值可求得:
|
图 11 时反信号 Figure 11 Time reversal signals |

|
图 12 信号包络 Figure 12 Signal envelopes |
|
图 13 聚焦放大信号 Figure 13 Focus amplified signals |
| $ {S_{ij}} = \sum\limits_{n = 1}^N {{A_n}\cdot{f_n}({t_{ijn}}),} {t_{ijn}} = {t_f} - \frac{{\sqrt {{{(i \times f - {x_n})}^2} + {{(j \times f - {y_n})}^2}} }}{v}. $ |
式中:N为信号的个数;An为补偿第n个接收探头性能差异及监测信号能量衰减的放大系数,通常取归一化系数;v为声波在结构中的传播速度;f为图像像素点的分辨率;xn、yn分别为第n个传感器的坐标.各像素点的像素值还可以采用散射信号相乘的形式计算得出,如
| $ {S_{ij}} = \prod\limits_{n = 1}^N {{A_n}\cdot{f_n}({t_{ijn}}).} $ |
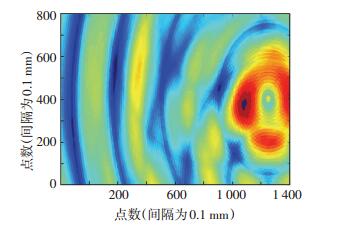
根据导波传播规律,聚焦时刻tf与到达损伤时间td之间的关系为:tf=tw-td=0.4 ms.取f=0.1 mm,超声波在钢中的传播速度为3 100 m/s,横坐标范围为0~160 mm,纵坐标范围为0~80 mm.根据求和、乘积形式得到最终的损伤成像分别如图 14、15所示.运用超声水浸C扫描得到的图像如图 16所示.
|
图 14 求和形式得到的损伤成像 Figure 14 Damage image by sum |
|
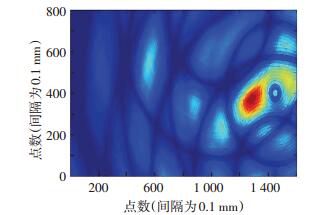
图 15 求积形式得到的损伤成像 Figure 15 Damage image by quadrature |

|
图 16 超声水浸C扫描图像 Figure 16 Ultrasonic C-scan image by immersion method |
从图 14, 15中可知,两种方法均能完整地将检测区域呈现出来,形状大小相同.从图 14中可以看出导波能量较大区域集中在横坐标为100~160 mm,纵坐标为20~70 mm范围内,从图 15中可以基本看出损伤的中心位置,约为(130 mm,40 mm),这均与试件中预置缺陷的位置及大小相符,结果是可信的.同时可以看出,对于以上两种形式定义的成像参数各有优点,求和形式算法对于多个损伤共存,或者大面积损伤有较好地反映,但是成像结果中存在一些虚假损伤;求积形式算法可以准确定位损伤引起散射点的位置,但是较难反映连续的散射区域.与常规的超声C扫描检测图像相比,虽然精度和准确度稍差,但干耦合成像检测克服了超声波需要耦合介质的问题.
5 结论1)设计了特别结构形式的压电振子及传声杆,构建了干耦合检测系统,检测时既不需要涂抹耦合剂,同时也保证了较大的超声波入射能量.
2)干耦合检测信号经过时间反转、二次加载及发射后会产生聚焦放大效果,位于缺陷处的能量最大.
3)通过对损伤散射信号进行采集、时间反转及提取包络线,建立信号聚焦时刻的瞬态波动图,根据实验数据初步验证了干耦合的时间反转成像检测方法.
| [1] | FINK M. Time reversed acoustics[J]. Physics Today, 1997, 50 (3) : 34-40. DOI: 10.1063/1.881692 |
| [2] | ING R K, FINK M. Time-reversed Lamb waves[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 1998, 45 (4) : 1032-1043. DOI: 10.1109/58.710586 |
| [3] | XU Buli, GIURGIUTIU V. Single mode tuning effects on lamb wave time reversal with piezoelectric wafer active sensors for structural health monitoring[J]. Journal of Nondestructive Evaluation, 2007, 26 (2) : 123-134. DOI: 10.1007/S10921-007-0027-8 |
| [4] | SOHN H, PARK H W, LAW K H, et al. Damage detection in composite plates by using an enhanced time reversal method[J]. Journal of Aerospace Engin-eering, 2007, 20 (3) : 141-151. DOI: 10.1061/(ASCE)0893-1321(2007)20:3(141) |
| [5] | SAENGER E H, KOCUR G K, JUD R, et al. Application of time reverse modeling on ultrasonic non-destructive testing of concrete[J]. Applied Mathematical Modeling, 2011, 35 (2) : 807-816. DOI: 10.1016/j.apm.2010.07.035 |
| [6] |
屈文忠, 肖黎. Lamb波时间反转分解损伤识别方法研究[J].
机械强度, 2014, 36 (1) : 7-10.
QU Wenzhong, XIAO Li. Time reversal decomposition based lamb wave damage detection method[J]. Journal of Mechanical Strength, 2014, 36 (1) : 7-10. DOI: 10.16579/j.issn.1001.9669.2014.01.006 |
| [7] |
冯继航, 屈文忠, 肖黎. 压电材料兰姆波方法在薄板损伤检测中的数值仿真[J].
武汉大学学报(工学版), 2010, 43 (4) : 519-522.
FENG Jihang, QU Wenzhong, XIAO Li. Numerical simulation of piezoelectric sensor Lamb wave method for plate damage detection[J]. Engineering Journal of Wuhan University, 2010, 43 (4) : 519-522. |
| [8] |
王强. Lamb波时间反转方法及其在结构健康监测中的应用研究[D].南京:南京航空航天大学, 2009.
WANG Qiang. Research on lamb wave time reversal technique and its applications in structural health monitoring[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009. |
| [9] |
王强, 严夏君, 陈小惠, 等. 无基准Lamb波时间反转损伤概率成像监测方法[J].
仪器仪表学报, 2013, 34 (7) : 1588-1593.
WANG Qiang, YAN Xiajun, CHEN Xiaohui, et al. Baseline free Lamb wave damage probability imaging monitoring method based on time reversal theory[J]. Chinese Journal of Scientific Instrument, 2013, 34 (7) : 1588-1593. DOI: 10.3969/j.issn.0254-3087.2013.07.022 |
| [10] |
王强, 袁慎芳, 邱雷, 等. 基于时间反转理论的结构损伤图像表征方法[J].
仪器仪表学报, 2008, 29 (9) : 1816-1821.
WANG Qiang, YUAN Shenfang, QIU Lei, et al. Image representation based on time reversal theory for structure health monitoring[J]. Chinese Journal of Scientific Instrument, 2008, 29 (9) : 1816-1821. DOI: 10.3321/j.issn:0254-3087.2008.09.005 |
| [11] |
周进节.基于时间反转方法的超声导波检测设备研制及其应用研究[D].北京:北京工业大学, 2012.
ZHOU Jinjie. Development and application of guided wave inspection device based on time reversal method[D]. Beijing: Beijing University of Technology, 2012. |
| [12] |
蔡建, 石立华, 袁慎芳, 等. 一种基于宽带激励的虚拟时间反转方法[J].
仪器仪表学报, 2011, 32 (1) : 218-224.
CAI Jian, SHI Lihua, YUAN Shenfang, et al. Virtual time reversal method based on broadband excitation[J]. Chinese Journal of Scientific Instrument, 2011, 32 (1) : 218-224. |
| [13] |
苗晓婷, 李富才, 孟光. 结合时间逆转的兰姆波与加权分布成像算法对多损伤识别的研究[J].
机械工程学报, 2011, 47 (16) : 1-8.
MIAO Xiaoting, LI Fucai, MENG Guang. Identification of multi-defects by combining time-reversal lamb waves with weight distribution imaging algorithm[J]. Journal of Mechanical Engineering, 2011, 47 (16) : 1-8. DOI: 10.3901/JME.2011.16.001 |
| [14] |
魏勤, 骆英, 王自平, 等. Lamb波驱动器的最佳激励波形选择[J].
压电与声光, 2011, 33 (6) : 863-866.
WEI Qin, LUO Ying, WANG Ziping, et al. Optimal excitation waveform selection for Lamb wave actuator[J]. Piezoelectrics & Acoustooptics, 2011, 33 (6) : 863-866. DOI: 10.3969/j.issn.1004-2474.2011.06.005 |
| [15] |
杨星.基于超声激励的频率跟踪技术[D].西安:陕西师范大学, 2013.
YANG Xing. Frequency automatic tracking technology base on ultrasonic irradiation[D]. Xi'an: Shanxi Normal University, 2013. |
 2017, Vol. 49
2017, Vol. 49


