2. 福州大学 爆炸技术研究所,福州350116;
3. 福州大学 环境与资源学院,福州350116;
4. 华中科技大学 土木工程与力学学院,武汉430074
2. Institute for Explosive Technology, Fuzhou University, Fuzhou 350116, China;
3. College of Environment and Resources, Fuzhou University, Fuzhou 350116, China;
4. School of Civil Engineering and Mechanics, Huazhong University of Science and Technology, Wuhan 430074, China
合理的微差爆破延期时间能改善爆破效果、降低成本[1].因此,众多学者对基于岩石破碎机理的微差爆破延时控制进行了研究.陈士海等[2]指出,起爆过程中先爆药包为后爆药包提供补充自由面,使得岩体裂隙侧边受到巨大的水平压力,建议此时起爆后爆药包,爆后效果最佳;Yamamoto等[3]指出爆破过程中岩体位移与抵抗线成函数关系,并给出每米抵抗线需时间5~7 ms;Mogi等[4]提出先爆药包应力波传到后爆药包,在应力波作用的同时起爆后爆药包,此时两者振动波存在时差以及速度差,岩块相遇时会产生相互碰撞形成补充破坏,爆破效果最佳,并给出最佳延期时间为15~50 ms;李洪涛等[5]通过研究等效峰值能量对建筑物爆破振动影响,指出峰值速度可作为最佳延期时间判断指标;凌同华等[6]通过小波变换时能密度分析,将波段分层重构和分辨分解来探究最佳延时控制;Lu等[7]通过研究爆破过程中振动波引起岩体质点模型结构响应规律,探究最佳延期时间.
爆破振动波信号属于离散型随机不稳定元素,利用振动波能量、频谱等作为载体研究微差爆破延时控制存在诸多不便和不准确性;再者,国内外基于岩石破碎机理研究微差爆破延时控制虽给出了半理论、半经验公式,但该成果多以炸药爆炸过程中释放的某一主要能量作用方式为主(应力波或者爆生气体),缺乏全面性和科学性.爆破破岩过程是应力波和爆生气体二者综合作用结果,本文从爆破机理理论出发,以爆炸过程能量综合作用方式和破坏形式为基础,采用理论号实验相结合的方法,对理论推导模型进行实验验证,探究最佳延期控制时间.
1 多形式爆炸能释放理论模型的确定在应力波和爆生气体综合作用破坏过程中,应力波主要以动力破坏形式为主,而爆生气体则为准静态破坏.起爆过程中应力波使岩体产生裂纹裂隙,将原始损伤扩大加剧裂隙扩展;随之爆生气体渗入裂隙,进一步贯穿,扩大破坏范围,导致岩块脱离母岩.
1.1 应力波作用数学模型 1.1.1 应力波运动方程药包起爆后,应力波首先对炮孔产生破坏,进入径向压缩阶段.应力波的高压高能使围岩粉碎,催使岩石裂纹裂隙扩展,形成粉碎区,其运动方程可以直接从变形状态方程导出[8].
| $ \frac{1}{{{c^2}}}\frac{{{\partial ^2}u}}{{\partial {t^2}}} = \frac{{{\partial ^2}u}}{{\partial {\gamma ^2}}} + \frac{1}{r}\frac{{\partial u}}{{\partial r}} - \frac{u}{{{\gamma ^2}}}. $ | (1) |
式中:c为弹性纵波的传播速度,
以逐孔微差爆破为例,假设炮孔中心为O、半径为r,则位移u是时间t′的函数方程.其中
| $ u\left( {r,t} \right) = v\left[ {r,t - \frac{{r - R}}{C}} \right]. $ |
令
| $ \begin{array}{l} \frac{{{\partial ^2}u}}{{\partial {t^2}}} + \frac{1}{r}\frac{{\partial u}}{{\partial t}} - \frac{u}{{{\gamma ^2}}} = \frac{{{\partial ^2}\left[ v \right]}}{{\partial {r^2}}} - \frac{2}{c}\frac{{{\partial ^2}\left[ v \right]}}{{\partial r\partial t'}} + \frac{1}{{{c^2}}}\frac{{{\partial ^2}\left[ v \right]}}{{\partial {{t'}^2}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{r}\left[ {\frac{{\partial \left[ v \right]}}{{\partial r}} - \frac{1}{{{c^2}}}\frac{{\partial \left[ v \right]}}{{\partial t'}}} \right] - \frac{{\left[ v \right]}}{{{r^2}}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{{{c^2}}}\frac{{{\partial ^2}\left[ v \right]}}{{\partial {{t'}^2}}} - \frac{2}{c}\frac{{{\partial ^2}\left[ v \right]}}{{\partial r\partial t'}} + \frac{1}{r}\frac{{\partial \left[ v \right]}}{{\partial r}} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{{rc}}\frac{{\partial \left[ v \right]}}{{\partial t'}} - \frac{{\left[ v \right]}}{{{r^2}}}, \end{array} $ | (2) |
而波动方程又适合于[v],故
| $ \frac{\partial }{{\partial r}} \cdot \frac{1}{r}\frac{{\partial \left( {u,r} \right)}}{{\partial r}} = - \frac{1}{{rc}}\frac{\partial }{{\partial r}}\left( {r,\frac{{\partial \left[ v \right]}}{{\partial t'}}} \right) + \frac{1}{{rc}}\frac{{\partial \left[ v \right]}}{{\partial t'}}. $ | (3) |
将式(3)对孔内任意位置积分可得:
| $ \begin{array}{l} \int_R^r {\frac{\partial }{{\partial r}}} \cdot \frac{1}{r}\frac{{\partial \left( {u,r} \right)}}{{\partial r}}{\rm{d}}r = \frac{1}{r}\frac{{\partial \left( {u,r} \right)}}{{\partial r}} - {\left[ {\frac{1}{r}\frac{{\partial \left( {u,r} \right)}}{{\partial r}}} \right]_R} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{r}\frac{{\partial \left( {u,r} \right)}}{{\partial r}} - \frac{{{u_R}}}{R} + {\left( {\frac{{\partial u}}{{\partial r}}} \right)_{r = R'}}. \end{array} $ | (4) |
| $ \begin{array}{l} - \frac{2}{c}\int_R^r {\frac{1}{r}} \frac{\partial }{{\partial r}}\left( {r,\frac{{\partial \left[ v \right]}}{{\partial t'}}} \right){\rm{d}}r = - \frac{2}{c}\left[ {{{\left( {\frac{{\partial \left[ v \right]}}{{\partial t'}}} \right)}_r} - {{\left( {\frac{{\partial \left[ v \right]}}{{\partial t'}}} \right)}_R}} \right] - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{2}{c}\int_R^r {\frac{1}{r}} \frac{{\partial \left[ v \right]}}{{\partial t'}}{\rm{d}}r{\rm{ = }}\frac{2}{c}{\left( {\frac{{\partial \left[ v \right]}}{{\partial t'}}} \right)_R} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{2}{c}\int_R^r {\frac{1}{r}} \frac{{\partial \left[ v \right]}}{{\partial t'}}{\rm{d}}r, \end{array} $ | (5) |
|
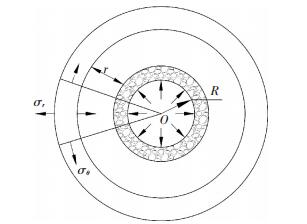
图 1 炮孔受力 Figure 1 Free body diagram of blasthole |
在时间
| $ \begin{array}{l} {u_r} = R \cdot {u_R} + \left[ {\frac{{{u_R}}}{R} + {{\left( {\frac{{\partial u}}{{\partial t}}} \right)}_R} + {{\left( {\frac{{\partial \left[ v \right]}}{{\partial t'}}} \right)}_R}} \right] \cdot \frac{{{r^2} - {R^2}}}{2} - \\ \;\;\;\;\;\;\frac{1}{c}\int_R^r {r{\rm{d}}r} \int_R^r {\frac{1}{\xi }} \frac{{\partial \left[ v \right]}}{{\partial t'}}{\rm{d}}\xi {\rm{.}} \end{array} $ | (6) |
爆破为动力学过程,故式(6)静力平衡可省去,而孔内扰动位移项极小,也可忽略.即整个应力波作用过程岩石位移只取决于时间先于(r-R/c)的速度
| $ u\left( {r,t} \right) = \frac{1}{c}{\left( {\frac{{\partial \left[ v \right]}}{{\partial t'}}} \right)_R} \cdot \left[ {\left( {{r^2} - {R^2}} \right)/2} \right]. $ | (7) |
假设在弹性范围内研究应力波破岩,可用Hooke定律并结合式(7)求解动应力方程[9]:
| $ \left\{ \begin{array}{l} {\sigma _r} = \frac{E}{{c\left( {1 + \gamma } \right)\left( {1 - 2\gamma } \right)}}{\left[ {\frac{{\partial \left[ v \right]}}{{\partial t'}}} \right]_R}\left[ {1 + \left( {1 - 2\gamma } \right)\frac{{{R^2}}}{{{r^2}}}} \right],\\ {\sigma _\theta } = \frac{E}{{c\left( {1 + \gamma } \right)\left( {1 - 2\gamma } \right)}}{\left[ {\frac{{\partial \left[ v \right]}}{{\partial t'}}} \right]_R}\left[ {1 - \left( {1 - 2\gamma } \right)\frac{{{R^2}}}{{{r^2}}}} \right]. \end{array} \right. $ | (8) |
式中:σr为径向动应力, σθ为切向动应力.
应力波作用过程中动态剪应力可由式(8)求得:
| $ \tau = \frac{{{\sigma _r} - {\sigma _\theta }}}{2} = \frac{E}{{c\left( {1 + \gamma } \right)}}\frac{{{R^2}}}{{{r^2}}}{\left( {\frac{{\partial \left[ v \right]}}{{\partial t'}}} \right)_R}, $ | (9) |
由式(9)可知,当r=R时动态剪应力最大,即孔壁处最大,取最大值为τmax, 即
| $ {\tau _{\max }} = \frac{E}{{c\left( {1 + \gamma } \right)}}{\left( {\frac{{\partial \left[ v \right]}}{{\partial t'}}} \right)_R}. $ | (10) |
炸药爆炸后,孔壁岩石质点产生位移并传递给相邻质点,质点产生的径向位移和环向位移导致外岩层出现切向和经向应变;在爆炸载荷作用下,炮孔岩层质点受到向外冲量,使得σr变为拉应力.岩石抗压强度远远大于抗拉强度,使岩块产生径向和环向裂隙;
为研究方便,同样选取逐孔微差爆破为对象,假设爆破过程中应力波产生的破坏区域半径为A,根据岩体强度破坏准则可知,若破坏为径向动拉应力破坏,破坏条件为
| $ {\left( \sigma \right)_{\max }} = \left[ {{\sigma _b}} \right], $ | (11) |
式中, [σb]为岩石的单轴抗拉强度.
将式(8)代入式(11)可得:
| $ A = R\sqrt {\frac{{\left( {1 - 2\gamma } \right)c\rho {{\left( {\frac{{\partial \left[ v \right]}}{{\partial t'}}} \right)}_R}}}{{\left( {1 - \gamma } \right) - c\rho {{\left( {\frac{{\partial \left[ v \right]}}{{\partial t'}}} \right)}_R}}}} , $ | (12) |
同样,若应力波破坏为切向动应力破坏,破坏条件为
| $ {\tau _{\max }} = \left[ {{\tau _b}} \right], $ | (13) |
式中, [τb]为岩石的抗剪切强度.
将式(8)代入式(13)可得:
| $ A = R\sqrt {\frac{{\left( {1 - 2\gamma } \right)c\rho {{\left( {\frac{{\partial \left[ v \right]}}{{\partial t'}}} \right)}_R}}}{{\left( {1 - \gamma } \right)\left[ {{\sigma _b}} \right]}}} . $ | (14) |
应力波作用产生粉碎和裂隙的同时,爆生气体膨胀产生准静态应力场,加大裂隙区破坏范围.爆生气体膨胀过程时间极短,可假设是一种等熵绝热过程[10],则爆生气体在裂隙中的压力表示为
| $ {p_0} = {p_k}{\left( {\frac{{{p_\omega }}}{{{p_k}}}} \right)^{\gamma /k}}{\left( {\frac{{{r_c}}}{r}} \right)^{2\gamma }}. $ | (15) |
式中: pk为临界压力;γ为绝热指数,k为等熵指数(通常取γ=1.4,k=3);pω为平均压力,pω=ρ0D2/2(1+k),D为爆速; ρ0为炸药密度;r为炮孔直径;rc为装药半径.
由热力学知识中气体等熵膨胀理论可得出爆生气体膨胀随时间变化的压力表达式为
| $ p\left( t \right) = \frac{{{p_0}}}{\varepsilon }{\left( {1 + \frac{x}{{{C_0}t}}} \right)^k}. $ | (16) |
式中:x为爆生气体运动范围,0≤x≤Lb,其中Lb为炮孔长度;
爆生气体从开始到破坏整个过程中膨胀时间可由式(16)得到:t=Lb/C0(81/k-1).由于爆生气体对炮孔破坏为扩腔和致裂,而扩腔主要是对炮孔的纵向破坏,所以研究爆生气体破坏范围只考虑致裂作用.假设爆生气体作用过程中炮孔壁不动,则爆生气体膨胀压力为
| $ p = {p_0}\left( {\frac{{{\rm{\pi }}{r^2}}}{{{\rm{\pi }}{r^2} + 2\alpha b}}} \right)\gamma , $ | (17) |
式中: b为裂隙宽度,α为裂隙长度.
故由式(16),可将膨胀压力随时间变化表示为
| $ p\left( t \right) = {p_0}{\left( {\frac{Z}{{{C_0}t - H}}} \right)^\alpha }. $ | (18) |
逐孔爆破中,取γ=1.4,α=1.55;Z、H分别为常数,Z=0.27Lb,H=0.83Lb.
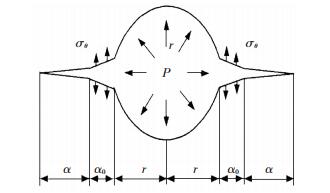
1.2.2 爆生气体破岩条件逐孔爆破中爆生气体进入裂隙时,由应力集中原理说明两相邻炮孔在直线方向所产生的破坏力最大,为研究方便,只考虑直线方向破坏.由断裂力学理论,裂隙端部强度因子只要大于岩层裂隙层面的断裂韧性,将开始破坏(见图 2, 3),引起裂隙的进一步扩展[3].图 2中,α0表示应力波作用下产生的裂隙长度,α表示爆生气体作用下拓展的裂隙长度.
|
图 2 断裂力学模型 Figure 2 The fracture mechanics pattern |
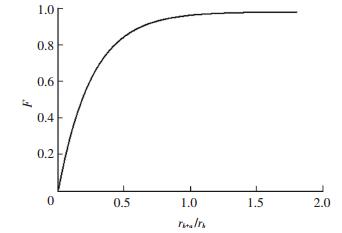
从图 3可知比例系数随裂隙增大而增加,(r+α)/r>1.5时,F→1.0.由裂隙破坏标准K1>KIC,得出裂隙破坏条件为
|
图 3 F值曲线 Figure 3 The F value curve |
| $ {P_0} > {K_{{\rm{IC}}}}/F\sqrt {{\rm{\pi }}\left( {r + \alpha } \right)} . $ | (19) |
爆生气体压力大于裂隙扩展的临界值,即驱动力
爆生气体作用过程中,速度随着裂隙的变化而变化,将式(17)反推求得任意时刻裂隙瞬时长度后对时间求导,便可得到扩展速度为
| $ V = \frac{{\partial \alpha }}{{\partial t}} = - \frac{{{\rm{\pi }}r_b^2}}{{2b\gamma {p_0}}}{\left( {\frac{{{p_0}}}{p}} \right)^{\frac{{1 + \gamma }}{\gamma }}}\frac{{{\rm{d}}P}}{{{\rm{d}}t}}. $ | (20) |
将式(18)中膨胀压力对时间求导数,可得膨胀压力变化速率为
| $ \frac{{{\rm{d}}P}}{{{\rm{d}}t}} = - \frac{{\alpha {C_0}{P_0}}}{A}{\left( {\frac{A}{{{C_0}t - B}}} \right)^{\alpha + 1}}. $ | (21) |
爆生气体作用下裂隙的扩展速度可将式(18)、(20)代入式(20)求得:
| $ V = \frac{{{\rm{\pi }}r_b^2\alpha {C_0}}}{{2b\gamma z}}{\left( {\frac{Z}{{{C_0}t - H}}} \right)^{\frac{{\gamma - \alpha }}{\gamma }}}. $ | (22) |
爆生气体作用并非绝热过程,故k=3的等熵膨胀渐变转化为γ=1.4的绝热膨胀.因此r=α时扩展速度最大达到极限值Vm=πr2C0/2bZ.取V=0.25Vm[11],故裂隙平均宽度为
| $ b = {\rm{\pi }}{r^2}{C_0}/0.76Z. $ | (23) |
根据爆生气体压力与裂隙扩展的临界值关系,可知裂隙是否继续发生破坏.当rb+α/rb>1.5时,F→1.0,裂隙扩展停止,故止裂状态方程为
| $ {P_m} = {K_{{\rm{IC}}}}/\sqrt {{\rm{\pi }}\left( {r + {\alpha _m}} \right)} . $ | (24) |
式中: Pm为裂隙停止扩展时的气体压力, αm为总裂隙长度.将Pm和αm代入式(17)并联立方程(23)、(24)可得爆生气体作用下最终裂隙扩展长度为
| $ {\alpha _m} = \frac{{\left[ {{\rm{\pi }}{r^2}/\log \left( {\gamma /{P_0}} \right)} \right] - {\rm{\pi }}{r^2}}}{{2b}}. $ | (25) |
工程爆破是多种应力场综合作用过程,起爆初期以应力波破坏为主,对岩体原始裂纹裂隙进行扩展;在应力波破坏的同时,爆生气体不断膨胀对裂纹裂隙进一步扩展贯穿.部分学者[12-14]分析指出,微差爆破过程不能单独考虑应力波或者爆生气体作用,而应当是两者综合作用的结果,但均未给出具体数学计算公式或理论模型.哈努卡耶夫[15]提出,最佳起爆间隔时间应当是爆生气体膨胀到一定程度沿裂隙冲出,将应力波作用产生的粉碎区和裂隙区连接并扩大贯穿,使得先爆炮孔刚好形成爆破漏斗的时间点,其间隔时间半经验公式为
| $ T = {t_1} + {t_2} + {t_3} = \frac{{2W}}{C} + \frac{R}{{{V_t}}} + \frac{S}{{{V_a}}}. $ | (26) |
式中:t1为弹性应力波传至自由面并返回时间;t2为裂缝形成时间;t3为破碎岩石离开母岩距离S的时间;W为最小抵抗线;C为弹性纵波速度;R为应力波破坏半径;Vt为应力波作用下裂缝扩展速度;S为爆生气体拓展的裂缝宽度;Va为爆生气体作用下裂隙扩展速度.
文献[15]给出了延期时间选取的半经验公式,但其参量取值多以经验值为主,缺乏理论依据.本文根据上述推出的应力波和爆生气体作用有关数学公式对哈努卡耶夫半经验公式进行修正.将式(12)、(14)、(22)、(23)带入式(26)可得延期间隔时间理论模型为
| $ \Delta t = {t_1} + {t_2} + {t_3} = \frac{{2W}}{C} + \frac{{2A}}{{{V_t}}} + \frac{b}{V}, $ | (27) |
其中:
| $ \begin{array}{*{20}{c}} {C = \sqrt {\lambda + 2u/\rho } = \sqrt {\left( {1 - v} \right)E/\left( {1 + v} \right)\left( {1 - 2v} \right)\rho } ;}\\ {{V_t} = 0.05Cb = {\rm{\pi }}{r^2}{C_0}/0.76Z;}\\ {V = \frac{{{\rm{\pi }}r_b^2\alpha {C_0}}}{{2b\gamma z}}{{\left( {\frac{Z}{{{C_0}t - H}}} \right)}^{\frac{{\gamma - \alpha }}{\gamma }}}.} \end{array} $ |
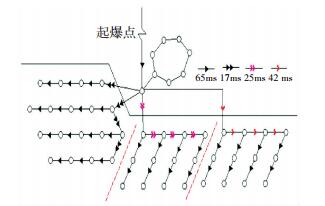
在青海德尔尼露采场4 278 m平台进行3次不同段别的高精度澳瑞凯雷管组合的逐孔台阶微差爆破实验,整个过程将某一爆区划分为1#区、2#区、3#区,进行肩并肩对比.采用逐孔起爆方式,孔内统一用400 ms延期雷管,3个实验区排间统一采用65 ms延期雷管、孔间分别采用17、25、42 ms雷管,即(65 ms、17 ms)、(65 ms、25 ms)、(65 ms、42 ms)组合雷管,具体爆破网络、爆区地质环境和爆后效果如图 4~8所示.
|
图 4 爆破网络 Figure 4 Blasting network |

|
图 5 爆区地质环境 Figure 5 The geological environment of blasting area |

|
图 6 1#爆区爆后效果 Figure 6 The blasting effect chart of 1# area |

|
图 7 2#爆区爆后效果 Figure 7 The blasting effect chart of 2# area |

|
图 8 3#爆区爆后效果 Figure 8 The blasting effect chart of 3# area |
从3个爆区爆后效果图可以看出,1#爆区(65 ms、17 ms)留有少量根底和大块,且塌落线不明显,爆堆不规整;2#爆区(65 ms、25 ms)爆后效果较好,无根底、大块,爆堆规整、连续、松散度较佳,有效节省了后期铲装、运输和二次爆破成本;3#爆区(65 ms、42 ms)爆后台阶垮裂、沉降以及前移效果明显,但碎岩被抛出距离较远,爆堆分散,加大了后期处理成本.故3种不同段别雷管组合爆破方案中,以孔间延期时间t=25 ms爆后效果最佳.
3.2 理论模型的计算露采场4 278 m平台岩性主要以蛇纹岩为主,具体岩石力学性质见表 1.
| 表 1 岩石力学性质统计 Table 1 Statistical table of rock mechanical propertys |
此次爆破实验采用深孔台阶爆破,孔间距为5 m、排间距为6 m、孔半径r=75 mm、孔深为14.5 m,岩石力学参数采用取样孔ZK001中数据为准,岩石密度ρ=2.58 g/cm3、最小抵抗线W=9 m.将参数代入式(26)计算延期时间可得Δt=t1+t2+t3=23.6 ms.依据本文修正后的最佳延期时间数学模型得此次爆破方案理论上最佳延期时间为24 ms左右,说明该理论模型与本次实验结果较为吻合.
4 结论1)结合岩体破碎理论、波动学理论、热力学理论以及断裂力学理论推导出微差台阶爆破工程中应力波、爆生气体运动方程和动力学方程,以此构建出了应力波和爆生气体破坏范围、作用时间和传播速度的数学公式.
2)基于本文推出的应力波和爆生气体动力和运动方程,对哈努卡耶夫提出的微差爆破延期时间半经验公式进行了修正,理论上给出了依据爆破能量释放形式为依据的最佳延期时间数学模型.微差爆破实验证明该数学理论模型计算结果与实验效果较为吻合.
| [1] | ZHENG Junjie, LOU Xiaoming, LUO Depi. Vibration superposition in tunnel blasting with millisecond delay[J]. Journal of Southwest Jiaotong University (English Edition), 2009, 17 (1) : 42-46. |
| [2] |
陈士海, 燕永峰, 戚桂峰, 等. 微差爆破降震效果影响因素分析[J].
岩土力学, 2011, 32 (10) : 21-26.
CHEN Shihai, YAN Yongfeng, QI Guifeng, et al. Analysis of influence factors of interference vibration reduction of millisecond blasting[J]. Rock and Soil Mechanics, 2011, 32 (10) : 21-26. DOI: 10.3969/j.issn.1000-7598.2011.10.018 |
| [3] | YAMAMOTO M, NODA H, KANEKO K. Experimental study on blast vibration control method which is based upon wave interference[J]. Journal of the Japan Explosive Society, 2008, 59 (5) : 231-240. |
| [4] | MOGI G, HOSHINO T, ADACHI T, et al. Consideration on local blast vibration control by delay blasting[J]. Journal of the Japan Explosive Society, 2009, 60 (5) : 233-239. |
| [5] |
李洪涛, 杨兴国, 卢文波, 等. 基于等效峰值能量的建筑物爆破振动安全评价探讨[J].
岩土工程学报, 2011, 33 (5) : 821-825.
LI Hongtao, YANG Xingguo, LU Wenbo, et al. Safety assessment for structures under blasting vibration based on equivalent peak energy[J]. Chinese Journal of Geotechnical Engineering, 2011, 33 (5) : 821-825. |
| [6] |
凌同华, 李夕兵. 基于小波变换的时-能分布确定微差爆破的实际延迟时间[J].
岩石力学与工程学报, 2003, 23 (13) : 2266-2270.
LING Tonghua, LI Xibing. Time-energy analysis based on wavelet transform for identifying real delay time in millisecond blasting[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 23 (13) : 2266-2270. |
| [7] | LU Yong, HAO Hong, MA Guowei, et al. Simulation of structural response under high-frequency ground excitations[J]. Earthquake Engineering & Structural Dynamics, 2001, 30 (3) : 307-325. DOI: 10.1002/eqe.8 |
| [8] |
王明洋, 王立云, 戚承志, 等. 爆炸荷载作用下岩石的变形与破坏研究(Ⅱ)[J].
防灾减灾工程学报, 2003, 23 (3) : 9-20.
WANG Mingyang, WANG Liyun, QI Chengzhi, et al. Study of def ormation and failure of rock under explosion load (part Ⅱ)[J]. Journal of disaster prevention and mitigation engineering, 2003, 23 (3) : 9-20. DOI: 10.3969/j.issn.1672-2132.2003.03.002 |
| [9] |
葛涛, 王明洋. 坚硬岩石在强冲击荷载作用下近区的性状研究[J].
爆炸与冲击, 2007, 27 (4) : 306-311.
GE Tao, WANG Mingyang. Characters near strong impact loading zone in hard rock[J]. Explosion and Shock Waves, 2007, 27 (4) : 306-311. DOI: 10.3321/j.issn:1001-1455.2007.04.003 |
| [10] | 沈成康. 断裂力学[M]. 上海: 同济大学出版社, 1996 : 43 -65. |
| [11] | 戴俊. 岩石动力学特性与爆破理论[M]. 北京: 冶金工业出版社, 2013 : 52 -53. |
| [12] | 戚承志, 钱七虎. 岩体动力变形与破坏的基本问题[M]. 北京: 科学出版社, 2009 : 65 -94. |
| [13] | GRADY D E, KIPP M E. Continuum modeling of explosion fracture in oil shale[J]. International Journal of Rock Mechanics and Sciences andGeomechanics Abstracts, 1987, 17 (3) : 147-157. DOI: 10.1016/0148-9062(80)91361-3 |
| [14] | SAHARAN M R, MITRI H S. Numerical procedure for dynamic simulation of discrete fractures due to blasting[J]. Rock Mechanics and Rock Engineering, 2008, 41 (5) : 641-670. DOI: 10.1007/s00603-007-0136-9 |
| [15] | 哈努卡耶夫. 矿岩爆破物理过程[M]. 北京: 北京冶金工业出版社, 1980 : 446 -529. |
 2017, Vol. 49
2017, Vol. 49


