2. 东南大学 电子科学与工程学院,南京 210096
2. College of Electronic Science and Engineering, Southeast University, Nanjing 210096, China
随着航天活动规模的扩大和任务的多样化,液氧/甲烷 (LOX/CH4) 推进剂组合更适用于在轨时间长的深空探测发动机和下降级发动机[1]. LOX/CH4膨胀循环发动机启动过程工况变动大,故障发生概率高[2].从推进剂充填到强迫充填过程的转换过程中,由于启动涡轮泵、阀门开启以及火药启动器和燃气发生器工作交叠,呈现非线性特性,建立较为精确、能实时在线处理的发动机启动过程的模型比较困难[3].目前国内外关于液体火箭发动机故障诊断方法包括航天飞机主发动机 (SSME) 实时故障诊断的LEADER系统[4]、基于独立分量分析研究液体火箭发动机故障诊断方法[5]、基于主元分析 (KPCA) 和支持向量多分类机 (SVM) 的故障诊断方法[6]、将关联规则技术应用于发动机启动过程故障检测[7]等.随着液体火箭发动机健康监控和故障诊断技术的发展,这些方法也不断地更新和优化,但仍然存在着阈值合理性确定难,关联规则数太多以及诊断规则需要依赖于大量的先验条件等缺陷.
Petri网最早应用于故障识别与诊断,通过监测库所不变量中标识的变化而引入,文献[8]主要通过标签Petri网构建ABS系统模型从而检测出该系统中存在的故障问题.文献[9]利用Petri网中的库所不变量的方法来寻找系统的故障.文献[10-11]通过分析Petri网的结构信息,增加传感器的数量来提高故障诊断的准确性.本文针对LOX/CH4膨胀循环发动机启动过程中存在的故障诊断效率低,诊断延时性大等问题,在现有研究成果的基础上,提出一种基于部分可观Petri网结构特点的在线故障诊断算法,分析系统可观事件和可观系统状态,推算观测序列集中不可观变迁点火情况,诊断观测序列集中包含的故障,并通过实验仿真,验证算法的有效性.
1 部分可观Petri网故障诊断问题 1.1 部分可观Petri网定义1 Petri网 (Petri nets,PN) 定义为一个四元组:G= < P, T, WPR, WPO >, 其中P={P1…Pn}为一个n维的库所集;T={T1…Tq}为一个q维的变迁集;WPR∈(N)n×q、WPO∈(N)n×q为连接库所和变迁弧的前、后关联矩阵,定义矩阵W=WPO-WPR为PN的关联矩阵,其维数n×q(N为非负整数集). M0为初始标签向量,M为PN的标签向量.当且仅当M≥WPR(:, j),WPR(:, j) 为j处的列向量,变迁Tj在标识M处点火, 记为M[Tj>.如果Tj点火后有ΔM=M′-M=WPR(:, j),则M[Tj>M′.
已知点火序列σ=T(1)T(2)…和变迁Tj∈T,j=1, …, h,标识M处的点火序列的长度用h=|σ|表示. xj(σ) 为点火序列中变迁Tj发生的次数,X (σ)=(xj(σ)) 表示点火序列σ的点火数向量.
如果存在一个点火序列σ, 标识M可以通过初始标识MI变迁得到,则MI[σ>M变迁得到{M1, M2, M3, …}, 记为R(G, M0).
定义2 部分可观Petri网 (partially observed Petri nets,POPN) 给定三元组G0= < G, L, H>,G是一个PN结构,L和H分别为事件和标识传感器矩阵.事件传感器矩阵L为每个过渡矩阵分配一个标识,H ={e1, …ep}为观测变迁的p维标识集合,不可观测变迁向量用ε表示,标识间的级联满足:ε·ε=ε,ε ·ek=ek.标识ek由p维向量表示,ek=(ekj),ekj≠0, k≠j,ekk=1.空标识ε用p维零向量ε= 0p表示.事件矩阵L=(lkj)∈(N)p×q,当L·X(Tj)=ek时,lkj=1,否则lkj=0.标识矩阵H∈Rn0×n表示标识的投影向量M在实数域内没有子集 (R实数集).
1.2 观测序列对于任意标识M和变迁T,存在M[T>M′,M ∈R(G, M0),定义Mo=M·H,Mo′=H·M′,eo=L·X(T).如果Mo′≠Mo或eo≠ε则将观测矩阵TRo(T, M) 定义为TRo(T, M)=eoMo′.当一个未发生变迁点火 (eo=ε),或标识未改变Mo=Mo′,无法收集信息,即TRo(T, M)=ε.
定义3 带标识POPN < G0, M0 >模型化离散事件系统,标识M处观测序列TRo(σ, M),长度为h的点火序列σ=T(1)…T(t)…T(h).在标识M处M∈R(G, M0),点火序列σ被连续点火,表示为M[T(1) > M(1)…[T(h) > M(h),将这一过程称为观测序列级联,写作:
| $ \begin{gathered} \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{R}}_{\rm{o}}}\left( {\mathit{\boldsymbol{\sigma }},\mathit{\boldsymbol{M}}} \right) = {\mathit{\boldsymbol{M}}_{\rm{o}}}\left( 0 \right)\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{R}}_{\rm{o}}}\left( {\mathit{\boldsymbol{T}}\left( 1 \right),\mathit{\boldsymbol{M}}} \right) \cdots \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{R}}_{\rm{o}}}\left( {T\left( h \right),} \right. \hfill \\ \left. {\mathit{\boldsymbol{M}}\left( {h - 1} \right)} \right) = {\mathit{\boldsymbol{M}}_{\rm{o}}}\left( 0 \right){\mathit{\boldsymbol{e}}_{\rm{o}}}\left( 1 \right){\mathit{\boldsymbol{M}}_{\rm{o}}}\left( 1 \right){\mathit{\boldsymbol{e}}_{\rm{o}}}\left( 2 \right) \cdots {\mathit{\boldsymbol{e}}_{\rm{o}}}\left( {{h_{\rm{o}}}} \right){\mathit{\boldsymbol{M}}_{\rm{o}}}\left( {{h_{\rm{o}}}} \right), \hfill \\ \end{gathered} $ | (1) |
其中Mo=M·H,观测序列的长度ho≤h.
定义4[11] 对于有界PN系统,如果变迁Tj∈T,可达系统标识组 (Mi, Mk),Mi[Tj>Mk,L ·X(Tj)=ε,H ·WPR(:, j)=H·WPO(:, j),则aεik=1;否则aεik=0,把Aε=(aεik)N×N,aεik∈{0, 1}称为系统的诱导不可达矩阵.对于无界PN系统,Aε通过网系统的极值点分离图获得.
2 部分可观Petri网在线故障诊断方法 2.1 部分可观Petri故障诊断定理1[12] 给定POPN < G0, M0 >系统和N维诱导不可观矩阵Aε,传感器的配置 (L, H).当且仅当 (Aε)N=0时,任意与基本观测序列对应的基本点火序列是有限的,且|σ|≤hmax.
| $ {h_{\max }} = \min \left\{ {h|{\mathit{\boldsymbol{A}}_\varepsilon }^h = 0} \right\},h \geqslant 0. $ | (2) |
定理1描述的是与基本观测序列相对应的基本点火序列的上边界值hmax的计算方法.对于有界PN系统,hmax的计算复杂性取决于可达集的基集;对于无界PN系统,则取决可覆盖图极点的数量.为了避免存在无穷个基本点火序列,本文的研究中,假设不改变标识测量的不可观点火序列有界,基本点火序列的最大长度为hmax,未点火变迁的最大长度为hmax-1,且任意事件的不可观序列中,未点火变迁可以被不可观标识连续点火.
定理2[13-14] 标识POPN < G0, M0 >系统模型化离散事件系统,若M∈R∞(G, M0) 不改变标识测量的不可观点火序列有界,存在H·M=M0(0) 满足不等式 (3) 和等式 (4), 则与观测序列对应的点火序列σ= T(1, 1)…T(1, h1)T(2, 1)…T(ho, 1)…T(ho, ho), 其中,hk < hmax,k=1, …ho,ho为可观矩阵TRo的长度.
| $ \left( {\begin{array}{*{20}{c}} { - {\mathit{\boldsymbol{I}}_q}} & {\bf{0}} & \cdots & {\bf{0}} \\ {\bf{0}} & { - {\mathit{\boldsymbol{I}}_q}} & \ddots & \vdots \\ \vdots & \ddots & \ddots & {\bf{0}} \\ {\bf{0}} & \cdots & {\bf{0}} & { - {\mathit{\boldsymbol{I}}_q}} \\ {{{\left( {{\mathit{\boldsymbol{l}}_q}} \right)}^{\rm{T}}}} & {\bf{0}} & \cdots & {\bf{0}} \\ {\bf{0}} & {{{\left( {{\mathit{\boldsymbol{l}}_q}} \right)}^{\rm{T}}}} & \ddots & \vdots \\ \vdots & \ddots & \ddots & {\bf{0}} \\ {\bf{0}} & \cdots & {\bf{0}} & {{{\left( {{\mathit{\boldsymbol{l}}_q}} \right)}^{\rm{T}}}} \\ {{\mathit{\boldsymbol{W}}_{{\rm{PR}}}}} & {\bf{0}} & \cdots & {\bf{0}} \\ { - \mathit{\boldsymbol{W}}} & {{\mathit{\boldsymbol{W}}_{{\rm{PR}}}}} & \ddots & \vdots \\ \vdots & \ddots & \ddots & {\bf{0}} \\ { - \mathit{\boldsymbol{W}}} & \cdots & { - \mathit{\boldsymbol{W}}} & {{\mathit{\boldsymbol{W}}_{{\rm{PR}}}}} \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{X}}\left( {T\left( {1,1} \right)} \right)} \\ \vdots \\ {\mathit{\boldsymbol{X}}\left( {T\left( {1,{h_1}} \right)} \right)} \\ {\mathit{\boldsymbol{X}}\left( {T\left( {2,1} \right)} \right)} \\ \vdots \\ {\mathit{\boldsymbol{X}}\left( {T\left( {2,{h_2}} \right)} \right)} \\ \vdots \\ {\mathit{\boldsymbol{X}}\left( {T\left( {{h_{\rm{o}}},{h_{{h_{\rm{o}}}}}} \right)} \right)} \end{array}} \right) \leqslant \left( {\begin{array}{*{20}{c}} {{{\bf{0}}_q}} \\ {{{\bf{0}}_q}} \\ \vdots \\ {{{\bf{0}}_q}} \\ 1 \\ 1 \\ \vdots \\ 1 \\ \mathit{\boldsymbol{M}} \\ \mathit{\boldsymbol{M}} \\ \vdots \\ \mathit{\boldsymbol{M}} \end{array}} \right), $ | (3) |
| $ \begin{gathered} \left( {\begin{array}{*{20}{c}} \mathit{\boldsymbol{L}} & {\bf{0}} & \cdots & {\bf{0}} \\ {\bf{0}} & \ddots & {} & \vdots \\ \vdots & {} & \mathit{\boldsymbol{L}} & {\bf{0}} \\ {\bf{0}} & \cdots & {\bf{0}} & \mathit{\boldsymbol{L}} \\ {\mathit{\boldsymbol{HW}}} & {\bf{0}} & {} & {\bf{0}} \\ {\bf{0}} & \ddots & {} & \vdots \\ {\bf{0}} & {} & {\mathit{\boldsymbol{HW}}} & {\bf{0}} \\ {\mathit{\boldsymbol{HW}}} & {\mathit{\boldsymbol{HW}}} & {\mathit{\boldsymbol{HW}}} & {\mathit{\boldsymbol{HW}}} \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{X}}\left( {T\left( {k,1} \right)} \right)} \\ \vdots \\ {\mathit{\boldsymbol{X}}\left( {T\left( {k,{h_k} - 1} \right)} \right)} \\ {\mathit{\boldsymbol{X}}\left( {T\left( {k,1} \right)} \right)} \end{array}} \right) = \hfill \\ {\left( {\begin{array}{*{20}{c}} {{{\bf{0}}_p} \cdots {{\bf{0}}_p}} & {{\mathit{\boldsymbol{e}}_0}\left( k \right)} & {{{\bf{0}}_n} \cdots {{\bf{0}}_n}} & {{\mathit{\boldsymbol{M}}_0}\left( k \right) - {\mathit{\boldsymbol{M}}_0}\left( {k - 1} \right)} \end{array}} \right)^{\rm{T}}}. \hfill \\ \end{gathered} $ | (4) |
定义与基本观测序列对应的点火序列集为∑TRo,∑TRo={σ‖σ‖≤hmax·ho},σ满足定理2.设∑TRo中不包含以未点火变迁结束的点火序列,点火序列是否点火不影响标识的测量,则∑TRo的计算复杂性正相关于方程组 (3)、(4) 的计算复杂性.
定理3 标识POPN < G0, M0 >系统模型化离散事件系统.如果存在长度为ho的观测序列TRo,对于任意点火序列σ(σ∈∑(TRo)) 都能满足关系式min{Fα·X(σ)} > 0(或者为max{Fα·X(σ)}=0),则观测序列中一定存在故障 (或一定不存在故障).
证明 如果任意点火序列σ(σ∈∑(TRo)) 都能满足min{Fα·X(σ)} > 0,在观测序列集∑TRo中,点火序列对应的点火数向量非零,由此可知∑TRo中的任何一个点火序列中至少包含一个故障变迁集.故障集存在于观测序列TRo中;同理,对于任意点火序列σ∈∑(TRo) 都满足max{Fα·X(σ)}=0,则TRo中不存在故障集.
定理3给出了故障诊断的充分非必要条件,利用整数线性规划解决故障的诊断问题.但若存在点火序列σ使Fα·X(σ) > 0,同时存在σ′∈∑(TRo),使Fα·X(σ′)=0,则不能完全判定故障存在与否.当传感器配置太低或者观测序列太短时,这种情况很可能发生.为了避免计算过程中模糊信息的出现,定义置信度Fbelief和置信因子Fdiag来优化判定方法.
定义5 观测序列中故障集出现的可信度称为置信度,用Fbelief表示.故障诊断后,故障发生置信度的有效程度称为置信因子,用Fdiag表示.
| $ \begin{gathered} \;\;\;\;\;\;{F_{{\rm{belief}}}}\left( {\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{R}}_{\rm{o}}},{\mathit{\boldsymbol{f}}_\alpha }} \right) = \hfill \\ {P_i}\left( {\frac{{{\rm{card}}\left( {\mathit{\boldsymbol{\sigma }} \in \sum {\left( {\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{R}}_{\rm{o}}}} \right)} ,{\mathit{\boldsymbol{F}}_\alpha } \cdot \mathit{\boldsymbol{X}}\left( \mathit{\boldsymbol{\sigma }} \right) > 0} \right)}}{{{\rm{card}}\left( {\mathit{\boldsymbol{\sigma }} \in \sum {\left( {\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{R}}_{\rm{o}}}} \right)} } \right)}}} \right) \in \left[ {0:1} \right], \hfill \\ \end{gathered} $ | (5) |
| $ {F_{{\rm{diag}}}}\left( {\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{R}}_{\rm{o}}},{\mathit{\boldsymbol{f}}_\alpha }} \right) = 4{\left( {{F_{{\rm{belief}}}}\left( {\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{R}}_{\rm{o}}},{\mathit{\boldsymbol{f}}_\alpha }} \right) - 0.5} \right)^2}, $ | (6) |
card (σ∈∑(TRo)) 为观测序列集∑TRo的子集,表示所有点火序列σ∈∑(TRo) 的集合.
card (σ∈∑(TRo), Fα·X(σ) > 0) 为满足Fα·X(σ)>0的所有点火序列σ∈∑(TRo) 的集合. Pi为观测序列集∑TRo(σ, M0) 中观测序列被观测到的概率. Fbelief和Fdiag均为0到1之间的一个有理数.结合定义5和定理3,推出故障判定的充要条件:当min{Fα·X(σ)} > 0对于任意σ∈∑(TRo) 都满足时,如果故障置信度等于1且置信因子等于1,故障集存在;当max{Fα·X(σ)}=0对于任意σ∈∑(TRo) 都满足时,如果故障置信度等于0且置信因子等于1,故障集不存在;最坏情况即为故障发生置信度为0.5而置信因子等于0,无法判定是否存在故障.
2.2 故障诊断算法根据上节提出的故障判定方法,构建关于给定故障集的线性成本函数,采用分支定界法来解决[15].本文在此基础上,结合向前-向后函数,提出一种基于部分可观Petri网的在线故障诊断算法如下.
输入:fα和K
输出:fbw(k), ffw(k), Fbelief(TRo(Ik), fα)
1) 获取观测序列TRo(k)
2) 初始化数据变量:fbw(k)←0, ffw(k)←0,
Ik←(k-fbw(k), k+ffw(k))
3) 计算;Fbelief(TRo(Ik), fα)
While (0 < Fbelief(TRo(Ik), fα) < 1 &
fbw(k) < min (k-1, K))
fbw(k)=fbw(k)+1,
Ik←(k-fbw(k), k+ffw(k))
Computer Fbelief(TRo(Ik), fα);
End While;
Return fbw(k), ffw(k), Fbelief(TRo(Ik), fα)
4) 检测序列中故障Fbelief(TRo(Ik), fα)
For j=k-1:-1:max (1, k-K)
If 0 < Fbelief(TRo, fα) < 1
fbw(k)←0,
ffw(k)←k-j,
Ij=(j-fbw(j), j+ffw(j))
Computer Fbelief(TRo(Ik), fα)
While (0 < Fbelief(TRo(Ik), fα) < 1 &
fbw(k) < min (j-1, K-k+j))
fbw(k)←fbw(k)+1,
Ij=(j-fbw(j), j+ffw(j))
Update Fbelief(TRo(Ik), fα)
End While
Update fbw(k), ffw(k), Fbelief(TRo(Ik), fα)
End If
End For
5) 返回重新开始
Goto Start
2.3 算法分析长度为ho的可观序列,如果存在K>0,1≤k≤ho,若观测序列中出现明确的故障,算法返回置信度Fbelief(TRo(Ik), fα)=1.从k=1枚举,对给定观察序列进行连续观测.对于任意k′≥k≥1,定义TRo(k, k′)=M0(k-1)eo(k)M0(k)…M0(k′-1)eo(k′)M0(k′)∈TRo,TRo(k, k′) 是观测序列TRo(k) 的子序列.对于存在模糊信息的观测序列,先对其使用向后算法 (backward),得到TRo(k)TRo(k-1, k)…TRo(1, k);如果模糊决策仍然存在,再启用向前算法 (forward).如果长度为K的观测序列中仍未有明确的结论,结束本次诊断返回置信度的值.继续诊断第k+1个观测序列TRo(k, k+1),TRo(k-1, k+1),…,TRo(1, k+1),TRo(1, k+2),…是否满足约束条件.每次诊断完成后,算法会输出3个变量: ffw(k)∈(0, …, K)、fbw(k)∈(0, …, K)、Fbelief(TRo(Ik), fα),其中满足fbw(k)+ffw(k)≤K,XIk=(k-fbw(k), k+ffw(k)).
计算过程中可能出现的情况:1) 存在fbw(k)∈ (0, …, K),ffw(k)∈(0, …, K),且有fbw(k)+ffw(k)≤K,对于任意σ∈∑(TRo) 始终存在Fα·X(σ)>0.此时Fbelief(TRo(Ik), fα)=1,即故障存在. 2) 存在fbw(k)∈(0, …, K),ffw(k)∈(0, …, K),且有fbw(k)+ffw(k)≤K,对于任意σ∈∑(TRo) 始终存在Fα·X(σ)=0.此时Fbelief(TRo(Ik), fα)=0,故障不存在. 3) 存在fbw(k)∈(0, …, K),ffw(k)∈(0, …, K),且有fbw(k)+ffw(k)≤K满足0 < Fbelief(TRo(Ik), fα) < 1,则故障可能发生.
3 实例分析与验证中国航天科技六院101所通过各类挤压试验、联动试验、点火试验等,以中国新一代液氧煤油火箭发动机YF-77为基础研制的60吨级液氢甲烷火箭发动机[16].
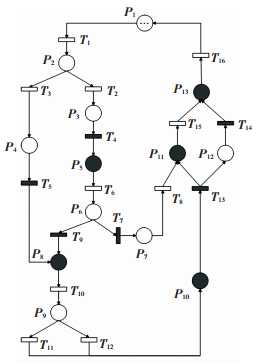
3.1 LOX/CH4膨胀循环发动机启动过程本文对YF-77膨胀循环发动机启动过程进行研究,建立了LOX/CH4膨胀循环发动机启动过程部分可观Petri网模型,如图 1所示.
|
图 1 LOX/CH4膨胀循环发动机启动过程部分可观Petri网模型 Figure 1 The POPN model of the LOX/CH4 expander cycle engine start-up process |
图 1以发动机启动过程中关键节点为库所,关键动作为变迁建立网模型,模拟启动阶段的运行过程,各库所和变迁的含义见表 1、2.
LOX/CH4膨胀循环发动机启动过程:发动机各部件准备就绪,启动按钮启动,火药起动器点火驱动起动涡轮转动,主涡轮泵起旋.氧气储存室接到启动信号后检测储存室氧气存储量,氧气存储充足的情况下打开储存室阀门,经氧泵增压后,通过氧主气蚀管,进入氧主阀前.
甲烷气路接到启动信号后检测甲烷燃料室储量、燃料室冷却通道温度,甲烷充足、冷却通道温度满足设定值时,燃料室阀门打开.液态甲烷经燃料室冷却通道升温,在甲烷涡轮前分成两部分:一部分流经调节阀分流到氧涡轮出口;另一部分直接驱动甲烷涡轮,之后再分为两路,大部分进入氧涡轮推动氧涡轮运转,小部分甲烷经电动调节阀分流到氧涡轮出口,汇总后进入燃烧室.氧主阀和甲烷主阀打开后,氧气和甲烷以不同比例汇入推力室,经加压点火后在燃烧室内燃烧.此外,甲烷涡轮和氧涡轮旁路分别并联调节阀,用于实现推力和混合比调节.
3.2 LOX/CH4膨胀循环发动机故障诊断根据液体发动机组成结构层次分解方法,膨胀循环发动机可分解为涡轮、泵、热力组件、液体管路、带阀液体管路等主要部件[5].以火箭发动机甲烷涡轮机故障为例,验证本故障诊断方法的有效性.
3.2.1 故障诊断数学模型设故障集F={f1}, f1=T4甲烷涡轮出现故障,涡轮机转子被卡住;LOX/CH4膨胀循环发动机启动过程的Petri网故障诊断模型主要参数可观变迁集H、初始标识M0、事件矩阵L. H={e1, e2, e3, ε4, ε5, e6, ε7, ε9, e10, e11, e12, ε13, e8, ε14, ε15, e16},M0=(3000000000000000),L =
| $ \left[ {\begin{array}{*{20}{c}} 1&0&{}&{}&{}&{}&{}&{}& \cdots &{}&{}&{}&{}&{}&{}&0\\ 0&1&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}&0\\ {}&{}&1&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}\\ {}&{}&{}&0&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}\\ {}&{}&{}&{}&0&{}&{}&{}&{}& \ddots &{}&{}&{}&{}&{}&{}\\ {}&{}&{}&{}&{}&1&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}\\ {}&{}&{}&{}&{}&{}&0&{}&{}&{}&{}&{}&{}&{}&{}&{}\\ \vdots &{}&{}&{}&{}&{}&{}&0&{}&{}&{}&{}&{}&{}&{}& \vdots \\ {}&{}&{}&{}&{}&{}&{}&{}&1&{}&{}&{}&{}&{}&{}&{}\\ {}&{}&{}&{}&{}&{}&{}&{}&{}&1&{}&{}&{}&{}&{}&{}\\ {}&{}&{}&{}&{}&{}&{}&{}&{}&{}&1&{}&{}&{}&{}&{}\\ {}&{}&{}&{}&{}& \ddots &{}&{}&{}&{}&{}&0&{}&{}&{}&{}\\ {}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}&1&{}&{}&{}\\ {}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}&0&{}&{}\\ 0&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}&{}&0&0\\ 0&{}&{}&{}&{}&{}&{}& \cdots &{}&{}&{}&{}&{}&{}&0&1 \end{array}} \right]. $ |
通过方程组 (3)、(4),求得诊断序列对应的点火序列σ和观测序列集∑TRo(σ, M0). σ=T1, T2, T3, T4, T5, T6, T7, T9, T10, T11, T12, T13, T8, T14, T15, T16,∑TRo(σ, M0)=
| $ \left[ {\begin{array}{*{20}{c}} {{e_1},{e_2},{e_3},\varepsilon ,\varepsilon ,{e_6},\varepsilon ,\varepsilon ,{e_{10}},{e_{11}},{e_{12}},\varepsilon ,{e_8},\varepsilon ,\varepsilon ,{e_{16}}} \\ {{e_1},{e_2},{e_3},\varepsilon ,\varepsilon ,{e_6},\varepsilon ,\varepsilon ,{e_{10}},{e_{11}},{e_{12}},\varepsilon ,{e_8},\varepsilon ,\varepsilon ,{e_{16}}} \\ {{e_1},{e_2},{e_3},\varepsilon ,{e_6},\varepsilon ,\varepsilon ,\varepsilon ,{e_{10}},{e_{11}},{e_{12}},\varepsilon ,{e_8},\varepsilon ,\varepsilon ,{e_{16}}} \\ {{e_1},{e_2},\varepsilon ,{e_3},\varepsilon ,{e_6},\varepsilon ,\varepsilon ,{e_{10}},{e_{11}},{e_{12}},\varepsilon ,{e_8},\varepsilon ,\varepsilon ,{e_{16}}} \\ {{e_1},{e_2},\varepsilon ,{e_6},{e_3},\varepsilon ,\varepsilon ,\varepsilon ,{e_{10}},{e_{11}},{e_{12}},\varepsilon ,{e_8},\varepsilon ,\varepsilon ,{e_{16}}} \\ {{e_1},{e_2},\varepsilon ,{e_3},{e_6},\varepsilon ,\varepsilon ,\varepsilon ,{e_{10}},{e_{11}},{e_{12}},\varepsilon ,{e_8},\varepsilon ,\varepsilon ,{e_{16}}} \\ {{e_1},{e_3},{e_2},\varepsilon ,\varepsilon ,{e_6},\varepsilon ,\varepsilon ,{e_{10}},{e_{11}},{e_{12}},\varepsilon ,{e_8},\varepsilon ,\varepsilon ,{e_{16}}} \\ {{e_1},{e_3},{e_2},\varepsilon ,\varepsilon ,{e_6},\varepsilon ,\varepsilon ,{e_{10}},{e_{11}},{e_{12}},\varepsilon ,{e_8},\varepsilon ,\varepsilon ,{e_{16}}} \\ {{e_1},{e_3},\varepsilon ,{e_2},\varepsilon ,{e_6},\varepsilon ,\varepsilon ,{e_{10}},{e_{11}},{e_{12}},\varepsilon ,{e_8},\varepsilon ,\varepsilon ,{e_{16}}} \\ {{e_1},{e_3},{e_2},\varepsilon ,{e_6},\varepsilon ,\varepsilon ,\varepsilon ,{e_{10}},{e_{11}},{e_{12}},\varepsilon ,{e_8},\varepsilon ,\varepsilon ,{e_{16}}} \end{array}} \right]. $ |
其中ei表示与点火序列中可观的点火变迁,ε表示不可观的点火变迁.
算法先选取参数K;然后诊断第k步基本观测序列TRo(k)=(*)ei(*) 中是否包含故障集,其中ei为第k步点火变迁,“*”为变迁点火前后变迁前集库所包含的托肯数;最后,计算每个基本观测序列中故障集发生的置信度Fbelief(TRo, f1) 和置信因子Fdiag(TRo, f1).
| $ \begin{gathered} \begin{array}{*{20}{c}} {{F_{{\rm{belief}}}}\left( {\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{R}}_{\rm{o}}},{\mathit{\boldsymbol{f}}_1}} \right) = {P_i}\left( {\frac{{{\rm{card}}\left( {\mathit{\boldsymbol{\sigma }} \in \sum {\left( {\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{R}}_{\rm{o}}}} \right)} ,{\mathit{\boldsymbol{f}}_1} \cdot \mathit{\boldsymbol{X}}\left( \mathit{\boldsymbol{\sigma }} \right) > 0} \right)}}{{{\rm{card}}\left( {\mathit{\boldsymbol{\sigma }} \in \sum {\left( {\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{R}}_{\rm{o}}}} \right)} } \right)}}} \right),} \\ {{F_{{\rm{diag}}}}\left( {\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{R}}_{\rm{o}}},{\mathit{\boldsymbol{f}}_1}} \right) = 4{{\left( {{F_{{\rm{belief}}}}\left( {\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{R}}_{\rm{o}}},{\mathit{\boldsymbol{f}}_1}} \right) - 0.5} \right)}^2},} \end{array} \hfill \\ \end{gathered} $ |
card (∑(TRo(k)) 为观测序列集∑TRo(σ, M0) 的子集. Pi(i=1…16) 为包含故障集的点火序列被点火的概率.
3.2.2 实例仿真计算本文进行的仿真实验采用双涡轮串联系统,发动机真空推力80 kN,室压3.75 MPa,发动机流量22.7 kg/s,混合比3:1,发动机真空比冲3 570 m/s,喷管面积比80,甲烷涡轮入口温度420 K,氧气泵泵后压力9.2 MPa,甲烷泵泵后压力13.4 MPa.
根据定理2和算法1选取参数K=5,诊断过程如下:k=1时,基本观测序列TRo(1)=(3)e1(0),变迁T1可观且满足点火条件,该序列不存在故障集. k=2时,基本观测序列TRo(2)=(3)e2(1),变迁T2可观且满足点火条件,该序列不存在故障集. k=3时,基本观测序列TRo(3)=(1)e3(0),变迁T3可观且满足点火条件,该序列不存在故障集. k=4时,基本观测序列TRo(4)=(2)ε(*),变迁T4不可观,通过已知信息不能确定变迁是否点火,变迁后集中托肯的数量不可观,因此无法诊断该序列是否包含故障, 为了解决这个问题,算法1引入向前算法,以TRo(4) 为中心,向前拓展基本观测序列得TRo(4)=(1)e3(0, 2)ε(*) 或 (3)e2(1, 1)e3(0, 2)ε(*),该序列仍不能提供足够的信息来判定T4是否点火,这时需在向前拓展后的基础上,应用向后算法,观测序列向后拓展1步为 (3)e2(1, 1)e3(0, 2)ε(*, 1)ε(*),拓展2步为 (3)e2(1, 1)e3(0, 2)ε(*, 1)ε(*, 2)e6(1),值得注意的是拓展长度不得超过取定K值,当观测序列拓展为TRo(4)=(3)e2(1, 1)e3(0, 2)ε(*, 1)ε(*, 2)e6(1) 时,根据可观变迁T2点火成功、可观变迁T6点火条件不足未点火可推知:T4不完全点火.不可观变迁T4出现故障,基本观测序列TRo(4)=(2)ε(*) 中包含故障f1.继续对k=5,k=6,…,k=16时的基本观测序列进行故障诊断,未发现故障f1.
3.2.3 故障诊断结果液涡轮主要存在于高压补燃发动机中,为预压泵提供轴动力[16].文中甲烷涡轮的主要故障是转子破坏、流道堵塞、轴承卡住、转子卡住和涡轮轮缘脱落,发生这些故障后涡轮效率下降甚至丧失提供动力的能力.火箭发动机启动过程各组件具有严格的启动顺序,针对不同的故障类型,需分别进行故障诊断.本文以变压器运行故障为例进行仿真实验,通过系统反馈各模块包含故障f1的置信度和置信因子,来判定各运行阶段的故障发生情况,具体实验结果如表 3所示.
| 表 3 故障诊断结果 (K=5) Table 3 The results of fault diagnosis (K=5) |
从表 3可知,k=4和k=5时,故障发生的置信度分别为1、0.95,即认为故障置信度为1,系统包含故障f1;k=7和k=12时,基本观测序列故障f1发生置信度为0,故障诊断结果为“可能存在故障”,表明该序列中不包含故障f1,但由于参数K限定了诊断序列的长度,无法确定该序列中的不可观变迁是否点火,即无法判定该序列中是否包含其他类故障.这种情况下,将该序列中包含的不可观变迁可能引发的故障类别设为诊断目标,更新参数K值,重新进行该类故障诊断.由表 3可以明确确定观测序列中存在故障,且故障发生的位置为T4.
3.3 LOX/CH4膨胀循环发动机部分可观Petri网故障诊断结果分析诊断过程采用互检原则,当多节点诊断过程中均因某节点故障而导致故障时,才认为系统在该节点处发生故障[6].为了降低计算复杂性、提高计算效率,算法引入参数K,主要用于限定诊断过程中拓展后的基本观测序列的长度hk,始终满足hk < K,即向前-向后函数只能将基本观测序列的长度拓宽到K.参数K提出使故障诊断时间线性相关于K,而非指数相关于观测序的长度ho,将计算时间降为原来的ho-1·eho-K,解决了随着系统复杂性增大、观测序列增长,诊断时间指数性增长的问题.
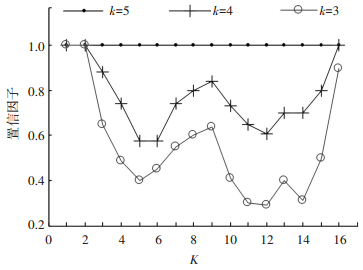
图 2为不同K值,诊断时间的变化.由图 2可知,当K等于3或4时,计算得到可观测序列中包含故障f1的置信因子大部分位于0和1之间,不能准确判定系统是否存在故障;当K等于5时,可观序列中故障f1发生的置信因子全部为1,即能够明确判定故障是否在系统中存在. 图 2中3条曲线的分布情况表明故障诊断的可信度随着K值的增大而增大.综上所述,算法中最优K值的选取对提高故障诊断效率具有决定性的作用.
|
图 2 参数K与置信因子的关系 Figure 2 The relationship of the parameter K and Fdiag |
为了验证部分可观Petri网的故障诊断算法对故障诊断的有效性,对系统进行多次、多类故障仿真实验.在不同位置设置不同故障类型,根据故障类别选定最优参数K,统计结果:1 000次实验中,设定有800次存在故障、200次不存在故障,实际算法诊断出793次故障、201次无故障、6次不确定是否存在故障,算法诊断的可信度为99.3%,根据以上数据,证明本文提出的故障诊断算法能够满足实际应用要求.
4 结论1) 采用加权置信度诊断算法,设定点火变迁故障发生概率;应用交互式诊断方式,引入参数K和向前-向后算法,根据诊断节点间变迁的点火与否、挖掘故障产生的根源,实现了对LOX/CH4膨胀循环发动机启动过程中的不可观事件和不可观运行状态进行在线故障诊断.
2) 在建立LOX/CH4膨胀循环发动机启动过程故障诊断的部分可观Petri网模型的基础上,基于软件仿真平台,对发动机启动过程进行了故障诊断仿真实验.仿真结果证明了所提出的算法能有效降低计算复杂性,适用于在线故障诊断.
3) 在今后的研究工作中,需进一步研究参数K选取的约束条件和优化计算方法,并将Petri网的状态结构信息与故障诊断算法相互融合等.
| [1] |
李艳军. 新一代大推力液体火箭发动机故障检测与诊断关键技术研究[D]. 长沙: 国防科技大学, 2014.
LI Yanjun. Study on key techniques of fault detection and diagnosis for new generation large-scale liquidpropellant rocket engines[D]. Changsha: National University, 2014. |
| [2] |
朱志新, 何小民, 薛冲, 等. 涡轮组合循环发动机超级燃烧室燃烧性能试验[J].
航空动力学报, 2013, 30(9): 2115-2121.
ZHOU Zhixin, HE Xiaomin, XUE Chong, et al. Experiment on performance of a hyper-combustor utilized in turbine based combined cycle engine[J]. Journal of Aerospace Power, 2013, 30(9): 2115-2121. DOI: 10.13224/j.cnki.jasp.2015.09.009 |
| [3] |
郑永煌, 田峰, 李人厚, 等. 基于Petri网的液体火箭发动机启动过程实时在线故障诊断方法[J].
信息与控制, 2010, 39(2): 207-211.
ZHENG Yonghuang, TIAN Feng, LI Renhou, et al. A real time on-line fault diagnosis algorithm based on Petri net for the starting process of liquid propellant rocket engine[J]. Information and Control, 2010, 39(2): 207-211. |
| [4] |
王珺, 张卫红, 石文靓, 等. 60t级LOX/CH4发动机启动过程建模与仿真[J].
火箭推进, 2013, 30(9): 2115-2121.
WANG Jun, ZHANG Weihong, SHI Wenjing, et al. Modeling and simulation of start-up process of 60t class LOX/methane liquid rocket engine[J]. Journal of Rocket Propulsion, 2013, 30(9): 2115-2121. |
| [5] |
鲁峰, 黄金泉, 孔祥天. 涡扇发动机故障诊断的快速模型设计[J].
航空动力学报, 2012, 27(2): 431-437.
LU Feng, HUANG Jinquan, KONG Xiangtian. Rapid prototype design for turbofan engine fault diagnosis[J]. Journal of Aerospace Power, 2012, 27(2): 431-437. DOI: 10.13224/j.cnki.jasp.2012.02.029 |
| [6] |
朱宁, 冯志刚, 王祁. 基于KPCA和SVM的火箭发动机试验台故障诊断方法[J].
哈尔滨工业大学学报, 2009, 41(3): 81-85.
ZHU Ning, FENG Zhigang, WANG Qi. Fault diagnosis of rocket engine ground testing bed based on KPCA and SVM[J]. Journal of Harbin Institute of Technology, 2009, 41(3): 81-85. |
| [7] |
王艳梅, 胡小平, 李舟军. 利用关联规则检测液体火箭发动机启动关机过程的故障[J].
火箭推进, 2006, 32(1): 19-23.
WANG Yanmei, HU Xiaoping, LI Zhoujun. Application of association rules to the fault detection of startingup and shutdown process of liquid rocket engine[J]. Journal of Rocket Propulsion, 2006, 32(1): 19-23. |
| [8] | CABASINO M P, GIUA A, SEATZU C, et al. Fault diagnosis of an ABS system using Petri nets[C]//IEEE International Conference on Automation Science and Engineering. Trieste: IEEE, 2011: 24-27. |
| [9] | CABASINO M P, GIUA A, SEATZU C. Fault detection for discrete event systems using Petri nets with unobserved transitions[J]. Automatica, 2010, 46(9): 1531-1539. DOI: 10.1016/j.automatica.2010.06.013 |
| [10] | CHEN Y F, LI Z W, BARKAOUI K. New Petri nets structure and its application to optimal supervisory control: interval inhibitor arcs[J]. IEEE Transactions on Systems Man and Cybernetics: Systems, 2014, 44(10): 1384-1400. DOI: 10.1109/TSMC.2014.2307284 |
| [11] |
叶丹丹, 罗继亮. 部分可观Petri网结构信息在故障诊断中的应用[J].
控制理论与应用, 2015, 23(3): 366-373.
YE Dandan, LUO Jiliang. Application of structural information of partially observed Petri net in fault diagnosis[J]. Control Theory & Applications, 2015, 23(3): 366-373. DOI: 10.7641/CTA.2015.40510 |
| [12] | BASILE F, CHIACCHIO P, TOMMASI D G. On diagnosability of Petri nets via integer linear programming[J]. Automatica, 2012, 48(9): 2047-2058. DOI: 10.1016/j.automatica.2012.06.039 |
| [13] | BASILE F, CORDONE R, PIRODDI L. A branch and bound approach for the design of decentralized supervisors in Petri net models[J]. Automatica, 2015, 52(7): 322-333. |
| [14] | LEFBVRE D. On-line fault diagnosis with partially observed Petri nets[J]. IEEE Transaction on Automatic Control, 2014, 59(7): 1919-1924. DOI: 10.1109/TAC.2013.2294617 |
| [15] |
刘垠杰, 黄强, 程玉强, 等. 基于动态云BP网络的液体火箭发动机故障诊断方法[J].
航空动力学报, 2012, 27(12): 2842-2849.
LIU Yinjie, HUANG Qiang, CHENG Yuqiang, et al. Fault diagnosis method for liquid-propellant rocket engines based on the dynamic cloud-BP neural network[J]. Journal of Aerospace Power, 2012, 27(12): 2842-2849. DOI: 10.13224/j.cnki.jasp.2012.12.026 |
| [16] | BELIAEV E N, CHEVANOV V K. Mathematical modeling of working processes of liquid propellant rocket engines[M]. Moscow: MIA Publications, 1999. |
 2017, Vol. 49
2017, Vol. 49


