导弹尾翼负载模拟器可在地面半物理仿真中复现飞行环境下尾翼所承受的铰链力矩,用以检测试件在接近真实载荷下的性能,在导弹研发中具有极其重要的作用[1-3].随着导弹技术的发展,新型导弹的机动性能显著提升,意味着尾翼承受的气动力载荷变化更加复杂,要求负载模拟器的快速性、精确性越来越高,传统液压负载模拟器控制性能方面的缺陷日益凸显.随着电力电子技术的发展,电动负载模拟器 (electric dynamic load simulator,EDLS) 得到较广泛的研究[4-6].国外对EDLS研究较少,一般以测功机的形式进行报道[7],国内近年来对EDLS进行了一定程度的研究,但局限于加载力矩较小的应用场合[8],而尾翼承受铰链力矩可达250 N·m,最大角加速度可达8 000 rad/s2,与之对应,EDLS要求较大的加载力矩和较快的响应速度[1],因此其系统结构更为复杂,实现高精度控制的难度较大,具有重要的研究价值.
EDLS是典型的被动式加载系统,影响控制精度的主要原因是来自多余力矩的干扰作用,消除多余力是保障加载精度的基础[2, 9].现有针对EDLS控制设计的研究主要集中在如何抑制或补偿多余力矩,以及与此相结合的控制算法[10-16].这些方法的缺陷要么是加载系统的外回路即力矩回路变化较快,难以进行时标上的分解, 要么是参数整定较繁复,对于较短暂的加载过程,难以保证收敛到全局最优解,无法保障控制效果,要么会引起力矩响应速度的降低, 要么要求加载指令严格满足周期重复性.
实现高精度的力矩加载控制,依赖于对加载力矩的精密测量以及对干扰力矩的有效抑制,此外,控制设计中必须考虑驱动机构及传动机构中的非线性因素.永磁同步电机 (permanent magnet synchronous motors, PMSM) 具有转矩脉动小、调速范围宽等优势,适用于作为EDLS的驱动机构,然而PMSM本身具有非线性强耦合特点[17],此外传动机构中不可避免存在摩擦、参数时变等复杂因素,使得EDLS具有高阶非线性特性.现有文献的不足之处在于均采用基于线性模型的前馈反馈控制结构,忽略了系统中的非线性因素,导致系统逆模型难以精确建立,无法实现多余力矩的精确前馈补偿,难以达到理想的加载精度.
反演控制的优势在于具有处理非匹配不确定的能力,并保证系统的渐进稳定性,虚拟控制量的设计具有高度灵活性,可保证每个子系统的运动品质,体现出独特的细节控制能力,是处理高阶非线性系统的强有力工具[18].滑模控制具有鲁棒性强、工程实现简单等特点,快速终端滑模控制 (fast terminal sliding mode control, FTSMC) 提高了常规滑模控制的收敛速度且具备更高的稳态精度[19],与反演控制相结合可显著提升系统鲁棒性.针对尾翼EDLS的特点,基于反演控制的设计思想,将整体系统划分为3个子系统进行控制设计,采用FTSMC方法设计虚拟控制量,与常规逐层反演控制相比,具有更强的抑制扰动能力,可实现整体系统跟踪误差的有限时间收敛,避免了常规前馈反馈控制结构的若干缺陷,显著提高控制品质.应用Lyapunov方法证明了闭环系统的渐进稳定及有限时间的收敛特性,试验结果表明,本文方法可实现对加载力矩的精确控制.
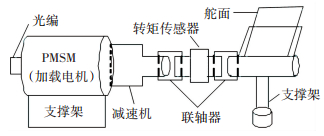
1 系统结构及数学模型导弹尾翼ELDS由伺服电机、减速机构、光电编码器、力矩传感器、加载试件等构成,系统结构如图 1所示.
|
图 1 ELDS系统结构示意 Figure 1 The structure of ELDS |
PMSM作为EDLS的驱动元件,通过联轴器与力矩传感器、减速器、加载试件相连.减速机构及传动机构作为执行元件,转矩传感器实时测量传动机构上的加载力矩,构成力矩反馈回路.
假设磁路不饱和,不计磁滞和涡流损耗影响,气隙磁场呈正弦分布,定子为三相对称绕组,转子无阻尼绕组,隐极式PMSM在d-q坐标系下的电压、转矩和机械方程为[20]
| $ \left\{ \begin{array}{l} {u_d} = {R_{\text{s}}}{i_d} + {L_{\text{s}}}\frac{{{\text{d}}{i_{\text{d}}}}}{{{\text{d}}t}} - {n_{\text{p}}}{\omega _{\text{r}}}{L_{\text{s}}}{i_q}, \hfill \\ {u_q} = {R_{\text{s}}}{i_q} + {L_{\text{s}}}\frac{{{\text{d}}{i_q}}}{{{\text{d}}t}} - {n_{\text{p}}}{\omega _{\text{r}}}\left( {{L_{\text{s}}}{i_d} + {\varphi _{\text{f}}}} \right), \hfill \\ \frac{{{\text{d}}{\omega _{\text{r}}}}}{{{\text{d}}t}} = \frac{1}{J}\left( {{T_{\text{e}}} - {T_{\text{L}}} - B{\omega _{\text{r}}} + {T_0}} \right), \hfill \\ {T_{\text{e}}} = \frac{3}{2}{n_{\text{p}}}{\varphi _{\text{f}}}{i_q}. \hfill \\ \end{array} \right. $ | (1) |
式中:ud、uq分别为PMSM直轴和交轴的电压;id、iq分别为直轴和交轴电流;φf、Rs、Ls分别为永磁体磁链、定子电阻、等效电感;Te为PMSM的电磁转矩;TL为PMSM的负载转矩,即传感器的反馈值;ωr为机构轴系的机械转速;T0为由摩擦、惯性等非线性因素引起的未知非线性力矩,np为PMSM的极对数;B为阻尼系数;J为轴系的转动惯量.
根据胡克定律,传感器的数学模型为
| $ {T_{\text{L}}} = {K_{\text{G}}}\left( {\frac{1}{\tau }\theta - {\theta _{\text{f}}}} \right). $ | (2) |
式中:KG为刚度系数;τ为传动机构减速比;θ为EDLS的角度输出;θf为被加载对象的反馈角度.
对式 (2) 求导并考虑未建模动态误差,与参数不确定因素叠加,视为类似干扰项,则转矩变化率为
| $ {{\dot T}_{\text{L}}} = {K_{\text{G}}}\left( {\frac{1}{\tau }{\omega _{\text{r}}} - {\omega _{\text{f}}}} \right) + {d_1}, $ | (3) |
式中ωf为被加载对象的角速度.
电流环动态特性与电磁转矩直接相关,是衡量加载系统性能的关键指标.随着PMSM运行中绕组温度的变化,电磁特性将发生改变,因此将建模误差及参数时变等视为未知干扰.定义状态变量x =[TL, ωr, iq, id]T,联立式 (1)~(3) 可得基于PMSM的尾翼EDLS系统的数学模型为
| $ \left\{ \begin{array}{l} \frac{{{\text{d}}{T_{\text{L}}}}}{{{\text{d}}t}}{\text{ = }}{K_{\text{G}}}\left( {\frac{1}{\tau }{\omega _{\text{r}}} - {\omega _{\text{f}}}} \right) + {d_1}, \hfill \\ \frac{{{\text{d}}{\omega _{\text{r}}}}}{{{\text{d}}t}} = \frac{1}{J}\left( { - {T_{\text{L}}} - B{\omega _{\text{r}}} + \frac{3}{2}{n_{\text{p}}}{\varphi _{\text{f}}}{i_q}} \right) + {d_2}, \hfill \\ \frac{{{\text{d}}{i_q}}}{{{\text{d}}t}} = - \frac{{{n_{\text{p}}}{\varphi _{\text{f}}}{\omega _{\text{r}}}}}{{{L_{\text{s}}}}} - \frac{{{R_{\text{s}}}}}{{{L_{\text{s}}}}}{i_q} - {n_{\text{p}}}{\omega _{\text{r}}}{i_d} + \frac{1}{{{L_{\text{s}}}}}{u_q} + {d_3}, \hfill \\ \frac{{{\text{d}}{i_{\text{d}}}}}{{{\text{d}}t}} = {n_{\text{p}}}{\omega _{\text{r}}}{i_q} - \frac{{{R_{\text{s}}}}}{{{L_{\text{s}}}}}{i_d} + \frac{1}{{{L_{\text{s}}}}}{u_d} + {d_4}, \hfill \\ y = {T_{\text{L}}}. \hfill \\ \end{array} \right. $ | (4) |
式中:y为系统输出;uq、ud为控制量;di(i=1, …, 4) 为建模误差及参数摄动叠加而成的干扰类似项[21].
根据式 (4) 所描述的非线性多输入输出电动加载系统,由文献[18]可知,该系统可以采用反演控制方法进行控制器设计.
控制目标:对式 (4) 所描述的导弹尾翼EDLS系统设计控制器,实现对期望力矩信号TL*(t) 的跟踪,实现跟踪误差有限时间内收敛到零.
假设1 TL*(t) 连续,一阶导数一致连续且有界.
假设2 di (i=1, 2, 3, 4) 皆有界,连续可微且满足Lipschitz条件,即存在正实数ρi使
根据EDLS的结构和功能,将整体系统划分为负载转矩子系统,PMSM的机械子系统以及电气子系统.首先分析EDLS的负载转矩子系统,控制任务是设计控制量ωr*,使得TL在有限时间内实现对TL*的无静差跟踪. ωr*既是力矩子系统的控制输入信号,也是转速子系统的参考信号,因此需要消除抖振,避免由于对控制切换项中符号函数求导引起转速子系统控制器奇异.根据相对阶理论可知,负载转矩子系统相对阶为1,因此需要设计阶数大于1的滑模控制器,可实现无抖振控制,保证ωr平滑[22].从控制性能考虑,常规线性滑模面具有指数渐进收敛特性,在有限时间内必然存在控制误差,采用终端滑模控制,实现有限时间内跟踪误差收敛,对于提高力矩加载精度具有重要意义.从以上两方面考虑,设计无抖振的快速终端滑模控制器最为理想.
设误差变量z1=TL-TL*,设计终端滑模面[23]为
| $ {s_1} = {{\dot z}_1} + {\alpha _1}{z_1} + {\beta _1}{z_1}^{{q_0} \cdot p_0^{ - 1}}. $ | (5) |
式中α1、β1为正实数,q0、p0为奇数且满足p0 > q0.
由式 (5) 可知,当z1远离零点时有s1≈ż1+α1z1,此时为近似指数收敛,若z1靠近零点时,s1≈ż1+β1z1q0·p-10,此时Terminal吸引子起主要作用,对β1z1q0·p-10的合理设计可显著加快系统靠近平衡点阶段的收敛速度.可知该方法具有常规Terminal滑模控制有限时间收敛的特点,又具有起始阶段收敛速度快的优势.设计虚拟控制量ωr*为
| $ \left\{ \begin{array}{l} \omega _{\text{r}}^ * = \tau K_{\text{G}}^{ - 1}\left( {\omega _{{\text{req}}}^ * + \omega _{{\text{rsw}}}^ * } \right), \hfill \\ \omega _{{\text{req}}}^ * = {K_{\text{G}}}{\omega _{\text{f}}} + \dot T_{\text{L}}^ * - {\alpha _1}{z_1} - {\beta _1}{z_1}^{{q_0} \cdot p_0^{ - 1}}, \hfill \\ \omega _{{\text{rsw}}}^ * = - \int_0^t {\left( {{\kappa _1}{s_1} + {\gamma _1}s_1^{q \cdot {p^{ - 1}}}} \right){\text{d}}t} . \hfill \\ \end{array} \right. $ | (6) |
式中:KG-1ωreq*为等效控制项;KG-1ωrsw*为切换控制项;q、p为奇数, 且满足p > q.
由于将控制项隐藏在积分表达式中,使得虚拟控制量连续可微.由式 (6) 可知,等效控制中含有被加载对象的信息 (运动角速度ωf),与文献[6]中的前馈补偿相比,该控制设计中已充分考虑被加载对象运动产生的多余力矩,保证多余力矩的有效抑制,与基于线性输入输出模型的补偿控制设计相比,更充分地利用系统信息,体现出非线性控制的优越性.对式 (6) 求微分,并将式 (4) 代入可得
| $ \begin{array}{l} {{\dot s}_1} = {{\ddot z}_1} + {\alpha _1}{{\dot z}_1} + {\beta _1}\frac{d}{{{\text{d}}t}}{z_1}^{{q_0} \cdot p_0^{ - 1}} = {K_{\text{G}}}{{\dot \omega }_{\text{r}}} - {K_{\text{G}}}{{\dot \omega }_{\text{f}}} + \hfill \\ \;\;\;\;\;\;{{\dot d}_1} - \ddot T_{\text{L}}^ * + {\alpha _1}{{\dot z}_1} + {\beta _1}\frac{d}{{{\text{d}}t}}{z_1}^{{q_0} \cdot p_0^{ - 1}}. \hfill \\ \end{array} $ | (7) |
将式 (6) 代入式 (7),可简化为
| $ {{\dot s}_1} = - {\kappa _1}{s_1} - {\gamma _{11}}s_1^{q \cdot {p^{ - 1}}} - {\gamma _{12}}s_1^{q \cdot {p^{ - 1}}} + {{\dot d}_1}. $ | (8) |
式中γ11+γ12=γ1.选取Lyapunov函数:
| $ {V_1} = \frac{1}{2}s_1^2, $ | (9) |
对式 (9) 求导,将式 (8) 代入式 (9),结合假设2可得
| $ \begin{array}{l} {{\dot V}_1} = {s_1}{{\dot s}_1} \leqslant {s_1}\left( { - {\kappa _1}{s_1} - {\gamma _{11}}s_1^{q \cdot {p^{ - 1}}} - {\gamma _{12}}s_1^{q \cdot {p^{ - 1}}} + {{\dot d}_1}} \right) \leqslant \hfill \\ \;\;\;\;\;\; - {\kappa _1}s_1^2 - {\gamma _{11}}s_1^{\left( {q + p} \right) \cdot {p^{ - 1}}} - {\gamma _{12}}s_1^{\left( {q + p} \right) \cdot {p^{ - 1}}} + {s_1}\left| {{\rho _1}} \right|. \hfill \\ \end{array} $ | (10) |
取γ12≥ρ1/s1q·p-1,有
分析PMSM的机械部分,控制任务是设计控制量iq*,使ωr在有限时间内对ωr*实现良好跟踪.与负载转矩子系统设计方法相似,定义误差变量z2=ωr-ωr*,设计滑模面为
| $ {s_2} = {{\dot z}_2} + {\alpha _2}{z_2} + {\beta _2}{z_2}^{{q_0} \cdot p_0^{ - 1}}. $ | (11) |
与2.1控制器设计类似,设置α2、β2为正实数,q0、p0为奇数,且满足p0 > q0.取虚拟控制量iq*为
| $ \left\{ \begin{array}{l} i_q^ * = \frac{{2J}}{{3{n_{\text{p}}}{\varphi _{\text{f}}}}}\left( {i_{{\text{qeq}}}^ * + i_{{\text{qsw}}}^ * } \right), \hfill \\ i_{{\text{qeq}}}^ * = {J^{ - 1}}\left( {{T_{\text{L}}} + B{\omega _{\text{r}}}} \right) + \dot \omega _{\text{r}}^ * - {\alpha _2}{z_2} - {\beta _2}{z_2}^{{q_0} \cdot p_0^{ - 1}}, \hfill \\ i_{{\text{qsw}}}^ * = - \int_0^t {\left( {{\kappa _2}{s_2} + {\gamma _2}s_2^{q \cdot {p^{ - 1}}}} \right){\text{d}}t} . \hfill \\ \end{array} \right. $ | (12) |
式中
对式 (12) 求微分,将式 (4) 代入可得
| $ \begin{array}{l} {{\dot s}_2} = {{\ddot z}_2} + {\alpha _2}{{\dot z}_2} + {\beta _2}\frac{d}{{{\text{d}}t}}{z_2}^{{q_0} \cdot p_0^{ - 1}} = \hfill \\ \;\;\;\;\;\;\frac{1}{J}\left( { - {{\dot T}_{\text{L}}} - B{{\dot \omega }_{\text{r}}} + \frac{3}{2}{n_{\text{p}}}{\varphi _{\text{f}}}{{\dot i}_{\text{q}}}} \right) - \hfill \\ \;\;\;\;\;\;\ddot \omega _{\text{r}}^ * + {{\dot d}_2} + {\alpha _2}{{\dot z}_2} + {\beta _2}\frac{d}{{{\text{d}}t}}{z_2}^{{q_0} \cdot p_0^{ - 1}}. \hfill \\ \end{array} $ | (13) |
将式 (12) 代入式 (13),可得
| $ {{\dot s}_2} = - {\kappa _2}{s_2} - {\gamma _2}s_2^{q \cdot {p^{ - 1}}} + {{\dot d}_2}. $ | (14) |
选取Lyapunov函数:
| $ {V_2} = {V_1} + \frac{1}{2}s_2^2. $ | (15) |
对式 (15) 求导,并将式 (10)~(14) 代入得
| $ \begin{array}{l} {{\dot V}_2} = {V_1} + {s_2}{{\dot s}_2} \leqslant - \sum\limits_{i = 1}^2 {\left( {{\kappa _i}s_i^2 - {\gamma _{i1}}s_i^{\left( {q + p} \right) \cdot {p^{ - 1}}} - } \right.} \hfill \\ \left. {{\gamma _{i2}}s_i^{\left( {q + p} \right) \cdot {p^{ - 1}}} + {s_i}\left| {{\rho _i}} \right|} \right). \hfill \\ \end{array} $ | (16) |
式中γ2=γ21+γ22,取γ22≥ρ2(|s2q·p-1|)-1,则
分析PMSM的电气子系统,设计交轴电流控制器,使得交轴电流iq可精确跟踪参考电流值iq*.为实现电流和速度的解耦,使转矩不受磁通电流的影响,采用id*=0的控制策略,使直轴电流控制器设计大为简化,定义误差变量z3=iq-iq*,z4=id-id*,设计滑模面为
| $ \left\{ \begin{array}{l} {s_3} = {{\dot z}_3} + {\alpha _3}{z_3} + {\beta _3}{z_3}^{{q_0} \cdot p_0^{ - 1}}, \hfill \\ {s_4} = {{\dot z}_4} + {\alpha _4}{z_4} + {\beta _4}{z_4}^{{q_0} \cdot p_0^{ - 1}}. \hfill \\ \end{array} \right. $ | (17) |
设计交轴电压uq为等效控制uqeq与鲁棒控制项uqsw的叠加形式为
| $ \left\{ \begin{array}{l} {u_q} = {L_{\text{s}}}\left( {{u_{{\text{qeq}}}} + {u_{{\text{qsw}}}}} \right), \hfill \\ {u_{{\text{qeq}}}} = \frac{{{R_{\text{s}}}{i_q}}}{{{L_{\text{s}}}}} + {n_{\text{p}}}{\omega _{\text{r}}}{i_d} + \frac{{{n_{\text{p}}}{\varphi _{\text{f}}}{\omega _{\text{r}}}}}{{{L_{\text{s}}}}} + \hfill \\ \;\;\;\;\;\;\;\;\;\dot i_q^ * - {\alpha _3}{z_3} - {\beta _3}{z_3}^{{q_0} \cdot p_0^{ - 1}}, \hfill \\ {u_{{\text{qsw}}}} = - \int_0^t {\left( {{\kappa _3}{s_3} + {\gamma _3}s_3^{q \cdot {p^{ - 1}}}} \right){\text{d}}t} . \hfill \\ \end{array} \right. $ | (18) |
设计直轴电压ud为
| $ \left\{ \begin{array}{l} {u_d} = {L_{\text{s}}}\left( {{u_{{\text{deq}}}} + {u_{{\text{dsw}}}}} \right), \hfill \\ {u_{{\text{deq}}}} = \frac{{{R_{\text{s}}}}}{{{L_{\text{s}}}}}{i_d} - {n_{\text{p}}}{\omega _{\text{r}}}{i_q} - {\alpha _4}{z_4} + {\beta _4}{z_4}^{{q_0} \cdot p_0^{ - 1}}, \hfill \\ {u_{{\text{dsw}}}} = - \int_0^t {\left( {{\kappa _4}{s_4} + {\gamma _4}s_4^{q \cdot {p^{ - 1}}}} \right){\text{d}}t} . \hfill \\ \end{array} \right. $ | (19) |
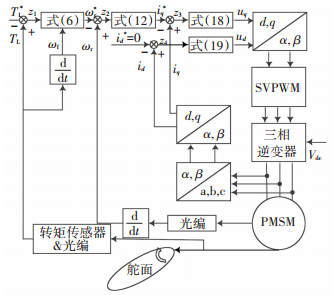
由式 (18)、(19) 可知,实际控制量uq、ud为连续可微函数,消除了常规滑模控制存在的抖振.综上所述,尾翼EDLS系统的FTSMC结构如图 2所示.
|
图 2 导弹尾翼EDLS系统FTSMC控制 Figure 2 The control structure of EDLS with FTSMC |
引理1 若a1, a2, …, an及δ∈ (0, 2) 皆为正实数,则以下不等式成立[24].
| $ {\left| {{a_1}} \right|^\delta } + {\left| {{a_2}} \right|^\delta } + \cdots + {\left| {{a_n}} \right|^\delta } \geqslant {\left( {a_1^2 + a_2^2 + \cdots + a_n^2} \right)^{0.5\delta }}. $ | (20) |
引理2 若连续可微Lyapunov函数V(t) 满足如下不等式.
| $ \dot V\left( t \right) \leqslant - \alpha V\left( t \right) - \beta {V^\gamma }\left( t \right),\;\;\;\;\forall t \geqslant {t_0}. $ | (21) |
式中α, β>0,0<γ<1,则V(t) 可在有限时间内收敛到零点,收敛时间为[25]
| $ {t_1} \leqslant {t_0} + \frac{1}{{\alpha \left( {1 - \gamma } \right)}}\ln \frac{{\alpha {V^{1 - \gamma }}\left( {{t_0}} \right) + \beta }}{\beta }. $ | (22) |
定理1 对式 (4) 所示含导弹尾翼EDLS系统,虚拟控制量设计如式 (6)、(12),采用式 (18)、(19) 所示交轴直轴电流控制律,若满足假设1、假设2,取适当的滑模面参数q0、p0、αi、βi及控制器参数κi、γi(i=1, 2, 3, 4),则滑模面si有限时间内可达,跟踪误差随后在有限时间内收敛为零.
证明 对式 (17) 求导,并将式 (4)、(18)~(19) 代入可得
| $ \begin{array}{l} {{\dot s}_3} = {{\ddot i}_q} - \ddot i_q^ * + {\alpha _3}{{\dot z}_3} + {\beta _3}\frac{{\text{d}}}{{{\text{d}}t}}z_3^{{q_0} \cdot p_0^{ - 1}} = \hfill \\ \;\;\;\;\;\;\frac{{\text{d}}}{{{\text{d}}t}}\left( { - \frac{{{n_{\text{p}}}{\omega _{\text{f}}}{\omega _{\text{r}}}}}{{{L_{\text{s}}}}} - \frac{{{R_{\text{s}}}}}{{{L_{\text{s}}}}}{i_q} - {n_{\text{p}}}{\omega _{\text{r}}}{i_d}} \right) + \frac{{{{\dot u}_q}}}{{{L_{\text{s}}}}} + {{\dot d}_3} + {\alpha _3}{{\dot z}_3} + \hfill \\ \;\;\;\;\;\;{\beta _3}\frac{{\text{d}}}{{{\text{d}}t}}z_3^{{q_0} \cdot p_0^{ - 1}} = - {\kappa _3}{s_3} - {\gamma _3}s_3^{q \cdot {p^{ - 1}}} + {{\dot d}_3}. \hfill \\ \end{array} $ | (23) |
| $ \begin{array}{l} {{\dot s}_4} = {{\ddot i}_d} + {\alpha _4}{{\dot z}_4} + {\beta _4}\frac{{\text{d}}}{{{\text{d}}t}}z_4^{{q_0} \cdot p_0^{ - 1}} = \frac{{\text{d}}}{{{\text{d}}t}}\left( {{n_{\text{p}}}{\omega _{\text{r}}}{i_q} - \frac{{{R_{\text{s}}}}}{{{L_{\text{s}}}}}{i_d}} \right) + \hfill \\ \frac{{{{\dot u}_d}}}{{{L_{\text{s}}}}} + {{\dot d}_4} + {\alpha _4}{{\dot z}_4} + {\beta _4}\frac{{\text{d}}}{{{\text{d}}t}}z_4^{{q_0} \cdot p_0^{ - 1}} = - {\kappa _4}{s_4} - {\gamma _4}s_4^{q \cdot {p^{ - 1}}} + {{\dot d}_4}. \hfill \\ \end{array} $ | (24) |
选取整体系统的控制Lyapunov函数:
| $ V = {V_2} + \frac{1}{2}s_3^2 + \frac{1}{2}s_4^2. $ | (25) |
对式 (25) 求微分,并将式 (16)、(23)、(24) 代入得
| $ \begin{array}{l} \dot V = \sum\limits_{i = 1}^4 {{s_i}{{\dot s}_i}} = - \sum\limits_{i = 1}^4 {{\kappa _i}s_i^2} - \sum\limits_{i = 1}^2 {{\gamma _{i1}}s_i^{\left( {q + p} \right) \cdot {p^{ - 1}}}} - \hfill \\ \;\;\;\;\;{\gamma _3}s_3^{\left( {q + p} \right) \cdot {p^{ - 1}}} + {{\dot d}_3}{s_3} - {\gamma _4}s_4^{\left( {q + p} \right) \cdot {p^{ - 1}}} + {{\dot d}_4}{s_4} \leqslant \hfill \\ \;\;\;\;\; - \sum\limits_{i = 1}^4 {{\kappa _i}s_i^2} - \sum\limits_{i = 1}^2 {{\gamma _{i1}}s_i^{\left( {q + p} \right) \cdot {p^{ - 1}}}} - {\gamma _{32}}s_3^{\left( {q + p} \right) \cdot {p^{ - 1}}} + \hfill \\ \;\;\;\;\;{{\dot d}_3}{s_3} - {\gamma _{42}}s_4^{\left( {q + p} \right) \cdot {p^{ - 1}}} + {{\dot d}_4}{s_4}. \hfill \\ \end{array} $ | (26) |
式中γ3=γ31+γ32,γ4=γ41+γ42.
由假设2可得
| $ \begin{array}{l} \dot V \leqslant - \sum\limits_{i = 1}^4 {{\kappa _i}s_i^2} - \sum\limits_{i = 1}^4 {{\gamma _{i1}}s_i^{\left( {q + p} \right) \cdot {p^{ - 1}}}} - {\gamma _{32}}s_3^{\left( {q + p} \right) \cdot {p^{ - 1}}} + \hfill \\ \;\;\;\;\;\;\;{\rho _3}\left| {{s_3}} \right| - {\gamma _{42}}s_4^{\left( {q + p} \right) \cdot {p^{ - 1}}} + {\rho _4}\left| {{s_4}} \right|. \hfill \\ \end{array} $ | (27) |
取γ32≥ρ3/|s3q·p-1|,γ42≥ρ4/|s4q·p-1|,则有
| $ \begin{array}{l} \dot V \leqslant - \sum\limits_{i = 1}^4 {{\kappa _i}s_i^2} - \sum\limits_{i = 1}^4 {{\gamma _{i1}}s_i^{\left( {q + p} \right) \cdot {p^{ - 1}}}} \leqslant \hfill \\ \;\;\;\;\;\;\; - \bar \kappa \sum\limits_{i = 1}^4 {s_i^2} - \bar \gamma \sum\limits_{i = 1}^4 {s_i^{\left( {q + p} \right) \cdot {p^{ - 1}}}} . \hfill \\ \end{array} $ | (28) |
由q+p为偶数有s(q+p)·pi-1≥0,由引理1可知
| $ \sum\limits_{i = 1}^4 {s_i^{\left( {q + p} \right) \cdot {p^{ - 1}}}} \geqslant \sum\limits_{i = 1}^4 {{{\left( {s_i^2} \right)}^{\left( {q + p} \right) \cdot {{\left( {2p} \right)}^{ - 1}}}}} , $ | (29) |
则式 (28) 可化为
| $ \dot V \leqslant - 2\bar \kappa V - {2^{\left( {q + p} \right) \cdot {{\left( {2p} \right)}^{ - 1}}}}\bar \gamma {V^{\left( {q + p} \right) \cdot {{\left( {2p} \right)}^{ - 1}}}}. $ | (30) |
由引理2可知,V(t) 可在有限时间t1内收敛到零,t1表达式为
| $ {t_1} = \frac{p}{{\bar \kappa \left( {p - q} \right)}}\ln \left( {\frac{{2\bar \kappa V{{\left( {{t_0}} \right)}^{\left( {p - q} \right) \cdot {{\left( {2p} \right)}^{ - 1}}}} + {2^{\left( {q + p} \right) \cdot {{\left( {2p} \right)}^{ - 1}}}}\bar \gamma }}{{{2^{\left( {q + p} \right) \cdot {{\left( {2p} \right)}^{ - 1}}}}\bar \gamma }}} \right). $ |
结合终端滑模面性质,可知跟踪误差随后在有限时间收敛为零.本文设计的控制器有如下特点:1) 增大κ可显著缩短滑模面到达时间,但κ本质上是切换控制项增益,过大的κ会导致控制器输出震荡,应合理设置以达到收敛速度与控制性能的均衡. 2) 虚拟控制量设计中采用无抖振终端滑模控制,将非匹配不确定转化为匹配不确定,利用滑模控制方法设计干扰抑制项,使得系统具备更强的鲁棒性. 3) 采用文献[22]提出的有限时间微分估计器方法计算
为验证本文方法的有效性,在自行研制的负载模拟器上进行力矩加载试验,试验平台如图 3所示.导弹尾翼真实展开的动力源是火工品,为模拟尾翼展开过程中能量冲击作用,设计液压冲击模拟器.系统开始工作时由蓄能器向油泵补高压油,通过压力传感器实时监测油压,达到设定压力后关闭油泵,采用高压油推动油缸完成作动过程.

|
图 3 导弹尾翼ELDS实验平台 Figure 3 The test platform of EDLS |
加载使用的电机为自行研制的PMSM,控制器选用DSP320F28335. PMSM具体参数如下:额定电磁转矩Te*=27.3 N·m,磁极对数np=4,粘滞系数B=2.0×10-4 N·m/(rad/s),转子磁链φf=0.111 9 Wb,转动惯量J=1.6×10-3 kg·m2,定子电阻Rs=0.11 Ω,绕组电感Ls=0.97 H,直流母线电压Vdc=560 V.采用自行设计的力矩传感器,测量范围为-500~500 N·m,测量精度为0.03%,刚度系数KG为6 000 N·m/rad.传动机构减速比τ=10.
3.2 试验结果及分析采用本文方法设计控制器,滑模面参数设置为:α1=α2=4,α3=α4=2,β1=β2=6,β3=β4=3,q0/p0= 3/7;控制器参数设置为:κ1=κ2=10,κ3=κ4=6,γ1=γ2=5,γ3=γ4=3,q/p=1/3.为验证本文方法的有效性,分别采用本文方法和常规PI+前馈补偿两种方法进行试验,PI+前馈补偿采用三闭环控制,即电流环、速度环和力矩环,前馈采用直接前馈法,经调试确定其参数分别为:电流环q轴电流PI为kp=5, kI=0.005,d轴电流PI为kp=6,ki=0.04;速度环kp=8,kI=0.2;力矩环kp=2,kI=1.05,kd=0.001;前馈补偿增益为减速比值,即k=10.试验过程控制量和状态变量的初始值设定均为0.
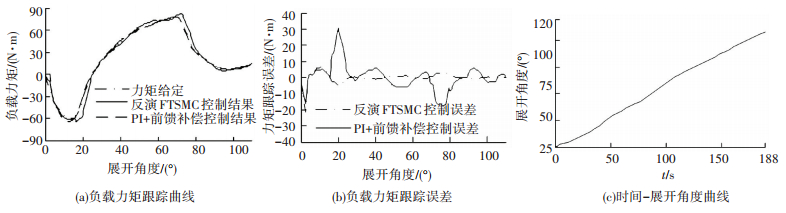
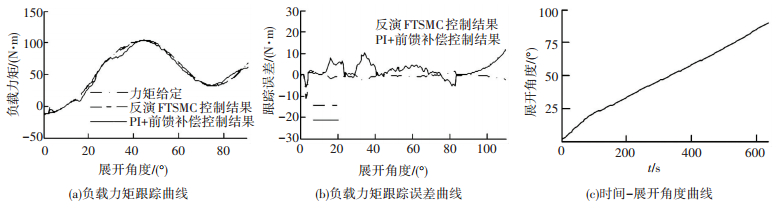
试验分别模拟导弹尾翼快速展开110°、90°两种工况下的负载力矩,力矩给定表示导弹尾翼在展开过程中所受到的铰链力矩,结果如图 4、5所示.
|
图 4 尾翼展开110°试验结果 Figure 4 Experimental results of missile rudder with 110° |
|
图 5 尾翼展开90°试验结果 Figure 5 Experimental results of missile rudder with 90° |
图 4为最大加载力矩80 N·m条件下试验结果,图 4(a)为展开角度-加载力矩响应曲线,图 4(b)为力矩跟踪误差,图 4(c)为尾翼展开角度随时间的变化曲线.可以看出,反演FTSMC控制方法最大力矩跟踪误差是在初始时刻的17 N·m,随着尾翼的展开,力矩跟踪误差迅速收敛,尾翼展开到20°以后 (时间为24 ms),力矩误差小于4 N·m,力矩跟踪精度受力矩给定及尾翼展开速度变化的影响较小,抗干扰能力强. PID+前馈补偿方法的初始力矩误差为22 N·m,最大误差为30 N·m,在展开角30°之后大部分力矩误差小于10 N·m,当展开角度到70°,此时给定力矩发生突变,PID+前馈补偿方法的跟踪误差达到18 N·m,与反演FTSMC控制方法相比,PID+前馈补偿的抗干扰性和鲁棒性较差.
图 5为所示为导弹尾翼在展开角度为90°,最大负载力矩为100 N·m的工况下,本文方法与PI+前馈补偿两种方法的试验结果,与尾翼展开110°工况类似.展开110°时,PI+前馈补偿的最大误差为30 N·m,稳态误差小于10 N·m,本文方法的最大误差为17 N·m,稳态误差小于5 N·m;展开角度为90°时,PI+前馈补偿的最大误差为10 N·m,稳态误差小于5 N·m,本文方法的最大误差为5 N·m,稳态误差小于3 N·m的力矩误差.表明110°展开试验的力矩误差大于90°展开试验,这是由于尾翼展开角度110°试验中,展开时间为188 ms,而展开90°所用时间大于600 ms,即展开时间越短,尾翼的速度及加速度变化越剧烈,导致加载系统中多余力矩越大,控制也越困难,因而控制误差相对较大.与常规PI+前馈补偿控制方法相比,快速终端滑模控制能够更好地抑制多余力矩对系统的影响,力矩加载误差小,抗干扰能力强,鲁棒性好,力矩加载控制精度更为理想.
4 结论1) 针对永磁同步电机驱动的导弹尾翼电动负载模拟器存在的多余力矩、参数时变及未知扰动,基于反演控制思想,设计了一种快速终端滑模控制器.
2) 克服了现有文献控制设计中存在的若干不足,利用终端滑模有限时间收敛的优势设计控制律,证明了滑模面有限时间可达及系统跟踪误差有限时间收敛性.试验结果验证了控制算法的有效性.
3) 利用反演思想设计滑模控制器可弥补常规反演或动态面控制的若干缺陷,适用于ELDS系统控制器设计,与高阶滑模控制器相比,避免了精确线性化过程高度依赖模型精度的困难.
4) 考虑驱动电机本身的非线性因素,设计快速终端滑模控制得到连续的电流控制律,并分析了影响力矩加载精度及误差收敛时间的若干因素,避免了常规滑模控制存在的抖振问题,提高系统鲁棒性.
| [1] |
齐蓉, 林辉. 弹翼电动加载系统多余力矩分析与消除[J].
西北工业大学学报, 2005, 23(6): 759-763.
QI Rong, LIN Hui. Analysis and elimination of surplus torque in missile wing electric loading system[J]. Journal of Northwestern Polytechnical University, 2005, 23(6): 759-763. |
| [2] |
齐蓉, 林辉, 陈明. 被动式电动加载系统多余力的研究[J].
控制与决策, 2006, 21(2): 225-228.
QI Rong, LIN Hui, CHEN Ming. Research on surplus torque in passive electric loading system[J]. Control and Design, 2006, 21(2): 225-228. |
| [3] |
汪首坤, 王军政. 导弹舵机动态加载技术[J].
北京理工大学学报, 2007, 27(3): 247-250.
WANG Shoukun, WANG Junzheng. Dynamic loading for missile actuators[J]. Transactions of Beijing Institute of Technology, 2007, 27(3): 247-250. |
| [4] | AKPOLAT Z H. Dynamic emulation of mechanical loads using a vector-controlled induction motor-generator set[J]. IEEE Transactions on Industrial Electronics, 1999, 46(2): 370-379. DOI: 10.1109/41.753776 |
| [5] | ARELLANO-PADILLA J, ASHER G M, SUMNER M. Control of an AC dynamometer for dynamic emulation of mechanical loads with stiff and flexible shafts[J]. IEEE Transactions on Industrial Electronics, 2006, 53(4): 1250-1260. DOI: 10.1109/TIE.2006.878309 |
| [6] |
李成功, 靳红涛, 焦宗夏. 电动负载模拟器多余力矩产生机理及抑制[J].
北京航空航天大学学报, 2006, 32(2): 204-208.
LI Chenggong, JIN Hongtao, JIAO Zongxia. Mechanism and suppression of extraneous torque of motor driver load simulator[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(2): 204-208. |
| [7] | AKPOLAT Z H, ASHER G M, CLARE J C. Experimental dynamometer emulation of nonlinear mechanical loads[J]. IEEE Transactions on Industry Applications, 1999, 35(6): 1367-1373. DOI: 10.1109/28.806051 |
| [8] |
杨波, 王俊奎. 无人机舵面负载模拟系统的小脑模型控制[J].
北京航空航天大学学报, 2009, 35(11): 1361-1365.
YANG Bo, WANG Junkui. CMAC neural network for the rudder dynamic load simulator of unmanned aerial vehicles[J]. Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(11): 1361-1365. |
| [9] |
杨波, 程龙. 提高电动加载系统输出平滑的CMAC复合控制[J].
北京航空航天大学学报, 2013, 39(6): 723-727.
YANG Bo, CHENG Long. Improving the output smoothing of the electric loading system based on the CMAC+PD compound control strategy[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(6): 723-727. |
| [10] | YAO J Y, JIAO Z X, YAO B. Nonlinear adaptive robust backstepping force control of hydraulic load simulator: Theory and experiments[J]. Journal of Mechanical Science and Technology, 2014, 28(4): 1499-1507. DOI: 10.1007/s12206-014-0137-z |
| [11] |
方强, 姚郁. 电动负载模拟器扰动观测器系统化设计[J].
哈尔滨工业大学学报, 2007, 39(3): 349-353.
FANG Qiang, YAO Yu. A systemic disturbance observer design for EALS[J]. Journal of Harbin Institute of Technology, 2007, 39(3): 349-353. |
| [12] |
杨波, 王俊奎. 基于改进的CMAC的电动加载系统复合控制[J].
航空学报, 2008, 29(5): 1314-1318.
YANG Bo, WANG Junkui. Hybrid Control based on improved CMAC for motor-driven loading system[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(5): 1314-1318. |
| [13] |
陈康, 黄勇, 孙力. 电动直线舵机方波加载系统研究[J].
宇航学报, 2008, 29(5): 1515-1520.
CHEN Kang, HUANG Yong, SUN Li. The research of linear rudder square-direction electric loading system[J]. Journal of Astronautics, 2008, 29(5): 1515-1520. |
| [14] |
沈东凯, 华清, 王占林. 基于神经网络的电动加载系统[J].
航空学报, 2002, 23(6): 525-529.
SHEN Dongkai, HUA Qing, WANG Zhanlin. Motor-driven load system based on neural networks[J]. Acta Aeronautica et Astronautica Sinica, 2002, 23(6): 525-529. |
| [15] |
王鑫, 冯冬竹. 引入弹簧杆的电动负载模拟器实验研究[J].
电机与控制学报, 2012, 16(9): 91-94.
WANG Xin, FENG Dongzhu. Experimental research on DC load simulator test bed with elastic rod[J]. Electric Machines and Control, 2012, 16(9): 91-94. |
| [16] |
牛国臣, 王巍, 宗光华. 基于迭代学习的电动负载模拟器复合控制[J].
控制理论与应用, 2014, 31(12): 1740-1747.
NIU Guochen, WANG Wei, ZONG Guanghua. Composite control for electric load simulator based on iterative learning[J]. Control Theory & Applications, 2014, 31(12): 1740-1747. |
| [17] | LEE J S, LORENZ R D, VALENZUELA M A. Time-optimal and loss-minimizing deadbeat-direct torque and flux control for interior permanent-magnet synchronous machines[J]. IEEE Transactions on Industry Applications, 2014, 50(3): 1880-1890. DOI: 10.1109/TIA.2013.2287313 |
| [18] | KRSTIC M, KANELLAKOPOULOS I, KOKOTOVIC P. Nonlinear and adaptive control design[M]. New York: Wiley Interscience, 1995. |
| [19] | QI Liang, SHI Hongbo. Adaptive position tracking control of permanent magnet synchronous motor based on RBF fast terminal sliding mode control[J]. Neurocomputing, 2013, 115(4): 23-30. |
| [20] | YU Jinpeng, SHI Peng, DONG Wenjie, et al. Neural network-based adaptive dynamic surface control for permanent magnet synchronous motors[J]. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(3): 640-645. DOI: 10.1109/TNNLS.2014.2316289 |
| [21] | WEN Changyun, ZHOU Jing, LIU Zhitao, et al. Robust adaptive control of uncertain nonlinear systems in the presence of input saturation and external disturbance[J]. IEEE Transactions on Automatic Control, 2011, 56(7): 1672-1678. DOI: 10.1109/TAC.2011.2122730 |
| [22] | LEVANT A. Chattering analysis[J]. IEEE Transactions on Automatic Control, 2010, 55(6): 1380-1389. DOI: 10.1109/TAC.2010.2041973 |
| [23] | XU S S, CHEN C, WU Z. Study of nonsingular fast terminal sliding-mode fault-tolerant control[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3906-3913. |
| [24] | YU Shuanghe, YU Xinghuo, SHIRINZADEH B, et al. Continuous finite-time control for robotic manipulators with terminal sliding mode[J]. Automatica, 2005, 41(11): 1957-1964. DOI: 10.1016/j.automatica.2005.07.001 |
| [25] | NEKOUKAR V, ERFANIAN A. Adaptive fuzzy terminal sliding mode control for a class of MIMO uncertain nonlinear systems[J]. Fuzzy Sets and Systems, 2011, 179(1): 34-49. DOI: 10.1016/j.fss.2011.05.009 |
 2017, Vol. 49
2017, Vol. 49


