光谱成像技术是一种集合了光谱技术和成像技术的多维信息获取和处理技术,在获得待测目标二维空间信息的同时,可以获得二维空间每一个点元的光谱信息,实现了“图谱合一”[1-2].由于其优越的信息获取能力,光谱成像技术在航天遥感、资源勘探、环境与灾害监测、医学诊断及军事等领域越来越具有不可替代的地位和应用价值.
快照式傅里叶成像光谱技术[3-4],相对扫描式成像光谱技术,可在一个积分时间内获得完整的三维数据集,无需扫描部件或滤波器,可对快变目标进行测量,具有误差小、稳定性好、结构简单,实时性强等优点,在实时侦测等方面具有巨大发展潜力.
相对于扫描式的成像光谱仪,目前快照式傅里叶变换成像光谱仪的实时性仅体现在获取图像信息实时上,通过获取的图像信息恢复出三维“空间-光谱”数据立方体的时间通常较长,很难真正的应用于实时监测中.目前也没有文献针对快照傅里叶成像光谱仪的提出快速光谱重构方法.
近些年来,随着大规模并行计算的发展,GPU凭借着其强大的并行处理能力、高性价比以及低功耗等诸多优点,在高性能计算领域逐渐成为研究热点[5-7].在光谱成像领域,光谱数据量一般较大,利用GPU并行计算的优势,通过尽可能地将算法中可并行部分移交给GPU处理,可大幅度提高处理效率.近几年来GPU正逐渐应用于光谱图像混合像元分解[8],目标探测与分类[9-11],高光谱图像压缩[12],傅里叶变换光谱复原[13]等诸多方面.本文通过分析快照式傅里叶成像光谱仪的工作原理和数据特性,结合CUDA并行计算架构,对复原算法进行了改进,实现了并行化的光谱重构,提高了光谱复原效率,为真正的“实时”测量作了铺垫.
1 快照式成像光谱仪工作原理本文研究的快照式成像光谱仪[14],采用基于双折射晶体干涉仪的空间调制方式,通过改变光传输介质折射率的方式产生光程差.采用快照的方式进行干涉信息获取,利用微透镜阵列进行孔径分割,在一个快门的时间内获取待测目标的完整干涉图像,其系统结构如图 1所示[2].
|
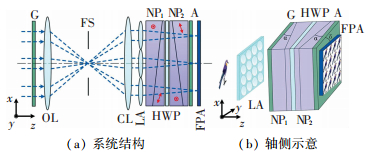
图 1 系统结构示意 Figure 1 Schematic diagram of system structure |
来自目标物的光线经过起偏器G后由物镜OL成像至光阑FS,再经由准直镜CL准直,准直后的入射光经过M×N微透镜阵列LA,目标物图像被复制为M×N个,复制的图像在成像过程中会经过由两块诺瓦斯基棱镜 (NP1,NP2)、半波片HWP以及检偏器A组成的双折射晶体干涉仪,最终成像于探测器FPA上.其中,G的透光轴方向与x轴成45°(沿z轴正方向,逆时针方向为正),经过G后入射光变为偏振方向沿G透光轴方向的线偏振光.诺瓦斯基棱镜NPs的光轴方向如图 1(a)所示,根据双折射晶体的特性,入射光将被分为两个偏振方向相互垂直的分量,由于双折射晶体的寻常光 (o光) 和非寻常光 (e光) 折射率不同,两偏振分量间将产生光程差OPD,OPD的大小沿棱镜光楔厚度变化最快方向变化.
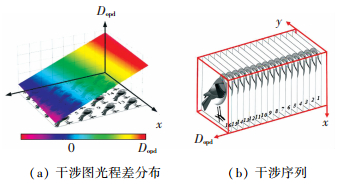
如果将由NPs、HWP和A构成的双折射干涉仪绕z轴旋转δ角,如图 1(b)所示,合适的δ角可以使子图的光程差按一定的顺序等间距增加,如图 2(a)所示,图中Dopd为光程差,按此顺序排列的子图序列构成三维干涉立方体,如图 2(b)所示,经过反演可以获得光谱图像数据立方体.系统实物图如图 3所示.
|
图 2 子图间光程差关系 Figure 2 OPD of the subimages |

|
图 3 系统光路 Figure 3 Optical path diagram of our system |
传统的傅里叶成像光谱仪的反演过程主要包括干涉序列去趋势项、切趾处理、相位修正和傅里叶变换等过程,而快照式傅里叶成像光谱仪是利用一个探测器成像面获得干涉序列,所以需要经过平场处理减弱由于渐晕和透镜阵列制造误差引入的光强不均问题,然后通过精确配准,将子图阵列同名点对齐,并按光程差大小排列获得用于反演的干涉数据立方体.
2 光谱重构算法的CUDA实现随着GPU技术的迅猛发展,并行计算已经在许多领域中广泛应用.CUDA是2007年NVIDIA公司推出的通用并行架构,支持程序员利用C语言实现GPU并行编程.通过将程序中并行性较大的部分移到GPU进行计算,可以大幅度提高运行效率.
干涉数据立方体中,每个像素点的干涉序列的反演是相互独立的,像素点之间不产生影响,因此很容易将串行计算并行化:直接将每个像素点干涉序列处理分给每个线程,进行并行计算.而这需要CPU提前处理好子图阵列的平场、配准等问题,然后将提取出来的干涉数据立方体送给GPU作并行计算.
快照式傅里叶成像光谱仪一般的数据处理步骤是:先进行平场处理,然后提取出子图进行配准,最后将配准后的干涉立方体进行反演.
2.1 平场处理并行化平场过程是先将起偏器旋转90°,将仪器对准积分球出射的白光,让系统采集多幅不产生干涉的白光图像并进行平均,作为系统光强分布依据,本文称之为平场图,使用过程中,采集的目标图像除以平场图可以减小由系统原因导致的光强分布不均的影响.平场过程是作目标图像与平场图的除法,像素点之间也是互不相关的,可以在按像素点分配的并行线程中处理.
2.2 配准并行化配准的目的是让子图的同名点对齐,消除同名点之间的偏移误差,同名点偏移误差主要来源是子图提取时的中心偏移,图像畸变等原因.同相机标定类似,配准过程是将每幅子图的配准参数预先存起来,使用时直接利用参数对目标图进行校正.然而利用配准参数 (如一个仿射变换矩阵) 对子图进行校正也是一个十分消耗计算量的过程,而且比较难按像素点进行并行处理.
考虑到在正常使用时,子图的相对位置,相对畸变是固定的,也就是每个同名点在成像面的位置是固定的,利用这个特性,配准的过程可以变换为预先计算出每个同名点的坐标,直接利用坐标信息对采集的图像进行重采样即可.经过改进后的配准过程为:首先对一个棋盘格模板进行成像,提取出每个子图并进行子图间的配准 (一般采用正中间畸变小的子图作为参考图),计算出每个同名点在每个子图中的坐标,进而得到每个同名点在采集到的原图中的坐标,将坐标信息存成一个配准矩阵,该矩阵在系统搭好后由CPU生成,使用时直接根据矩阵对采集到的图像进行重采样即可获得配准后的干涉数据立方体.
这样配准过程简化了利用坐标进行重采样的过程,重采样本身是一种插值计算,插值是一种空间局部性高的计算,无论是双线性插值还是立方插值,都需要根据待计算点周围的4或8个像素点的值才能确定当前点的值.如果直接利用全局存储器进行处理,不满足合并访问条件,数据访问效率低,而GPU上的纹理内存器支持一维、二维和三维纹理,且对数据的随机访问和非对齐访问有良好的加速效果,可以有效解决数据无法合并的问题.这样,配准过程便可以直接按同名点进行并行处理:首先CPU将采集的图像传输到GPU的纹理内存,同时GPU分配给每个同名点一个线程,该线程获取CPU传输过来的坐标数据,利用坐标数据直接从纹理内存中取出坐标数据对应的干涉序列.
2.3 并行光谱反演经过平场和配准的干涉序列,每个同名像素点之间的光谱反演都是相互独立的,为每个同名像素点反演分配线程即可展开并行计算.每个像素点干涉序列的光谱反演过程包括了干涉序列去趋势项,相位校正,切趾,傅里叶变换等过程.其中去趋势项处理采取最小二乘法进行[15],基本实现过程分为3步,依次是建立趋势项模型,求解趋势项,和去除趋势项,具体求解公式为
| $ \begin{array}{c} \left[ {\begin{array}{*{20}{c}} {{b_0}}\\ {{b_1}}\\ {{b_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} N&{\sum n }&{{{\sum n }^2}}\\ {\sum n }&{{{\sum n }^2}}&{{{\sum n }^3}}\\ {{{\sum n }^2}}&{{{\sum n }^3}}&{{{\sum n }^4}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {\sum {{u_n}} }\\ {\sum {n{u_n}} }\\ {\sum {{n^2}{u_n}} } \end{array}} \right],\\ {U_n} = \sum\limits_{k = 0}^2 {{b_k}{n^k}} ,\\ {f_n} = {u_n} - {U_n}. \end{array} $ |
式中:un为均匀采样的干涉信号;Un为利用最小二乘法求得的趋势项;n为采样点数.
求解趋势项过程中涉及到多次累加计算,在CPU中计算一般采用for循环求解长度为N的序列的和,需要的计算量是N-1次. GPU中针对长度为N的数据求和问题,通常可以采用并行规约的思想,每个循环内使用目前数据元素一半的线程,求解每两个元素的和,将每次循环参加运算的线程减少一半,计算量降低至log2 N次,可以有效提高算法的处理速度.
根据傅里叶变换光谱学原理,干涉数据和光谱数据是一对基于光程差的傅里叶变换对[16],对经过预处理的数据进行傅里叶变换即可得到复原光谱.傅里叶变换对CPU而言是非常耗时的,而傅里叶变换本身是可并行的,可以在GPU中快速实验.而CUDA中提供了并行快速傅里叶变换库,包括一系列用于傅里叶计算的函数,支持用户进行一维、二维或三维傅里叶变换,且同时支持单精度浮点和双精度浮点运算.直接利用库函数可以大大提高傅里叶变换效率.
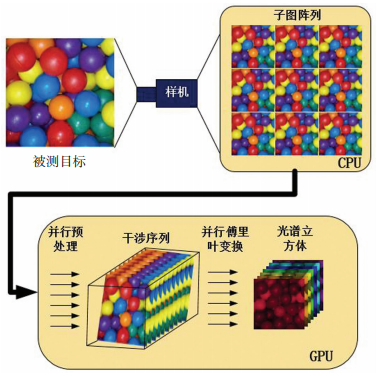
经过上述改进,对复原算法中可并行部分最大限度的并行化,并利用GPU的特性提高计算效率.而在CPU端的工作仅仅为采集数据,载入平场和配准参数,然后将采集的数据和载入的参数拷贝给GPU,通过GPU进行平场,配准等预处理获得干涉图序列,再对每个同名像素点进行反演获得光谱图像立方体,待GPU计算完之后将光谱图像数据立方体拷回CPU进行后续显示等操作,具体处理流程如图 4所示.本系统选用的GPU为Nvidia GeForce GTX 680显卡,显存容量2GB,流处理单元1 536个,核心频率1 058 MHz.
|
图 4 GPU并行化算法处理流程 Figure 4 Flow of GPU parallel algorithm processing |
在CUDA中,对数据集的操作主要可分为两部分,分别是数据传输和数据并行计算.数据传输是指:利用GPU对一数据集进行计算前,需要将数据从主机传输到设备上;在设备上完成对数据的处理后,需要将结果传输回主机,进行后续处理.
GPU中存在着多种存储器,不同种存储器之间的访问速度和访问延迟不同,需要根据数据特性选择数据存储方式和数据传输方式.通常情况下,数据一般会被复制到全局存储器,这时通常需要通过合并和对齐的方式减少访问延迟,提高数据读取效率.对需要多次访问,且只进行读操作没有写操作的数据,可以将其复制到常数存储器中,以提高访问效率.
第2节主要讨论如何将算法最大限度并行化以充分利用GPU.而处理过程中并非简单的为每个像素点各分配一个线程就可以达到最优的计算效率,本节针对计算中的存储器分配进行讨论.
3.1 页锁定存储器的分配在实际应用中,CPU需要向GPU传输大量数据,CPU预先开辟内存存储数据,然后GPU从该内存区域取走数据.主机端CPU的内存分为可分页内存和页锁定内存两种.可分页内存,基于虚拟内存技术,支持内存页的“换进换出”,可被映射到磁盘上,使得程序可以访问比实际物理内存更大的空间.页锁定内存,不参与系统的内存分页管理,因此,系统管理开销低,访问速度更快.此外,锁页内存允许GPU上的直接存储器读取DMA控制器请求主机传输而不需要CPU主机处理器的参与,传输速度更快,因此,可以通过利用页锁定存储器代替可分页存储器的方式进行程序加速.
页锁定内存的分配有两种方式,一种是将分配的可分页内存注册为页锁定内存,这种分配方式会引入额外的数据复制时间;另一种直接将普通可分页内存定义为页锁定内存.分别利用以上3种内存分配方法:(Malloc ( ) 直接分配; cudaHostAlloc ( ) 配后注册;cudaHostRegeister ( ) 接定义页锁定内存),进行一个大小为2 472×3 296的矩阵的数据传输,传输时间和传输带宽分别见表 1、2.
| 表 1 3种内存分配方法数据传输时间 Table 1 Data transmission time of three memory allocation methods |
| 表 2 3种内存分配方式数据带宽 Table 2 Data bandwidth of three memory allocation methods |
由表 1、2可知,可分页存储器的传输带宽约为2.5 GB/s,而页锁定存储器的传输带宽约为5.4 GB/s,使用页锁定内存可以有效提高数据传输带宽.但由于将分配后内存注册为页锁定内存的方式需要一个额外的数据复制时间,因此,以上3种方式中,传输效率最高的是将分页内存直接定义为页锁定内存的方式.因此,本系统采用该方式提高数据传输效率,缩短程序运行时间.
3.2 数据对齐与合并在进行并行计算时,全局存储器被大量使用,而全局存储器的读取速度慢,读取延迟长,且没有缓存机制,很容易成为程序的性能瓶颈.一般情况下CUDA从256字节对齐的地址开始数据连续访问时最有效率的,因此,在数据读取和存储时对齐有利于提高效率.此外,如果多个半线程束 (即16个线程,half-warp) 对一块连续的内存进行读写操作,击满足合并访问条件,那么多次访存操作将合并为一次,可以有效提高访问效率.
CUDA中,对显存的分配分两种,一种直接进行分配 (cudaMalloc) 但分配二维数据时,每一行的数据所占字节数不一定是256的倍数,可能会导致数据访问效率降低.另一种分配时为每一行数据多分配一些字节 (cudaMallocPitch),保证每一行数据的第一个元素都是256字节对齐的.
分别使用两种方式实现两个大小为2 472×3 296的矩阵对应元素相加的功能,程序耗时见表 3.
| 表 3 cudaMalloc与cudaMallocPitch程序耗时 Table 3 Runtime between cudaMalloc and cudaMallocPitch |
cudaMalloc内存分配方式程序平均耗时36.17 ms,cudaMallocPitch方式程序平均耗时32.29 ms,由此可见,保证数据合并与对齐,对程序具有加速效果,且当数据读取次数多时,加速效果会更明显.
3.3 共享存储器的使用去趋势项算法中将每个干涉序列设为一个线程,每个线程内利用for循环进行干涉序列提取、趋势项求解和去趋势项处理.这种方法在一定程度上,提高了程序的处理速度,原理简单,但从本质上讲,每个线程内的for循环仍然是串行处理,算法效率不高.为了获取更好的性能,应该设置更多的线程进行计算,为干涉序列中每个元素单独设置一个线程.然而,使用多个线程会引入一个问题,就是最终要计算每个元素相关项的和,为了实现这一点,线程之间必须以某种方式进行合作.共享存储器数据读取速度快,线程间可进行数据通信和同步,恰好满足以上要求,因此,可以通过使用共享存储器对去趋势项算法进行进一步的并行化加速.
4 实验结果及分析通过对程序并行化处理和对存储器优化过后,光谱重构算法将大部分计算移交给GPU,计算效率得到了提高.为测试优化后的重构算法相对于在CPU上执行的串行算法执行效率提高的程度,本文对两者的计算精度变换和执行时间作了实验比较.
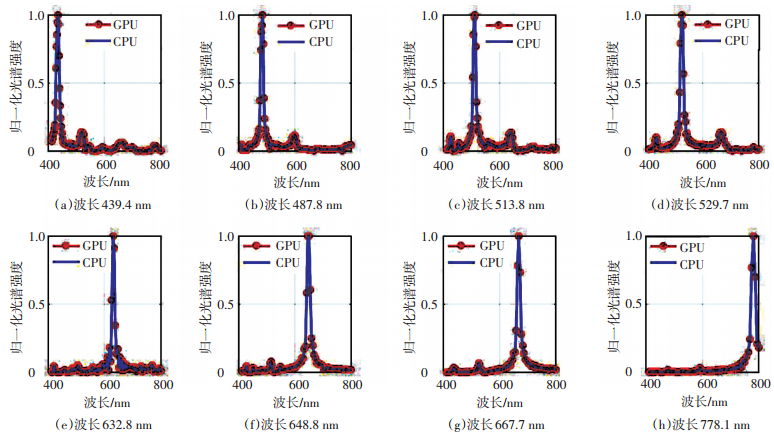
本文中采用的实验数据来自于课题组研发的快照式成像光谱仪测得的干涉数据,所得原始干涉图大小为2 472×3 296,有效干涉子图为13×18幅.采用滤光片产生波长不等的单色光,对成像光谱仪得到的干涉图分别采用CPU串行化算法和GPU并行化算法进行光谱复原.两种算法中对数据的处理方法 (包括平场,配准,去趋势项,反演) 一致,GPU并行化算法仅对CPU算法中可并行的部分移到GPU进行,其他不可并行部分仍在CPU中处理,分别对比两者的计算效率和计算精度.各不同波长单色光的复原结果如图 5所示,图中的纵坐标为归一化光谱强度.
|
图 5 不同波长光源情况下CPU与GPU算法光谱复原效果对比 Figure 5 Comparison of spectral reconstruction effects of CPU and GPU algorithms |
从图中可以看出,CPU法和GPU法的处理效果一致,采用GPU进行光谱复原,对光谱复原精度没有很大影响.两种方法的程序耗时如表 4所示,基于GPU的并行化算法的平均处理时间约为0.17 s,而传统的CPU串行化算法的平均处理时间约为4.27 s,加速比约为25.通过对程序并行化处理并借助GPU并行计算的优势,光谱重构效率得到了很大提升.
| 表 4 CPU与GPU算法程序耗时对比 Table 4 Comparison of runtime between CPU and GPU algorithms |
1) 通过分析快照式成像光谱仪的工作原理和数据特性,结合CUDA并行计算架构,将光谱重构中可进行并行处理的部分移到GPU进行,对光谱重构算法进行最大程度的并行处理,并针对并行计算中的存储器使用优化问题进行讨论,实现了基于GPU的并行化快速光谱重构算法.
2) 实验结果表明,基于GPU的并行化光谱重构算法,相对CPU串行化算法,在精度相同的情况下,计算效率提升了约25倍,利用GPU加速程序的并行部分,可以极大的提高光谱重构的效率,计算效率的高低直接影响了实时测量的效率,采用并行化算法有利于促进快照式成像光谱仪在实时测量中的应用.
| [1] | BENNETT C L, CARTER M R, FIELDS D J, et al. Imaging fourier transform spectrometer[C]// Imaging Spectrometry of the Terrestrial Environment. Orlando : Proc SPIE, 1993. DOI:10.1117/12.157065. |
| [2] | KUDENOV M W, DERENIAK E L. Compact snapshot birefringent imaging fourier transform spectrometer[J]. Proceedings of SPIE-The International Society for Optical Engineering, 2010, 7812(3): 781206-781211. DOI: 10.1117/12.945873 |
| [3] | GAO Liang, WANG L V. A review of snapshot multidimensional optical imaging: measuring photon tags in parallel[J]. Physics Reports, 2016, 616: 1-37. DOI: 10.1016/j.physrep.2015.12.004 |
| [4] | HAGEN N A, KUDENOV M W. Review of snapshot spectral imaging technologies[J]. Optical Engineering, 2013, 52(9): 72-72. DOI: 10.1117/1.OE.52.9.090901 |
| [5] | PRATX G, XING L. GPU computing in medical physics: a review[J]. Medical Physics, 2011, 38(5): 2685-2697. DOI: 10.1118/1.3578605 |
| [6] | SRIVASTAVA A.GPU accelerated variational methods for fast phononic eigenvalue solutions[C]// Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series. San Diego: Proc SPIE, 2015. DOI:10.1117/12.2083748. |
| [7] |
姚平. CUDA平台上的CPU/GPU异步计算模式[D]. 合肥: 中国科学技术大学, 2010.
YAO Ping. CPU/GPU Asynchronous computing patterns on CUDA[D]. Hefei:University of Science and Technology of China, 2010. |
| [8] | TORTI E, DANESE G, LEPORATI F, et al. Ahybrid CPU-GPU real-time hyperspectral unmixing chain[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2016, 9(2): 945-951. DOI: 10.1109/JSTARS.2015.2485399 |
| [9] | PAZ A, PLAZA A.A new morphological anomaly detection algorithm for hyperspectral images and its GPU implementation[C]// SPIE Optical Engineering + Applications. International Society for Optics and Photonics. San Diego: Proc SPIE, 2011:179-183. DOI:10.1117/12.892282. |
| [10] |
柳家福, 吴泽彬, 刘天石, 等. 基于GPU的高光谱遥感岩矿信息快速提取方法[J].
中国科技论文, 2014(10): 1137-1143.
LIU Jiafu, WU Zebin, LIU Tianshi, et al. A quick extraction method for hyperspectral remote sensing rock mineral information based on GPU[J]. China Science Paper, 2014(10): 1137-1143. DOI: 10.3969/j.issn.2095-2783.2014.10.010 |
| [11] | BERNABE S, LOPEZ S, PLAZA A, et al. GPU implementation of an automatic target detection and classification algorithm for hyperspectral image analysis[J]. Geoscience & Remote Sensing Letters IEEE, 2013, 10(2): 221-225. DOI: 10.1109/LGRS.2012.2198790 |
| [12] |
李昌国. 基于谱间和校正相关性的高光谱图像压缩方法研究及GPU并行实现[D]. 成都: 成都理工大学, 2015.
LI Changguo. Study and GPU parallel implementation of the hyperspectral image compression method based on interband and calibration correlations[D]. Chengdu:Chengdu University of Technology, 2015. |
| [13] |
杨智雄, 廖宁放, 吕航, 等. 基于CUDA的傅里叶变换成像光谱仪数据重建[J].
光学技术, 2013(2): 128-132.
YANG Zhixiong, LIAO Ningfang, LÜ Hang, et al. Fast data reconstruction method of Fourier transform imaging spectrometer based on CUDA[J]. Optical Technique, 2013(2): 128-132. |
| [14] | JIN Peng, ZHU Shuaishuai, ZHANG Yu, et al. High-SNR static fourier-transform imaging spectrometer based on differential structure[C]// Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series. San Francisco: Proc SPIE, 2015. DOI:10.1117/12.2078136. |
| [15] |
王广斌, 刘义伦, 金晓宏, 等. 基于最小二乘原理的趋势项处理及其MATLAB的实现[J].
有色设备, 2005(5): 4-8.
WANG Guangbin, LIU Yilun, JIN Xiaohong, et al. Treatment of tendency part and its MATLAB accomplishment based on least-square principle[J]. Non-Ferrous Metallurgical Equipment, 2005(5): 4-8. |
| [16] | DAVIS S P, ABRAMS M C, BRAULT J W. Fourier transform spectrometry[M]. San Diego: Academic Press, 2001. |
 2017, Vol. 49
2017, Vol. 49


