电力系统潮流计算是电网稳态分析的基础和重要工具.经过多年的研究,电力系统潮流计算技术已经相当成熟[1-5].灵敏度用于分析给定边界条件的小变化对潮流结果的影响,是潮流分析的重要手段[6-10].常规的潮流计算技术仅考虑PQ、PV、Vθ三类节点,传统的电力设备均可以建模为其中的某一类节点.然而随着电网的迅速发展,一些新型的电力设备,尤其是电力电子设备,需要使用新的节点类型刻画.另一方面,电网分析计算水平的提高也需要潮流计算具有更好的兼容性.在这一背景下,考虑其他节点类型的潮流计算技术就成为研究的热点.文献[11]提出了早期的节点类型扩展潮流计算研究,能够考虑7种节点类型.文献[12]引入PQV节点来对统一潮流控制器进行建模并进行潮流计算.文献[13]在进行潮流模型匹配计算时使用了含Qq节点的潮流计算.文献[14]在节点扩展连续潮流中引入了PQV和P节点来计算电压稳定临界点.文献[15-16]对节点类型扩展潮流计算进行了系统的研究,并提出了可解性判据,为节点类型扩展潮流计算的进一步发展打下了坚实的基础.在此基础上,文献[17]提出了基于支路功率选取的扩展潮流计算.
文献[18]根据光储置特点实现对含扩展QV节点潮流的求解了坚实的基础.灵敏度分析是潮流计算的重要扩展应用,然而当潮流计算的节点类型需要扩展时,尚缺乏有效的方法对新环境下的灵敏度系数进行分析.
本文对节点类型扩展潮流计算的灵敏度分析方法进行了研究.对常见的灵敏度因子[19],推导出了其在节点类型扩展潮流计算条件下的计算公式.基于14节点和118节点系统,比较了常规灵敏度和扩展潮流灵敏度在模拟电网潮流变化时的精度.
1 常规灵敏度计算方法电力系统潮流分析的灵敏度和分布因子种类很多.本文选取一些常用的种类,对其常规计算方法进行简要回顾[19].
1) 发电机机端电压和负荷节点电压之间的灵敏度.设全节点的PQ分解法潮流计算无功修正方程为
| $ - \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{L}}_{{\rm{DD}}}}} & {{\mathit{\boldsymbol{L}}_{{\rm{DG}}}}} \\ {{\mathit{\boldsymbol{L}}_{{\rm{GD}}}}} & {{\mathit{\boldsymbol{L}}_{{\rm{GG}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta {\mathit{\boldsymbol{U}}_{\rm{D}}}} \\ {\Delta {\mathit{\boldsymbol{U}}_{\rm{G}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\Delta {\mathit{\boldsymbol{Q}}_{\rm{D}}}} \\ {\Delta {\mathit{\boldsymbol{Q}}_{\rm{G}}}} \end{array}} \right]. $ | (1) |
其中下标G,D分别表示发电机节点和负荷节点,矩阵L为PQ分解法潮流计算中考虑全节点的无功迭代系数矩阵.
建模为PV节点发电机的机端电压UG对建模为PQ节点的负荷电压UD灵敏度的计算公式为
| $ \left\{ \begin{array}{l} \Delta {\mathit{\boldsymbol{U}}_{\rm{D}}} = {\mathit{\boldsymbol{S}}_{{\rm{DG}}}}\Delta {\mathit{\boldsymbol{U}}_{\rm{G}}}, \hfill \\ {\mathit{\boldsymbol{S}}_{{\rm{DG}}}} = - \mathit{\boldsymbol{L}}_{{\rm{DD}}}^{ - 1}{\mathit{\boldsymbol{L}}_{{\rm{DG}}}}. \hfill \\ \end{array} \right. $ | (2) |
2) 发电机无功和负荷节点电压之间的灵敏度.设式 (1) 中系数矩阵的逆矩阵为
| $ - {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{L}}_{{\rm{DD}}}}} & {{\mathit{\boldsymbol{L}}_{{\rm{DG}}}}} \\ {{\mathit{\boldsymbol{L}}_{{\rm{GD}}}}} & {{\mathit{\boldsymbol{L}}_{{\rm{GG}}}}} \end{array}} \right]^{ - 1}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_{{\rm{DD}}}}} & {{\mathit{\boldsymbol{R}}_{{\rm{DG}}}}} \\ {{\mathit{\boldsymbol{R}}_{{\rm{GD}}}}} & {{\mathit{\boldsymbol{R}}_{{\rm{GG}}}}} \end{array}} \right]. $ | (3) |
则发电机的无功QG对负荷电压UD灵敏度的计算公式为
| $ \Delta {\mathit{\boldsymbol{U}}_{\rm{D}}} = {\mathit{\boldsymbol{R}}_{{\rm{DG}}}}\Delta {\mathit{\boldsymbol{Q}}_{\rm{G}}}. $ | (4) |
3) 发电机无功和机端电压之间的灵敏度.发电机的无功QG对机端电压UG灵敏度的计算公式为
| $ \Delta {\mathit{\boldsymbol{U}}_{\rm{G}}} = {\mathit{\boldsymbol{R}}_{{\rm{GG}}}}\Delta {\mathit{\boldsymbol{Q}}_{\rm{G}}}. $ | (5) |
4) 负荷电压和变压器变比之间的灵敏度.负荷节点电压UD与变压器变比t之间的灵敏度计算公式为
| $ \left\{ \begin{array}{l} \Delta {\mathit{\boldsymbol{U}}_{\rm{D}}} = {\mathit{\boldsymbol{T}}_{{\rm{Dt}}}}\Delta \mathit{\boldsymbol{L}}t\mathit{\boldsymbol{L}}, \hfill \\ {\mathit{\boldsymbol{T}}_{{\rm{Dt}}}} = - \mathit{\boldsymbol{L}}_{{\rm{DD}}}^{ - 1}\left[ {\frac{{\partial \Delta {\mathit{\boldsymbol{Q}}_{\rm{D}}}}}{{\partial {t^{\rm{T}}}}}} \right]. \hfill \\ \end{array} \right. $ | (6) |
在节点扩展潮流计算的无功迭代中,将所有节点分为以下4类:1) Q已知,U未知;2) Q、U均未知;3) Q、U均已知;4) Q未知,U已知.全节点的无功修正方程为
| $ - \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{L'}}}_{11}}} & {{{\mathit{\boldsymbol{L'}}}_{12}}} & {{{\mathit{\boldsymbol{L'}}}_{13}}} & {{{\mathit{\boldsymbol{L'}}}_{14}}} \\ {{{\mathit{\boldsymbol{L'}}}_{21}}} & {{{\mathit{\boldsymbol{L'}}}_{22}}} & {{{\mathit{\boldsymbol{L'}}}_{23}}} & {{{\mathit{\boldsymbol{L'}}}_{24}}} \\ {{{\mathit{\boldsymbol{L'}}}_{31}}} & {{{\mathit{\boldsymbol{L'}}}_{32}}} & {{{\mathit{\boldsymbol{L'}}}_{33}}} & {{{\mathit{\boldsymbol{L'}}}_{34}}} \\ {{{\mathit{\boldsymbol{L'}}}_{41}}} & {{{\mathit{\boldsymbol{L'}}}_{42}}} & {{{\mathit{\boldsymbol{L'}}}_{43}}} & {{{\mathit{\boldsymbol{L'}}}_{44}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta {\mathit{\boldsymbol{U}}_{\rm{1}}}} \\ {\Delta {\mathit{\boldsymbol{U}}_{\rm{2}}}} \\ {\Delta {\mathit{\boldsymbol{U}}_{\rm{3}}}} \\ {\Delta {\mathit{\boldsymbol{U}}_{\rm{4}}}} \end{array}} \right]{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {\Delta {\mathit{\boldsymbol{Q}}_{\rm{1}}}} \\ {\Delta {\mathit{\boldsymbol{Q}}_{\rm{2}}}} \\ {\Delta {\mathit{\boldsymbol{Q}}_{\rm{3}}}} \\ {\Delta {\mathit{\boldsymbol{Q}}_{\rm{4}}}} \end{array}} \right]. $ | (7) |
其中下标数字表示节点所属的类别.考虑到已知量和未知量,节点类型扩展潮流计算实际求解的无功修正方程为[15]
| $ - \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{L'}}}_{11}}} & {{{\mathit{\boldsymbol{L'}}}_{12}}} \\ {{{\mathit{\boldsymbol{L'}}}_{31}}} & {{{\mathit{\boldsymbol{L'}}}_{32}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta {\mathit{\boldsymbol{U}}_{\rm{1}}}} \\ {\Delta {\mathit{\boldsymbol{U}}_{\rm{2}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\Delta {\mathit{\boldsymbol{Q}}_{\rm{1}}}} \\ {\Delta {\mathit{\boldsymbol{Q}}_{\rm{3}}}} \end{array}} \right]. $ | (8) |
以式 (7)、(8) 为基础,可推导出节点类型扩展潮流计算的灵敏度计算公式.
1) 发电机机端电压和负荷节点电压之间的灵敏度.在分析发电机机端电压和负荷节点之间的灵敏度时,发电机节点的机端电压应为给定量;发电机的机端电压给定时,其注入无功应为未知量,因此发电机节点应建模为第4类节点.而负荷节点电压应为未知量,根据无功注入是否给定,其可能是第1类节点或第2类节点.此时,式 (7) 中ΔQ1、ΔQ3、ΔU3均为0.展开式 (7) 的第1行和第3行,可以得到
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{L'}}}_{11}}\Delta {\mathit{\boldsymbol{U}}_{\rm{1}}} + {{\mathit{\boldsymbol{L'}}}_{12}}\Delta {\mathit{\boldsymbol{U}}_{\rm{2}}} + {{\mathit{\boldsymbol{L'}}}_{14}}\Delta {\mathit{\boldsymbol{U}}_{\rm{4}}} = 0, \hfill \\ {{\mathit{\boldsymbol{L'}}}_{31}}\Delta {\mathit{\boldsymbol{U}}_{\rm{1}}} + {{\mathit{\boldsymbol{L'}}}_{32}}\Delta {\mathit{\boldsymbol{U}}_{\rm{2}}} + {{\mathit{\boldsymbol{L'}}}_{34}}\Delta {\mathit{\boldsymbol{U}}_{\rm{4}}} = 0. \hfill \\ \end{array} \right. $ | (9) |
将式 (9) 整理为矩阵形式,则有
| $ \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{L'}}}_{11}}} & {{{\mathit{\boldsymbol{L'}}}_{12}}} \\ {{{\mathit{\boldsymbol{L'}}}_{31}}} & {{{\mathit{\boldsymbol{L'}}}_{32}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta {\mathit{\boldsymbol{U}}_{\rm{1}}}} \\ {\Delta {\mathit{\boldsymbol{U}}_{\rm{2}}}} \end{array}} \right] = - \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{L'}}}_{14}}} \\ {{{\mathit{\boldsymbol{L'}}}_{34}}} \end{array}} \right]\Delta {\mathit{\boldsymbol{U}}_{\rm{4}}}. $ | (10) |
设式 (10) 中系数矩阵的逆矩阵为
| $ {\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{L'}}}_{11}}} & {{{\mathit{\boldsymbol{L'}}}_{12}}} \\ {{{\mathit{\boldsymbol{L'}}}_{31}}} & {{{\mathit{\boldsymbol{L'}}}_{32}}} \end{array}} \right]^{ - 1}} = \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{R'}}}_{11}}} & {{{\mathit{\boldsymbol{R'}}}_{12}}} \\ {{{\mathit{\boldsymbol{R'}}}_{31}}} & {{{\mathit{\boldsymbol{R'}}}_{32}}} \end{array}} \right]. $ | (11) |
则由式 (10)、(11) 可以得到发电机电压与负荷电压之间的灵敏度关系为
| $ \Delta {\mathit{\boldsymbol{U}}_{\rm{1}}} = - \left( {{{\mathit{\boldsymbol{R'}}}_{11}}{{\mathit{\boldsymbol{L'}}}_{14}} + {{\mathit{\boldsymbol{R'}}}_{12}}{{\mathit{\boldsymbol{L'}}}_{34}}} \right)\Delta {\mathit{\boldsymbol{U}}_{\rm{4}}}, $ | (12) |
| $ \Delta {\mathit{\boldsymbol{U}}_{\rm{2}}} = - \left( {{{\mathit{\boldsymbol{R'}}}_{31}}{{\mathit{\boldsymbol{L'}}}_{14}} + {{\mathit{\boldsymbol{R'}}}_{32}}{{\mathit{\boldsymbol{L'}}}_{34}}} \right)\Delta {\mathit{\boldsymbol{U}}_{\rm{4}}}. $ | (13) |
如负荷的Q已知,则灵敏度用式 (12) 计算,如负荷节点的Q未知,则灵敏度用式 (13) 计算.
2) 发电机无功和负荷节点电压之间的灵敏度.当分析发电机无功的灵敏度时,发电机无功作为已知量,而机端电压作为未知量,因此发电机此时属于第1类节点.而负荷节点仍然可能是第1类或第2类节点.将第1类节点划分为发电机节点和负荷节点,则式 (8) 变为
| $ - \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{L'}}}_{{\rm{GG}}}}} & {{{\mathit{\boldsymbol{L'}}}_{{\rm{GD}}}}} & {{{\mathit{\boldsymbol{L'}}}_{{\rm{G2}}}}} \\ {{{\mathit{\boldsymbol{L'}}}_{{\rm{DG}}}}} & {{{\mathit{\boldsymbol{L'}}}_{{\rm{DD}}}}} & {{{\mathit{\boldsymbol{L'}}}_{{\rm{D2}}}}} \\ {{{\mathit{\boldsymbol{L'}}}_{{\rm{3G}}}}} & {{{\mathit{\boldsymbol{L'}}}_{{\rm{3D}}}}} & {{{\mathit{\boldsymbol{L'}}}_{{\rm{32}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta {\mathit{\boldsymbol{U}}_{\rm{G}}}} \\ {\Delta {\mathit{\boldsymbol{U}}_{\rm{D}}}} \\ {\Delta {\mathit{\boldsymbol{U}}_{\rm{2}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\Delta {\mathit{\boldsymbol{Q}}_{\rm{G}}}} \\ {\Delta {\mathit{\boldsymbol{Q}}_{\rm{D}}}} \\ {\Delta {\mathit{\boldsymbol{Q}}_{\rm{3}}}} \end{array}} \right]. $ | (14) |
设式 (14) 的系数矩阵的逆矩阵为
| $ - {\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{L'}}}_{{\rm{GG}}}}} & {{{\mathit{\boldsymbol{L'}}}_{{\rm{GD}}}}} & {{{\mathit{\boldsymbol{L'}}}_{{\rm{G2}}}}} \\ {{{\mathit{\boldsymbol{L'}}}_{{\rm{DG}}}}} & {{{\mathit{\boldsymbol{L'}}}_{{\rm{DD}}}}} & {{{\mathit{\boldsymbol{L'}}}_{{\rm{D2}}}}} \\ {{{\mathit{\boldsymbol{L'}}}_{{\rm{3G}}}}} & {{{\mathit{\boldsymbol{L'}}}_{{\rm{3D}}}}} & {{{\mathit{\boldsymbol{L'}}}_{{\rm{32}}}}} \end{array}} \right]^{ - 1}} = \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{R'}}}_{{\rm{GG}}}}} & {{{\mathit{\boldsymbol{R'}}}_{{\rm{GD}}}}} & {{{\mathit{\boldsymbol{R'}}}_{{\rm{G2}}}}} \\ {{{\mathit{\boldsymbol{R'}}}_{{\rm{DG}}}}} & {{{\mathit{\boldsymbol{R'}}}_{{\rm{DD}}}}} & {{{\mathit{\boldsymbol{R'}}}_{{\rm{D2}}}}} \\ {{{\mathit{\boldsymbol{R'}}}_{{\rm{3G}}}}} & {{{\mathit{\boldsymbol{R'}}}_{{\rm{3D}}}}} & {{{\mathit{\boldsymbol{R'}}}_{{\rm{32}}}}} \end{array}} \right]. $ | (15) |
若负荷节点的无功功率已知,其属于第1类节点,则负荷节点电压和发电机无功之间的灵敏度关系为
| $ \Delta {\mathit{\boldsymbol{U}}_{\rm{D}}} = {{\mathit{\boldsymbol{R''}}}_{{\rm{DG}}}}\Delta {\mathit{\boldsymbol{Q}}_{\rm{G}}}. $ | (16) |
若负荷节点的无功功率未知,其属于第2类节点,则负荷节点电压和发电机无功之间的灵敏度关系为
| $ \Delta {\mathit{\boldsymbol{U}}_{\rm{2}}} = {{\mathit{\boldsymbol{R''}}}_{{\rm{3G}}}}\Delta {\mathit{\boldsymbol{Q}}_{\rm{G}}}. $ | (17) |
3) 发电机无功和机端电压之间的灵敏度.由式 (14) 和式 (15) 可知,发电机无功和机端电压之间的灵敏度为
| $ \Delta {\mathit{\boldsymbol{U}}_{\rm{G}}} = {{\mathit{\boldsymbol{R''}}}_{{\rm{GG}}}}\Delta {\mathit{\boldsymbol{Q}}_{\rm{G}}}. $ | (18) |
4) 负荷电压和变压器变比之间的灵敏度.此时发电机节点仍作为PV节点处理,式 (14) 简化为
| $ - \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{L'}}}_{{\rm{DD}}}}} & {{{\mathit{\boldsymbol{L'}}}_{{\rm{D2}}}}} \\ {{{\mathit{\boldsymbol{L'}}}_{{\rm{3D}}}}} & {{{\mathit{\boldsymbol{L'}}}_{{\rm{32}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta {\mathit{\boldsymbol{U}}_{\rm{D}}}} \\ {\Delta {\mathit{\boldsymbol{U}}_{\rm{2}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\Delta {\mathit{\boldsymbol{Q}}_{\rm{D}}}} \\ {\Delta {\mathit{\boldsymbol{Q}}_{\rm{3}}}} \end{array}} \right]. $ | (19) |
设式 (19) 中系数矩阵的逆矩阵为
| $ - {\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{L'}}}_{{\rm{DD}}}}} & {{{\mathit{\boldsymbol{L'}}}_{{\rm{D2}}}}} \\ {{{\mathit{\boldsymbol{L'}}}_{{\rm{3D}}}}} & {{{\mathit{\boldsymbol{L'}}}_{{\rm{32}}}}} \end{array}} \right]^{ - 1}} = \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{R'''}}}_{{\rm{DD}}}}} & {{{\mathit{\boldsymbol{R'''}}}_{{\rm{D}}2}}} \\ {{{\mathit{\boldsymbol{R'''}}}_{3{\rm{D}}}}} & {{{\mathit{\boldsymbol{R'''}}}_{32}}} \end{array}} \right]. $ | (20) |
由于第3类节点的无功注入不变,即ΔQ3=0;若负荷节点的Q已知,则根据式 (19) 和式 (20) 可得
| $ \Delta {\mathit{\boldsymbol{U}}_{\rm{D}}} = {{\mathit{\boldsymbol{R''}}}_{{\rm{DD}}}}\Delta {\mathit{\boldsymbol{Q}}_{\rm{D}}}. $ | (21) |
则负荷节点电压对变压器变比之间的灵敏度为
| $ \left\{ \begin{array}{l} \Delta {\mathit{\boldsymbol{U}}_{\rm{D}}} = {{\mathit{\boldsymbol{T'}}}_{{\rm{Dt}}}}\Delta t, \hfill \\ {{\mathit{\boldsymbol{T'}}}_{{\rm{Dt}}}} = {{\mathit{\boldsymbol{R''}}}_{{\rm{DD}}}}\left[ {\frac{{\partial \Delta {\mathit{\boldsymbol{Q}}_{\rm{D}}}}}{{\partial {t^{\rm{T}}}}}} \right]. \hfill \\ \end{array} \right. $ | (22) |
若负荷的Q未知,则
| $ \Delta {\mathit{\boldsymbol{U}}_{\rm{2}}} = {{\mathit{\boldsymbol{R''}}}_{3D}}\Delta {\mathit{\boldsymbol{Q}}_{\rm{D}}}. $ | (23) |
负荷节点电压对变压器变比之间的灵敏度为
| $ \left\{ \begin{array}{l} \Delta {\mathit{\boldsymbol{U}}_{\rm{2}}} = {{\mathit{\boldsymbol{T''}}}_{{\rm{Dt}}}}\Delta t, \hfill \\ {{\mathit{\boldsymbol{T''}}}_{{\rm{Dt}}}} = {{\mathit{\boldsymbol{R''}}}_{{\rm{3D}}}}\left[ {\frac{{\partial \Delta {\mathit{\boldsymbol{Q}}_{\rm{D}}}}}{{\partial {t^{\rm{T}}}}}} \right]. \hfill \\ \end{array} \right. $ | (24) |
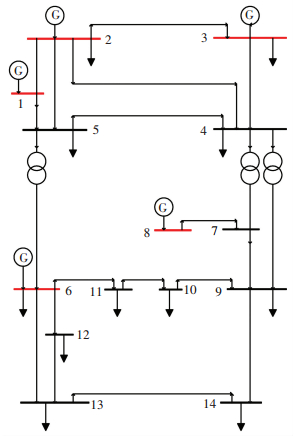
为了验证节点类型扩展潮流计算的正确性,本文首先基于IEEE 14节点系统进行算例分析, 14节点系统的结构图如图 1所示,该系统的详细数据参见文献[20].
|
图 1 IEEE 14节点系统 Figure 1 IEEE 14-bus system |
在图 1的IEEE 14节点的原始数据中,1号节点设为Vθ节点,用红色标示并连接发电机符号的节点为PV节点,其余节点为PQ节点.在此基础上,将7号节点设置为PQV节点,8号节点设置为P型节点.在本算例中,用以下3类灵敏度分析方法:1) 常规灵敏度分析法:仍保持原节点类型,用第1节所述的常规灵敏度计算公式计算灵敏度;2) 扩展潮流灵敏度分析法:用第2节所述的扩展潮流灵敏度分析方法计算灵敏度;3) 扰动法:在基态潮流解基础上附加微小扰动并分析灵敏度.为了保证扰动法的计算结果不受潮流计算收敛误差的影响,在进行扰动法计算时潮流计算的收敛门槛设置为10-10.
基于IEEE 14节点系统,分别使用传统方法和本文的节点类型扩展的灵敏度分析方法计算灵敏度因子.部分计算结果见表 1.其中,第1类灵敏度指发电机机端电压和负荷节点电压之间的灵敏度;第2类灵敏度指发电机无功功率和负荷节点电压之间的灵敏度;第3类灵敏度指发电机无功功率和机端电压之间的灵敏度;第4类灵敏度指负荷电压和变压器变比之间的灵敏度.
| 表 1 IEEE 14节点系统灵敏度分析结果 Table 1 Sensitivity factor analysis results for IEEE 14-bus system |
在表 1中,由扰动法确定的灵敏度是经过完整潮流计算得到的,最准确地体现了实际的潮流灵敏度关系.而其他两种灵敏度方法均含有线性化的近似,因此,若其结果与扰动法结果相近,则说明其精度较好.
由表 1的第4列可以看出,当潮流计算中含有新的节点类型时,仍使用传统灵敏度分析方法可能会有较大的误差,当分析对象与具有新类型的节点相关性较强时,相对误差可能超过200%.而在表 1的第5列中,本文提出的扩展潮流灵敏度分析方法的结果和扰动法接近,相对误差均在15%以下,具有较好的精度.
3.2 IEEE 118节点系统算例本文基于118节点系统同样进行了类似的算例分析,该系统的详细数据参见文献[21].在原始节点类型的基础上作如下改动:8号节点由PV节点改为P型节点,19号节点由PV节点改为0型节点,23号节点由PQ节点改为PQVθ节点,39号节点由PQ节点改为PQV节点,53号节点由PQ节点改为Pθ节点,58号节点由PV节点改为QV节点.灵敏度计算的结果如表 2所示.
| 表 2 IEEE 118节点系统灵敏度分析结果 Table 2 Sensitivity factor analysis results for IEEE 118-bus system |
通过表 2可以看出,与表 1相似,当系统中存在新的节点类型时,节点类型扩展潮流灵敏度分析结果的准确程度 (表 2的第5列) 高于传统灵敏度分析结果 (表 2的第4列).例如,对于25号节点无功与20号节点电压之间灵敏度,传统方法的计算误差超过100%,而本文提出的基于节点类型扩展潮流计算的灵敏度分析方法仅有不到1.5%的相对误差. 表 1和表 2说明了节点类型扩展潮流灵敏度分析的必要性.
3.3 实际系统算例为了验证本文提出的基于节点类型扩展潮流的灵敏度计算方法在更大规模系统的正确性,本文基于我国某省级调度中心的主网架进行算例验证.该系统共有262个节点和459条线路.在原有节点类型的基础上,设置41号节点为0型节点,189号节点为PQVθ节点,212号节点为P节点,256号节点为PQV节点.则传统灵敏度分析方法和本文方法的计算结果对比见表 3.
| 表 3 某省级实际系统灵敏度分析结果 Table 3 Sensitivity factor analysis results for provincial practical power system |
通过表 3可以看出,对于规模更大的实际系统,当系统中存在新类型节点时,如果仍然使用传统方法计算灵敏度,则会产生很大的误差,如表 3的第5列所示;而使用本文提出的节点类型扩展的灵敏度分析方法,误差会明显减小,如表 3的第7列所示.算例系统和实际系统的计算结果均表明,本文提出的节点类型扩展灵敏度分析方法是有效的.
4 结论1) 推导出了基于节点类型扩展潮流计算的灵敏度计算公式,而常规的灵敏度分析方法仅考虑PQ、PV、Vθ三类节点.
2) 算例结果表明,在潮流计算中含有新的节点类型时,常规灵敏度分析方法的准确性明显下降,而使用基于节点类型扩展潮流计算的灵敏度分析方法仍能保持很好的精度.
3) 在实际应用中,可首先分析灵敏度计算中是否涉及新的节点类型.如不涉及,则可使用传统灵敏度计算方法;否则应利用本文提出的基于节点类型扩展潮流的灵敏度计算方法.
4) 实际上,传统灵敏度分析方法可以看成是基于节点类型扩展潮流的灵敏度计算方法的一种特殊情形,随着技术的成熟,基于节点类型扩展潮流的灵敏度计算方法可以取代原有的灵敏度分析方法.
| [1] | STOTT B, ALSAC O. Fast decoupled load flow[J]. IEEE Transactions on Power Apparatus and Systems, 1974, 93(3): 859-869. |
| [2] | MONTICELLI A, GARCIA A, SAAVEDRA O R. Fast decoupled load flow: hypothesis, derivations, and testing[J]. IEEE Transactions on Power Systems, 1990, 5(4): 1425-1431. DOI: 10.1109/59.99396 |
| [3] | ZHANG X P, PETOUSSIS S G, GODFREY K R. Nonlinear interior-point optimal power flow method based on a current mismatchformulation[J]. IEE Proceedings-Generation, Transmission and Distribution, 2005, 152(6): 795-805. DOI: 10.1049/ip-gtd:20050076 |
| [4] | CHIANG H D, ZHAO T Q, DENG J J, et al. Homotopy-enhanced power flow methods for general distribution networks with distributed generators[J]. IEEE Transactions on Power Systems, 2014, 29(1): 93-100. DOI: 10.1109/TPWRS.2013.2268547 |
| [5] | SUN H, GUO Q, ZHANG B, et al. Master-slave-splitting based distributed global power flow method for integrated transmission and distribution analysis[J]. IEEE Transactions on Smart Grid, 2015, 6(3): 1484-1492. DOI: 10.1109/TSG.2014.2336810 |
| [6] | PESCHON J, PIERCY D S, TINNEY W F, et al. Sensitivity in power systems[J]. IEEE Transactions on Power Apparatus and Systems, 1968, 87(8): 1687-1696. |
| [7] | CHANG Y C, LIU C C, YANG W T. Real-time line flow calculation using a new sensitivity method[J]. Electric Power System Research, 1992, 62(24): 127-133. |
| [8] |
孙宏斌, 张伯明, 相年德. 准稳态灵敏度的分析方法[J].
中国电机工程学报, 1999, 19(4): 9-13.
SUN Hongbin, ZHANG Boming, XIANG Niande. New sensitivity analysis method under quasi-steady-state for power systems[J]. Proceedings of the CSEE, 1999, 19(4): 9-13. |
| [9] | CHEN Y C, DOMINGUEZ A D, SAUER P W. Measurement-based estimation of linear sensitivity distribution factors andapplications[J]. IEEE Transactions on Power Systems, 2014, 29(3): 1372-1382. DOI: 10.1109/TPWRS.2013.2292370 |
| [10] |
黄根, 罗滇生, 李帅虎, 等. 基于综合灵敏度分析限流的最优断线措施[J].
电网技术, 2016, 40(1): 309-315.
HUANG Gen, LUO Diansheng, LI Shuaihu, et al. Optimal line-outage measure based on comprehensive sensitivity analysis to limit short-circuit current[J]. Power System Technology, 2016, 40(1): 309-315. |
| [11] |
王鲁, 相年德, 王世缨. 广义潮流计算[J].
中国电机工程学报, 2005, 29(23): 19-24.
WANG Lu, XIANG Niande, WANG Shiying. Generalized power flow[J]. Proceedings of the CSEE, 2005, 29(23): 19-24. DOI: 10.3321/j.issn:0258-8013.2005.23.004 |
| [12] |
罗春雷, 孙洪波, 徐国禹. 含PQV节点的潮流计算在UPFC中的应用[J].
电力系统自动化, 1997, 21(4): 34-36.
LUO Chunlei, SUN Hongbo, XU Guoyu. The application of power flow calculation with PQV node for UPFC[J]. Automation of Electric Power Systems, 1997, 21(4): 34-36. |
| [13] |
蒋维勇, 吴文传, 张伯明, 等. 在线安全预警系统中的网络模型重建[J].
电力系统自动化, 2007, 31(21): 5-9.
JIANG Weiyong, WU Wenchuan, ZHANG Boming, et al. Network model reconstruction in online security early warning system[J]. Automation of Electric Power Systems, 2007, 31(21): 5-9. DOI: 10.3321/j.issn:1000-1026.2007.21.002 |
| [14] | ZHAO J, ZHOU C, CHEN G.A novel bus-type extended continuation power flow considering remote voltage control[C]//IEEE Power & Energy Society General Meeting. Vancouver: IEEE, 2013: 1-5. |
| [15] |
郭烨, 吴文传, 张伯明, 等. 节点类型扩展潮流计算的应用研究[J].
中国电机工程学报, 2011, 31(16): 81-86.
GUO Ye, WU Wenchuan, ZHANG Boming, et al. Application research on bus-type extended load flow[J]. Proceedings of the CSEE, 2011, 31(16): 81-86. |
| [16] | ZHANG Y J, YANG Y Y, LIU Z H. A joint day-ahead scheduling for photovoltaic-storage systems based on extended QV bus-type power flow[C]//International Conference on Smart Grid and Clean Energy Technologies. Offenburg: IEEE, 2015: 18-22. |
| [17] |
卢志刚, 程慧琳, 冯磊. 基于支路功率选取的功率扩展潮流计算[J].
电工技术学报, 2013, 28(6): 208-215.
LU Zhigang, CHENG Huilin, FENG Lei. Extended-power load flow calculation based on selection of branch power[J]. Transactions of China electro-technical society, 2013, 28(6): 208-215. |
| [18] |
刘泽槐, 翟世涛, 张勇军, 等. 基于扩展QV节点潮流的光储联合日前计划[J].
电网技术, 2015, 39(12): 3435-3441.
LIU Zekui, ZHAI Shitao, ZHANG Yongjun, et al. A joint day-ahead scheduling for photovoltaic-storage systems based on extended QV bus-type power flow[J]. Power System Technology, 2015, 39(12): 3435-3441. |
| [19] |
张伯明, 陈寿孙, 严正.
高等电力网络分析[M]. 2版. 北京: 清华大学出版社, 2007: 69-80.
ZHANG Boming, CHEN Shousun, YAN Zheng. Advanced electric power network analysis[M]. 2nd ed. Beijing: Tsinghua University Press, 2007: 69-80. |
| [20] | DABBAGCHI I. Power systems test case archive-14 bus power flow test case[EB/OL]. (1993-08-05)[2016-05-14]. http://www.ee.washington.edu/research/pstca/pf14/pg_tca14bus.htm. |
| [21] | CHRISTIE R. Power systems test case archive-118 bus power flow test case[EB/OL]. (1993-08-23)[2016-05-14]. http://www.ee.washington.edu/research/pstca/pf118/pg_tca118bus.htm. |
 2017, Vol. 49
2017, Vol. 49


